极端工况下螺旋槽机械密封脱开转速的理论分析和试验研究

贾 谦，阮 琪，崔 展，杨建晨，王建磊，徐鲁帅，袁小阳

（1.西安交通大学 城市学院机械工程系，西安 710018；2.中检西部检测有限公司，西安 710032；3.西安理工大学 机械与精密仪器工程学院，西安 710048；4.西安交通大学 现代设计及转子轴承系统教育部重点实验室，西安 710049）

0 引言

为实现更大的太空输送能力，火箭的重复利用成为了研究的热点。重复利用和长使用寿命一直以来是飞行器设计追求的目标，美国的Space X公司已成功进行了火箭将太空货运飞船送往国际空间站后的重复利用，我国也成功对“神箭”长征二号F运载火箭实现了重复使用［1］。在液体火箭发射过程中发动机的寿命很大程度上受涡轮泵性能的影响，所以涡轮泵设计的强健性对能否实现火箭的重复利用至关重要［2］。螺旋槽机械密封是液体火箭发动机涡轮泵的核心部件，螺旋槽机械密封的理论分析和试验技术已成为火箭发动机设计研发中的核心技术［3］。

围绕机械密封的可靠性与强健性，涌现了大量的理论和试验研究成果。在理论研究方面，李治国等［4］从模型入手，建立了考虑泄漏和传导的密封热流模型实现了对端面密封静态和动态性能的计算分析；王建磊等［5-6］针对液体火箭发动机涡轮泵机械密封磨损现象，以宏观试验与微观检测相结合的方法探索其产生机理，并且采用非接触的超声检测技术对润滑膜进行了测试；徐鲁帅等［7］从模型方面入手，关注的重点是瞬态启动过程螺旋槽机械密封性能的变化情况；张国渊等［8］研究了动静结合型机械密封的主动可控性，从原理和算法上研究了其脱开现象和泄漏量；LEBECK［9］考虑机械密封端面的波度、锥度和粗糙度，建立了机械密封泄漏模型。在试验研究方面，门川皓［10］研究了由电导探头和高速摄像机组成的两相流监测系统，并设计了能够调节的高温装置及加压装置，以研究温度及压力对密封汽液两相润滑的影响；LUO等［11］通过试验研究不同挤压故障程度下的机械密封动态特性；SHI等［12］试验研究了多种表面纹理对机械密封性能的影响；GLIENICKE等［13］对高压、高速下的螺旋槽进行了实验研究，结果表明高压、高速工况下，在密封端面形成稳定的全膜润滑以消除接触是可行的。

上述对机械密封的理论和试验研究各具特色，但缺少机械密封在启动后动、静环何时互相脱离的研究，只有动、静环脱开机械密封才能处于流体润滑状态，避免摩擦。脱开转速是衡量机械密封工作性能的一个重要参数，尤其是低黏润滑的机械密封，对脱开转速的理论和试验研究尤为重要。

1 螺旋槽机械密封脱开转速的理论研究

1.1 脱开转速的计算模型

本文研究的螺旋槽机械密封是火箭发动机涡轮泵的轴端密封，起着隔离介质和涡轮腔的作用，其结构如图1所示。由图1中可以看出，螺旋槽机械密封主要包括静环、动环和波纹管3个部分组成。静环外部为氧化剂介质，它为火箭发动机燃烧室提供燃烧所需的氧气，静环内部则为液氢、偏二甲肼等燃烧剂介质，在燃烧室内与氧化剂结合燃烧，产生使火箭升空的推力。

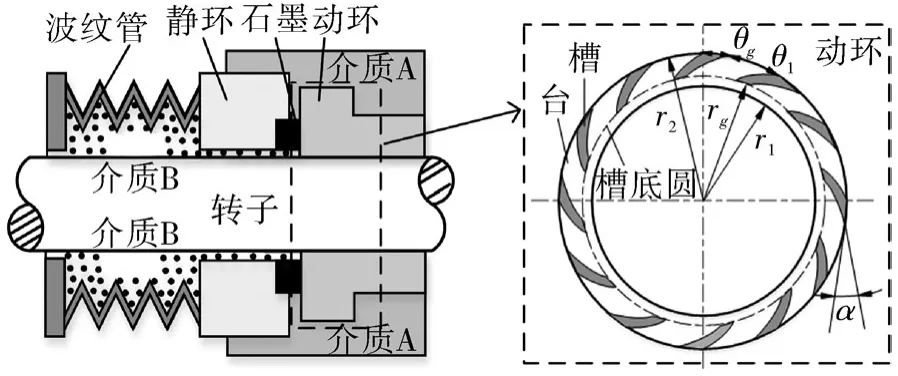
图1 螺旋槽机械密封的结构Fig.1 Structural diagram of spiral groove mechanical seals

本文关注液氮、液氧等低黏度润滑情况下的机械密封，研究其动压成膜性能。在计算中选择液氮作为密封介质，其工况和结构参数如表1所示。值得注意的是火箭发动机涡轮泵在工作时存在一个快变升速的过程，在较短时间内涡轮泵轴系的工作转速将从0升高至3×104r/min甚至更高转速。

表1 螺旋槽机械密封的工况及结构参数Tab.1 Working conditions and structural parameters of spiral groove mechanical seals

在工作的初始阶段，螺旋槽机械密封动环和静环是互相接触的，当转子升速到一定程度时动环和静环的表面会产生动压效应，导致2个环的端面分离脱开。动、静环组成的摩擦副完全脱开并形成完整润滑膜时，将依靠润滑膜进行有效的支撑，所以将动、静环相互脱开时轴系的转速称为脱开转速nt，而该转速下所对应的润滑膜厚度h可以称之为脱开膜厚ht。对于本文研究的这种螺旋槽机械密封，设计时关注的性能参数包括开启力FK、泄漏量Q、摩擦阻力矩MF和润滑膜厚h等，本文主要研究的是润滑膜厚h这一参数。采用图2所示模型对螺旋槽机械密封的润滑膜进行表达，用于进行分析的广义雷诺方程极坐标形式如式（1）所示。

图2 螺旋槽机械密封润滑膜理论分析模型Fig.2 Theoretical analysis model of lubricating film for spiral groove mechanical seals

式中 r——动、静环之间润滑介质的密度；

h——机械密封的动、静环之间的密封间隙；

μ——润滑介质的动力黏度；

p——液膜的压力；

ω——动环的转速；

V——动、静环之间的挤压速度。

取一参考平面与静环表面相重合，动环上有螺旋槽，所以需要将槽型参数代入理论分析。

动、静环平面距离为h0时动环和静环之间的膜厚h可表示为：

式中 φ——动环轴线与z轴的夹角在yz平面上的投影角；

γ——动环轴线与z轴在xz平面上的投影角；

θ——螺旋槽的起始角与z轴的夹角；

hg——螺旋槽的深度。

当动环上开有深度he的螺旋槽时，在非槽区中hg=0，在槽区中hg=he，螺旋槽机械密封润滑膜厚计算流程如图3所示。

图3 螺旋槽机械密封润滑膜厚计算流程Fig.3 Calculation flow chart of lubrication film thickness of spiral groove mechanical seals

机械密封脱开转速的判断方法有多种，最常用的是以密封端面轴向力的平衡关系作为端面是否脱开的判断依据［14-16］。在本文中螺旋槽机械密封的脱开考虑了膜厚与动、静环之间接触形貌的关系，提出完整意义上的流体润滑形成的前提是计算出的膜厚应不小于动环表面的粗糙度Ra1与静环表面的粗糙度Ra2之和，并且为了保证具有一定的安全裕度，于是添加了安全系数S后的膜厚判断如式（3）所示，式（3）也就成为判断动、静环是否实现脱开的条件［17］。

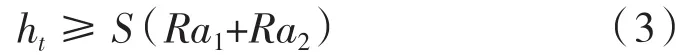
式中 ht——起飞时的润滑膜厚度；

S——安全系数；

Ra1，Ra2——动静、环表面粗糙度。

该判断方法已被成功地应用于水润滑推力轴承的相关研究中［17-20］，并且在文献［14］中已经通过实验证明了将S=1.5作为判断临界膜厚的安全系数来计算水润滑推力轴承的起飞转速时得到的膜厚结果与实际情况具有较高符合度。在本文中采用脱开膜厚与静、动环接触面的粗糙度有关作为首要判断依据，判断结果也经过了轴向平衡关系判据的验证。取S大于1，动环表面粗糙度Ra1一般为0.8 µm，静环表面粗糙度Ra2一般为1.6 µm，则根据式（3）可得脱开转速对应的润滑膜厚度为2.4 S µm，后面将通过理论分析观察在此膜厚下的转速。

1.2 脱开转速的理论分析

将表1中的工况和结构参数对螺旋槽机械密封进行了不同转速下的膜厚计算，图4示出载荷W分别为5，7.5和10 kN时，润滑膜厚h随转速n的变化，可以看出在相同W下，随着n的增加h增大，在不同载荷下，随着W的增加h减小。

图4 不同载荷下的润滑膜厚变化曲线Fig.4 Variation curve of lubricating film thickness under different loads

图4中虚线与膜厚变化曲线的交点纵坐标即为不同判断条件下的脱开膜厚值。根据式（3）当S取1.5时，ht为3.6 µm，则3个载荷下所对应的nt分别为1.0×104，1.7×104和 2.4×104r/min；当 S取 2.0时，ht为 4.8 µm，3个载荷下所对应的 nt分别为 1.7×104，2.4×104和 3.0×104r/min，W 由 5 kN提升至10 kN后，nt增加了76.5%。在上述基础之上进一步改变动环上螺旋槽的槽深hg而其它参数不变，图5示出hg分别为5，10和15 µm时膜厚随转速变化曲线。

图5 不同槽型参数下的润滑膜厚变化曲线Fig.5 Variation curve of lubricating film thickness under different groove parameters

从图5可看出，在不同hg下，随着hg的增加h越来越大，这说明较深的槽型有利于形成润滑膜。根据式（3）判据，取S=1.5时，3个槽深下所对应的 nt分别为0.2×104，0.7×104和 1.0×104r/min；取S=2.0时，3个槽深下所对应的nt分别为0.7×104，1.08×104和 1.7×104r/min。hg由 5 µm 增加到15 µm后，nt增加了143.9%。进一步改变润滑介质来进行计算，分别选取液氢、煤油和水的物性参数，图6示出不润滑介质下的润滑膜厚随转速变化曲线。从图6中可以看出，随着润滑剂黏度的增加h越来越大。

图6 不同润滑介质下的润滑膜厚变化曲线Fig.6 Variation curve of lubricating film thickness under different lubricating media

根据式（3）进行判据，当取S=1.5时，3种润滑剂所对应的 nt分别为 0.2×104，0.5×104和1.0×104r/min；当取 S=2.0时，3种润滑剂所对应的 nt分别为 0.42×104，0.8×104和 1.7×104r/min，采用水作为润滑剂时的nt分别是液氢和煤油时的4.0倍和2.1倍。

2 螺旋槽机械密封脱开转速的试验研究

2.1 脱开转速的试验方法

为进一步对脱开转速进行验证，在已有机械密封性能试验台上进行机械密封的性能测试。试验工况参数和密封结构参数见表1。如图7所示，试验台由试验腔体、驱动系统、加载系统、润滑系统与测试系统组成。采用液氮作为润滑介质，试验在温度-160 ℃时运转，轴系启动后，转子的转速从0升高至3.0×104r/min。可通过试验测量的参数包括密封介质的泄漏量Q、密封表面液膜的温度T、介质在密封入口和出口的压力差ΔP以及动环和静环之间摩擦力F，本文通过测量上述4项参数来分别研究脱开转速与该参数指标的变化关系，取最接近实际情况下的参数作为判断指标。在试验时，压力由采用安装于试验腔体中的压力传感器测量，温度采用热电偶温度传感器测量，介质泄漏量采用流量计测量，摩擦力采用扭矩传感器测量。

图7 机械密封性能试验台组成Fig.7 Composition of mechanical seal performance test bench

2.2 脱开转速试验结果分析

泄漏量Q是密封的关键指标之一，在试验中测试了转速n从0增加至3.0×104r/min这一过程中Q的变化，如图8所示。从图中泄漏流量变化趋势中可以看出，在n=2.2×104r/min时，经动环和静环之间的泄漏量Q出现了明显的增大，虽然可以说明此时端面已经形成液膜，但与图4理论分析中的1.0×104r/min比较转速偏大，因为Q主要和间隙相关，即使两面已经分开间隙可能变化不大。同样，在图8中也示出了试验中液膜温度T随转速n的变化，可以看出随着n的快速增加T升高，最高温度为-93 ℃，n=2.3×104r/min以后T趋于稳定，说明此时机械密封的液膜已经稳定。但是这个转速和理论值也差别较大，原因可能是因为温度具有累计效应，在快变升速过程中具有滞后性。可见Q和T都不能作为试验中判断脱开转速nt的依据。

图8 试验中泄漏量和温度随转速的变化Fig.8 Changes in leakage and temperature with speed during the test

机械密封进出口压力的差值ΔP是评价密封性能的重要指标，试验过程中的ΔP随转速n变化如图9所示。从图9中可以看出，随着n的升高ΔP逐渐降低，并且在1.3×104r/min以后降低地尤为显著，因此1.3×104r/min可以作为脱开转速nt的参考值，并且和理论值1.0×104r/min以及文献［15］中的试验值0.9×104r/min较为接近。

图9 试验中压差和摩擦力随转速的变化Fig.9 Change of pressure difference and friction force with speed during the test

在图9中示出了试验中F随转速n的变化曲线，可以看出在密封系统运转开始时，端面间摩擦力较大，而后随着转速的逐渐增加，端面的摩擦力随着螺旋槽产生的动压效应逐渐降低。并且可以明显看到在0.6×104～1.0×104r/min这一速度段降低尤为明显，一般来说动环材料9Cr18和静环材料石墨的干摩擦系数为0.2以上，此时摩擦系数约为0.15，说明这段转速为过渡段，介于干摩擦和边界润滑。

因此，可根据摩擦力判断nt为1.0×104r/min，这与理论分析数据吻合。上述分析表明，ΔP与F可作为试验时nt的判断依据，并且采用F判断更为精确。

3 结论

（1）引入表面粗糙度判据，即机械密封的脱开膜ht应遵循ht≥S（Ra1+Ra2），建立了nt的理论分析模型，分析了在载荷W、槽深hg及介质黏度μ等因素影响下，nt的变化规律。

（2）分析结果表明，随着转速n的增加，相同W下的h随n的增大而增大，不同载荷下的h随着W的增加而减小，不同hg下h随着hg的增加而越来越大，h随着润滑剂黏度的增大而增大。

（3）结合升速试验研究，根据试验数据表明Q、和T判断得到的nt与理论分析数据偏差较大，不宜作为判断依据，而ΔP判断得到的nt与理论分析数据相差较小，F判断得到的nt与理论分析数据吻合，可采用P和F作为试验中判断nt的依据。