基于最小化振速重构误差的等效源分布优化方法研究
2021-11-26吴绍维肖程诗王红梅
吴绍维,肖程诗,王红梅,王 艳
(1.重庆交通大学航运与船舶工程学院,重庆 400074;2.船舶动力工程技术交通运输行业重点实验室,武汉 430063)
0 引 言
边界元法(Boundary Element Method,简称BEM)是预报自由场结构声辐射最常用的方法,使用BEM 只需离散结构边界表面,且满足无穷远处的Sommerfeld 辐射条件[1]。但在常规的BEM 中,在与内部问题对应的特征频率处将出现非唯一性问题[2]。为克服此问题,Combined Helmholtz Integral Equa⁃tion Formulation(CHIEF)方法和Burton-Miller 方法是最常用的方法[1,3]。在CHIEF 方法中,当选取的CHIEF 点与结构边界为界的内部Dirichlet 问题的振型节点重合时,该方法失效[3]。Burton-Miller 法可在全频段解决此问题,但引入了格林函数各类奇异积分问题[3],这些奇异积分需进行复杂的数学处理[4-5],导致计算效率显著下降。使用有限元法(Finite Element Method,FEM)预报自由场结构声辐射面临无限域截断的问题[1,6],需采用人工边界将无限域截断为有限计算域,并在人工边界处施加无反射边界条件来代替无穷远处的Sommerfeld 辐射条件,计算域越大,消除反射声波的效果越好,但计算耗时增加,因此人工边界的选取需平衡声场预报精度和计算效率[6]。
为克服上述方法中的困难,Koopmann 等[7]提出了波叠加法(Wave Superposition Method,WSM),结构辐射的声场使用一组位于结构内部源面上的等效源辐射的声场线性叠加等效,该方法满足无穷远处的Sommerfeld 辐射条件,利用边界法向振速可求解出等效源的源强,然后通过矩阵运算即可预报任意场点处的声场量。相比于BEM 和FEM,该方法避免了奇异性问题,且无需对计算域进行截断,简化了声场预报过程。夏雪宝等[8]基于波叠加法研究了声辐射阻抗计算,分析了结构声辐射矩阵特性。钱治文等[9-10]基于波叠加法提出了一种预报浅海信道下弹性结构声辐射的联合波叠加法。但WSM 也存在不足,其预报精度受等效源分布及计算频率的影响。等效源距离结构边界较远,系统矩阵呈病态,使得方程求解不稳定而导致预报结果出现震荡;过于接近边界面时,格林函数产生近奇异性,导致错误的声场预报值。
针对等效源分布问题,国内外学者开展了众多研究。Fahnline[11]基于奇异值分解研究了波叠加法的精度和稳定性,通过对声场进行近似奇异函数展开,从物理意义上揭示了声场的本质,研究表明:波叠加法中的非唯一性是由于奇异值太小所引起,为确保预报精度,等效源应均匀分布。Hwang[12]基于虚拟声源分布提出了一种声辐射和声散射计算的正则积分方程,对一定的网格划分模式,为确保相应的积分收敛,等效源与对应的表面单元之间的距离应大于此单元的1/4特征长度。这从理论上给出了等效源距离边界面的最小距离,但仅给出下限值。若等效源距离边界太远,此时等效源之间相互距离太近,引起有关矩阵条件数增大,导致方程求解过程不稳定。Gounot[13-15]提出了一种优化确定等效源分布的遗传算法,此方法使用少量等效源,可较精确地重构简单结构辐射的声场,但该优化方法对多数量等效源失效。Zellers 及向阳等[16-17]分析了系数矩阵对角项,使用近似解析表达来替代这些对角项,但近似解析表达仅在低频率时可代替对角项。Xu等[18]提出了一种改进的波叠加法,该方法采用正则化策略,减小了系数矩阵的条件数,在一定程度上提高了计算稳定性。
针对等效源位置分布问题,本文从理论上推导了声压预报误差与振速重构误差之间的关系,揭示了两者之间的变化规律,提出了一种优化确定等效源分布的方法来提高波叠加法的声场预报精度;对于一定数量的等效源,提出了一种频率阈值准则来确定能够精确预报声场的频率范围;设计球型声源和壳型结构数值仿真对所提方法的精确性和稳定性进行了验证;最后,通过圆柱壳试验对所提方法的实用性进行验证。
1 波叠加法理论背景
波叠加法的原理是结构辐射的声场由一组位于结构内部辅助源面上的点声源叠加等效表达,这些点声源称之为等效源。结构向外部场点r处辐射的声压表示为[7]

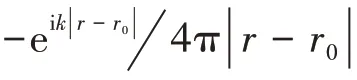
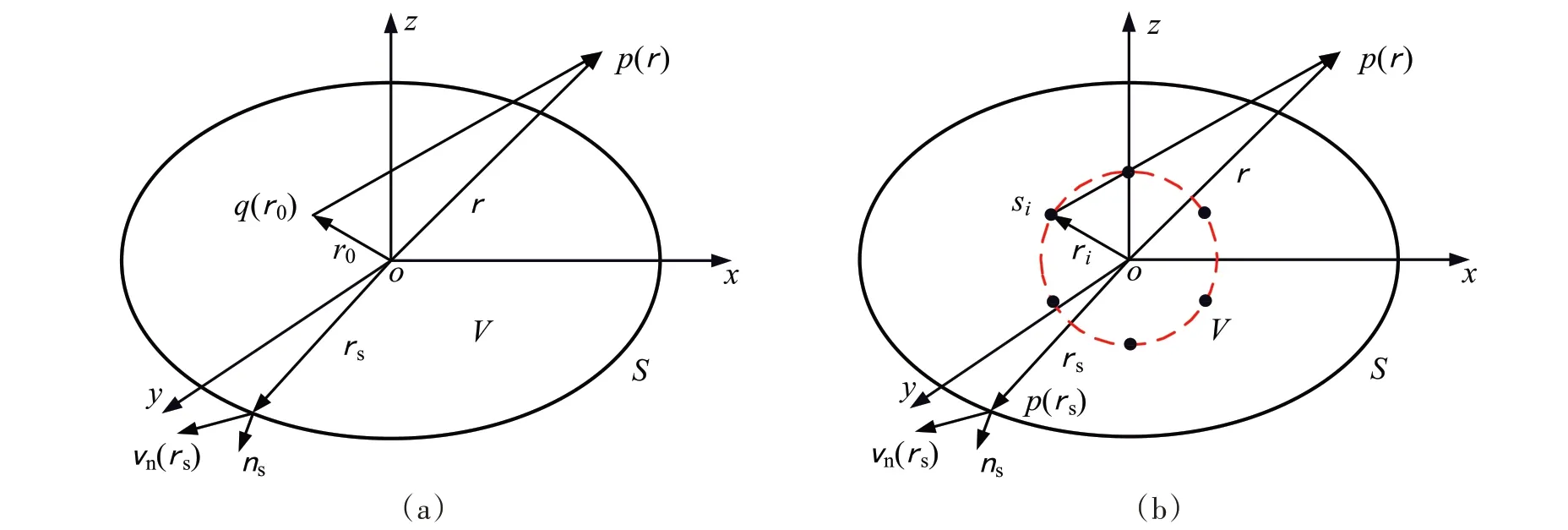
图1 波叠加法及等效源分布示意图Fig.1 Diagram of the wave superposition method and equivalent source array
通常将分布声源置于结构内部的一虚拟球壳面上,经离散化处理及代数运算,式(1)可表示为[7]


式中,∇表示关于边界面上场点rs的梯度算子,ns为场点rs处的单位外法向,v(rs)为rs处的法向速度。将式(2)代入式(3)并将其运用于边界上的N个节点,即可求解出等效源的源强,并将其代入式(2),则结构外部任意场点处的声压为

式中,v(rsj)为第j个边界节点处的法向速度,Dij为

2 等效源分布优化
2.1 振速重构误差
由式(3)可知,边界处的声压与振速并非独立,根据式(3)和式(4),边界上任意点rs处的法向振速可表示为
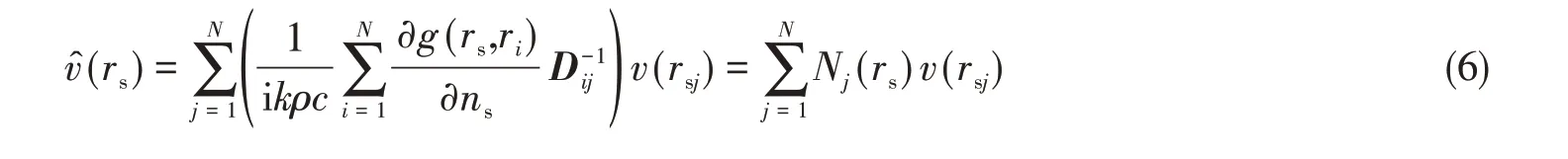
式中,Nj(rs)为速度插值函数。当rs=rsh(rsh为第h个边界节点坐标位置),Nj(rsh)如下式所示:

质量守恒方程的线性形式和状态方程为

将式(8)代入式(10)得到:

由上式可知,εp(rs)满足Helmholtz方程。式(8)可改写为

从而εp(rs)与εv(rs)满足自由场声辐射形式的结构边界条件。由于p(r)和p̂(r)均满足Sommerfeld 辐射条件,从而在无穷远处εp(rs)满足:

式中,r表示柱或球坐标中的极径,α为空间维数常数。式(13)表明,在无穷远处,εp(r)满足Sommerfeld形式的辐射条件。
式(11)~(13)与声压在无限域自由场满足的控制方程和边界条件形式一致,类比结构振动向外辐射声压,边界上的振速重构误差产生声压预报误差。抑制边界振速可降低向外辐射的声压,类比可知,减小εv(rs)能降低εp(rs),从而εv(rs)可用来反映声压预报的精度,通过最小化振速重构误差可优化确定等效源位置。在WSM 中,采用单极子型等效源在特征频率处会产生非唯一性问题,此特征频率与等效源的位置有关。当声压出现非唯一性时,振速重构误差急剧增加。因此,对于给定的频率,在确定的等效源优化位置处可避免非唯一性问题。
2.2 等效源分布优化确定
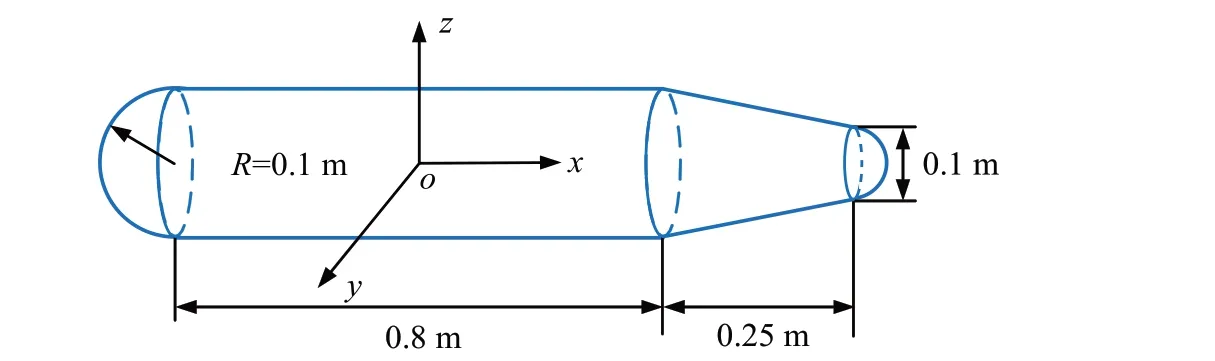
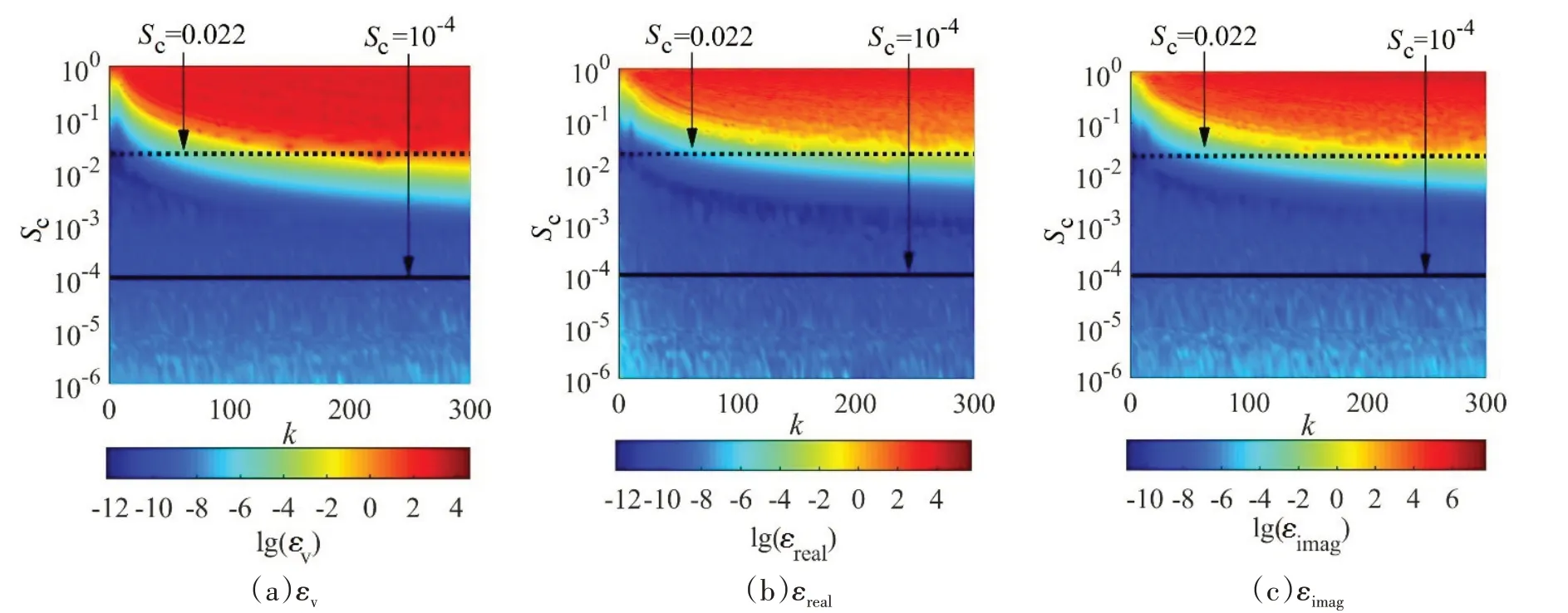
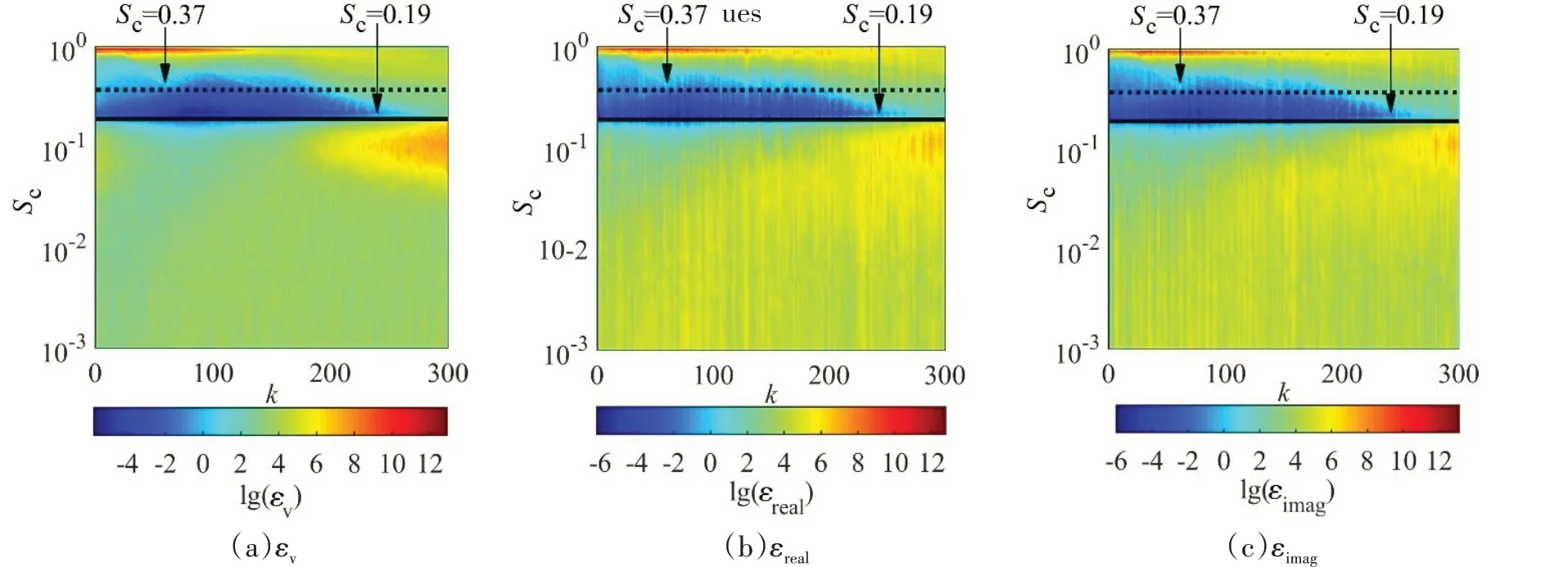
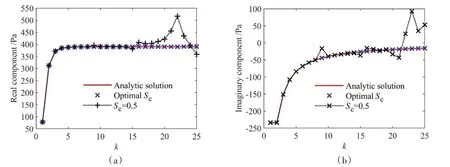
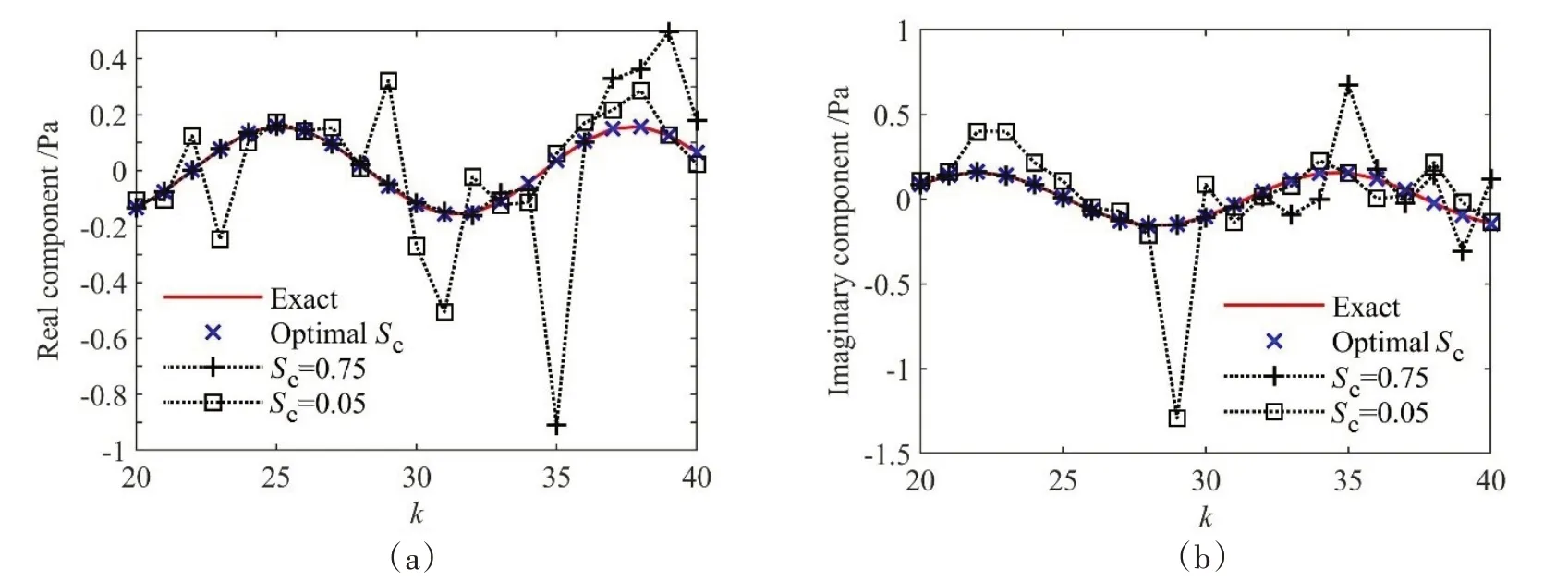
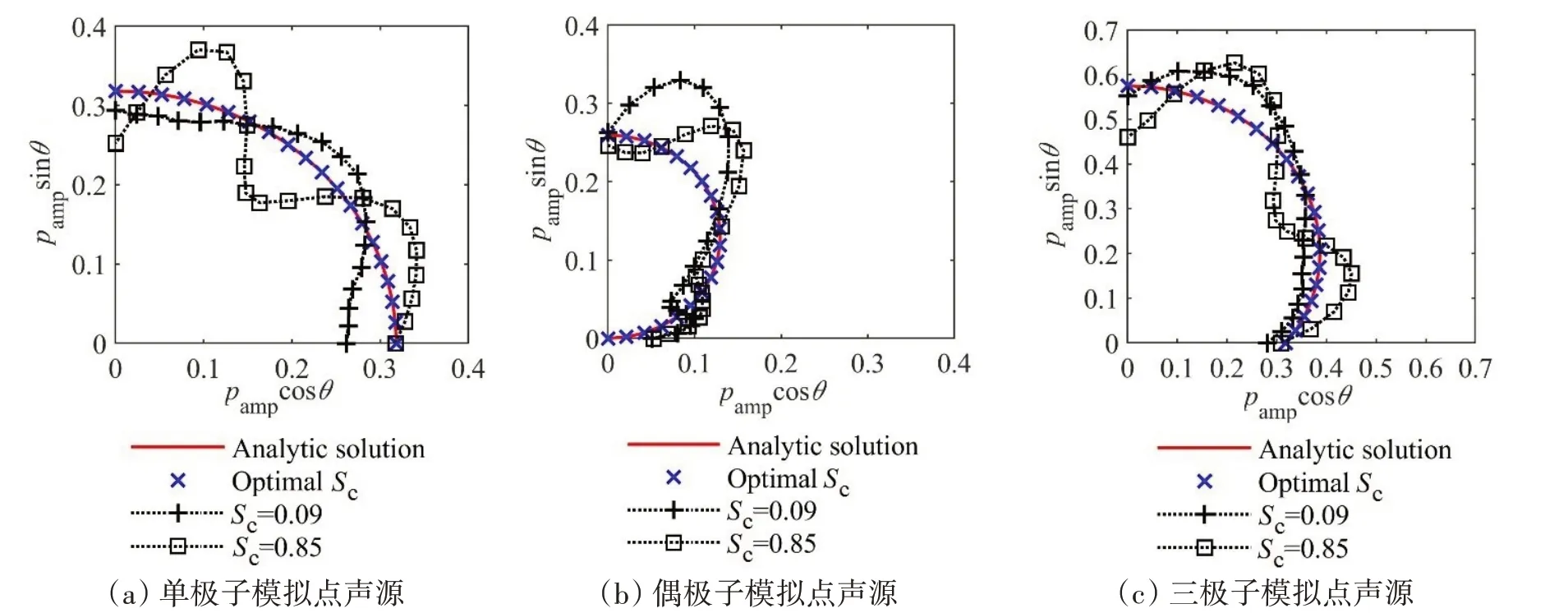
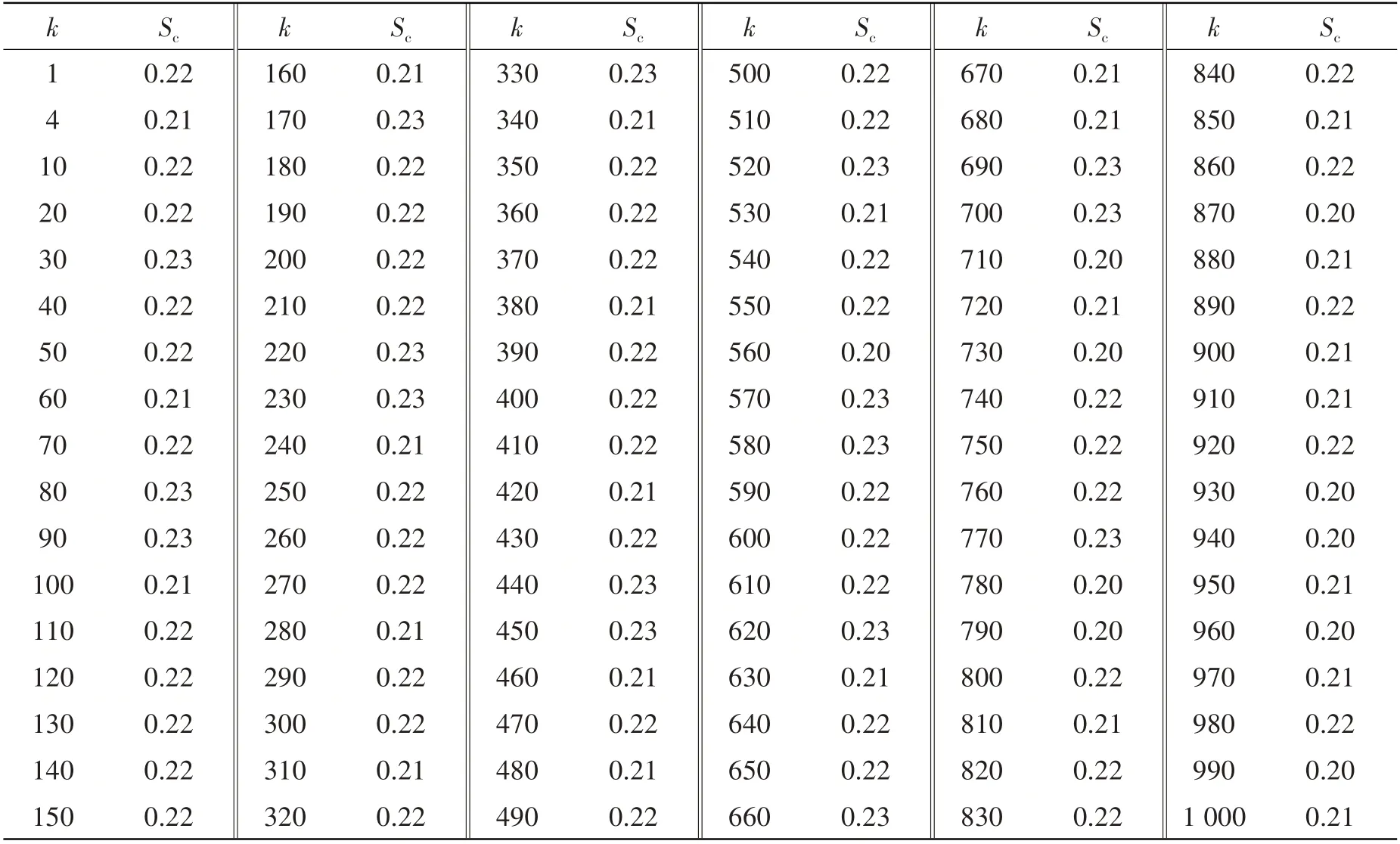
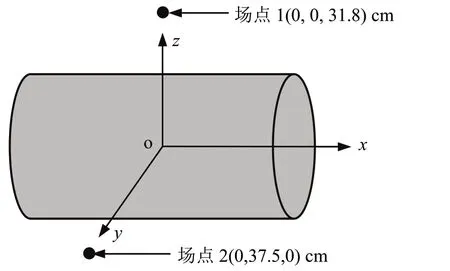
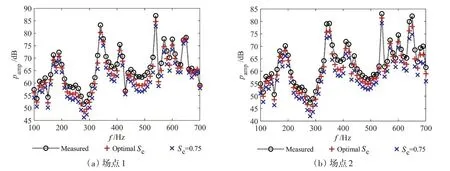
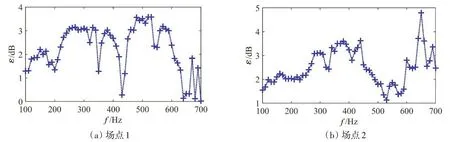
为精确预报声压,偶极矩阵D应是对角占优的。这就需对等效源和边界节点配对,使得每个等效源与所配对的节点之间的距离小于此等效源与其他节点的距离。但是,只有球形类结构以及无限长圆柱类结构满足此条件。为减少确定等效源位置分布的优化参数数量,同时使等效源源面与结构边界共形,采用缩比系数Sc(0 采用两种离散模式A 和B 离散边界,由于εv(rs)为矢量,为量化振速重构误差,定义一种无量纲振速重构误差,其解析和数值形式如下: 式中,Sj为离散模式B 下第j个节点所占区域。采用缩比系数Sc乘离散模式A 下的节点来获取等效源的空间坐标,确保等效源源面与结构表面共形,同时使用离散模式A下的节点法向振速求解等效源源强和计算声压。为优化确定Sc值,设计目标函数为 计算步骤为:对计算频率k,以离散模式A和B下的节点振速为输入,Sc以选定的步长ΔSc遍历(0,1),对每个Sc值,将离散模式A 下的节点给定法向振速代入式(6)计算离散模式B 下的节点重构法向振速v̂(rsj),将重构法向振速与离散模式B 下的节点给定法向振速代入式(14)计算无量纲振速重构误差εv;Sc遍历(0,1)之后,搜索最小εv,其对应的Sc值为最优Sc值,即可确定等效源的最优位置。 声波波长随频率的升高而减小,对一定数量的等效源,能精确预报声场的频率阈值是有限的,超过此频率阈值,预报精度急剧下降,此阈值还随辅助源面的位置改变而变化。因此,在确定等效源分布后需确定频率阈值,以确保声场预报精度可接受。 结构向外辐射的声压可表示为[7] 式中,σ表示优化确定的辅助源面,δτ为厚度常数。采用四节点或三节点单元或两种单元的任意组合离散σ,从而σ上的积分可表示为这组单元上的积分之和。空间坐标和声场变量可采用单元形函数插值近似表示,采用合适的高斯积分方法可计算单元上的积分。运用等参单元变换,全局坐标rσ和声源分布强度q(rσ)可表示为 式中,Nh为已知单元形函数,rh为单元节点全局坐标,qh为声源分布强度在节点上的值,M为单元节点数。从而式(16)可表示为 式中,K为单元数,Hih(r)可表示为 在局部坐标系s-t中,对四节点或三节点单元,式(19)分别等效表示为 式中,J(s,t)为单元映射Jacobian行列式。 对四节点单元,高斯求积的误差上限值为[12] 式中,m和n分别为s和v方向的高斯积分点数,wl和wj分别为与积分点sl和tj对应的加权因子,E1和E2为估计误差。在式(19)中的被积函数中,最主要的变化项可归纳为e-ikr/rp这种形式,其中p=1或2。因此,式(19)可近似表示为 由于被积函数中的Jacobian行列式和场点与单元之间的距离几乎是不变的,E1和E2可表示为[12] 式中,L1= max(L12,L34),L2= max(L23,L41),rmin为场点与单元之间的最小距离。为确保高斯积分收敛,k< min(4/L1,4/L2)。对三节点单元,同理可得k< min(4/L12,4/L23,4/L31)。令Lmax表示辅助源面上所有单元最大特征长度,为确保声场预报精度,k应满足 采用摆动球源(一阶球源,半径a=1,以幅值v=1 m/s 沿z轴横向振动,坐标原点位于球心)和壳型结构(如图2 所示)进行数值仿真,离散模式A 和B 下的单元类型及数量如表1 所示,其中,空气的密度ρ=1.21 kg/m3,声速c=343 m/s。 图2 壳型结构几何外形及尺寸Fig.2 Shape and size of the shell structure 表1 离散模式A与B单元类型及数量Tab.1 Number of elements on the boundary for Modes A and B 其辐射的声压解析解为 式中,θ为球面法线方向与z轴的夹角。采用如下范数作为误差指标: 式中,ε1m(%)和ε2m(%)分别为在场节点xm处预报的声压实部和虚部相对误差。 壳型结构无声压解析解,但可获取某些振速分布条件下辐射的声压准确值。在场空间中用虚拟结构封闭包裹一点声源,此点声源使在虚拟结构边界处的声介质振动,根据式(3)可计算出声介质沿边界外法向方向的振速,若结构按此振速分布向外辐射声场,则结构辐射的声场应与点声源的声场一致。因此,该点声源辐射的声场可作为对比标准,此点声源称为模拟点声源。 为研究等效源分布对声场预报精度的影响规律,图3 和图4 分别给出两种模型的εv、边界节点上的εreal和εimag随k和Sc的变化,其中壳型结构仿真采用单极子点声源作为模拟点声源,其空间坐标为(0.15 m,0 m,0 m)。 图3 摆动球源边界节点处预报误差随k与Sc的变化Fig.3 Prediction error on boundary surface of the transversely-oscillating sphere for different k and Sc val⁃ 图4 壳型结构边界节点处预报误差随k与Sc的变化Fig.4 Prediction error of εv,εreal and εimag on boundary surface of the shell structure for different k and Sc values 由图3 和图4 可知,等效源分布对声场预报精度影响显著,声场预报误差随Sc变化而改变。结果表明:εv、εreal和εimag具有相同的变化规律,εv很好地反映了声压预报误差的变化趋势;声压预报精度随εv的减小而提高,在εv取最小值的等效源分布处预报的声场精度较其他位置处高。对比图3和图4可发现,随着结构外形趋于复杂,声场预报精度对等效源位置分布变得更为敏感。对摆动球源模型,为使声压预报误差小于1%且保证方程求解过程稳定,Sc需满足0 图5 摆动球源在场节点处辐射声压随k的变化Fig.5 Variation of pressure in the selected field point with k for uniformly-pulsating sphere 图6 壳型结构在场节点处辐射声压随k的变化Fig.6 Variation of pressure in the selected field point with k for the shell structure 图中曲线显示,等效源位于优化分布位置预报的声压与准确值吻合良好,声压预报精度显著提高。结果也再次表明:结构外形越复杂,等效源分布对声场预报精度的影响越明显。因此,必须优化确定等效源分布来减小声场预报误差。根据数据分析,对摆动球源和壳型结构,等效源位于优化位置预报的声压最大误差值分别为3.7 × 10-8%和5.6 × 10-3%,优化确定的Sc值见表2。由表2 数据可知:对不同的结构,优化确定的Sc值不同;即使对同一结构,Sc值随频率的改变也存在一定的波动。 表2 不同计算频率下优化确定的Sc值Tab.2 Optimal values of Sc determined by the proposed method for different frequencies 为进一步验证所提等效源分布优化方法,对壳型结构分别采用单极子、偶极子和三极子模拟点声源进行仿真(偶极子与三极子表达式见式(29),其中→n表示偶极方向单位向量)。图7为等效源位于不同位置预报的y-z平面第一象限、半径r=0.2 m 场点处的声压幅值,其中k=20,图中pamp表示声压幅值。由结果可知,相比于其他位置,等效源处于优化位置预报的数值解与准确值吻合良好,误差得以有效抑制。 图7 壳型结构声压幅值对比Fig.7 Comparison of sound pressure amplitudes for the shell structure 对一定数量的等效源,等效源位于优化分布位置处预报的声场只在一定频率范围内具有较好的精度,超过对应的频率阈值kthreshold,误差将急剧增加。为验证所提频率阈值准则,图8为等效源位于优化位置时结构边界场点处的εreal和εimag随k的变化图,对摆动球源和壳型结构两种模型优化确定的Sc值被列于表3 和表4 中,其中壳型结构采用单极子型模拟点声源。由图中曲线可知,当计算频率超过一定值之后,声场预报精度急剧下降。对摆动球源,kthreshold值以及k 表3 摆动球源在不同计算频率下优化确定的Sc值Tab.3 Optimal values of Sc corresponding to different frequencies for uniformly-pulsating sphere 表4 壳型结构在不同计算频率下优化确定的Sc值Tab.4 Optimal values of Sc corresponding to different frequencies for shell structure 图8 等效源位于优化位置时边界场点处的εreall和εimag随k的变化Fig.8 εreal and εimag on boundary field nodes calculated in optimal auxiliary surfaces for different k 为验证提出的方法,设计了钢制圆柱壳自由场声辐射试验(见图9),该试验是通过测量获取的结构表面振速来计算结构辐射的声压,与试验测量的声压值进行对比。试验采用扬声器作为声激励源,其在圆柱壳内部产生的声场作用于圆柱壳内表面,引起圆柱壳振动向外辐射声场,结构与扬声器见图9(a)和(b),结构尺寸及材料物理属性见表5,关于试验结构的安装、固定以及密封详见文献[19-20]。将圆柱壳外表面划分为30个均匀分布的四节点单元,使用单元节点乘缩比系数Sc来获取等效源坐标,节点上的法向振速用来求解声源强度和计算声压。计算步骤为:对计算频率f,以单元节点和单元中心处的实测振速为输入,Sc以选定的步长ΔSc遍历(0,1),对每个Sc值,将单元节点处的测量法向振速代入式(6)计算单元中心处的节点重构法向振速v̂(rsj),将重构法向振速与单元节点处的测量法向振速代入式(14)计算无量纲振速重构误差εv;Sc遍历(0,1)之后,搜索最小εv并确定其对应的Sc值,Sc值对应的等效源位置即为最优位置。 图9 钢制圆柱壳自由场声辐射试验图Fig.9 Test diagram of free field acoustic radiation of steel cylindrical shell 表5 钢制圆柱壳结构物理参数Tab.5 Physical data of the steel cylindrical shell 输入扬声器的正弦信号的初始电压和电流为15 V 和1.6 A,频段为100~700 Hz,步长为Δf=10 Hz,在改变频率时保持电压恒定。逐点测量单元节点和中心处的法向加速度,根据加速度与速度的转换关系来获取这些测量点处的速度,其中使用的加速度传感器与圆柱壳的质量比为0.14%,从而可忽略传感器质量对结构振动的影响。测量如图10所示的场点声压(声传感器已采用B&K 4231 声学校准仪校准),现场声压采集如图9(c)所示,试验所使用的仪器详见文献[19-20]。 图10 目标场点坐标Fig.10 Coordinates of target field points 图11给出目标场点处的声压计算值和测量值的声压级曲线,图中pamp表示声压幅值。采用式(30)计算声压级误差: 图11 钢制圆柱壳声压幅值测量值与计算值Fig.11 Amplitude of the acoustic pressure of the cylindrical shell at selected field points 式中,pnumericalamp和pmeasuredamp分别表示声压幅值计算值和测量值,pref表示参考值。图12给出等效源位于优化位置时声压预报误差随频率的变化,表6所示为声压预报误差统计。 表6 等效源位于优化分布位置时的声压预报误差Tab.6 Prediction error in optimal auxiliary surface 图12 等效源位于优化分布位置时预报误差随频率的变化Fig.12 Variation of prediction error in optimal auxiliary surface with k 图11中的曲线表明:在采用所提方法确定的等效源优化分布位置处预报的声压幅值数值解与测量值吻合较好,对比Sc=0.75 位置处,具有更高的声场预报精度。由表6 可知,最大误差为4.79 dB,平均误差控制在2.88 dB 范围内。结果表明:在少数频点处预报的声压幅值与测量值存在一定的偏离,但平均声压预报误差仍可接受。导致最大误差偏大的主要原因是:在测量边界振速时,将所有加速度传感器底座固定在结构表面各节点处,改变了结构表面几何外形,而预报声场时未考虑这种改变。除此之外,结构周围的吸声材料未能完全吸收声波,地面仍有小部分未能铺设吸声材料,存在少量的反射声波,这些也导致声压预报值与测量值具有一定的偏离。 本文推导确定了声场预报误差与振速重构误差之间的理论关系,声场预报误差可用法向振速重构误差的变化来反映,减小振速重构误差可提高声场预报精度,通过推导确定了等效源位于优化分布位置能够精确预报声场的频率阈值。仿真结果表明:声场预报误差与法向振速重构误差的变化规律一致,相比其他固定分布位置,等效源位于优化分布位置处时,声场预报精度显著提高;频率阈值准则能够给出精确预报声场的上限频率,确保声场预报精度。试验结果表明,提出的等效源分布优化方法能有效降低声场预报误差,可用于实际声场计算。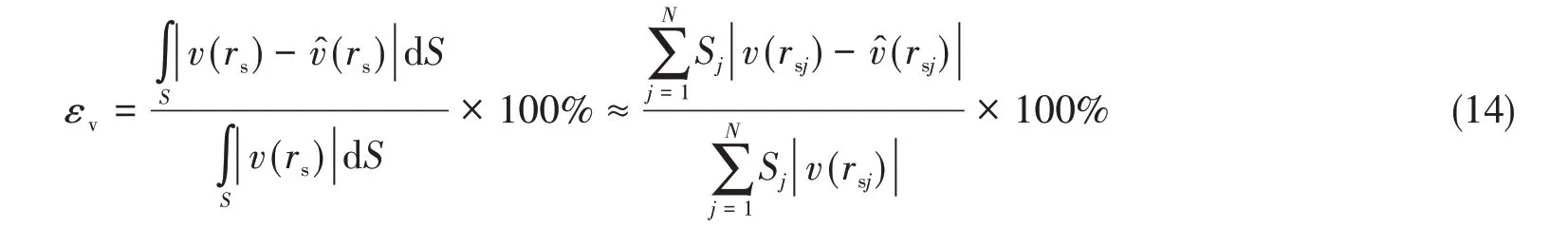
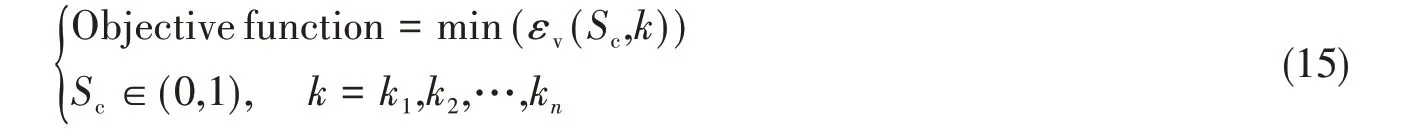
2.3 频率阈值准则
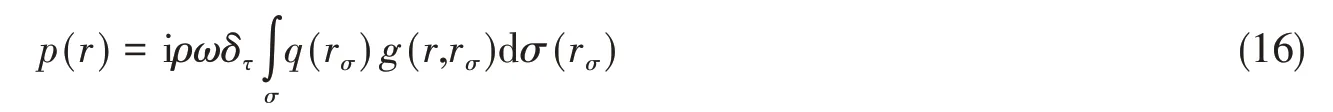



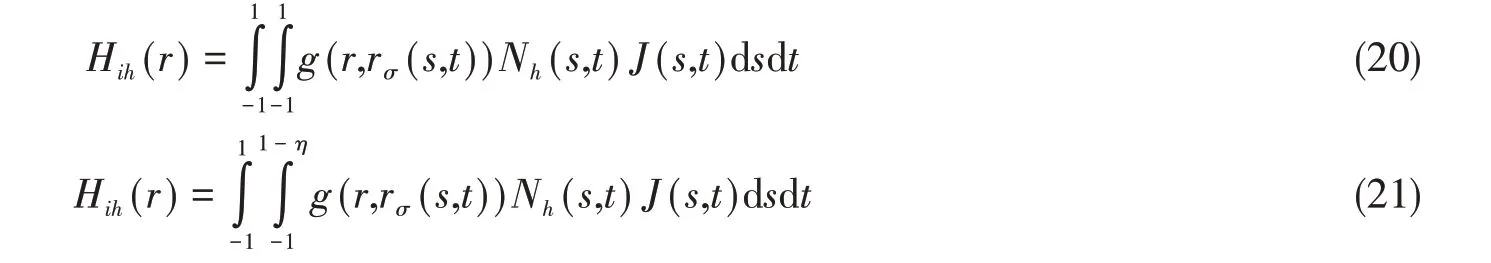
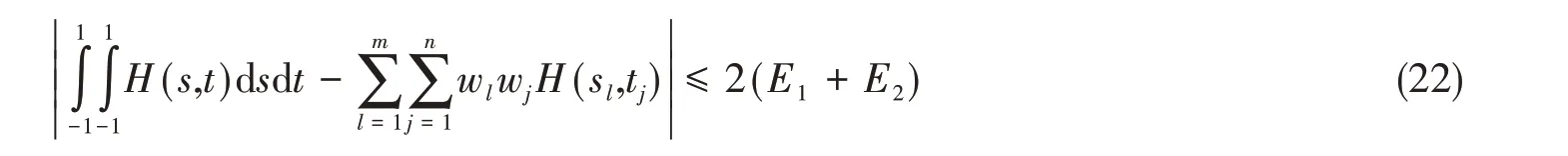

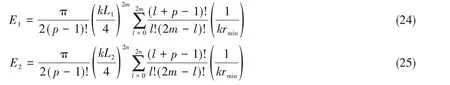

3 数值仿真
3.1 等效源分布优化方法验证

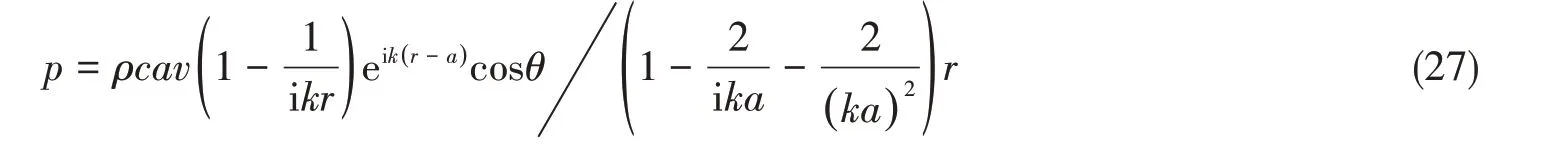
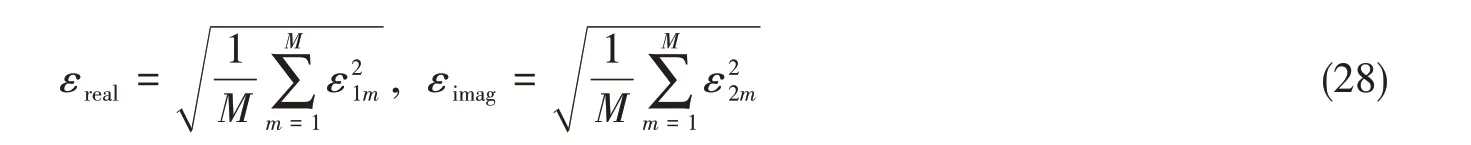
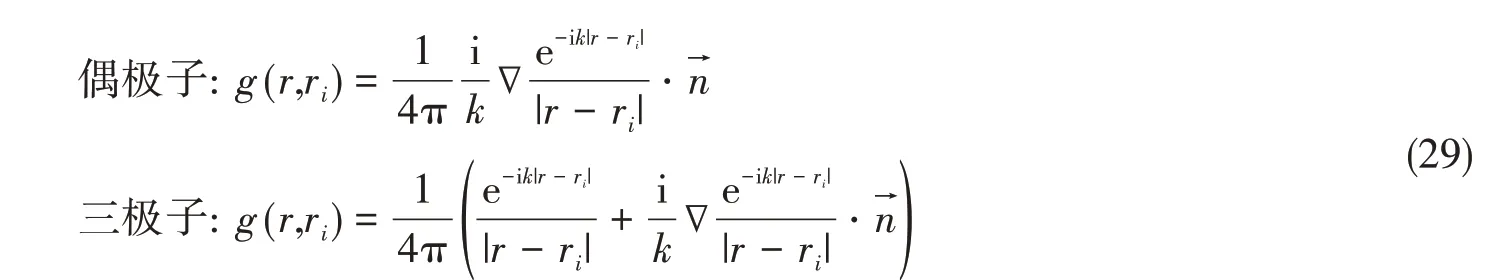
3.2 频率阈值准则验证
4 试验验证


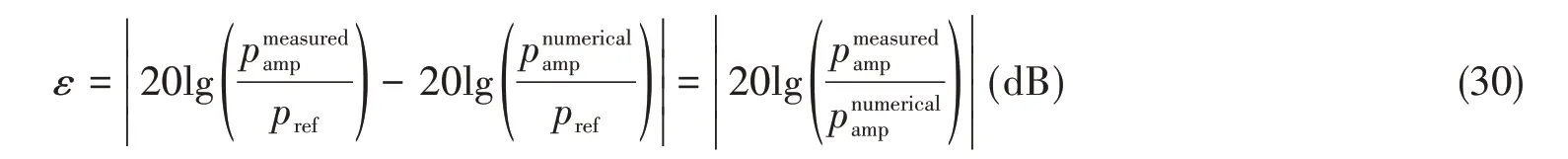

5 结 语
