一种基于板架模型的三体船连接桥结构瞬态砰击响应的分析方法
2021-11-26陈占阳杨青颖桂洪斌丛培文
陈占阳,杨青颖,于 东,桂洪斌,丛培文
(1.哈尔滨工业大学(威海),山东威海 264209;2.大连理工大学海岸和近海工程国家重点实验室,辽宁大连 116024)
0 引 言
三体船研究一直是我国船海科研领域的重中之重。由于三体船优良的性能以及主要战术性能方面的诸多优势,使其在军用、民用市场都具有广阔的应用前景[1]。2012年工信部发布的高技术船舶科研计划更是将三体船水动力性能预报技术列为八项重点基础共性技术之一。砰击破坏一直是船体结构的主要破坏形式。发生砰击时,砰击压力在结构表面的时间、空间分布特性,与入水速度、结构几何表面、结构的弹性效应等诸多因素有关。特别是三体船存在不同于单体船的片体和连接桥结构,这使得其砰击过程更为复杂。
对于三体船而言,连接桥与片体结构强度较弱,受力和变形也较为严重。许多船级社都提出应该对这部分结构进行局部的砰击加强。但究竟加强到何种程度才能保证船体具有足够的砰击强度,目前,各船级社尚未给出一致的处理意见。近年来,仅有少数文献报道了关于三体船砰击载荷及结构响应方面的研究[2-4],而相应的规范和标准中,也仅有英国劳氏船级社出版了三体船规范[5]。
此外,由于船体表面各区域位置的砰击压力并非同时达到峰值,最为合理的方法是对全船模型进行砰击载荷作用下的动力分析。但在砰击强度评估时,更主要关注局部构件的应力响应,通常需要采用细网格进行局部构件的模拟,这将导致动力分析方法需要很大的计算量。为提高计算方法的工程适用性,工程上更多的是借助等效静力系数进行静力方法评估[6-7]。但对于三体船等效静力系数的取值,目前尚没有一个明确处理方法。
综上所述,由于三体船独特的船体结构特征,使得其具有阻力小、耐波性好和稳性高等优势的同时,也导致了其载荷形式与船体结构响应不同于常规单体船,从而提高了三体船设计开发的难度[8]。因此,如何借助等效静力系数的方法对三体船局部结构的瞬态砰击响应进行分析,为结构设计提供强度依据是十分有必要的。
1 简化模型的引入
连接桥结构在砰击载荷作用下斜倾角变化较小,在进行计算分析时通常不考虑斜倾角的变化,为简化计算,板架模型就常常作为简化模型对连接桥结构进行研究。而本文主要考虑砰击载荷下的结构响应作用,因此将受砰击载荷的连接桥结构简化为板架结构。三体船分段模型及简化模型结构形式、载荷施加区域以及选取的高应力测点如图1 所示。该板架结构形状与连接桥局部结构内部结构基本一致,由外板、纵骨、纵桁和横框架构成。
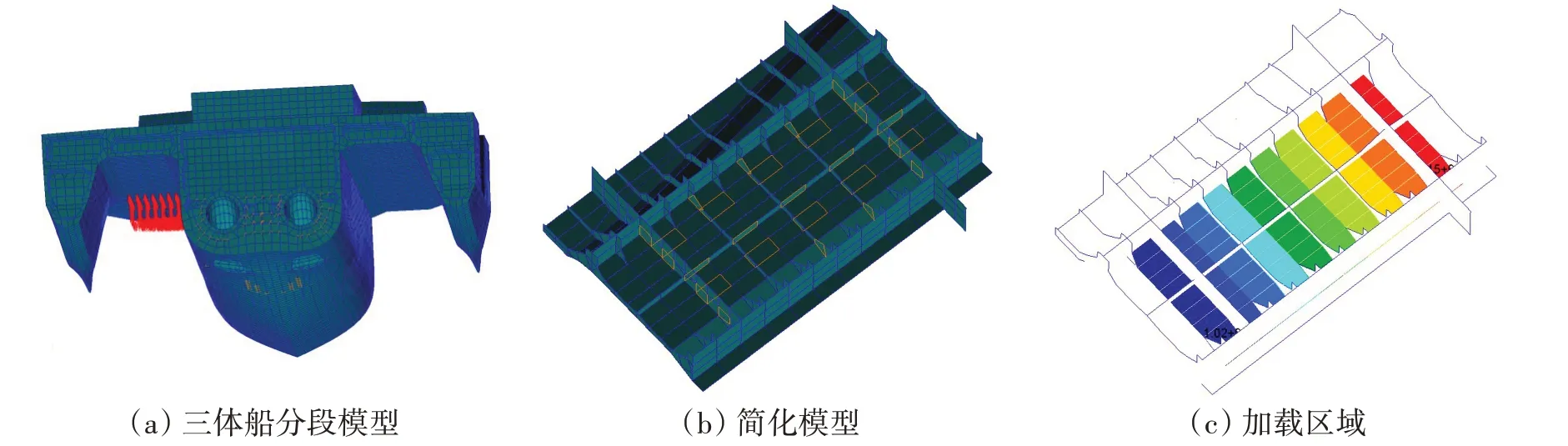
图1 模型及其加载区域Fig.1 Model and loading area
2 瞬态响应分析
通常情况下,如船舶等大型结构物在航行过程中,特别在经历复杂海况时,很容易受到波浪激励、砰击等载荷的作用。由于此类载荷作用的持续时长较短,并且快于结构的响应,这也就使得冲击结束后结构持续自由振动甚至能达到其峰值响应[9],如果采用准静态分析计算响应可能会产生较大的误差,而采取瞬态响应分析更能反应实际结果。因此,本文将模态法和直接积分法瞬态响应分析进行比较分析,并选取合适的方法进行瞬态分析。
2.1 直接法瞬态响应分析
2.1.1 直接积分法理论结构的动响应通常满足公式(1),其中P为载荷向量,u为结构动响应。
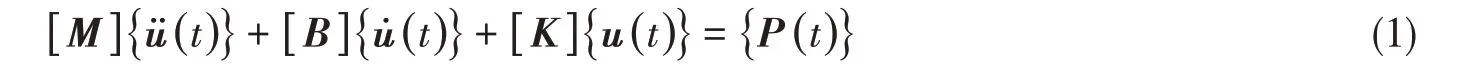
本文采用中心差分法原理进行分析,中心差分法是对动态响应使用Taylor展开,忽略高于二阶的高阶项,得
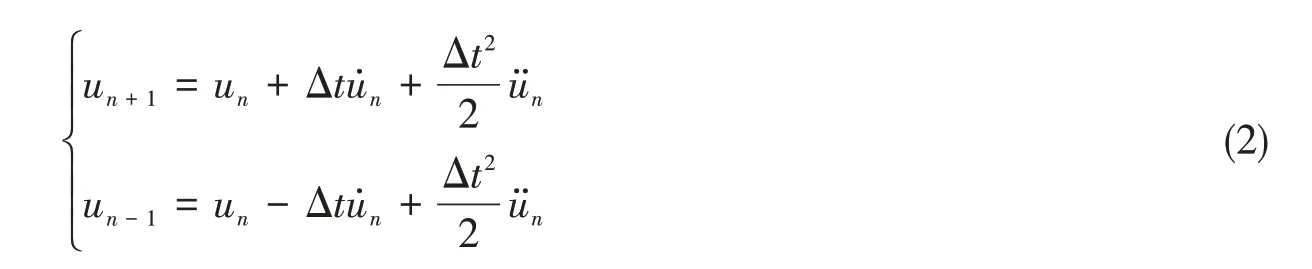
两式相加减,得
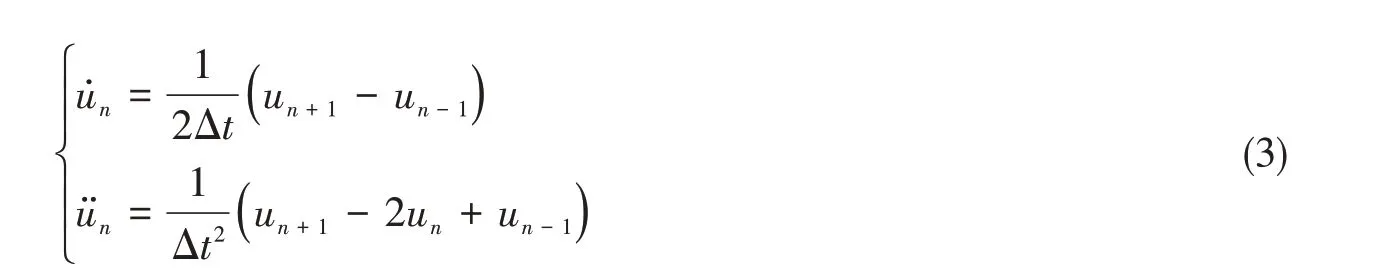
将式(3)代入式(2),整理得
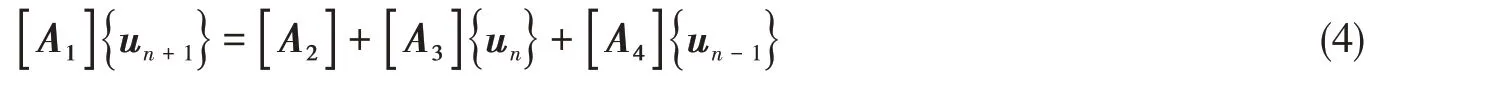
式中:
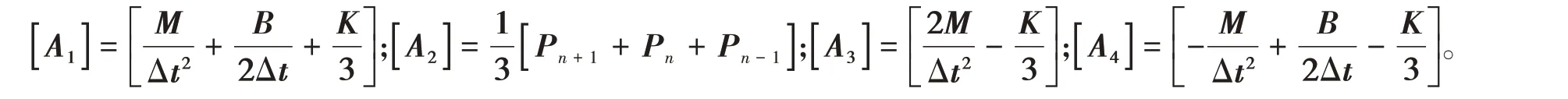
要求解式(4),只需给出初始u0和u1便可。u0为初始值,由系统给出,其中u1为

2.1.2 结构阻尼系数的影响
对于常规单体船来说,经过大量计算经验验证,通常取临界阻尼修正系数为0.05。但在对三体船的计算分析时,由于对此研究较少,有些文献中仍采用0.05 进行计算,但三体船特有的结构特点会使实际临界阻尼修正系数较单体船的更大,这种取法并不合理[10]。
因此,为合理地选取阻尼系数进行瞬态响应计算,本文首先采用直接积分法计算结构响应;分别取结构阻尼系数为0.05、0.10和0.12,计算各个方向上测点的应力响应曲线;使用PCL语言对模型实现砰击载荷以三角脉冲函数的形式施加,并充分考虑不同截面不是同一时间达到峰值的这一特点,以直接积分法计算出瞬态应力响应;最后分别选取外板、纵桁和横梁上的一个高应力单元进行不同结构阻尼系数下的应力响应对比,从而验证结构阻尼系数的不同对直接法瞬态响应分析结果的影响,结果如图2所示。
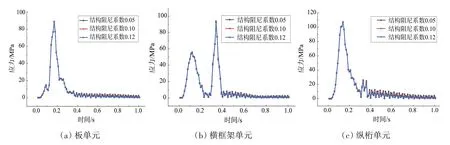
图2 不同阻尼系数下的直接法瞬态分析Fig.2 Direct transient analysis with different damping coefficients
其中对比的应力为各位置的Mises 应力,是利用各位置应力分量进行换算得到的。可以看出,对于板架结构的横梁单元、板单元和纵桁单元在结构的瞬态响应分析,同一测点在不同结构阻尼下的应力曲线几乎重合,说明在一定范围内可以任取结构阻尼系数对连接桥结构进行直接积分计算瞬态响应分析。本文采用0.10的结构阻尼系数进行后续计算的分析。
2.2 模态法瞬态响应分析
2.2.1 模态叠加法理论
模态法使用模态位移来解耦方程组,进而分别求解各个独立的微分方程得到结果,是一种对于大型结构求解效率高的方法。
将位移用模态坐标表示为

式中,[φ]为固有振型矩阵,则式(6)可写成
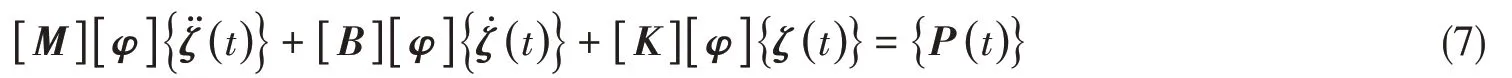
两边同时左乘[φ]T,得
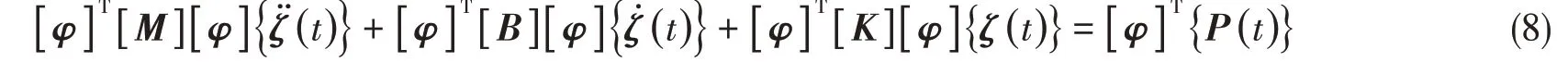
式中,[φ]T[M][φ]为广义质量矩阵, [φ]T[B][φ] 表示模态阻尼矩阵,[φ]T[K][φ] 是广义刚度矩阵,[φ]T{P(t)} 为广义力向量。
由于广义质量矩阵、模态阻尼矩阵和广义刚度矩阵均为对角矩阵,运动方程可表示为

式(9)可由中心差分法和Runge-Kutta 法求解,将结果代入式(6)中可求出位移。与直接法相比,模态法经过取舍后并不需要计算所有模态,特别是对于计算响应持续时间较长的工况,往往能够有效地提高计算效率。
2.2.2 临界阻尼系数的影响
在对模态法计算分析中,砰击载荷的计算方式与直接积分法中的一致。临界阻尼系数仍然取0.05、0.10 和0.12,选取模态数目为80 阶进行计算求解,得到高应力测点的Mises 应力响应曲线,所选取的3个高应力测点与直接积分法相同,结果如图3所示。
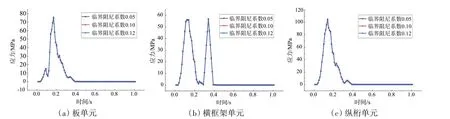
图3 不同阻尼系数下的模态瞬态分析Fig.3 Modal transient analysis with different damping coefficients
可以看出,与直接法相似,在一定范围内不同阻尼系数对结果影响较小,选取0.10 的临界阻尼系数能较为精确地预报初砰击载荷作用下的板架结构的响应。
2.2.3 模态数目对比
在模态叠加法中,模态数目的多少对分析的计算时间和精度都有着较大的影响。从模态叠加法理论可知,各阶模态(设模态数为n)所有有效质量的总和即为结构的总质量,如采用前p阶模态(p远小于n)来对结构的响应进行计算分析,只有当前p阶模态的有效质量的总和大于结构总质量的规定百分比时,取模态数目为p在分析中才被认为是足够的。通常动力学分析中规定,对于前p阶模态,要求在每一个主方向的响应计算中都至少包含90%的结构参与质量;当不满足参与质量要求时,则需要考虑增加所需计算的模态数目。
因此,为选取合理的模态阶数进行瞬态分析进而合理地计算砰击响应,本文使用MSC.Nastran 对板架结构前500阶模态进行模态分析,使用局部坐标系中四周固定约束的边界条件,计算不同阶数模态各方向有效模态质量的参与度,结果如表1所示。
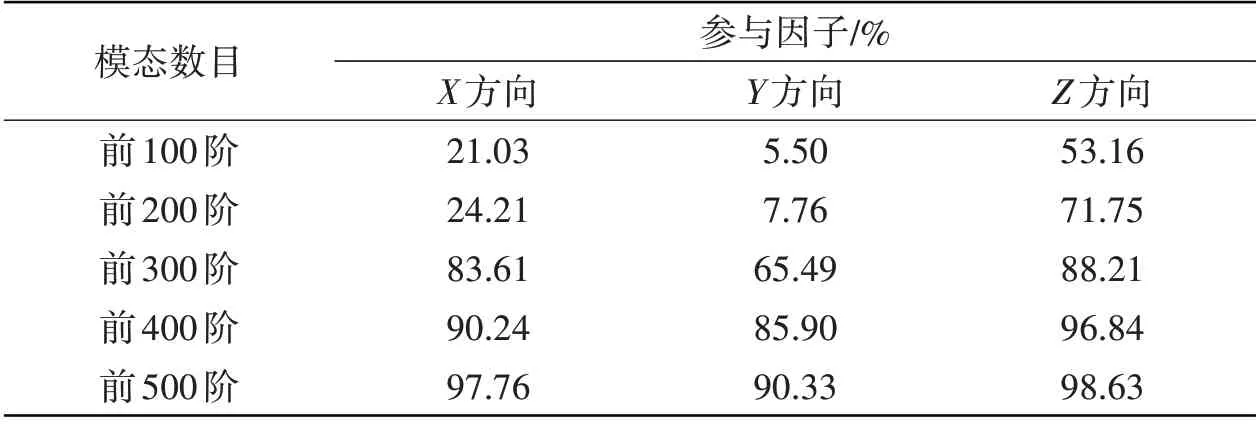
表1 质量参与因子Tab.1 Quality participation factors
为进一步验证模态数目对响应结果的影响,选取80、200、400 和500 阶模态进行模态法瞬态响应分析,相同的高应力测点选取对比如图4所示。可以看出,取前80阶模态与前500阶模态数目的计算结果偏差较大,基于前80阶模态得到的应力响应明显小于基于前500阶模态的计算结果,这是因为前者没能将高阶模态对结果的贡献考虑进来。但200 阶后应力曲线基本重合,且与直接计算法的瞬态响应结果也基本相同。
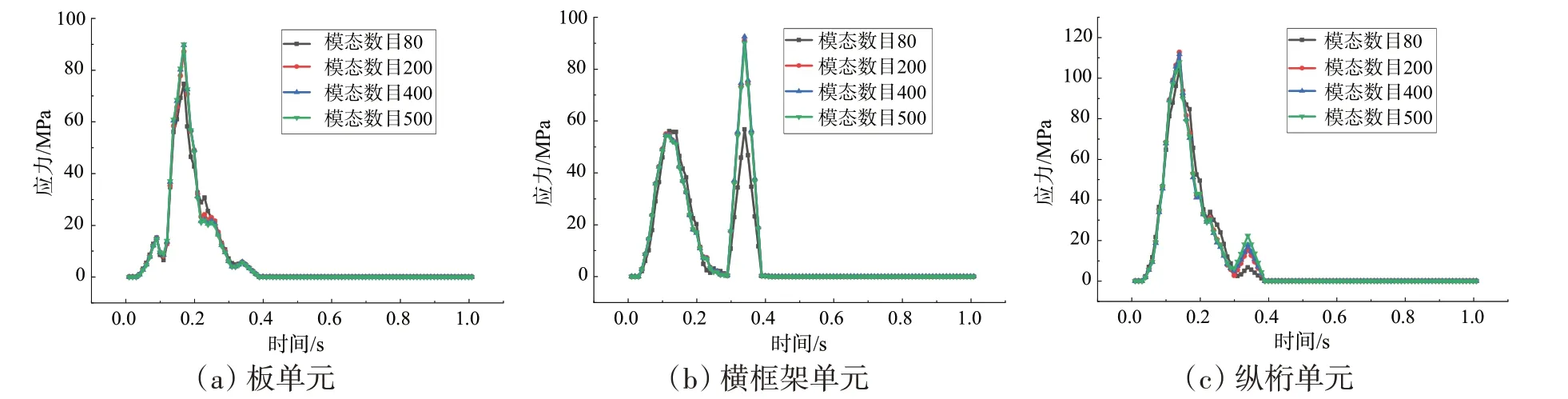
图4 不同模态数目下的模态瞬态分析Fig.4 Modal transient analysis under different modal numbers
由于在计算响应时间较短的情况下,直接法引入的人工阻尼对结果精度影响较小,与模态法相比两者结果较为相似,且直接积分法不易因忽略高阶模态的作用而产生误差。因此,对于作用时间较短的砰击载荷作用下的响应计算,采用直接积分法瞬态响应分析是更加合适的。
3 等效静力系数
为了对入水砰击过程中三维板架动态和静态响应建立联系,王辉[11]和于鹏垚[12-13]先后对等效静力系数进行了研究,对等效静力系数进行了定义:在某一工况下,对板架入水冲击进行动态响应分析,得到位置动态应力峰值;在同一工况下,加载板架上各位置压力峰值,得到静态应力,以及动态应力峰值与静态应力值的比值。此外,建立了砰击载荷作用下局部板架的等效静力分析方法,即将选取位置的静力峰值与等效静力系数相乘,其值便为选取位置的动态响应结果。本文对板架结构进行静力分析和直接法瞬态响应分析,进行相应位置的等效静力系数的计算。所选取的各类构件可能产生高应力的位置及其编号如图5所示。
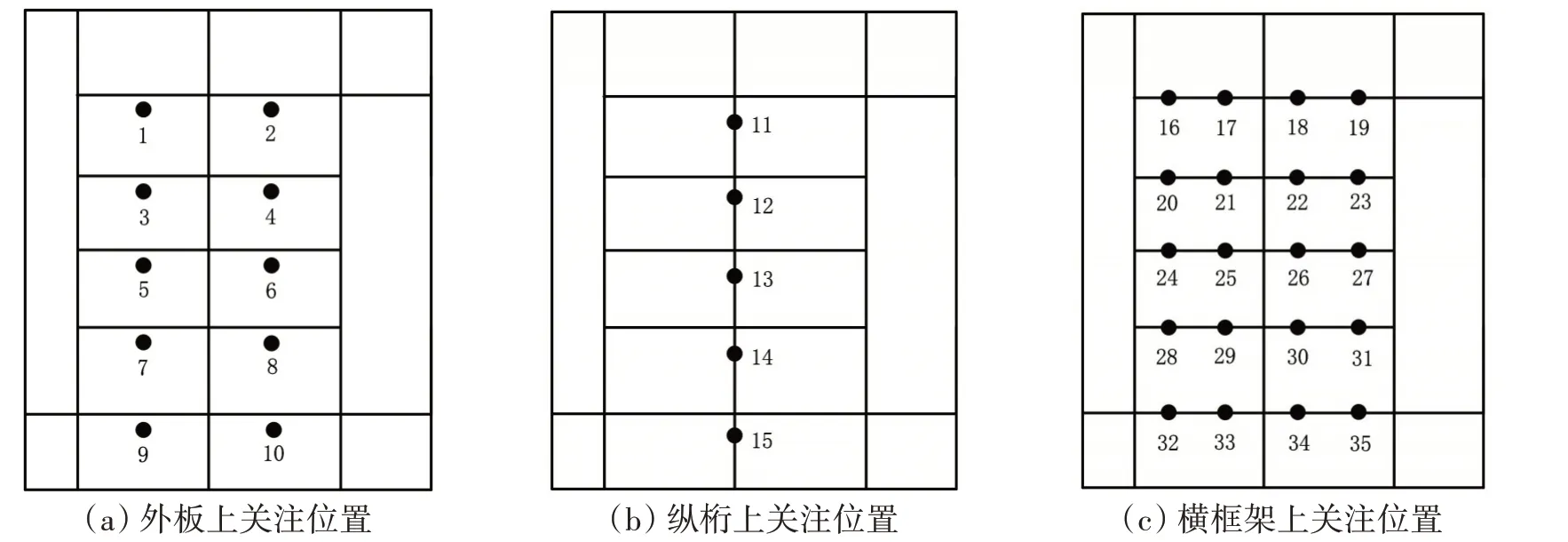
图5 高应力位置选取Fig.5 Selection of high stress location
文献[13]中虽对砰击速度、入水角度等影响因素进行了分析,但仅对简化模型进行了等效静力系数的分析对比,并未与实际船体结构模型的等效静力系数进行计算和对比验证。因此,本文就板架结构的边界条件和连接桥不同截面达到峰值所需时间不同对结果的影响进行了分析,并将简化模型和三体船连接桥片段模型中对应的高应力位置的等效静力系数进行对比,具体工况参数组合如表2所示。

表2 不同边界条件参数Tab.2 Different boundary condition parameters
为了对高应力位置进行等效应力系数计算,对外板、纵桁和横框架的高应力位置均进行了动态应力峰值计算,结果如图6所示。因横框架高应力位置选取较多,图中只展示了应力较大的位置。根据图6 结果,选取各类构件中应力响应较高的位置以及在不同边界条件作用下应力响应变化较大的位置进行等效静力计算,并将计算结果与三体船分段模型的等效静力系数结果进行分析对比,结果如图7所示。从图6 和图7 结果可以看出,当四周边界条件改变时,各位置的应力响应峰值和等效静力系数变化不大,但板架结构横框架截面的约束条件的不同在一些高应力位置的应力响应峰值和等效静力系数会产生较大的影响。因此,对于对称面载荷的施加应该尽可能与实际工况相符合。而通过与三体船连接桥模型的相应位置的等效静力系数对比可以发现,使用左右边界固结,前后边界为对称边界(对称面处施加简支边界条件)的情况下与实际连接桥模型得到的等效静力系数最为相似。而高应力位置9 和10 的等效静力系数有较大的误差。进一步分析发现,其位置靠近边界且被横框架的横梁所限制,导致静态计算结果有较大的误差,但因为横框架结构的存在导致其应力响应较小,对于后续强度计算影响较小,所以等效静力系数可以采用简化模型的数值。
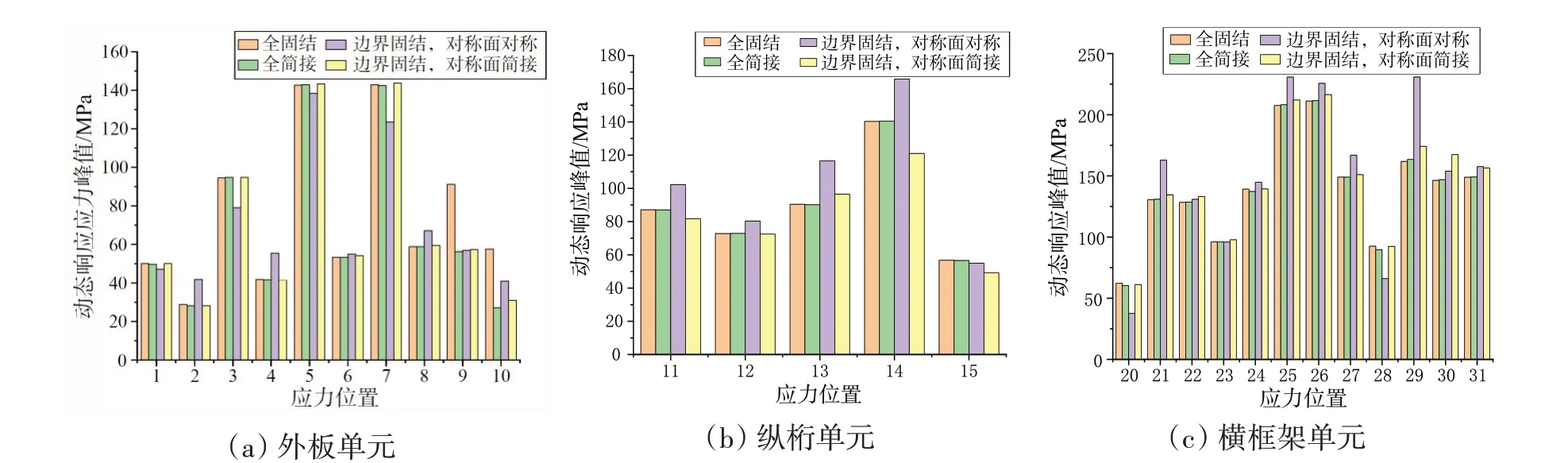
图6 不同边界对动态响应峰值的影响Fig.6 Influence of different boundaries on dynamic response peak value
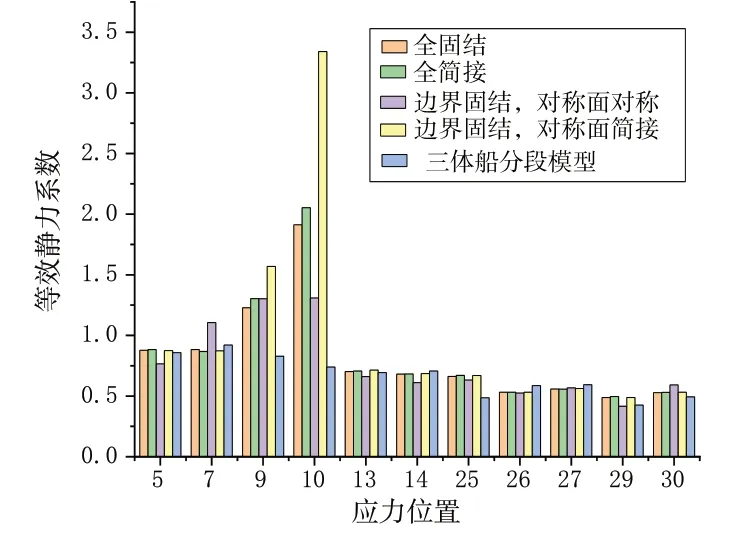
图7 不同边界对等效静力系数的影响Fig.7 Influence of different boundaries on equivalent static coefficient
此外,本文对不同截面到达压力峰值不同的时间效应所造成的影响进行分析,结果如图8 所示。可以发现,如果不考虑实际效应,其各位置的等效静力系数均为1 左右,这与实际情况是极为不相符的。因此,在对砰击载荷采用三角脉冲函数进行施加的过程中必须充分考虑其不同截面达到峰值时间不同的时间效应,而不能简单地作为同一时间达到峰值进行处理。
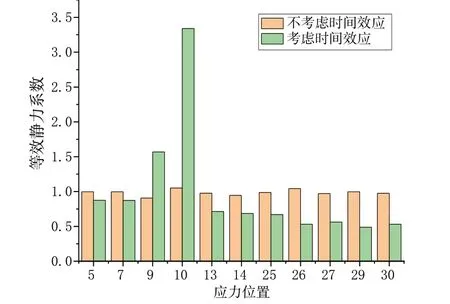
图8 是否考虑时间效应对等效静力系数的影响Fig.8 Influence of time effect on the equivalent static coefficient
4 结 论
本文通过对三维板架模型进行砰击载荷作用下的响应分析,比较选取了合适的方法进行瞬态响应分析,并验证了借助板架模型来得到等效静力系数这一方法的可行性以及影响因素作用,得到的具体结论如下:
(1)通过对砰击载荷作用下的板架结构进行瞬态响应分析后发现:无论基于哪一种方法,在一定范围内的阻尼系数变化对应力响应的影响都很小;此外,与模态叠加法相比,直接积分法能更好地反应板架结构在作用时间较短的砰击载荷作用下的瞬态响应,不容易因忽略高阶模态而产生误差。
(2)基于边界条件等因素对板架结构响应和等效静力系数影响的分析,发现四周边界条件对等效静力系数影响较小,但横框架对称面边界条件影响较大。因此,在进行等效静力系数计算时,四周边界条件取为刚性固定或自由支持均可,对于对称面的边界条件应合理地考虑实际情况选取。
后续还将基于本文得到的计算结果和相关结论进行连接桥局部结构的砰击强度分析,进而实现连接桥高应力位置屈服强度的评估预报。
