缓波型柔性立管涡激响应数值模拟

周 岳，桑 松，曹爱霞，朱 晓

（1.中国海洋大学工程学院，山东青岛 266100；2.青岛黄海学院智能制造学院，山东青岛 266427）

0 引 言

柔性立管涡激振动的三维数值模拟方法是当今海洋工程领域的热点问题，其中缓波型柔性立管是在柔性立管的一段布置浮力块组成的浮子段，浮立块提供的浮力使得立管构型成一定波形，用浮子段将连贯柔性立管的触地点和顶部悬挂点分隔开，从而减弱了波浪载荷及上部浮体运动对触地点的动态扰动。目前对于缓波型柔性立管的涡激振动研究较少,部分学者基于半经验模型的数值预报方法对细长柔性立管进行了数值分析。Birkoff 和Zarantanello[1]首次提出了非线性振子模型的概念。随后，Bishop 和Hassan[2]在此基础上提出了用Van der Pol振子方程来模拟尾流作用于圆柱上的流体力的方法。Facchinetti等[3]改进了尾流振子模型的动力特性，分别考虑了位移、速度和加速度对尾流振子的耦合影响。将不同耦合形式的预报结果与试验结果进行对比，发现通过加速度与涡激升力的耦合可以在一定程度上定量地反应刚性圆柱的涡激振动特性。郭海燕等[4]基于改进的尾流振子模型对输油立管的VIV 响应进行了预报。黄维平等[5-6]提出的尾流振子模型不仅考虑了流向耦合的影响，还考虑了非线性阻尼效应。近年来借助计算机技术的CFD 模型发展迅速，通过尾流振子模型与CFD 相结合的方法反复求解流体和固体耦合问题直到获得一个收敛的结果。赵婧[7]基于CFD 与CSD 方法对圆柱体的涡激振动响应进行了数值模拟，并进一步研究了带抑振装置圆柱体的涡激振动及抑振效果。秦伟等[8]建立了双自由度的涡强尾流振子模型分析悬链线立管的涡激振动。吴学敏[9]基于模型试验的结果对涡激力进行改进，实现了对深海立管大变形涡激振动进行分析。

将传统的CFD 方法应用于缓波型柔性管常会导致三个问题：第一个问题是由于缓波型柔性管长度较长和整体缺少约束，直接采用传统的CFD 方法对立管进行求解需要较长的计算时间和巨大的计算量来得到立管的运动；第二个问题是立管形状发生较大变化会改变特征向量，即结构问题不再是线性振动问题；最后一个问题是对于使用的网格运动技术难以编程，可能会导致网格扭曲而过早地停止计算。Holmes 和Constantinides[10]采用CFD 方法模拟带浮力块的深水立管，指出传统CFD 方法在处理存在弯曲或柔性较大的立管问题时存在网格难以划分问题。

为解决结构复杂的缓波型柔性立管涡激振动响应，本文基于Milan 尾流振子模型，通过OrcaFlex软件结合悬链线方程，考虑缓波型柔性立管的几何非线性及三维效应，同时针对浮子段浮力块的不同覆盖率研究了缓波型柔性立管的涡激振动耦合特性。

1 缓波型柔性立管涡激振动响应求解方法

缓波型柔性立管上的力主要是垂直于立管轴速度分量的函数，同时，立管截面上的力仅是局部流体速度下立管运动的力。因此我们可以关注局部流动的影响，假设提前知道了平均形状，并且立管后续的运动是小的，可以在一个拉直的流体网格上解决这个问题。同时，假定力由立管运动和局部流体速度的法向分量决定。

首先，我们根据立管结构、流速剖面和假设的阻力系数计算出一个估计的平均位置。同时计算了立管结构在其平均位置上的特征值和特征向量组成的模态响应。然后，我们将立管上每一段的流体流量分为法向分量和轴向分量，通过流体速度的法向分量计算流体力。经验表明，典型立管上的力是由速度的法向分量决定的，而轴向分量的影响在大多数流动条件下可以忽略不计。通过更改OrcaF⁃lex 中的LINE 单元，将缓波型布局的立管顶端到触地点的弧长长度及单位质量等效为垂直立管的长度与质量，提取原节点位置的轴向张力和节点弯矩等效到垂直立管的相应位置，使得等效前后的张力及弯曲特性一致，将问题转换为结构更简单的顶张式立管涡激响应进行快速求解。

2 缓波型柔性立管涡激响应数值模拟

2.1 缓波型柔性立管涡激响应数值模拟

按照缓波型柔性立管的参数建立模型，采用上述等效方法，及Orcaflex中的Milan尾流振子模型对缓波型柔性立管进行耦合特性数值模拟分析，某海域海洋立管参数如表1 所示，数值仿真结果如图1所示。

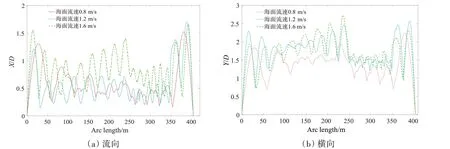
图1 不同流速下缓波型柔性立管的无量纲振幅Fig.1 Dimensionless amplitude at different flow rates

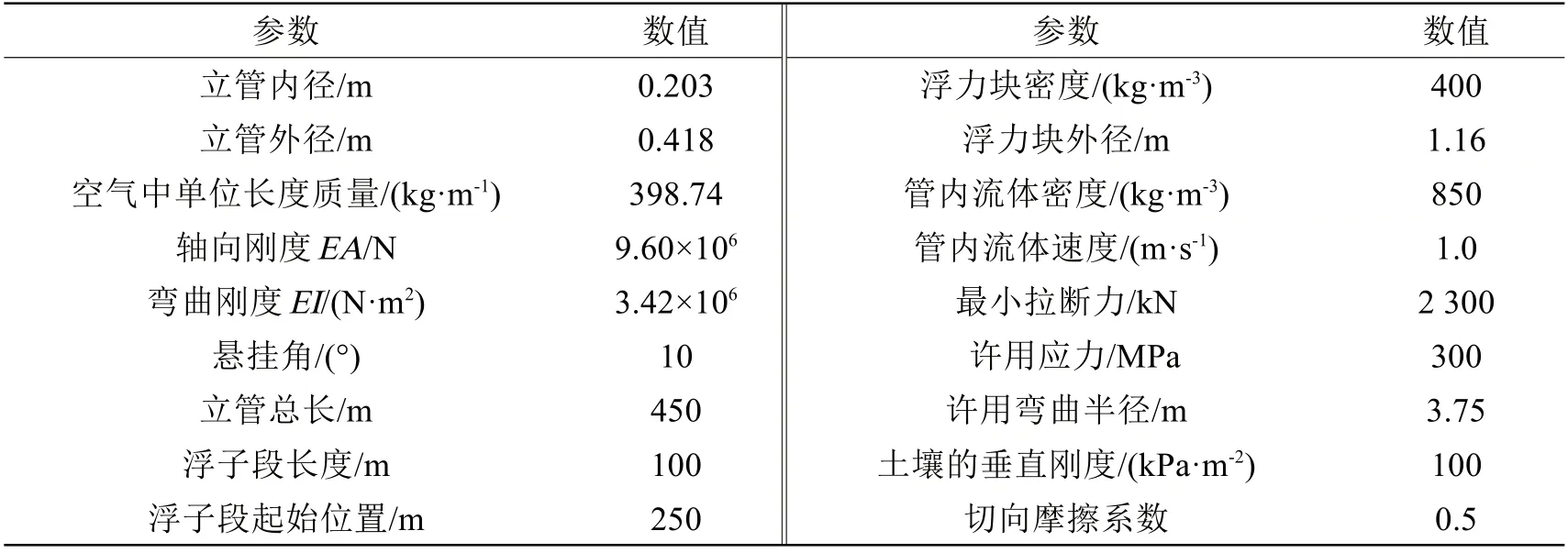
表1 缓波型柔性立管系统参数Tab.1 Parameters of lazy-wave flexible riser system

流体振子与管道运动方程为

设第n阶模态下管道横向振动的频率与振型分别为ωj和φj(z)，则方程（1）及（2）的解可分解为

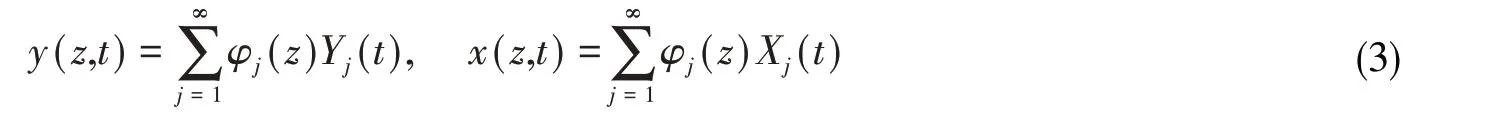
代入式（1）及（2）并因为振型正交，得到

式中，

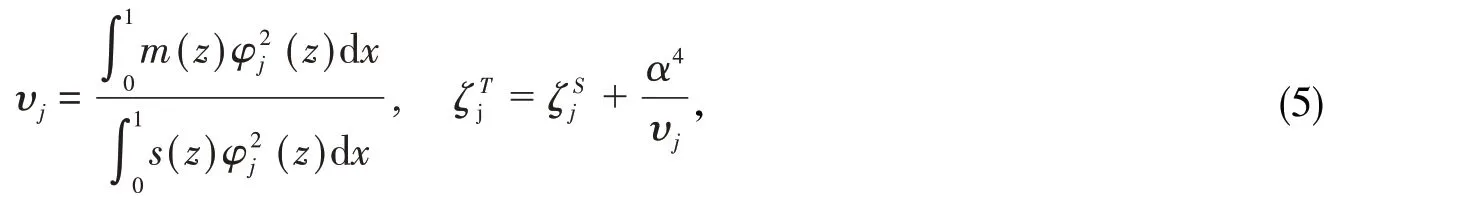
结构锁频共振幅值的表达式为

式中，Ij为振型形状函数，Fj为放大因子。

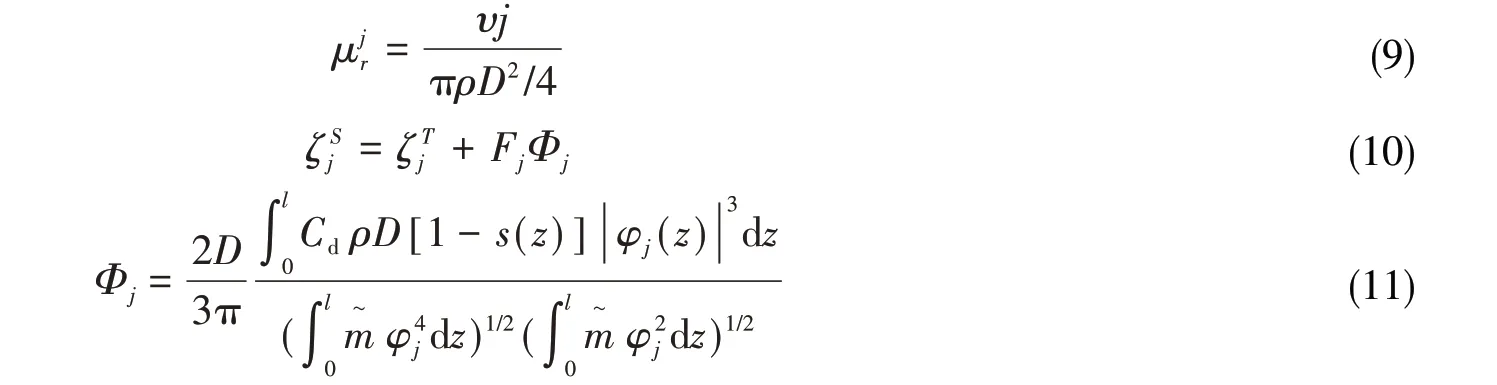
由方程（3）可知，得到Fj即可得到Yj，而Fj与是耦合的，可对式（8）及式（11）迭代求解得到锁振幅值。

从图1 可以看出，随着流速增大，立管涡激响应逐渐增大，流向和横向的无量纲位移都增大并且激发的模态更多，但是涡激响应在浮子段（250 m 到350 m）明显减小，说明浮力块减小了立管的涡激响应。因此对缓波型柔性立管的涡激振动响应研究，应关注浮子段的浮力块布置，探寻浮力块不同布置方案对缓波型柔性立管涡激振动的影响，为抑制缓波型柔性立管的涡激响应提供新思路。

2.2 浮力块布局对柔性立管涡激效应的影响

为了研究浮力块的布置对缓波型柔性立管涡激特性的影响，现研究浮子段在浮力块覆盖率不同的情况下柔性立管的涡激响应特性，浮力块不同覆盖率布置图分别通过OrcaFlex 建立模型如图2 所示，表2为不同浮力块覆盖率下柔性立管模态频率。

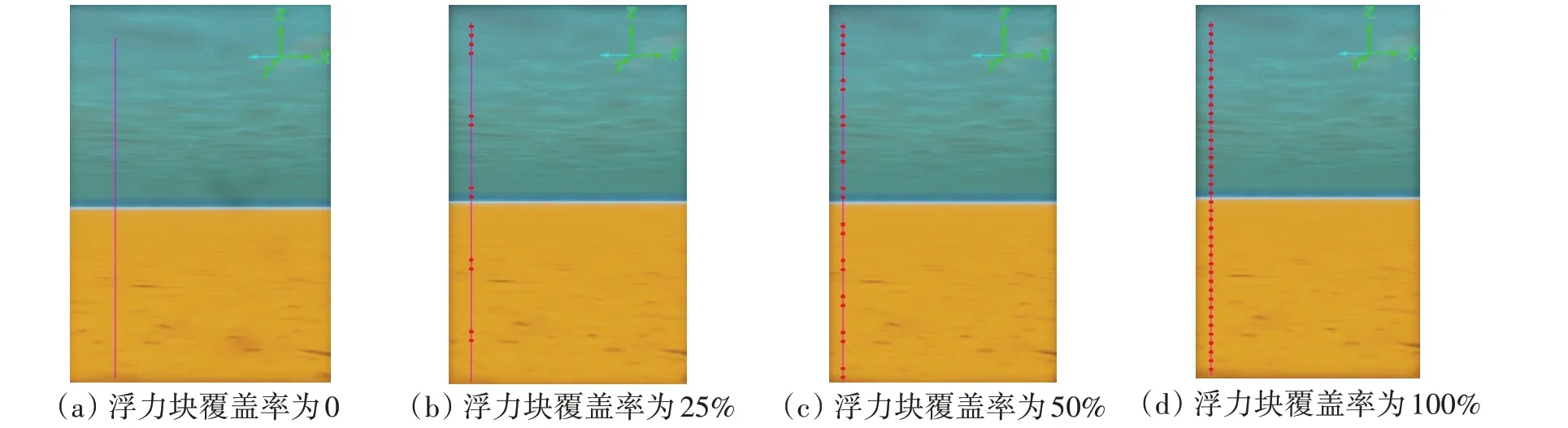
图2 浮力块不同覆盖率布置模型图Fig.2 Buoyancy block model with different rates of coverage

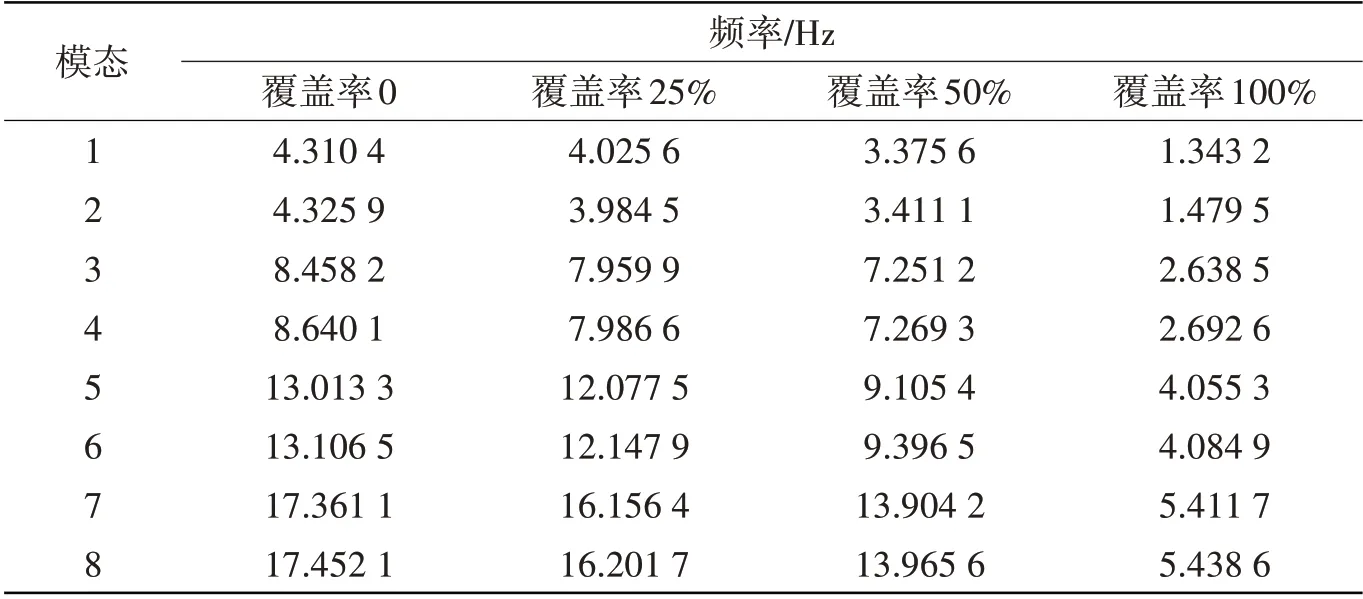
表2 不同浮力块覆盖率下柔性立管模态频率Tab.2 Flexible riser modal frequency under different rates of buoyancy block coverage

对于不同浮力块覆盖率的柔性立管进行振动响应分析，选取Z/L分别为0.25、0.5和0.75这三个点的数据，计算这三个点的顺流向和横流向的振幅时程曲线，并经过快速傅里叶变换，得到振动响应频谱图。通过这三个点的相关数据直观地观察立管沿轴线方向的振动响应相关特性，研究来流速度为0.2～1.0 m/s 时不同覆盖率柔性立管的涡激振动特性。限于篇幅，此处只给出浮力块覆盖率为25%的柔性立管在均匀流1.0 m/s 速度条件下立管各点涡激振动的横向和顺流向无量纲振幅时程曲线，如图3所示，表3为不同浮力块覆盖率下柔性立管的最大响应振幅及稳定时间的计算结果。

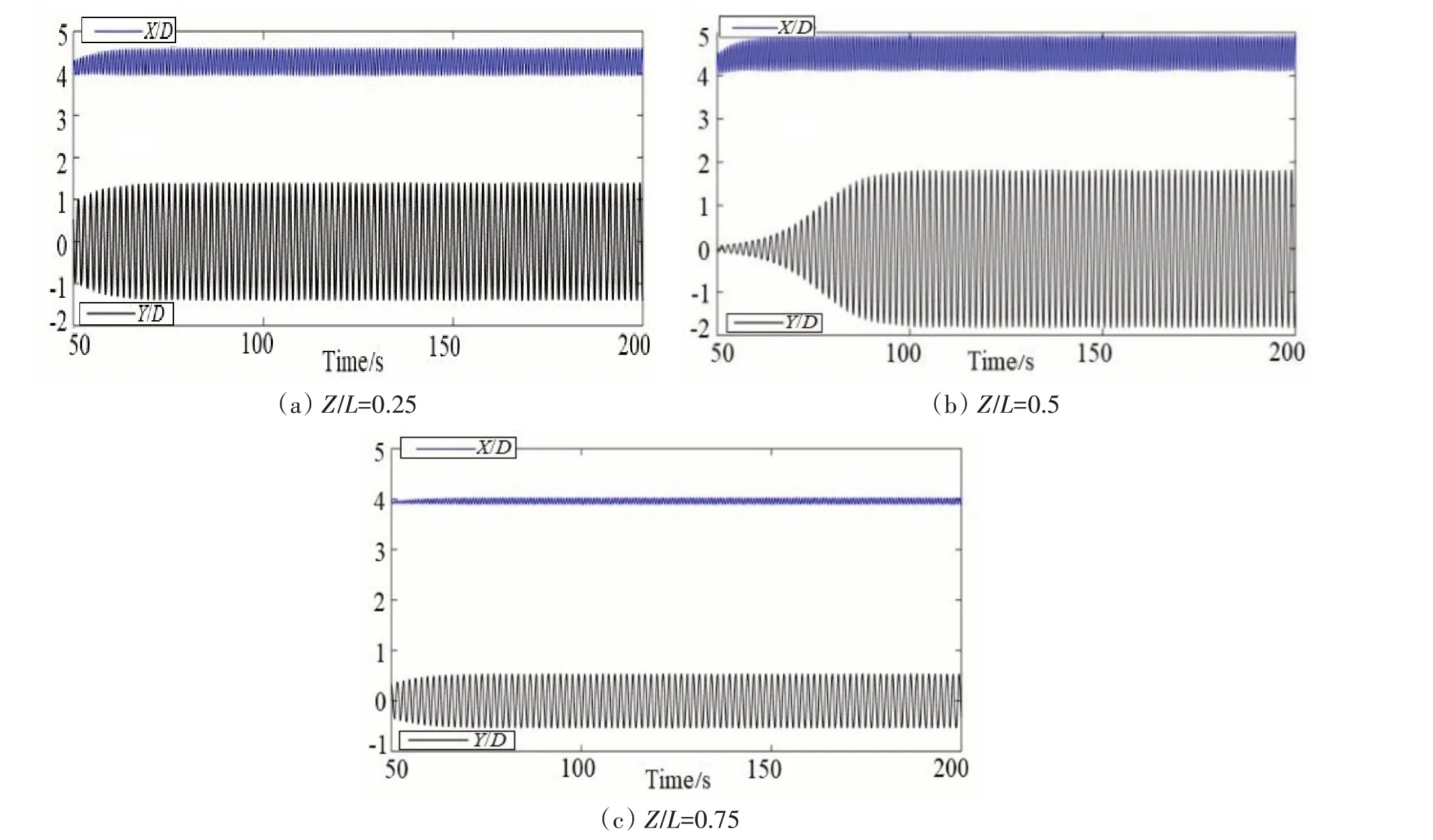
图3 浮力块覆盖率25%的柔性立管在均匀流1.0 m/s速度条件下的节点响应Fig.3 Node response of a flexible riser with a coverage of 25%at a uniform flow rate of 1.0 m/s

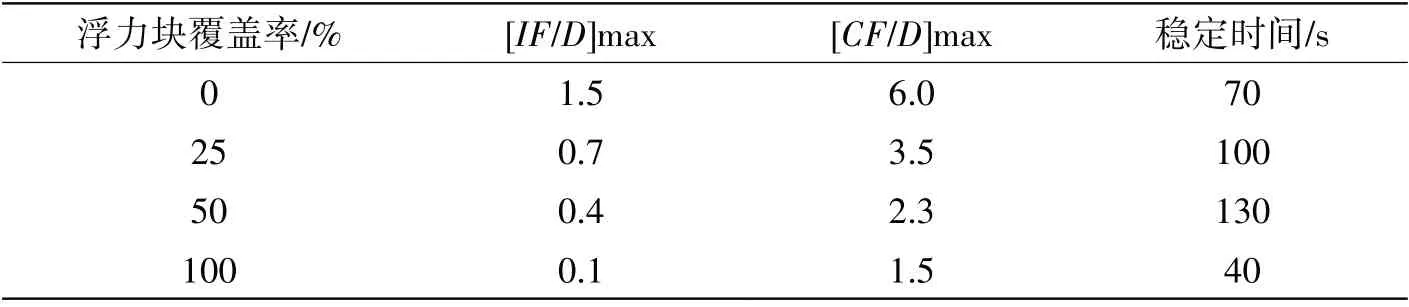
表3 不同浮力块覆盖率下立管的最大响应振幅及稳定时间Tab.3 Maximum response amplitude and stabilization time of riser with different rates of coverage

通过对表3 的数据分析可以得知，浮力块的覆盖率从0 增加到50%的过程中，柔性立管的来流向振动无量纲振幅最大值从1.5 减小到0.4，减小幅度超过70%，横向振动无量纲振幅最大值从6.0 减小到2.3，减小幅度超过60%，进入稳定状态的时间从70 s 增大到130 s，增加幅度约85%。不难看出，由浮力块覆盖率从0增加到50%的过程中，柔性立管来流向和横向振动的无量纲振幅最大值持续减小，但是减小幅度及幅值变小，进入稳定状态的时间增加幅度也减小，表明在浮力块覆盖率从0 增大到50%的过程中，整个柔性立管系统的响应变得更稳定。但是当浮力块的覆盖率增加到100%时，柔性立管的来流向振动无量纲振幅最大值从0.4减小到0.1，减小幅度约为75%，横向振动无量纲振幅最大值从2.3 减小到1.5，减小幅度约35%，进入稳定状态的时间从130 s 减小到40 s，减小幅度约为70%。发现浮力块覆盖率从50%增加到100%时，柔性立管来流向和横向无量纲振幅大幅减小，进入稳定状态的时间反而显著缩短，说明在浮力块覆盖率从50%增加到100%过程中，浮力块的增加可以显著减小立管涡激振动响应，尤其是来流向的振动响应，同时使柔性立管更快地进入稳定状态。对流速1 m/s情况下不同浮力块覆盖率的柔性立管流向和横向的振幅时程曲线做快速傅里叶变换，得到振动响应频谱图，如图4～7所示。

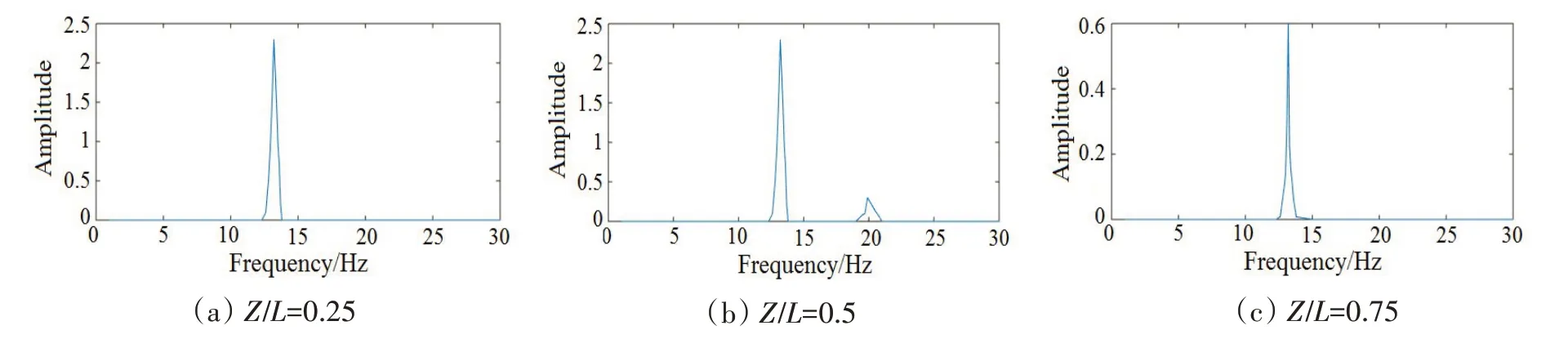
图4 浮力块覆盖率为0时柔性立管的振动响应频谱Fig.4 Vibration response spectrum of flexible riser(0 buoyancy block coverage)

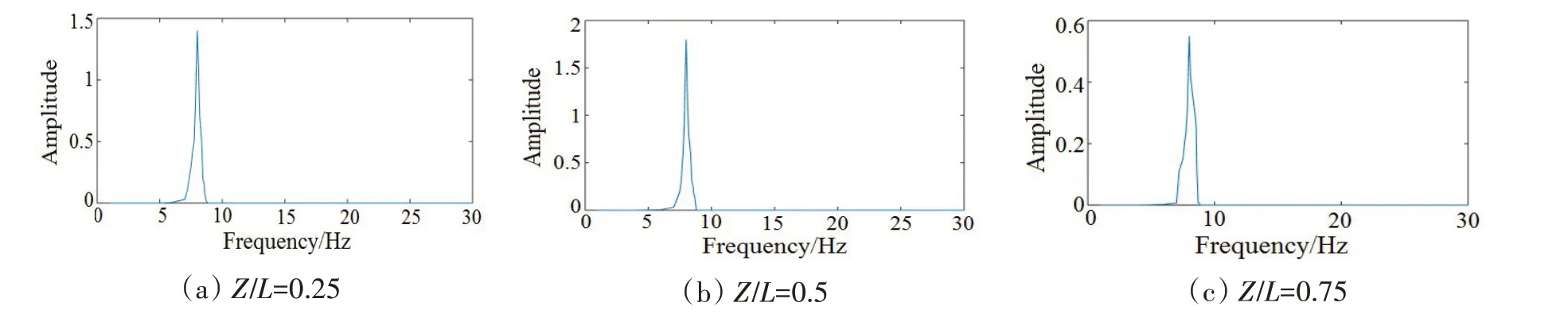
图5 浮力块覆盖率为25%时柔性立管的振动响应频谱Fig.5 Vibration response spectrum of flexible riser(25%buoyancy block coverage)

图6 浮力块覆盖率为50%时柔性立管的振动响应频谱Fig.6 Vibration response spectrum of flexible riser(50%buoyancy block coverage)

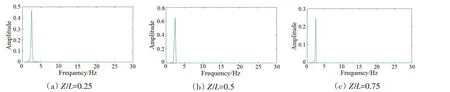
图7 浮力块覆盖率为100%时柔性立管的振动响应频谱Fig.7 Vibration response spectrum of flexible riser(100%buoyancy block coverage)

从不同浮力块覆盖率的柔性管道在1 m/s 来流条件下的振动时程曲线经过傅里叶快速变换的频谱图中，可以看出0覆盖率的管道各个位置的主振动频率在13.2 Hz左右，但是不同位置的管道振动频率的分布并不是完全一致的。在管道Z/L=0.5 处管道的振动频率谱出现了宽频谱，主频率在13.2 Hz左右，还有1个小峰值19.9 Hz，说明在管道中部出现了多模态叠加振动的现象。并且0覆盖率激发了6阶模态，随着浮力块覆盖率的增加，25%覆盖率的主频率约为8.1 Hz，激发了4阶模态，50%覆盖率的主频率约为7.3 Hz，激发了4 阶模态，100%覆盖率的主频率约为2.5 Hz，激发2 阶模态，表明浮力块覆盖率的增加可以减少涡激响应激发的模态，与增加浮力块覆盖率可以减小涡激振动响应特性一致。

2.3 柔性立管位移轨迹分析

图8～10为不同浮力块覆盖率下1.0 m/s流速下柔性立管不同位置轨迹图。

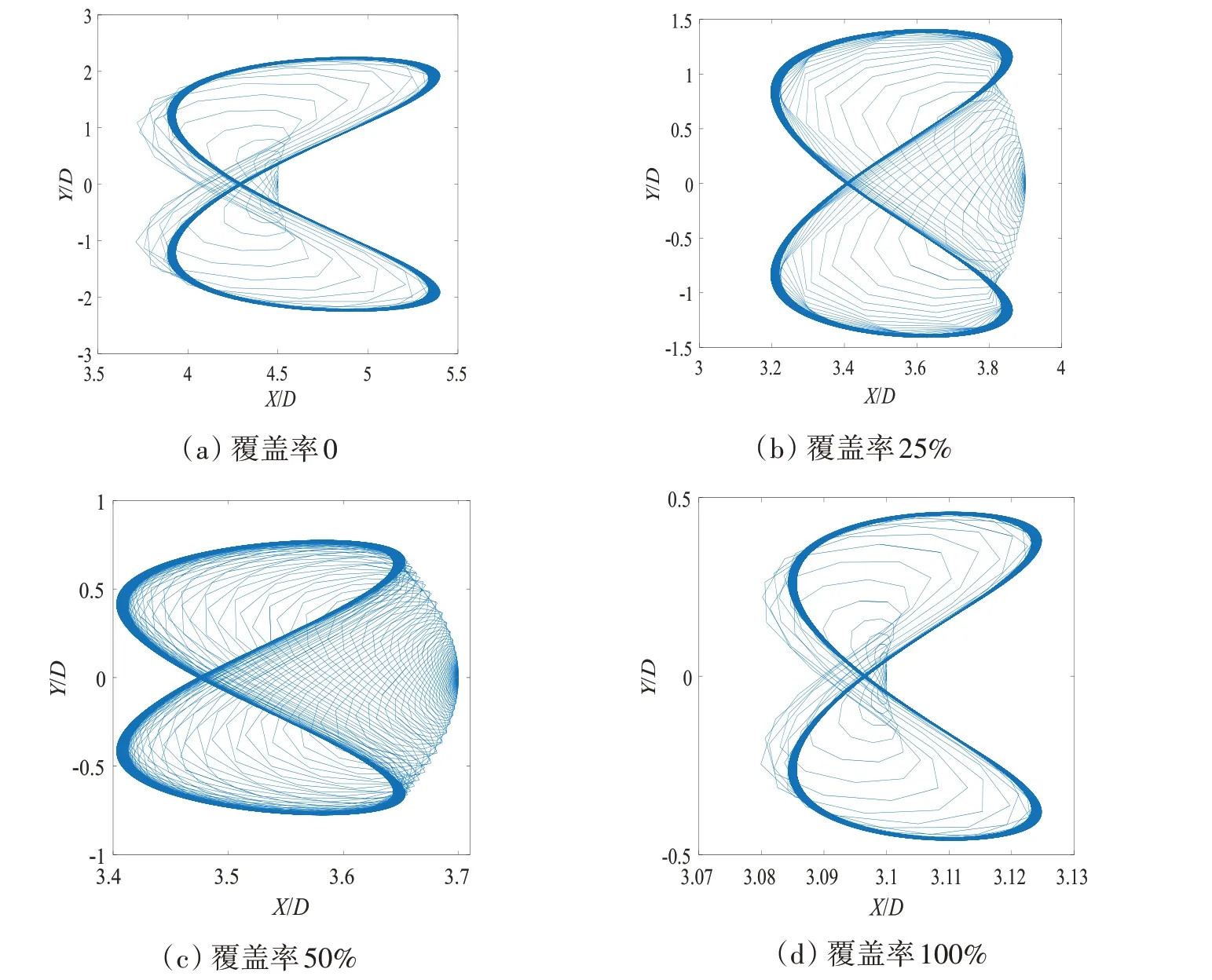
图8 Z/L=1/4处不同覆盖率下柔性立管轨迹图Fig.8 Track of flexible riser at Z/L=1/4 under different rates of coverage

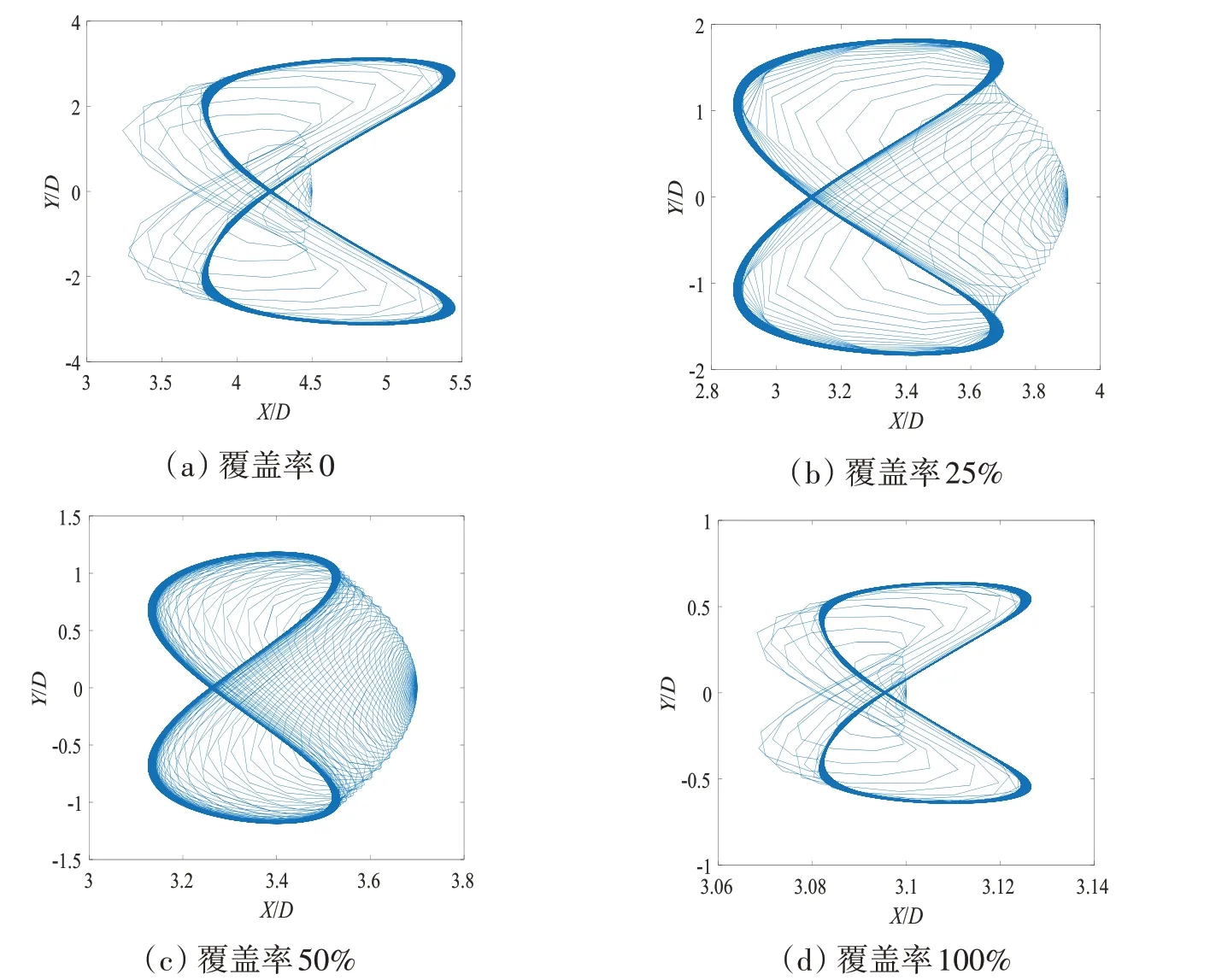
图9 Z/L=1/2处不同覆盖率下柔性立管轨迹图Fig.9 Track of flexible riser at Z/L=1/2 under different rates of coverage

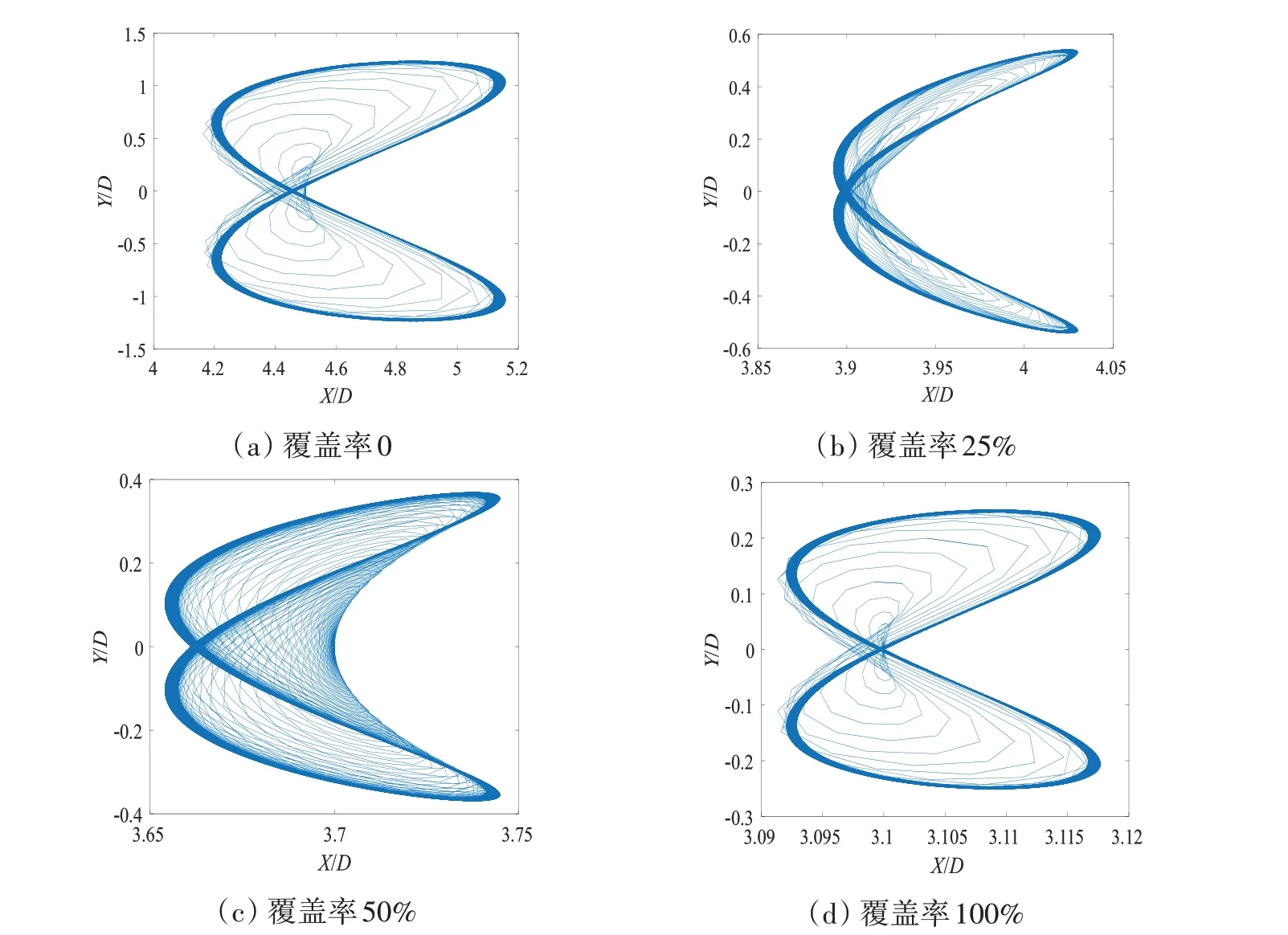
图10 Z/L=3/4处不同覆盖率下柔性立管轨迹图Fig.10 Track of flexible riser at Z/L=3/4 under different rates of coverage

从图中可以看出，当覆盖率从0增大到50%的过程中，柔性立管不同位置的运动轨迹逐渐变得复杂，且进入稳定的时间较长，说明柔性立管自身的涡激复杂性随着浮力块覆盖率增加变得更加显著。但是当浮力块覆盖率达到100%时又较快地进入稳定状态。浮力块随覆盖率变化，柔性立管质心偏移轨迹的总体趋势是随覆盖率增大逐渐减小，在浮力块覆盖率到达100%时，响应减弱到最小，再次说明浮力块覆盖率的增加减小了柔性立管的涡激响应。

3 结 论

由于缓波型柔性立管构型复杂且特殊，传统方法难以快速计算，本文基于Milan 尾流振子模型采用一种新的等效求解方法，通过OrcaFlex 软件及悬链线方程将复杂结构等效简化，考虑缓波型柔性立管的几何非线性及三维效应，同时针对浮子段浮力块的覆盖率不同研究了缓波型柔性立管的涡激振动耦合特性，得到以下结论：

（1）整体分析缓波型柔性立管的涡激响应中由浮力块组成的浮子段涡激响应明显小于相邻的裸管段。

（2）通过改变柔性立管浮力块的覆盖率发现，在整个柔性立管浮力块覆盖率增加过程中，浮力块的增加可以减小柔性立管的涡激响应，尤其是减小来流向的振动响应。在一定的浮力块增加范围内，柔性立管进入稳定状态的时间会增长，但是当达到100%覆盖率时，柔性立管进入稳定状态的时间显著缩短甚至小于裸管状态，这说明100%浮力块覆盖率下整个柔性立管结构在高流速情况下更加稳定。

（3）浮力块覆盖率的增加可以减少涡激响应激发的模态，与增加浮力块覆盖率可以减小涡激振动响应特性一致。柔性立管自身的涡激复杂性随着浮力块覆盖率增加变得更加显著，但是当浮力块覆盖率到达100%时又较快进入稳定状态。随着浮力块覆盖率变化，柔性立管质心偏移轨迹的总体趋势是随覆盖率增大逐渐减小，在浮力块覆盖率到达100%时，响应减弱到最小，再次说明浮力块覆盖率的增加减小了柔性立管的涡激响应。