艇桨耦合状态螺旋桨水动力与噪声数值预报方法研究

张 楠，李 亚，黄苗苗，陈 默

（中国船舶科学研究中心a.水动力学重点实验室；b.船舶振动噪声重点实验室，江苏无锡 214082）

0 引 言

在水动力学领域，潜艇模型快速性的数值模拟工作一般包括潜艇模型阻力数值模拟、推进器敞水水动力数值模拟以及带推进器潜艇自航水动力数值模拟这三项主要内容，流场数值模拟可伴随这三项内容开展，其中自航工况数值模拟的技术难点在于准确预报艇-桨相互作用，艇-桨相互作用也可以简称为艇-桨干扰或艇-桨耦合。在完成上述阻力、敞水、自航三项数值模拟内容之后，可按照基于模型试验的快速性预报方法，分析自航因子，外推预报实艇功率和航速。

长期以来，潜艇艇-桨干扰数值模拟一直是国际水动力学领域的重要内容。国际上对于艇-桨干扰流动与水动力的数值模拟进行了持续不断的研究，经历了长久的发展与验证，模拟方法从早期的用分布体积力代替螺旋桨的方法已经发展到目前常用的用滑移网格模拟艇后真实的螺旋桨运转的方法。近年来，国际上特别是美国，在此领域又取得了许多有价值的研究成果。

Alin 等（2010）[1]采用大涡模拟方法（LES）对全附体舰船与潜艇流动及流激噪声进行了计算尝试，计算了SUBOFF 潜艇模型（DARPA AFF8）带七叶大侧斜桨（INSEAN E1619）的绕流，随后又结合Light⁃hill声学类比计算了流激噪声。他对于螺旋桨的处理没有采用常用的滑移网格方法，而是采用了一种动网格类型的变形重生方法（D&R）。

Chase 等（2012）[2]采用基于重叠网格的求解器CFDShip-Iowa（V4.5）对SUBOFF 潜艇拖曳状态、自航状态以及自航模（自由自航）超越机动状态的水动力和流场进行了数值模拟，作者将MIT 开发的螺旋桨势流求解程序PUF-14也嵌入在该软件中。在艇桨干扰模拟中，采用的计算模型是全附体潜艇带E1619 螺旋桨。在自航与自航模操纵模拟中，对于螺旋桨采用滑移网格与PUF-14 计算这两种方法，直线航行时，两种方法差别不大，但当操纵运动时，特别在尾部流动分离与低进速系数下，两种方法的差别比较明显。

Liefvendahl等（2012）[3]采用大涡模拟方法计算研究了全附体SUBOFF潜艇模型带E1619螺旋桨的水动力和负荷脉动问题，螺旋桨模拟采用动网格方法。作者的数值模拟捕捉到了大尺度非定常相干结构，计算了围壳与尾翼流动结构以及艇体边界层在尾部的相互干扰流动特征，分析了在尾部逆压梯度作用下螺旋桨入流的形成过程，将这些流动特征与螺旋桨推力、扭矩以及叶片上的负荷进行了相关，并与单独艇体和单独螺旋桨的计算结果进行了对比分析。

Kim 等（2014）[4]发展了一种耦合刚体运动（RBM）与非定常RANS（URANS）的数值模拟方法，对于SUBOFF潜艇带E1619桨的拘束模状态与自航模状态绕流进行了数值模拟。在拘束模偏航计算中，利用移动参考系和滑移网格两种方法来考虑螺旋桨运转的影响。在自航模回转计算中，利用驱动盘模型和滑移网格方法来考虑螺旋桨运转的影响，计算了三自由度的艇体运动，分析了艇、桨、舵三者的相互干扰。

Norrison 等（2016）[5]采用大涡模拟方法对实尺度全附体Joubert 潜艇的艇-桨干扰流动进行了数值模拟。雷诺数达到Re= 1.68 × 108与Re= 3.36 × 108。结果表明，绕实艇的流动拓扑结构与模型尺度相似，符合随雷诺数增高流动结构趋于紧致与收缩的经典认识。螺旋桨采用DSTG115-1 五叶桨与DSTG057-1七叶桨，与五叶桨相比，七叶桨的叶中负荷更高，梢涡破碎更早，尾流掺混更强。

Carrica 等（2016）[6]对于Joubert BB2 潜艇自航模操纵工况进行了试验和数值模拟研究，网格数达到3550 万。自航模试验在MARIN 水池开展，包括近水面与深潜直航、回转、垂直面与水平面Z 形机动、应急上浮等。他们将试验数据做成数据库，用以验证操纵性预报方法的准确性。作者采用两种求解器进行潜艇自航模操纵工况数值计算，一种是ReFRESCO（荷兰MARIN牵头，葡萄牙IST、巴西USPTPN、荷兰DUT、荷兰RuG、英国UoS、瑞典CUT、加拿大UNB 等大学和科研院所联合开发的软件），另一种是REX（CFDShip-Iowa V4.5+Magnus）。采用体积力法和滑移网格法模拟螺旋桨旋转，采用重叠嵌套网格模拟潜艇运动。对于深潜状态三个航速下的潜艇直航运动、近水面垂向控制运动、操尾舵定深回转运动、操围壳舵与尾舵的Z形机动、应急上浮等都进行了详细的数值模拟、验证和分析，研究工作全面而且深入。

Carrica 等（2018）[7]利用1700 万到1 亿3 千万网格对于Joubert BB2 近水面波浪状态下运动特性进行了进一步的数值模拟分析，波浪状态主要考虑的是顶浪规则波。对于静止与波浪状态四个围壳浸深的潜艇近水面自由自航特性进行了数值模拟，利用滑移网格模拟螺旋桨旋转，采用重叠嵌套网格模拟潜艇运动，潜艇尾舵为X 型舵，作者采用PID 控制器实现对于尾舵的操舵控制。Carrica 等（2016，2018）[6-7]的工作达到了很高的研究水平，可以称为目前船舶领域CFD技术的标杆。

随着国际上对艇-桨干扰流动数值模拟研究的蓬勃开展，自航状态船舶尾后螺旋桨辐射噪声的数值预报问题也逐渐进入研究者视野。近年来，也有一些研究问世，但相较艇-桨干扰流动问题的模拟研究而言，艇-桨干扰流激噪声的模拟研究还是比较少的，而且国外在计算螺旋桨噪声时常用的是Lighthill所创立的声学类比方法，近年来主要用的是FW-H声学类比方法。

Lighthill（1952）[8]创立了声学类比方法，起初主要处理的是喷射噪声问题。在声学类比方法里，流动特征（声源）通过求解合适的非定常流动方程得到，控制方程可以是可压缩的流动方程，也可以是不可压缩的流动方程，将求出的流动声源代入声学类比方程的远场解中，通过格林公式来预报远场噪声。声学类比方法的研究思路就是使用CFD 技术求解非定常流场，作为等效声源项输入到声场计算中，然后利用波动方程的解，将声源项产生的脉动进一步辐射到外场。从理论上讲，只要知道流体运动的物理特性，无论是运动源还是力源，从Lighthill 方程出发都能求解其声辐射，流体运动与声辐射看似独立的两个物理现象从此联系起来，流体动力声学作为一门学科从此发展起来。随后，运动体引起的流动噪声问题也逐渐进入学者的视野。1955年，Curle[9]采用Kirchhoff方法将Lighthill理论进行推广，导出了著名的Curle 方程，该方程可以处理静止固体边界的影响。从Curle 方程可知，一个四极子源与固体边界的相互作用会产生新的低阶的偶极子源，辐射效率增强，这正反映了声学的复杂性。随后在1969 年，Ffowcs Williams 和Hawkings[10]应用极为有效的数学工具——广义函数法将Curle 方程进行拓展，使之可以处理固体边界在流体中运动的发声问题，得到了经典的FW-H 方程。1974年，Gold⁃stein[11]用格林函数方法推导出了广义的Lighthill方程。从这个方程我们可以清晰地知道Curle 方程和FW-H 方程均是该方程的特定表达。上述基于Lighthill 思想的各种方法统称为声学类比方法。在近代逻辑学中，类比法是根据两个（或两类）不同对象的部分属性相似，而推出这两个（或两类）对象的其他属性也可能是相似的一种推理方法。类比法是归纳法和演绎法的中间状态，其推理方式是从特殊到特殊，即从一个对象的特殊知识过渡到另一对象的特殊知识。

在Lighthill方程提出之后，Powell（1964）[12]将涡量描述引入该方程，进一步研究了涡运动和声产生之间的联系，推导出了Powell方程（涡声方程），开创了涡声理论，这一理论实质上是Lighthill理论在低马赫数下的一个演化。Powell 方程指出：涡是低马赫数下等熵绝热流动发声的根源。由于涡量分布往往集中在狭小的流动区域，所以它是紧致的偶极子源。研究者普遍认为，Lighthill 理论在预报流动噪声方面有实用价值，而在探索流动发声的内部机制方面，Powell理论则以其简洁深邃的内涵显示出了极大的优势。Howe（1975）[13]进一步发展了涡声理论，引入驻焓(stagnation enthalpy)的概念，考虑了熵变化和平均流对流动发声的影响，导出了描述声音在气流中传播的非齐次方程——Howe 方程。Howe方程是描述由于涡量和熵的变化以及其相互作用而发声的声学普遍公式，它也描述了与声音相关联的非线性现象的相互作用。Howe方程指出，如不存在涡旋和熵梯度，则气流不会发声，声源只集中在那些存在有涡量及熵梯度的区域。Howe 方程只有在无旋和等熵时才是封闭的，多数情况下，此方程不封闭，只有再引进另外的旋度及熵的扰动量方程才能求解。Howe（2003）[14]进一步指出：气体的非定常粘流运动是声音、涡旋和熵运动成分的叠加和相互作用组成的，非线性效应导致上述运动的相互转变，这些问题是摆在连续介质力学和气动声学面前的艰巨任务，当然，这些内容也远远超出一般流动声学的研究范畴。

在FW-H 声学类比方程建立之后，许多学者致力于求出远场解。Farassat（1981）[15]、Farassat 与Brentner（1988）等[16]、Francescantonio（1997）[17]、Brentner 与Holland（1997）等[18]、Casalino（2003）[19]在声学远场解的推导研究方面做出了重要贡献。在声学计算结果处理技术方面，Wang、Lele 与Moin（1996）[20]提出了出口边界修正方法。Mendez 等（2009）[21]研究了开口与闭口积分面的影响，认为使用基于压力的公式结合出流盘面平均技术给出的结果最好。Nitzkorski 与Mahesh（2014）[22]提出了“dy⁃namic end cap”处理方法。

在国际水动力学领域，Bensow等（2016）[23]采用OpenFOAM开源软件中的大涡模拟与FW-H声学类比方法对在船舶尾后运转螺旋桨的空泡噪声进行了计算研究，并与试验进行了对比。利用VOF 结合显式质量传递模型计算空泡，模拟中忽略了水面的影响，螺旋桨运转采用滑移网格方法。计算模型包括单独船体、单独螺旋桨以及带桨船体，计算工况包括两个状态的空泡噪声，一个状态的无空泡噪声。对于某状态的空泡噪声，与试验结果相比，计算结果在400 Hz以下小了约20 dB，在400～1 100 Hz，计算结果与试验结果吻合尚可。

Ianniello等（2014）[24]采用不可压缩RANS方法结合FW-H声学类比方程对于某巡逻艇模型在定常直航下的螺旋桨噪声与船体噪声进行了预报。作者通过数值计算明确指出，尽管水中船用螺旋桨转速较低，但也不能忽视四极子噪声。厚度噪声、负荷噪声分量对远场压力的贡献非常有限，主要噪声源应是流场中的速度脉动，特别是在无空泡产生的情况下，桨叶梢涡的发放与向下游传播才是最主要的噪声源。作者将水动力与噪声结果进行了对比分析发现，由于船体的存在，出现了明显的散射。

Ianniello等（2016）[25]采用FW-H 声学类比方法计算了无空泡状态下的螺旋桨噪声，详细分析了面积分对噪声计算结果的影响。他经过理论分析和数值计算发现，与航空中旋翼的主要噪声是厚度噪声和负荷噪声不同，水中螺旋桨的主要噪声是螺旋桨的尾流/涡流所发放的噪声，非定常非均匀的流场是主要噪声源。

在国内，朱锡清（2008）[26]深入研究了螺旋桨噪声的机理、种类和预报方法，详细阐释了推进器噪声的成因和种类、非空泡螺旋桨离散谱（线谱）噪声预报与宽带噪声的理论分析、螺旋桨空泡噪声的预报以及推进器（螺旋桨）噪声的控制等方面的研究方法与成果。熊紫英等[27]采用面元法对于无空泡螺旋桨非定常推力脉动及其诱导线谱噪声进行了计算分析。

作者以往对于潜艇流场、水动力与流激噪声开展了一些数值模拟研究[28-38]。前期主要是利用RANS 方法对潜艇带推进器自航的流场与水动力进行了数值模拟，在流场与水动力模拟的基础上，近年来又利用LES结合FW-H声学类比、Kirchhoff方法与Powell涡声方程等声学计算技术对潜艇流激噪声进行了数值预报计算探索，这些流声耦合研究工作是本文研究的基础。本文即采用LES结合Powell涡声方程对SUBOFF潜艇带AU5-65螺旋桨在敞水与自航工况下的流场和流激噪声进行了数值模拟，研究了LES 结合Powell 涡声方程对螺旋桨水动力与噪声的预报能力。本文中的LES 方法利用商用软件Fluent完成，Powell涡声方程数值预报方法通过自编程序实现。目前国内外采用Powell涡声方程计算流激噪声的公开文献还不多见，作者前期对于Powell涡声方程预报方法的探索请见文献[35]。

1 数值计算方法

1.1 大涡模拟方法

将N-S方程进行网格滤波，从而得到大涡模拟的控制方程。滤波之后，则大于网格体积的流动结构通过直接求解N-S方程得到，而那些小于网格体积的流动结构则通过亚格子涡模型来进行模拟。滤波变量由下式定义：

式中，φ(x)为流动变量，D为流体域，G为滤波函数。取滤波函数为

式中，V为计算网格的体积。

滤波后的连续性方程和N-S方程可以表示为

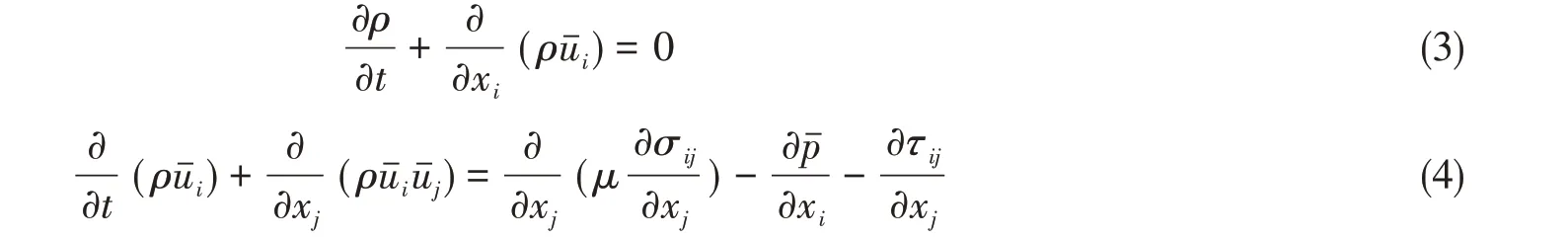
式中：σij为分子粘性引起的应力张量；τij为亚格子应力，需用亚格子模型进行模拟。

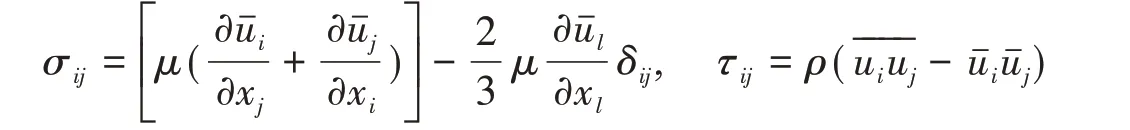
本文采用动态Smagorinsky模型对亚格子应力进行模拟，这种模型是Germano在1991年提出的[39]，通过对最小可解尺度的信息进行采样，然后利用这些信息来模拟亚格子尺度应力，此模型在接近壁面边界时给出了正确的渐近特性，而且并不需要阻尼函数或者间歇函数。此模型还能够考虑逆散射的影响。Lilly（1992）[40]利用最小二乘法对此模型进行了改进，这个办法提供了一个自洽的动态模型，可以在每个空间网格点、每一时间步上计算模型参数C。

引入布西内斯克（Boussinesq）假设，

1.2 Powell涡声理论

作者对于Powell 涡声方程的研究请参见文献[27]，本文作简要描述。在研究湍流诱发噪声问题时，关键的一步就是构建流动声源数学公式，也就是如何在数学表达上将流体运动转换为声源。Lighthill建立的声学类比方法是将雷诺应力、压力、剪应力进行组合作为声源，通过面积分和体积分得到远场辐射噪声，在工程实际中发挥了巨大作用，但声学类比理论尚不足以深入了解流动发声的机理和细节。因为众所周知，涡会产生噪声，而在声学类比理论中没有辨识出涡动力学特征，且Lighthiil应力张量在空间分布比较疏散，不利于计算，但涡量的分布相对集中，属于紧致声源，便于计算。在低马赫数流动中，涡旋结构一般而言都是紧致的，即涡旋结构尺度相对声波波长而言是小量。Powell深入研究了流体动力与噪声之间的关系，并将它们与涡运动联系起来，得到了涡运动产生噪声的机理与控制方程。

本文求解的Powell涡声方程表达为

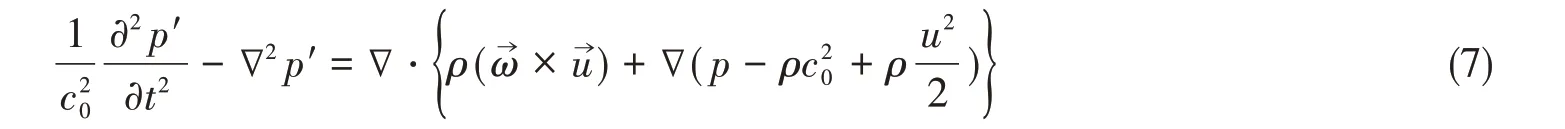
关于Powell涡声方程的远场解，利用三维波动方程自由空间格林函数

可将Powell方程的远场解表达为

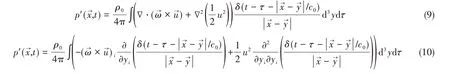
注意到格林函数的下列关系：

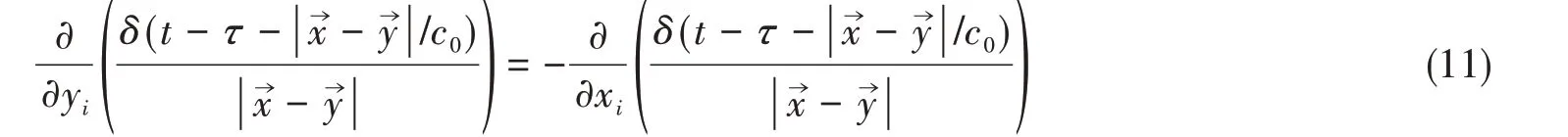
所以可将式（10）改写为

进一步利用δ函数的性质可得

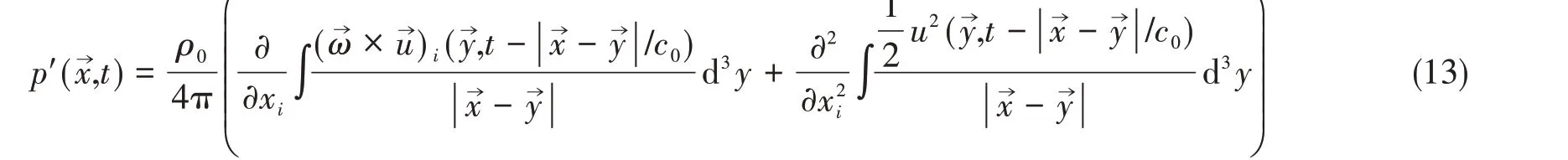
1.3 数值求解

时间项采用二阶隐式格式离散，动量方程采用限界中心差分格式离散，压力速度耦合采用SIMPLE算法。利用代数多重网格（AMG）方法加速收敛。计算中时间步长Δt=1×10-5s。壁面y+≈0.2～15。采用FFT结合Hanning窗处理非定常信号时间序列。

1.4 边界条件

敞水工况采用边界条件为

速度入口：螺旋桨前方5倍桨径处，设定来流速度的大小与方向。

压力出口：螺旋桨后方10倍桨径处，设定相对于参考压力点的流体静压值。

壁面：螺旋桨表面，设定无滑移粘附条件。

外场：距离螺旋桨5倍桨径，参数设置同速度入口。

计算中采用全域模型，不含对称面。见图1（a）。

自航工况采用边界条件为

速度入口：艇艏前方1倍艇长处，设定来流速度的大小与方向。

压力出口：艇艉后方2倍艇长处，设定相对于参考压力点的流体静压值。

壁面：潜艇与螺旋桨表面，设定无滑移粘附条件。

外场：距离艇身1倍艇长，参数设置同速度入口。

计算中采用全域模型，不含对称面。见图1（b）。

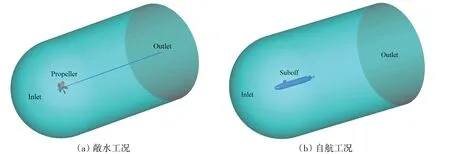
图1 计算域Fig.1 Computational domain

2 计算模型与网格

SUBOFF 潜艇模型主体长为4.356 m，其前体长为1.016 m，平行中体长为2.229 m，后体长为1.111 m；艇身最大直径为0.508 m；桨盘面位于距艇艏4.260 m处；指挥台围壳为一立柱体，其导边位于距艇艏0.924 m 处，随边位于距艇艏1.292 m 处，其水平截面为两椭圆相交而成；指挥台上部为一外凸的顶盖；四个尾翼形状、大小都相同，其横截面为NACA0020翼型，对称布置于艇身上下左右。

AU5-65 螺旋桨模型直径为0.24 m，叶数为5，螺距比为0.782，盘面比为0.65，毂径比为0.18，后倾角为10°。

计算模型与网格如图2 所示。敞水工况所用网格数为1 083 万（静止区域453 万，旋转区域630万），自航工况所用网格数为1 937万（静止区域1 307万，旋转区域630万），网格数量的确定参照了以往网格收敛性研究经验[28-38]，自航算例在本单位并行系统上利用10 个节点（200 核）计算，需要1 周时间达到稳定收敛。包裹螺旋桨的圆柱体内网格为四面体非结构化网格，圆柱体之外的网格都为六面体结构化网格。对于潜艇指挥台围壳、尾翼与螺旋桨周围的网格进行加密处理。

图2 潜艇与螺旋桨计算模型及网格Fig.2 Computational models and meshes of submarine and propeller

3 计算结果分析

3.1 水动力与流场计算结果分析

为了验证计算方法的有效性，先从计算水动力入手，进而计算涡旋流场，最后计算流激噪声，采用层层递进的验证途径。

对于敞水工况，采用与试验一致的等转速变航速的方法进行螺旋桨水动力数值模拟。利用滑移网格方法使螺旋桨以设定的转速n旋转，改变多个来流水速V，从而计算多个进速系数J0下的螺旋桨推力T0、转矩Q0。推力系数、扭矩系数及敞水效率的定义如下：

式中，D为螺旋桨直径，ρ为流体介质密度。

计算中的转速与敞水试验保持一致为25 r/s，使得螺旋桨在工作点处的雷诺数大于临界值3× 105，满足规程要求。桨叶雷诺数为

式中，ν为流体运动粘性系数。

敞水水动力的数值模拟结果见图3，图中试验结果为MSU给出的拖曳水池测试结果。

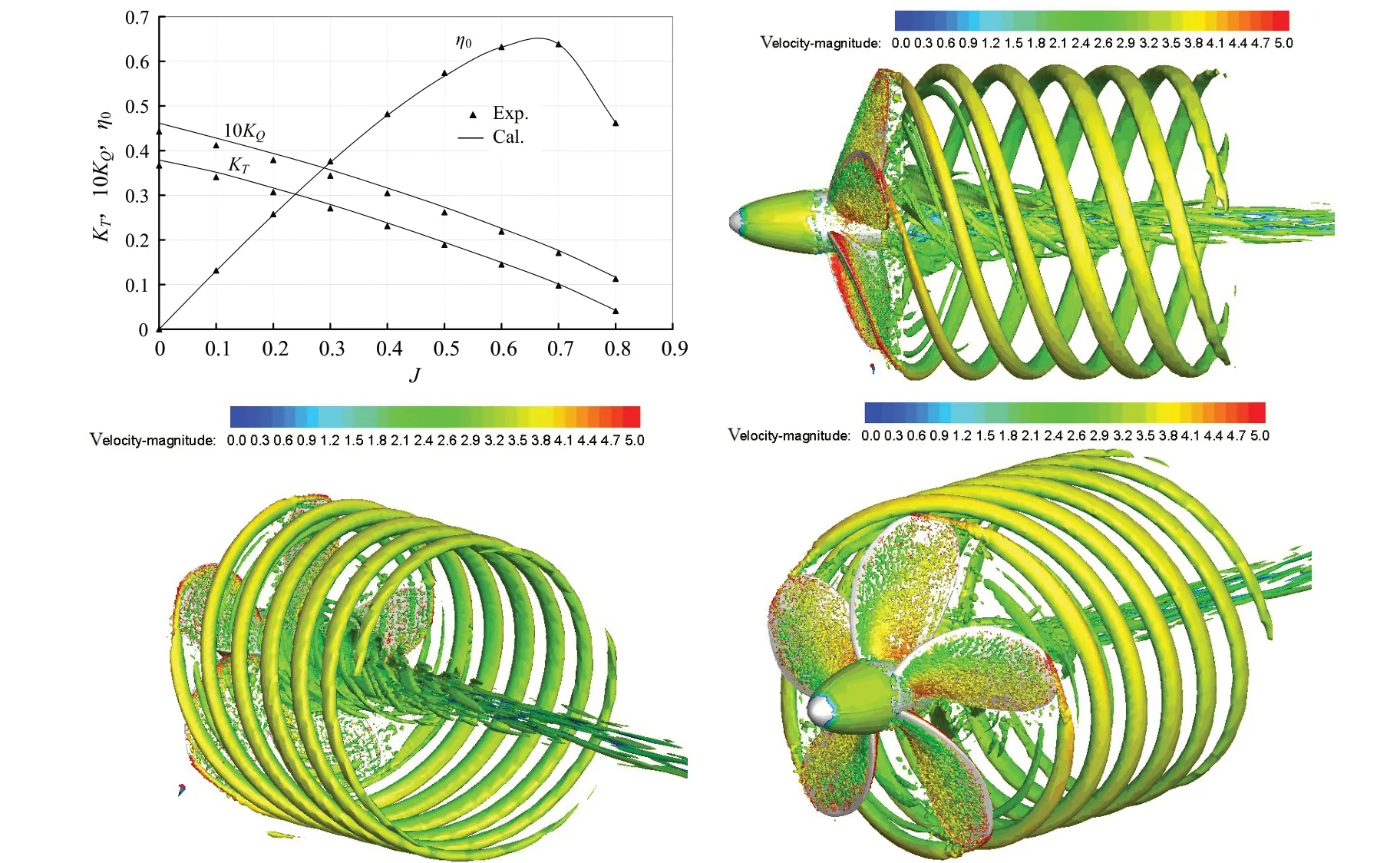
图3 敞水工况水动力与涡旋结构计算结果Fig.3 Computed hydrodynamic forces and vortical structures in open water condition

从图3可以看到，不同进速系数下，与试验结果相比，推力系数的计算误差为2%～3%，扭矩系数的计算误差为3%～4%，敞水效率的计算误差都为1%～2%。从工程预报角度来看，大涡模拟方法对螺旋桨敞水水动力（推力、扭矩）的预报达到了较高精度，计算效果是令人满意的。由于在大涡模拟方法中，网格比较精细，近壁面网格分辨率较优，可以直接解算到粘性底层，所以对于近壁面流动的计算效果较好，推力与扭矩的预报精度可以达到工程实用要求。

敞水工况下，J0= 0.7 时，螺旋桨周围的涡旋结构计算结果见图3，图中涡旋结构使用Q判据进行捕捉，Q判据的定义为

式中，ui、uj为三向速度，xi、xj为三向坐标。

从图3可以看到，在敞水工况，螺旋桨周围存在明显的梢涡、叶根涡。由于在敞水工况计算中，桨轴延伸至出口，所以毂涡汇入叶根涡中沿桨轴发展，传统意义上的毂涡计算结果见下面自航工况计算结果。梢涡以等螺距螺旋管形式向下游发展，由于螺旋桨对流动的抽吸加速作用，螺旋管所在的柱面直径略有减小。叶根涡的尺度较分散，但也以缠绕桨轴的螺旋管形式向下游发展。梢涡强度最高，形式最显著。

对于自航工况，采用与试验一致的等航速变转速强迫自航方法进行数值模拟。计算速度V选取为2.8～4.2 m/s，间隔为0.2 m/s。在每一自航速度下改变转速n（4～5 点），每次记录转速n、强制力z、桨推力TB、艇阻力R和桨扭矩QB，结合敞水数据分析自航因子，并对各个速度下的自航因子进行算术平均作为最终结果。通过自航计算可以得到如下的艇后螺旋桨水动力特征值。

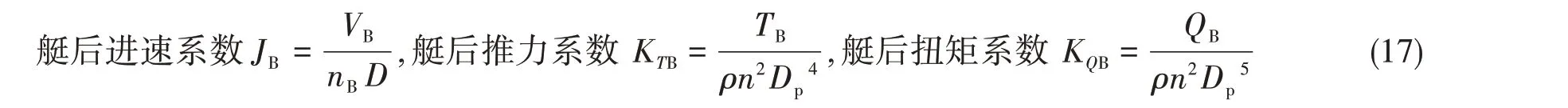
用等推力法按照艇后推力系数从敞水曲线上查得J0、KQ0，进而计算得到如下自航因子：

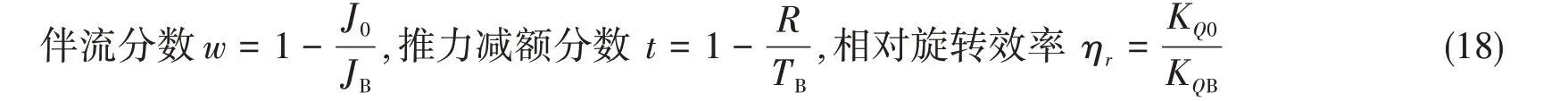
潜艇带桨自航状态尾部涡旋结构计算结果见图4。自航因子计算结果与试验结果的对比见图5，图中试验结果为美国UM给出的拖曳水池测试结果。

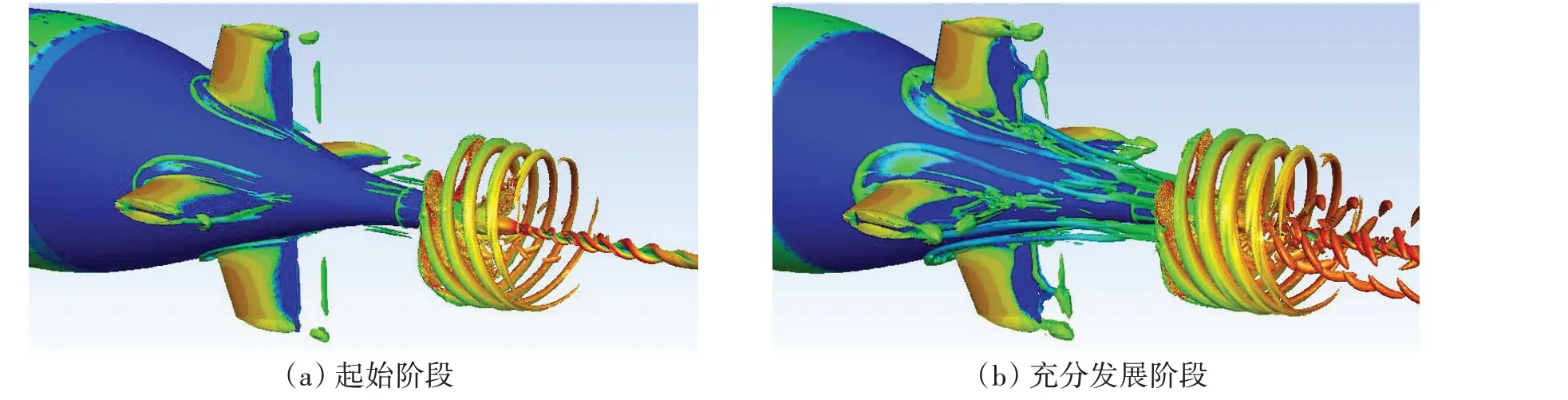
图4 潜艇自航工况尾部涡旋结构计算结果Fig.4 Computed vortical structures around the stern of submarine in self-propulsion condition

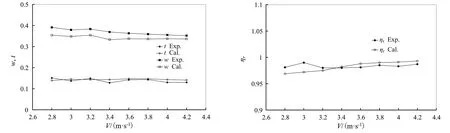
图5 自航因子计算结果与试验结果对比Fig.5 Comparison between computed results and measurements of self-propulsion factors

从图4 中可以看到潜艇自航工况下尾翼与螺旋桨周围涡旋结构的发展演化情况。图4 中左图为潜艇自航工况尾部涡旋结构的起始阶段，此时尾翼根部的马蹄涡刚出现不久，涡腿尚未充分发展，螺旋桨梢涡、毂涡都已出现，也在发展演化之中；右图为潜艇自航工况尾部涡旋结构的充分发展阶段，经过30 个旋转周期涡旋流场的发展演化后，尾翼根部马蹄涡、螺旋桨梢涡、毂涡、叶根涡都已达到成熟的形态。与敞水工况相比，螺旋桨周围同样存在明显的梢涡、叶根涡、毂涡，而且此时螺旋桨在潜艇尾部与尾翼不均匀来流相互作用，使得流动形式更为复杂。梢涡以等螺距螺旋管形式向下游发展，叶根涡非常明显，以离散螺旋形式向下游泄落，毂涡如同两股交替缠绕的水流相互作用，为双螺旋结构，稳定地向下游发展。梢涡强度最高，叶根涡与毂涡的形式也非常显著。

从图5 可以看出，与试验结果相比，推力减额的计算误差为2.8%～11.7%，伴流分数的计算误差为4.6%～9.5%，相对旋转效率的计算误差为1.2%～2.3%。可见大涡模拟方法对自航因子与艇后螺旋桨水动力（推力、扭矩）的预报达到了工程预报精度，计算效果是令人满意的。

3.2 螺旋桨噪声计算结果分析

朱锡清（2008）[26]对螺旋桨噪声的成因与种类进行了分析和阐释。当螺旋桨工作在非空泡状态，螺旋桨的噪声主要由离散谱（线谱）噪声、低频宽带噪声和中高频随边噪声组成。一般认为，离散谱噪声主要是由于螺旋桨工作在船艉的非均匀流场中，当螺旋桨叶片周期性旋转时，会和这非均匀流场相互作用产生非定常升力脉动，从而辐射出周期性的离散谱噪声。螺旋桨的低频宽带噪声是由于桨工作在船艉和附体形成的厚湍流边界层中，当这随机的湍流和螺旋桨叶片相互作用时就会引起叶片攻角的脉动，即形成沿叶片叶展方向的升力脉动，从而产生了低频宽带噪声。螺旋桨中高频宽带噪声主要是由叶片上产生的湍流边界层对流通过随边时发生散射引起的，因此也称为随边噪声。

本文采用Powell 涡声方程计算得到了AU5-65 螺旋桨敞水工况噪声与自航工况噪声。图6 给出了两个工况的典型计算结果，此时两种工况下来流水速都为4 m/s，桨轴转速为25 r/s。声学积分区域为一圆柱体，上游在桨盘面之前1倍桨径之处，下游在桨盘面之后5倍桨径之处，圆柱体直径为2倍桨径。在敞水与自航工况下螺旋桨旋转区域形式与网格数量完全相同，亦即由几何形式与网格数量造成的计算误差可以忽略。图6中的螺旋桨噪声结果为声压谱源级，试验结果为MSU 给出的1/3 Oct.水槽测试结果，已经扣除了尾翼噪声，为了展示低频线谱噪声，计算结果给出的是连续谱，水槽中的试验一般难以辨识低频线谱噪声。从图6中计算结果可以看出，无论是敞水工况，还是自航工况，在500 Hz以下的低频段都存在窄带线谱噪声，自航工况的线谱噪声更为明显，这主要是由SUBOFF 潜艇尾部带十字型尾翼造成的比较强烈的非均匀流场所致。由于轴频为25 Hz，螺旋桨为5叶桨，所以理论上的1阶叶频为125 Hz，2阶叶频为250 Hz，3阶叶频为375 Hz。数值计算得到的1阶叶频为125.8 Hz，2阶叶频为251.7 Hz，3 阶叶频为375.6 Hz，与理论分析结果非常吻合。在1 阶叶频处，螺旋桨自航工况噪声比敞水工况噪声增大23.6 dB；在2 阶叶频处，自航工况噪声比敞水工况噪声增大19.9 dB；在3 阶叶频处，自航工况噪声比敞水工况噪声增大18.4 dB。可见艇尾的三维非均匀入流对低频线谱噪声有明显影响。对于敞水工况，1阶线谱噪声比2阶大5.2 dB，2阶线谱噪声比3阶大2.4 dB；对于自航工况，1阶线谱噪声比2阶大8.9 dB，2阶线谱噪声比3阶大3.9 dB。计算结果从定性与定量两方面来看也都与理论分析结果比较吻合。从图6中的计算结果还可以看到，除了线谱噪声之外，还存在随频率逐渐衰减的宽带噪声，试验结果表明0.5～10 kHz自航工况噪声比敞水工况增大5.2～16.1 dB，数值计算所反映的差异与试验基本一致。在0.5～10 kHz 频段，螺旋桨噪声数值计算结果与试验差异为2.5～8.9 dB，从声压谱谱型和幅值来看，计算结果令人满意，可以满足工程设计中预报和优化选型互比的需求。

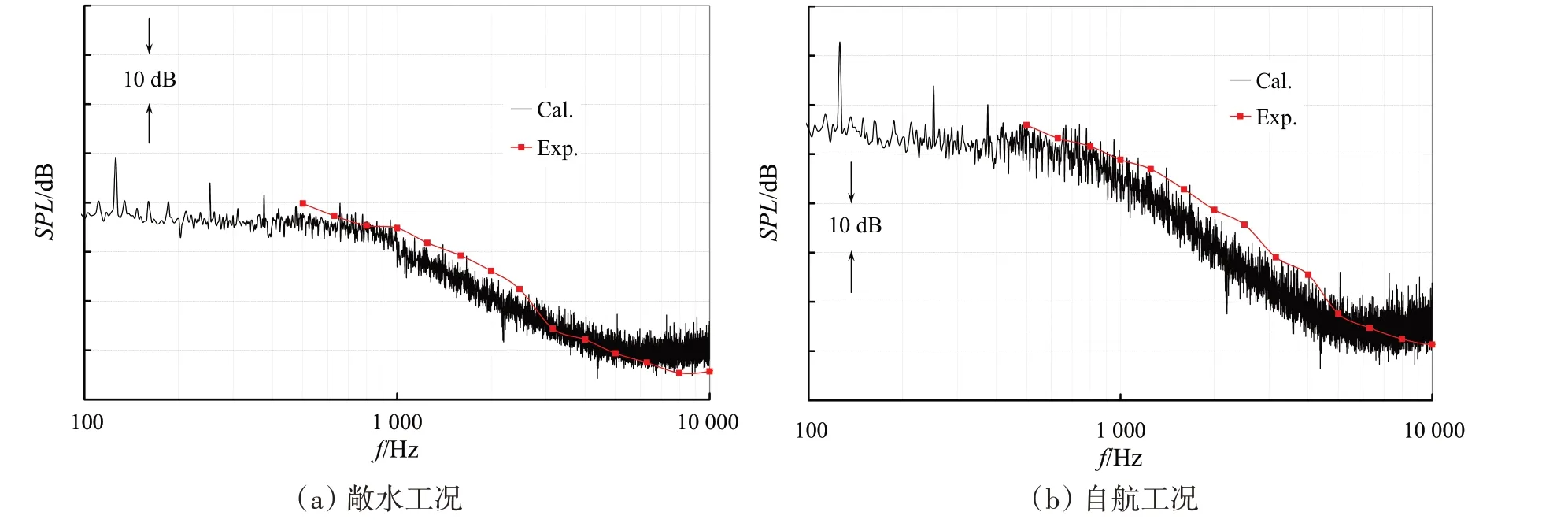
图6 螺旋桨噪声计算结果与试验对比Fig.6 Comparison of computed propeller noise with measurement

4 结 论

本文主要基于LES 结合Powell 涡声理论对于螺旋桨水动力与噪声数值预报方法进行了研究，阐释了Powell 涡声方程的物理内涵，给出了远场解的数学表达，对水动力与噪声计算结果进行了分析，并与试验结果进行了对比验证，证明了计算方法切实可行，计算结果可靠。将来可将此方法在螺旋桨工程初步设计与优化设计中加以应用，结合超级计算机并行计算技术，以减少试验巨大的工作量，为实用设计服务。本文得到的主要结论如下：

（1）基于LES 与Powell涡声理论的艇桨耦合状态螺旋桨水动力与噪声数值预报方法，计算过程稳定，计算效果好，具有工程实用价值，可在螺旋桨初步设计阶段以及优化阶段加以运用。该方法能同时求解出水动力和噪声，可为舰艇航速预报与噪声评估服务。

（2）不同进速系数下，与试验结果相比，敞水工况推力系数的计算误差为2%～3%，扭矩系数的计算误差为3%～4%，敞水效率的计算误差为1%～2%；自航工况推力减额的计算误差为2.8%～11.7%，伴流分数的计算误差为4.6%～9.5%，相对旋转效率的计算误差为1.2%～2.3%；在0.5～10 kHz频段，螺旋桨噪声数值计算结果与试验结果差异为2.5～8.9 dB。

（3）结合前期研究发现，使用上述计算方法时，流动涡旋结构的准确求解是正确计算流激噪声的关键，否则会产生较明显的虚假噪声。合理的亚格子涡模型与网格数量要经过系统的收敛性研究得到，对积分区域也要进行收敛性研究。流动计算时间一般要在30 个旋转周期以上，然后再开始噪声计算，噪声计算时间一般不小于30个旋转周期。

致谢：作者在螺旋桨噪声计算研究中得到了中国船舶科学研究中心朱锡清研究员的指教，在数值求解涡声方程方面得到了张效慈研究员的指教，在此向两位前辈表示衷心感谢！