基于Attention-ResNet-LSTM网络的中期负荷预测模型

刘新志 刘爱莲 李英娜

（昆明理工大学a.信息工程与自动化学院；b.云南省计算机技术应用重点实验室）

随着经济的发展和电力市场化的改革，我国电力需求量日益增加，这对于电力供需双方的平衡提出了更高的要求，因此精准的电力负荷预测极其重要［1］。 负荷预测依据时间长短可分为超短期、短期、中期、长期负荷预测［2］，这些负荷预测在电力系统中起着不同的作用，其中，中期负荷预测能很好地对电力系统的中期运行计划进行规划，减少供电中的运行成本，提高供电效率。 然而，目前关于中期负荷预测的研究很少，因此提高中期负荷预测精度具有重要的现实意义。

中期负荷预测方法包括时间序列法［3］、趋势外推法［4］、专家系统法［5］、小波分析法［6］、回归分析法［7］、灰 色 模 型［8］、人 工 神 经 网 络［9，10］及 组 合 预 测法［11］等。 文献［12］利用后验差检验优化GM（1，1）模型实现了中长期负荷预测；文献［13］将小波分析法与BPNN算法相结合应用在中期负荷预测中；文献［14］采用EMD与PSO-SVM相结合的方法实现了中期负荷预测。 以上方法存在的缺点是：没有考虑负荷数据的时序关系，而且无法很好地处理负荷数据与影响因素之间的关系。

深度学习是一种新的机器学习方法，它能很好地解决上述问题。 深度学习是利用隐藏层的多层感知器组成非线性网络结构，对海量数据进行预测。 循环神经网络（Recurrent Neural Network，RNN）模型在负荷预测中应用较多，文献［15］采用RNN模型对土耳其某地区的负荷进行预测；文献［16］将深度学习中的RNN与长短期记忆（Long Short-Term Memory，LSTM） 人工神经网络相结合用于预测不同单位住户的用电量。 然而，RNN对长周期时间序列持续的学习能力较弱。

在此， 笔者提出一种基于Attention-ResNet-LSTM网络的中期负荷预测模型。以爱尔兰某地区的真实负荷数据对该模型进行验证，并与RNN模型、LSTM模型和Attention-LSTM模型进行比较，以证明笔者所提模型的预测准确度及其适用性。

1 Attention-ResNet-LSTM网络

1.1 LSTM人工神经网络

LSTM人工神经网络是一种改进的循环神经网络［17］。 LSTM人工神经网络与RNN的结构［18］类似，均由输入层、隐藏层和输出层组成，但LSTM人工神经网络有着特殊的记忆单元结构 （图1），同时可以弥补RNN梯度下降的缺点。LSTM模型具有学习长期依赖的能力，能找出历史负荷数据与影响因素之间隐含的映射关系，故在长周期历史负荷数据预测中应用较多。

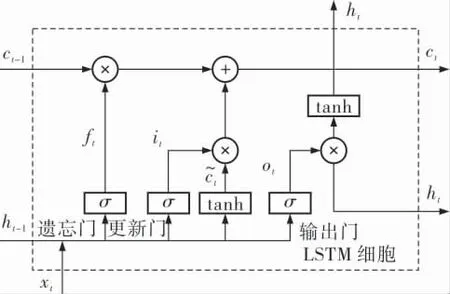
图1 LSTM记忆单元结构

ct——t时刻的单元状态；

c～t——t时刻候选的用来更新的细胞状态；

ht——t时刻神经元的输出量；

it——t时刻更新门的输出；

xt——t时刻输入的信息；

ft——t时刻遗忘门的输出；ot——t时刻输出门的输出；

σ——sigmoid激活函数

图1中LSTM模型采用3个“门”结构（遗忘门、更新门和输出门）来增强信息的传递与交流。 其中，遗忘门用来将上一时刻的单元状态选择性遗忘修正参数，更新门用来更新细胞的状态，输出门用来读取、输出和修正参数。

LSTM人工神经网络模型如下：

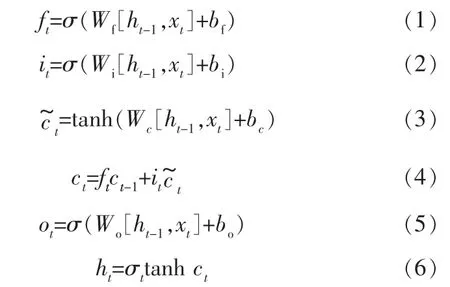
式中 b——偏置项；

c——更新后的细胞状态；

h——神经元的输出量；

W——权重；下角标 c——不同时刻的输入门输出的偏置项；

f——遗忘门；

i——更新门；

o——输出门。

1.2 Attention机制

Attention机制通过模拟人的大脑在某一时刻对大量信息中的某一信息分配更多的注意力，对其他信息关注很少甚至忽略，从而选出重要信息［19］。 笔者采用Attention机制对模型输入的特征向量赋予不同的权重， 从而找出更关键的因素，有助于模型进行精准的负荷预测。

在LSTM人工神经网络中加入Attention机制，找出影响负荷预测的重要因素， 提高预测精度。Attention单元如图2所示。

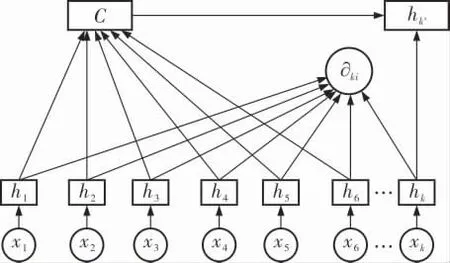
图2 Attention单元

图2中，x1，x2，…，xk为输入序列；h1，h2，…，hk为对应于输入序列的隐藏层的状态值；∂ki为历史输入信息的隐藏层对当前输入信息的注意力权重值；C为整个隐藏状态的一个加权；hk′为最后输出节点的隐藏层状态值。

Attention机制模型如下：

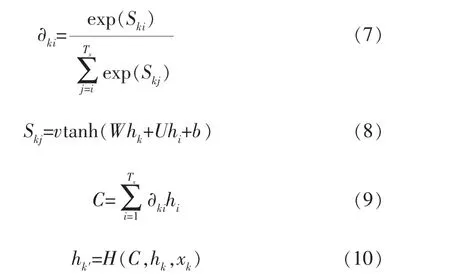
其中，Ski为i时刻隐藏层状态hi的能量值，Tx为输入信息的长度，v为输入的值，U、W为权重系数矩阵。

1.3 ResNet网络

ResNet是引入残差块而构建的深层网络［20］，深层网络构建要求叠加后的深层网络模型的误差低于基础的浅层模型。 ResNet可以减少信息损失并有效提高网络的收敛速度， 其结构如图3所示。

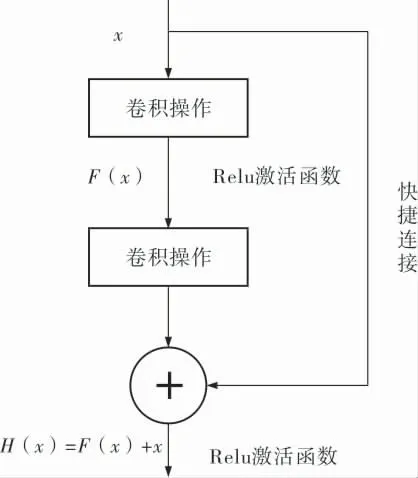
图3 ResNet网络结构

图3中，x为输入，F（x）为拟合残差映射，H（x）为输出，三者的映射关系为H（x）=F（x）+x。 计算F（x）=H（x）-x，若F（x）=0，则H（x）=x为一层叠加网络层后的最佳解映射；若F（x）≠0，但F（x）接近于0，则x逼近实际映射H（x）可以解决网络层堆叠的性能退化问题。

2 数据集及影响因素分析

2.1 数据集介绍

笔者选取的数据集为爱尔兰某地区2009年7月～2010年12月间201个工业用户536天的用电负荷数据， 其中包括一天内每隔15 min采集的电力负荷值及每天对应的气温变化、天气情况和当日信息（星期数）。 观察该地区用电负荷数据可以发现，工作日（星期一至星期五）耗电量较多，休息日（星期六和星期日）耗电量较少；冬季气温低（接近0 ℃），用电量较大，夏季气温在15～25 ℃，用电量相比冬季要小。

2.2 数据标准化

数据标准化采用min-max标准化法， 其计算式如下：maxmin

其中，xnorm为标准化后的值，xmax、xmin为数据中的最大值、最小值。

2.3 影响因素分析

分析数据集中的数据规律可知，日负荷以一周为单位呈周期性变化； 负荷受气温影响较大，气温下降，负荷量增加，气温升高，负荷量降低；冬季多阴雨天气，用电量增加。 因此，初步选取气温、天气情况和当日信息（星期数）作为影响因素。

首先将文字形式的影响因素做数值化处理，包括天气情况和当日信息（星期数）。 其中，天气情况的数值化规则见表1，当日信息（星期数）的数值化规则见表2。

表1 天气情况的数值化规则

表2 当日信息（星期数）的数值化规则

皮尔逊系数是一种计算直线相关性的方法，为此笔者采用皮尔逊系数对影响负荷的各个因素做进一步分析。 设两个变量分别为X、Y，则X与Y之间的关联性可以用皮尔逊系数ρX，Y表示：

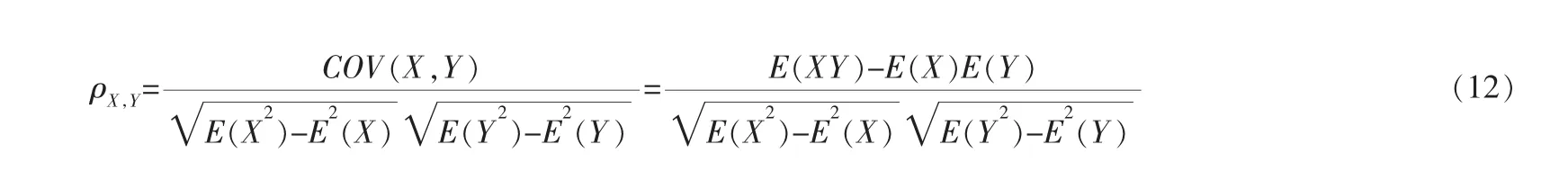
其中，E是数学期望，COV是协方差。

皮尔逊系数的值越接近1或-1， 相关程度越强；皮尔逊系数越接近0，相关程度越弱。 表3为相关系数范围，表4为各影响因素的相关分析结果。

表3 相关系数范围

表4 各影响因素的相关分析结果

分析表3、4可知：当日信息（星期数）、最高气温、最低气温与电力负荷呈负相关关系（中等程度相关）， 天气与电力负荷呈正相关关系 （弱相关）。

对当日信息（星期数）采用二进制进行数值化， 星期一至星期日的二进制形式分别为001、010、011、100、101、110、111。 采用独特的编码方法对天气进行数值化处理，即在任意时刻，只能取一位表示有效位，其余均为0，则天气因素的8种形式为：晴天10000000、多云01000000、雾天00100000、小 雨00010000、中 雨00001000、大 雨00000100、雨夹雪00000010、小雪00000001。 对于气温，通常采用分段函数进行处理，计算式如下：

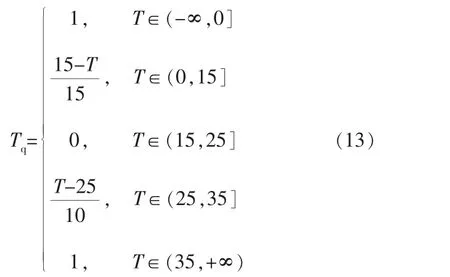
其中，Tq为量化后的温度，T为实际温度。

3 基于Attention-ResNet-LSTM网络的中期负荷预测模型

3.1 Attention-ResNet-LSTM网络结构设计

基于Attention-ResNet-LSTM网络的中期负荷预测模型（图4）对长周期、非线性时序数据持续学习能力较强，能很好地对长周期、非线性负荷做出预测。

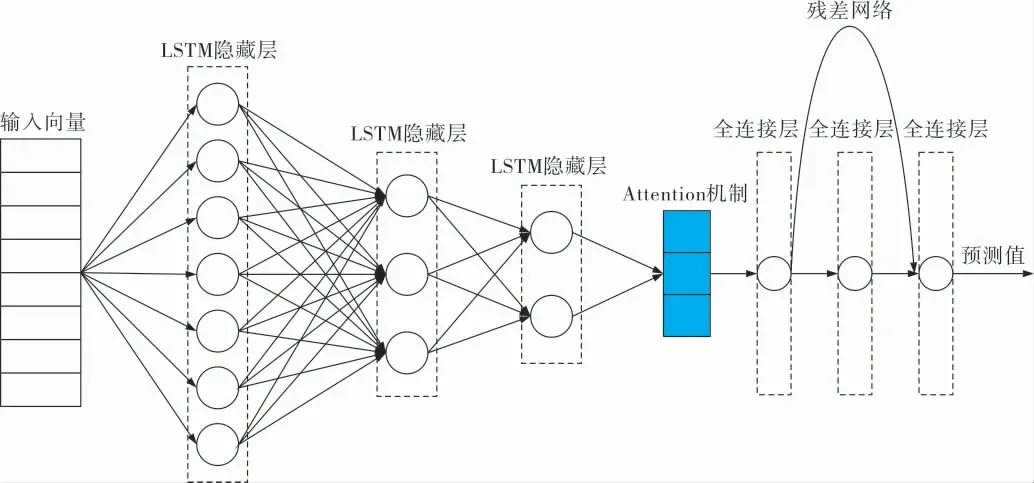
图4 基于Attention-ResNet-LSTM网络的中期负荷预测模型

在Attention-ResNet-LSTM模型中， 取历史日负荷数据L、当日信息（星期数）D、气温R和天气情况W作为特征向量X={LT，DT，RT，WT}进行输入，迭代1 000次，学习速率0.001，采用sigmoid函数作为激活函数。 表5为不同隐藏层层数的LSTM预测误差，可见，在最大迭代次数一致的前提下，随着隐藏层层数的增多，均方根误差RSME呈下降趋势，当层数增加到3时，RMSE=2.524 MW，运算时间为826 s，相较第2层的运算时间（771 s）只增加了55 s；当层数增加到4时，RSME呈上升趋势并开始出现过拟合现象。 综合考虑后，笔者采用3层隐藏层的LSTM人工神经网络。

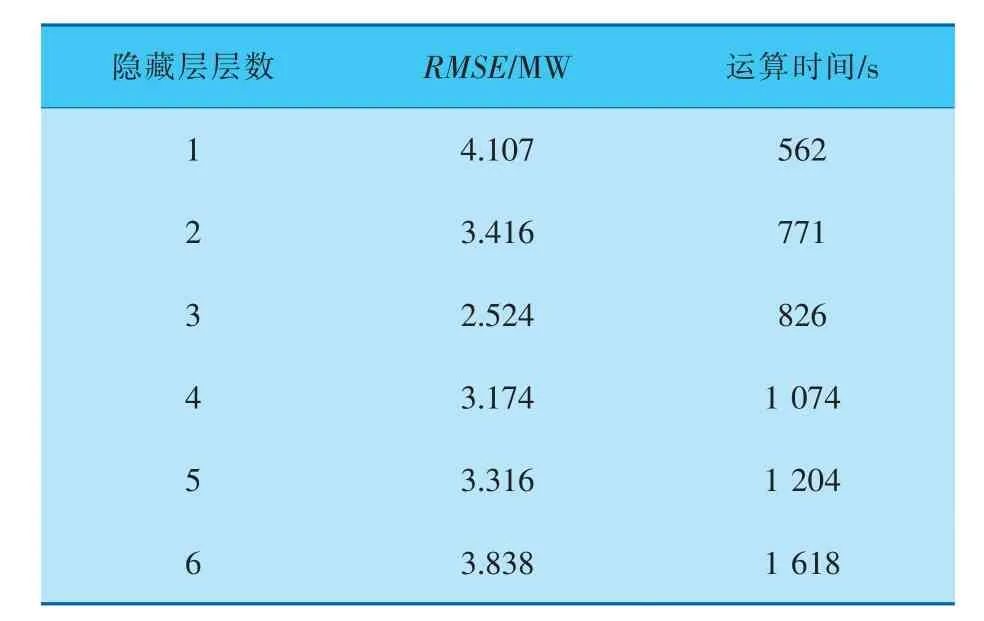
表5 不同隐藏层层数的LSTM预测误差

LSTM各层神经元的个数一般为2的N次方数， 若第1层神经元个数过少， 则会降低学习效果。 为了保证数据流的体积变小，层与层之间神经元的数量应依次递减，这样可以解决当输入数据增多时全连接层之间的参数成倍增加的问题。表6为3层隐藏层情况下不同神经元个数LSTM的预测误差。 在方案1中，3层隐藏层的神经元个数分别为8、4、2，总数14，以后每个方案中的神经元总个数以2的倍数递增。 纵观5个方案， 方案4的RMSE=2.524 MW， 运算时间为826 s， 为综合最佳，此时每层神经元的个数分别为64、32、16。

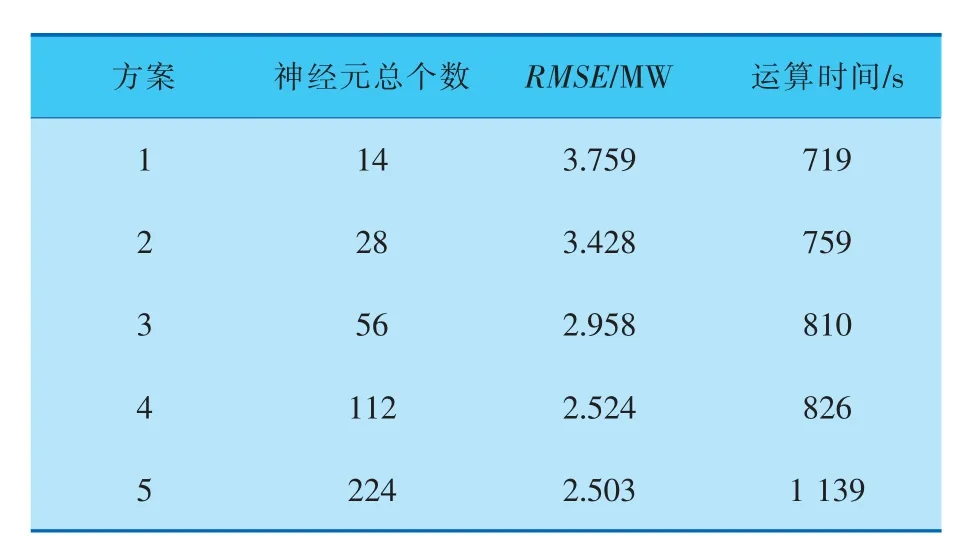
表6 3层隐藏层情况下不同神经元个数LSTM的预测误差

3.2 评价指标

采用平均绝对百分比误差 （Mean Absolute Percentage Error，MAPE）和均方根误差RMSE作为预测结果的评价指标，两者的计算式分别如下：

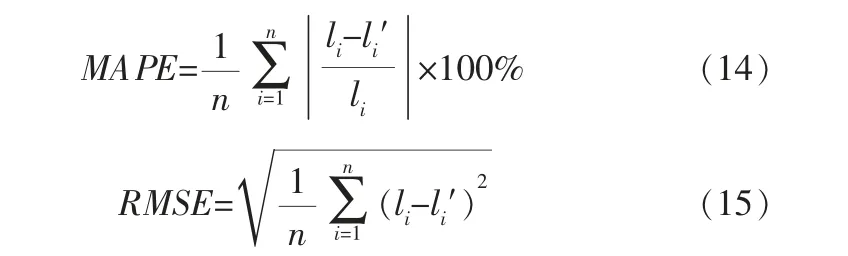
其中，n为预测点的个数，li为第i个点的实际负荷，li′为第i个点的预测负荷。

3.3 算例分析

选择爱尔兰某地区某代表工业用户2009年7月～2010年11月的真实负荷为训练集，2010年12月的真实负荷为测试集， 采用Attention-ResNet-LSTM模型对2010年12月的负荷做出预测， 并与LSTM模型、RNN模型和Attention-LSTM模型进行对比（表7）。 通过表7可以得出，Attention-ResNet-LSTM 模 型 的MAPE=1.724% ， 相 比Attention-LSTM、LSTM、RNN 分别减少了1.440%、4.059%、6.339%；MAPE与RMSE越小， 则说明该模型的预测精度越高， 可见在4种模型中Attention-ResNet-LSTM模型的预测精度最高。

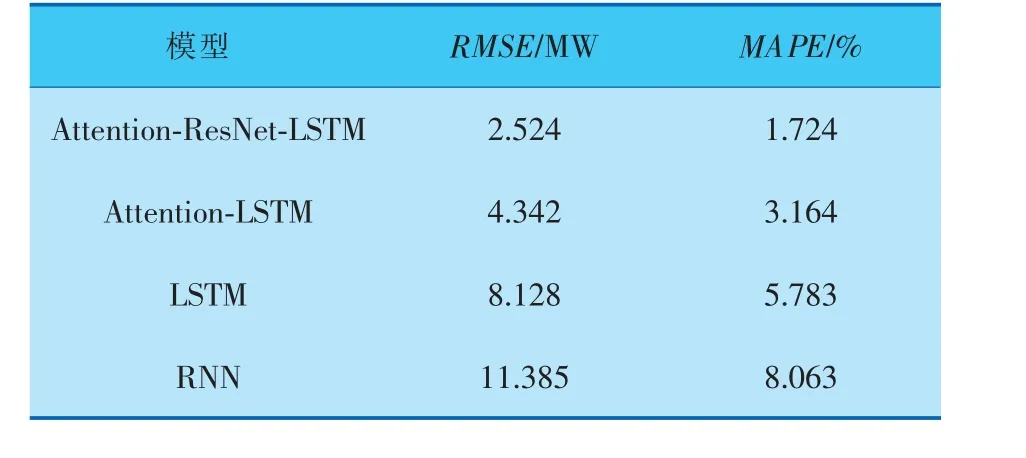
表7 4种模型预测结果的评价指标对比

图5为采用4种模型对2010年12月负荷的预测结果与真实负荷的对比。 可以看出：Attention-ResNet-LSTM模型的预测结果与真实负荷的拟合程度最好，说明该模型有着更好的适用性，更适用于对中期负荷的预测。

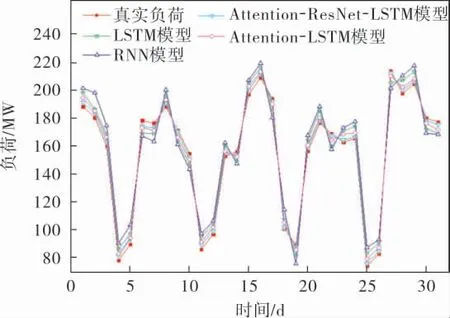
图5 4种模型的负荷预测结果与真实负荷的对比

4 结束语

针对电力负荷的周期性、时序性、非线性特性以及负荷预测影响因素众多的问题，笔者提出了一种基于Attention-ResNet-LSTM网络的中期负荷预测模型， 其中Attention机制突出重要影响因素，ResNet网络减少信息损失和提高模型的收敛性。 以爱尔兰某地区的真实负荷为数据集进行仿真实验， 对一个月的负荷进行预测， 结果表明，Attention-ResNet-LSTM模型的MAPE=1.724%，比RNN、LSTM、Attention-LSTM模型的预测精度高，证明了该模型的有效性和精准性。 在实际的电力负荷预测中，Attention-ResNet-LSTM中期负荷预测模型具有一定的借鉴意义。