基于参数优化VMD 的滚动轴承故障诊断方法

彭康健，陈君若，吴智恒

（650500 云南省 昆明市 昆明理工大学 机电工程学院）

0 引言

滚动轴承作为机械设备中的重要零部件，对于机械设备的运行起着至关重要的作用，据统计，在使用滚动轴承的机械设备中，约有30%的机械故障是由轴承故障而引起的[1]。作为机械设备中的重要零部件，一旦发生故障，不仅会影响其正常运行，还可能给企业带来巨大的经济上的损失甚至安全问题[2-3]。因此滚动轴承的状态监测和故障诊断具有重要的现实研究意义。

轴承故障诊断过程大致可分为信号采集、特征提取、故障识别和诊断分析4 个步骤，其中特征提取可以说是故障诊断过程中最关键的一步。常用滚动轴承故障特征提取的方法是，先通过传感器采集轴承的振动信号，这些振动信号与设备的运行状态直接相关，但由于采集的信号通常是非线性、非平稳的，所以并不能直接提取故障特征[4]。于是一些信号时频分析方法应运而生，并对设备的监测监控有着重大现实意义[5]。目前常用的时频分析方法有：Huang[6]等人提出的经验模态分解（Empircial Mode Decomposition）方法；Smith[7]提出的一种针对非线性非平稳信号的局部均值分解（Local Mean Decomposition）方法；以及Wu[8]等又在现有经验模态分解方法基础上提出的集合经验模态分解（Ensemble Empirical Mode Decomposition）方法。上述方法都在轴承故障诊断分析中取得了良好的效果，但也有着各自的局限性与不足。比如EMD 方法缺少严谨的数学基础，容易产生模态混叠和端点效应；LMD 方法计算量大，可能产生由解调引起的信号突变问题。而变分模态分解方法作为一种相对成熟的算法，目前在轴承故障诊断领域有着不错的效果。

变分模态分解方法作为一种自适应信号处理方法有着较为成熟的理论基础，于2014 年由Dragomiretskiy 等人提出[9]。该方法通过迭代搜索变分模型的最优解来确定各个分量的频率中心和带宽，从而有效地获取模态分量，自适应地完成轴承信号的频域及各分量的有效分离。相对于传统EMD 方法，该方法有着良好的数学理论支撑，同时有着较好的抗噪性和自适应性，避免了递归模式分解造成的包络线估计误差不断累积，克服了端点效应[10]。

本文针对变分模态分解中的模态数K 和惩罚因子α两个参数的取值，通过熵最小值的方法确定最佳参数组合[K，α]。然后对信号进行变分模态分解，得到了K 个IMF 分量，选取包络熵最小的IMF 分量，对其IMF 分量进行包络解调分析，从而提取轴承故障特征频率信息。

1 变分模态分解

变分模态分解（Variational Mode Decomposition，VMD）是基于维纳滤波的自适应信号处理方法，它把信号分解成一系列固有模态分量（Intrinsic Modal Function，IMF），每个IMF 分量表示为

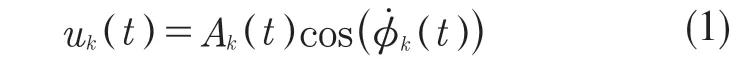
式中：Ak（t）——uk（t）的瞬时幅值；ωk（t）——uk（t）的瞬时频率，ωk（t）=φk'（t）=dφk/dt。

对于方法变分模型，假设信号被分解成K 个模态分量（IMF），每个模态分量uk(t)都紧密围绕在一个确定的中心频率ωk（t）周围，对于一个一维信号f，确定其模态分量uk（t）的频带范围的算法过程如下：

（1）通过希尔伯特变换方法得到与各个模态分量uk（t）相应的解析信号，从而获得其单边频谱。

（2）加入指数项调整各自估计的中心频率，将每个模态分量的频谱调制到基频带上。

（3）通过H1高斯平滑估计解调信号的带宽，即计算其梯度二范数的平方。变分问题就变成了寻找K 个模态分量uk（t），并使所有模态分量估计带宽最小的问题。设原始信号经过变分模态分解后的分量数为K，则约束变分模型为

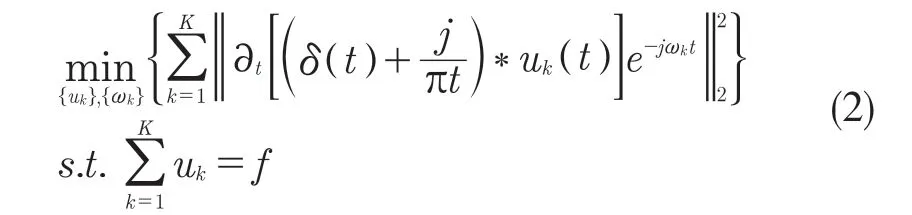
式中：{uk}={u1，u1，…，uk}——分解后的k 个模态分量；{ωk}={ω1，ω1，…，ωk}——各模态分量的频率中心；δ——狄拉克分布；t——时间；*——卷积；k 越大表示的频率成分越低。

为确保信号的绝对可积性，这里引入一个二次惩罚因子和增广 Lagrange 函数，即

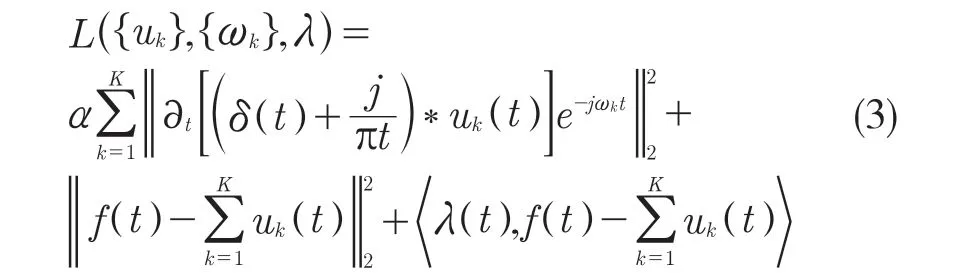
式中：∂——惩罚因子；λ——Lagrange 乘子。

根据上述理论，VMD 计算流程如下：

Step2：n=n+1,执行循环程序；

Step3：更新{uk}，{ωk}；

Step4：k=k+1，重复step3，直到k=K；

Step5：更新λn+1=λn+τ（f-∑ukn+1）；

Step6：设置判别精度ε，直到满足迭代停止条件，结束循环，得到K 个模态分量输出。

2 鲸鱼优化算法

鲸鱼优化算法[11]是一种启发式算法，具有简单易实现、能有效避免局部最优、可扩展性好等优点。目前对于变分模态分解参数优化已经使用的优化算法有：遗传算法[12]、果蝇优化算法、蝙蝠优化算法、粒子群优化算法[13]等。而鲸鱼优化算法相比于以上几种算法有原理简单、易于实现、调整参数少以及鲁棒性强等优点。

鲸鱼算法的原理主要模拟座头鲸的捕食行为，这种较为独特的捕食行为被叫作泡泡网觅食法，如图1 所示。

图1 鲸鱼捕食图Fig.1 Whale hunting map

鲸鱼优化算法的过程主要包括随机搜寻食物、包围捕食和气泡捕食3 个阶段。其捕食过程的数学模型如下：

2.1 鲸鱼的包围捕食

鲸鱼捕食过程中，先观察和寻找猎物的位置，然后对猎物进行包围。假设待优化的问题解及问题变量为最优的鲸鱼所在的位置，其他鲸鱼也会朝向该鲸鱼的位置移动从而更新自身的位置，所以要求的是个体与最优鲸鱼位置（猎物）之间的距离

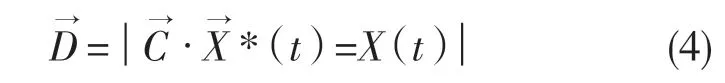
鲸鱼根据最优鲸鱼的位置更新而更新

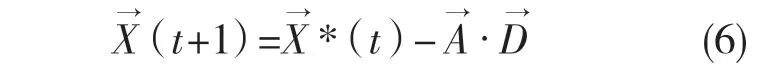
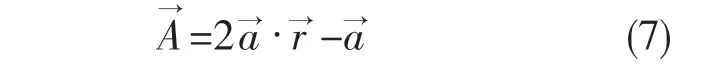
2.2 鲸鱼的气泡捕食阶段

鲸鱼的气泡捕食阶段分为两种方式：

（1）摇摆包围捕食

（2）螺旋吐气泡捕食

此阶段中，鲸鱼首先计算出自身到猎物（当前为止最好的位置）之间的距离，然后鲸鱼会在以螺旋形姿势向上游动的过程中吐出大小不等的气泡捕食鱼虾。该行为的数学模型如下：

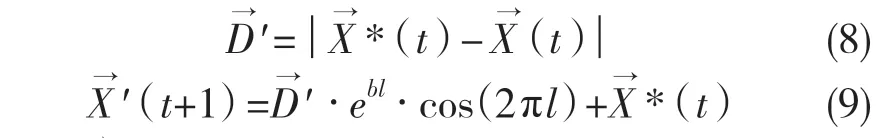
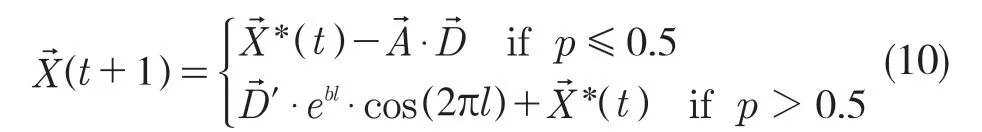
式中：p——[0，1]之间的随机数。鲸鱼的捕食行为除了气泡捕食方法外，还会随机寻找视野范围内的猎物，该行为为鲸鱼的全局搜索。

然而，鲸鱼在捕食过程中会随着其他鲸鱼位置改变而更新自身位置，也就是说此阶段的鲸鱼不再随着最好的鲸鱼的位置更新自身位置，而是大范围地随机搜索猎物，因此算法是随着收敛因子A 的变化而进行更大范围的搜索过程。当 A>1时，鲸鱼将进行随机搜索猎物的行为，这样可以避免陷入局部最优的情况，其数学表达式如下：

（1）初始化参数：鲸鱼的种群规模X、最大迭代次数Tmax，初始化鲸鱼种群位置；

（2）计算各鲸鱼的适应度值，并确定当前最优鲸鱼个体X*；

（3）进入算法主循环，如果p<0.5 且|A1|<1，每只鲸鱼个体按照式（6）更新当前位置，否则按照式（12）更新鲸鱼个体位置。如果p ≥5.0，则每只鲸鱼个体依据式（9）更新位置；

（4）再次对整个鲸鱼种群进行评价，找到全局最优的鲸鱼个体及其位置；

（5）若满足算法的终止条件(最大迭代次数)，则结束；否则转到步骤（2），继续进行算法迭代。

（6）输出全局最优解*X 。

3 基于VMD 的轴承故障特征提取方法

VMD 分解过程中的模态分量K 和惩罚因子α的选取直接关系着VMD 的分解效果。如果分量个数K 取值过小，可能造成模态混叠的现象；K 值过大，分解的结果中就可能产生虚假分量，不利于分析。而二次惩罚因子α的取值越小，则分解后的各IMF 分量的带宽越大；反之，α越大，则各个IMF 分量的带宽越小。所以，选择适当的K、α值对VMD 分解效果非常重要。

对于优化问题，首先需要设定一个适应度函数，以此函数来确定最佳参数。故使用鲸鱼优化算法对VMD 进行参数优化时，需设定一个适应度函数来进行迭代寻优，确定VMD 的最佳参数组合。文献[3]提出了包络熵的概念，包络熵反映了信号的稀疏特性，若信号经过VMD 分解后IMF 分量中含有较多的周期性故障冲击信息时，则其稀疏特性强，包络熵值小；反之，如果分解后IMF 分量中只有较少的周期性故障冲击信息时，则其稀疏特性弱，包络熵值大。本文中将VMD 分解后的局部极小包络熵作为鲸鱼优化算法中的适应度函数，搜寻最优的VMD 参数组合[k，α],即模态分量个数和二次惩罚因子。包络熵Ep的计算公式为

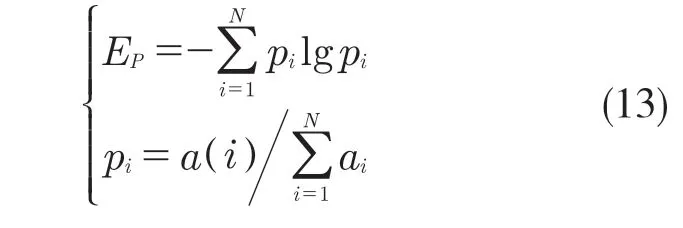
式中：pi——a（i）的归一化形式；a（i）——信号x（i）经Hilbert 解调后得到的包络信号。

鲸鱼算法优化VMD 参数步骤：

（1）确定适应度函数，设鲸鱼个体的解为（α，K），初始化算法参数；

（2）将信号进行VMD 过程得到各个 IMF，根据式子计算每个 IMF 的包络熵；

（3）将最小包络熵值作为适应度函数进行全局搜索；

（4）根据式（6）、式（12）更新鲸鱼个体的位置；

（5）重复步骤（3）至步骤（5），只要达到包络熵值最小或者达到设定的最大迭代次数，则输出最佳参数组合个体（α，K）；

（6）设置最优参数（α，K）组合对信号进行 VMD 分解。

表1 中：X——鲸鱼的种群规模；Tmax——最大迭代次数；Lb——分解层数K 和惩罚系数alpha的下限；Ub——分解层数K 和惩罚系数alpha 的下限和上限。判别精度设置为1×10-6。

表1 鲸鱼算法各参数设置Tab.1 Each parameter setting of whale algorithm

如图2 所示，对于轴承信号处理，首先是获取原始信号，对原始信号进行鲸鱼算法优化确定VMD 相关参数组合（α，k），然后将信号进行VMD 分解后得到各IMF 分量，并选择最佳模态分量进行包络谱分析，得到故障特征频率，从而判别故障类型，实现故障诊断。

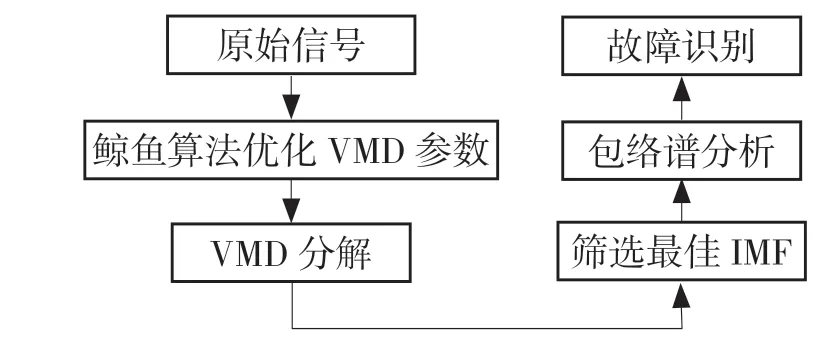
图2 轴承故障诊断步骤Fig.2 Step of bearing fault diagnosis

4 实验验证

采用美国西储大学滚动轴承故障模拟实验台的公开数据进行分析验证。实验轴承安装在电机转轴两侧，其中一端为驱动端，另一端为风扇端。这里选用的待测轴承安装在转速为 1 797 r/min 驱动端轴承SKF6205，采样频率为12 kHz；

表2 6205-2RS JEM SKF 深沟球轴承Tab.2 6205-2RS JEM SKF deep groove bearing

其中：2RS 表示双面密封，SKF（Svenska Kullager-Fabriken）为斯凯孚公司，轴承滚动体个数为9 个，轴承的故障类型为电火花加工的单点损伤，损伤直径0.177 8 mm。

根据公式计算得轴承理论的外圈、内圈、故障特征频率分别为：BPO=107.3 Hz、BPI=162.1 Hz，实测信号的时域波形图如图3、图4 所示。

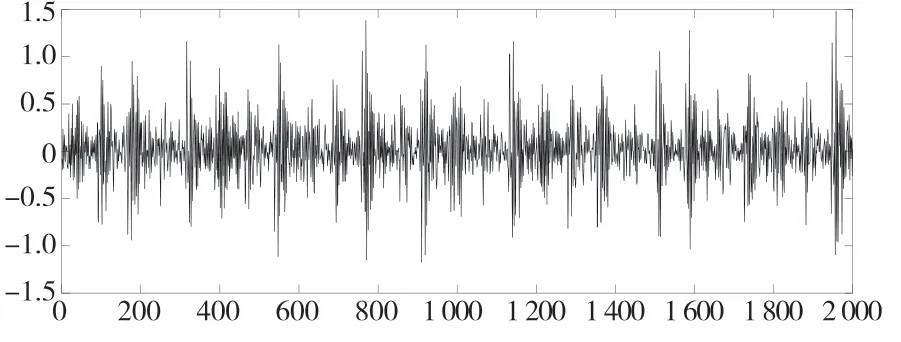
图3 滚动轴承内圈时域波形图Fig.3 Time domain waveform of inner ring of rolling bearing

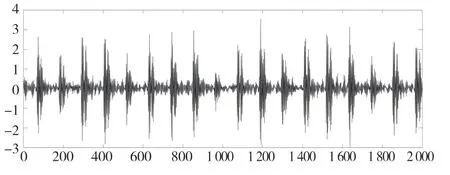
图4 滚动轴承外圈时域波形图Fig.4 Time domain waveform of moving bearing outer ring

将上述轴承信号加载至MATLAB2020a 中，以最小包络熵为适应度函数，使用鲸鱼算法优化变分模态的α，K 值。由图5、图6 可以得到：对于内圈故障，当群体进化代数到第11 代时得到了局部极小熵值4.887；对于外圈故障，当群体进化代数到5 代时得到了局部极小熵值4.914。于是可分别得到最佳α，K 组合：内圈为 alpha= 1 880，K=4；外圈为alpha=2 596，K=6。

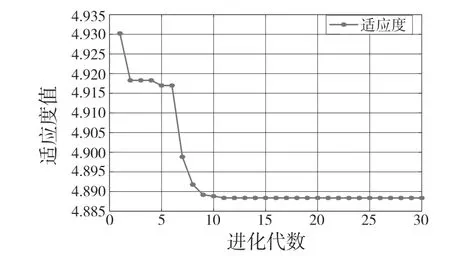
图5 鲸鱼算法优化值随进化代数的变化曲线（内圈故障）Fig.5 Curve of optimal value of whale algorithm with evolutionary algebra (inner)

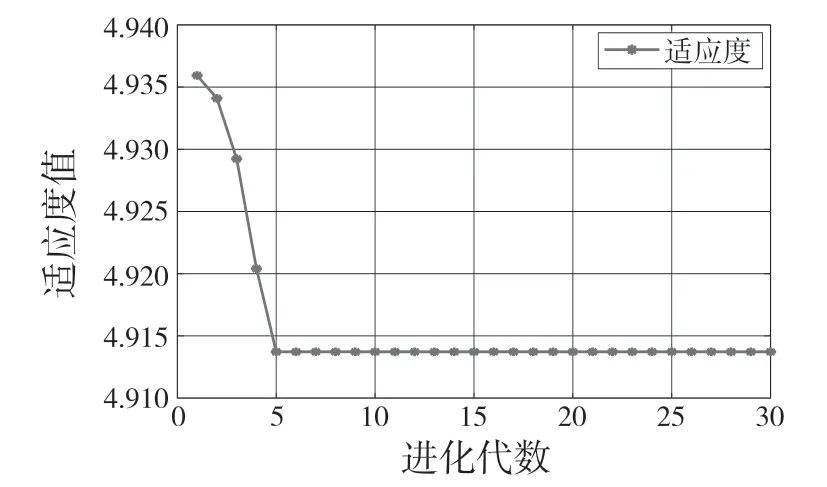
图6 鲸鱼算法优化值随进化代数的变化曲线（外圈故障）Fig.6 Curve of optimal value of whale algorithm with evolutionary algebra (outer)

确定参数后，分别对两种故障的振动信号进行变分模态分解和频谱、包络谱分析，分别如图7—图9 所示，图10 为最佳模态分量包络谱。

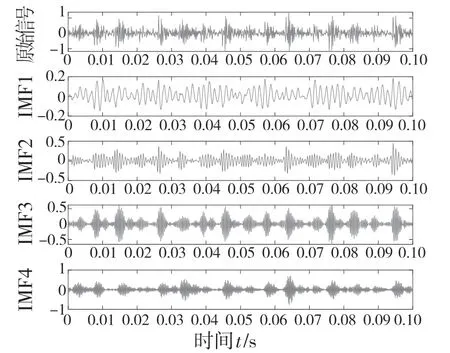
图7 模态分量IMF1-IMF4Fig.7 Modal component IMF1-IMF4

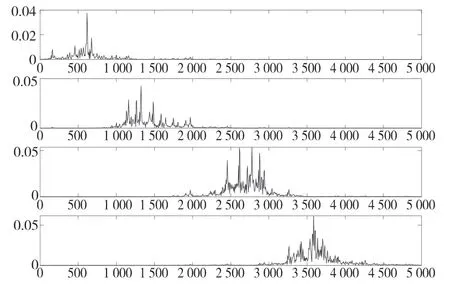
图8 模态频谱Fig.8 Modal frequency spectrum

图9 IMF1-IMF4 分量包络谱Fig.9 IMF1-IMF4 envelope spectrum

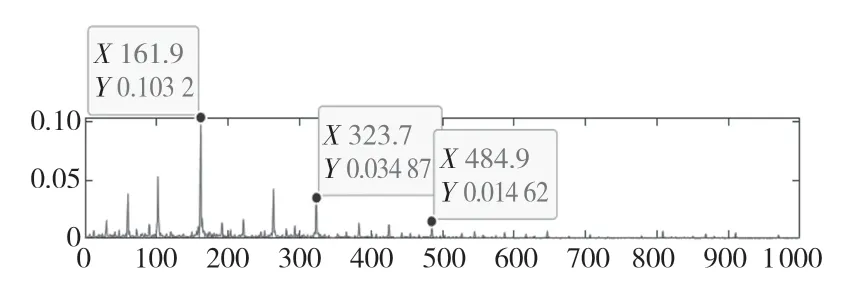
图10 最佳模态分量IMF4 包络谱Fig.10 The best component IMF4 envelope spectrum

外圈故障VMD分解各模态分量如图11所示，图12 为最佳模态分量。

图11 IMF1-IMF4 分量包络谱Fig.11 IMF1-IMF4 envelope spectrum

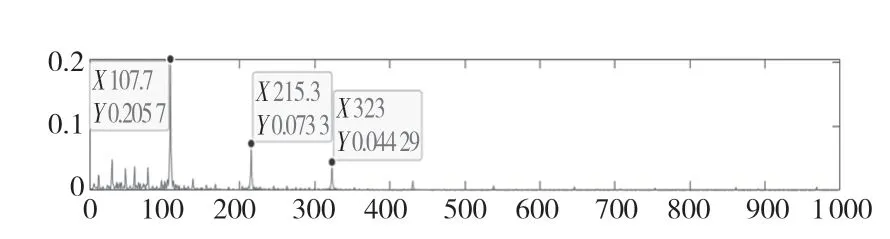
图12 最佳IMF 分量Fig.12 Best IMF

由频谱图可见，轴承转频为60 Hz，各种类型的故障频率161.9，107.7 Hz分别对应轴承内圈、外圈的理论故障特征频率162.1，107.3 Hz。

同样，对内外圈轴承振动信号进行EMD 分解，对于同样的故障振动信号，对于内圈故障，当EMD 分解到IMF5 时，就基本看不到故障特征频率了；对于外圈故障，当EMD 分解到IMF6 时，就基本看不到故障特征频率了。在这里我们取有效的IMF 分量进行频谱分析，从图10 和图13、图12 和图14 中IMF 分量进行对比可以看出，VMD 分解最佳分量相对EMD 分解分量幅值更大，故障特征频率相对更加明显。

图13 内圈EMD 分解IMF1-IMF4Fig.13 Inner EMD IMF1-IMF4

图14 外圈EMD 分解IMF1-IMF5Fig.14 Outer EMD IMF1-IMF5

5 结论

VMD 方法作为一种有着良好数学理论支撑的自适应分解算法，能够有效改善信号分解过程中的模态混叠与端点效应问题，对非平稳非线性的信号的故障特征频率的提取有着良好的处理效果。本文针对VMD 算法中参数 K与α的取值问题，提出了基于最小包络熵的鲸鱼算法优化方法，并证明该方法能够较为有效地得到参数 K 与α的取值并得到较好分解效果。通过与EMD 方法进行实验对比，表明该方法相比EMD 方法更能突出故障特征频率，从而判别故障类型。

但是该方法也存在以下不足：（1）算法参数选取经验性较强，在优化过程中可能存在优化结果不稳定，当迭代次数过大时也存在运行时间长的问题；（2）除K 和α值外，对于VMD 的其他参数的设定也有待研究。