基于VMD-ELM的锂离子电池剩余寿命预测方法研究
2021-11-26邹博雨张营李泱陈璐徐剑澜顾杰
邹博雨,张营,李泱,陈璐,徐剑澜,顾杰
(210037 江苏省 南京市 南京林业大学 汽车与交通工程学院)
0 引言
锂离子电池是一种能量密度大、输出电压高、循环性能优越的绿色电池,被广泛应用于航空航天、国防军事等领域,是诸多领域重要的支撑环节,因此对于锂离子电池进行健康管理显得尤为重要[1]。随着电池使用时间的增加,会导致电池容量出现逐渐衰退的情况,因此可利用锂电池的容量表征锂电池的退化特性[2],并基于此对剩余寿命(Remaining Useful Life,RUL)进行预测。
目前,锂离子电池剩余寿命预测方法主要有基于模型的预测方法和基于数据驱动的预测方法[3]。基于模型的预测方法按锂电池内部的结构特性,建立表征退化的模型,但由于电池内部结构复杂模型难以建立;基于数据驱动的预测方法不依赖于电池内部结构,采用机器学习的方法对电池退化特征参数的性能退化规律进行挖掘,实现RUL[4]。常见的基于数据驱动的预测方法包括神经网络[5-6]、支持向量机[7-8]、相关向量机[9-10]、高斯过程回归[11-12]等。其中,极限学习机(Extreme Learning Machine,ELM)是单隐层神经网络,不仅可以很好地避免传统的基于梯度下降算法神经网络调节参数多、易陷入局部最优解等麻烦,而且克服了以支持向量机为代表的一类算法在不确定性表达方面的缺陷[13],具有高泛化性、计算复杂度低、训练速度快等优点[14]。
锂离子电池的容量衰退是一个非线性退化过程,直接利用非线性退化信号进行建模预测精度低。因此基于信号分解和预测模型的方法被用于提高预测精度[15]。常用信号分解方法包括经验模态分 解(Empirical Mode Decomposition,EMD)[16]、集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)[17]、局部均值分解(Local Mean Decomposition,LMD)[18]等。变分模态分解[19]是一种新型的信号分解方法,其整体框架是变分问题,将非平稳信号分解为数个有限带宽的模态分量。相比常用的EMD,VMD 将信号分解转化为非递归、变分模态分解模式,表现出更好的鲁棒性,同时通过收敛条件的合理控制,使其分量个数也小于EMD。
针对锂离子电池的容量衰退是一个非线性退化过程,剩余寿命精确预测困难的问题。本文提出一种基于VMD 和ELM 的锂离子电池剩余寿命预测方法。利用VMD 分解锂电池容量信号得到一系列表征信号局部特性的IMFs,然后基于每个IMF,分别训练ELM 模型。最后将每个ELM 模型的预测结果加和求得锂离子电池的剩余寿命。
1 变分模态分解(VMD)
变分模态分解的分解过程是变分问题的求解过程[19],该方法是Dragomiretskiy 在2014 年提出的信号处理方法,可以将由多种频率组成的信号优化为数个有限带宽的固有模态函数IMF,并且可以实现IMF 的有效分离、信号的频域划分,进而得到给定信号的有效分解成分,最终获得变分问题的最优解。
1.1 变分问题构造
VMD 将一个信号分解成K 个模态函数,每个模态函数具有中心频率ωk。其可以表述为一个求解K 个带宽总和最小的模态函数的变分问题,约束条件为所有模态函数之和等于原信号
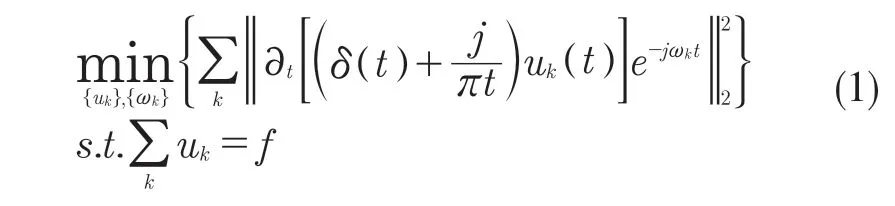
式中:{ωk}={ω1,ω2,…,ωk}代表每个模态的中心频率。
具体步骤如下:
通过对于各个模态函数uk进行希尔伯特变换,得到其解析信号

对每个模态的解析信号混合预估中心频率,并将各模态分量的频率调制到相应的基带频
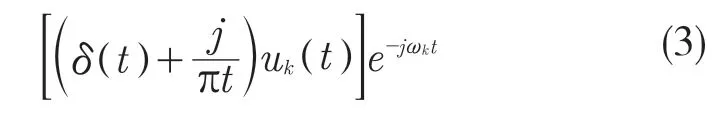
求解上述解调信号梯度的二范数的平方,估计各个模态函数的带宽。
1.2 变分问题求解
为求解上述变分问题,引入二次惩罚因子α和Lagrange 乘子λ(t),将约束变分问题转化为无约束变分问题。其中,二次惩罚因子使得当存在高斯噪声时信号重构的精度得到保证,而拉格朗日乘子使得约束条件严格。增广的Lagrange 表达式如下:
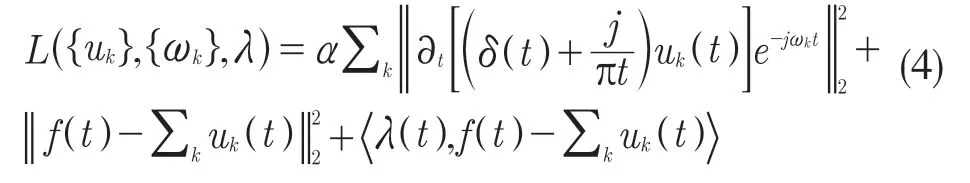
利用交替方向乘子算法(ADMM,Alternate Direction Method of Multipliers)不断更新各个IMF及其中心频率,最终求解式(4)的鞍点,即得到最优解。所有频域中的IMF 及其中心频率可通过式(5)和式(6)求得
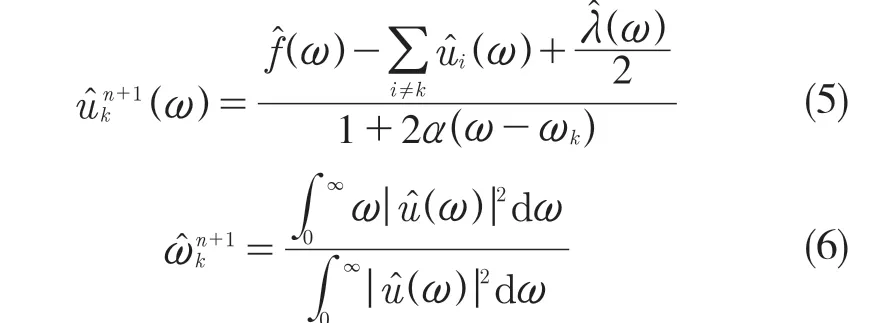
上述即是VMD 的自适应分解过程。VMD 通过在变分问题框架中迭代搜索变分模型最优解来实现信号的分解,其本质是Wiener 滤波,具有很好的噪声鲁棒性,有效规避了端点效应和模态混叠的问题。
2 极限学习机(ELM)
2004 年,Huang[20]等人提出极限学习机 ELM的概念。ELM 是一种新型单隐层前馈神经网络。与传统的前馈神经网络相比,ELM 泛化性高,学习速度快,能够以更加动态和准确的方式计算,在使用时仅需随机给定输入权值和隐含层偏置,并设置隐含层神经元个数,即可求解逆矩阵获取唯一最优解。ELM 网络模型基本结构如图 1 所示。
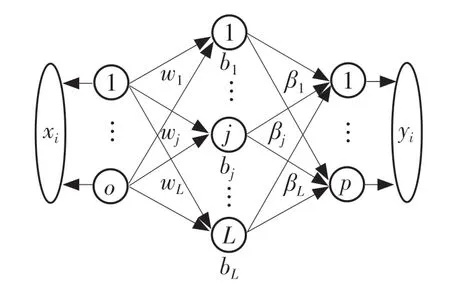
图1 极限学习机模型结构图Fig.1 Structural diagram of extreme learning machine model
给定一组输入输出训练样本集I={xi,yi},其中样本数目为K,维度为o×p。其中,xi是o 维的输入特征向量,yi是p 维的输出向量。用图1所示的ELM 网络训练,则输出表示为

式中:wj——输入层和隐含层神经元间的连接权值;bj(j=1,2,…,L)——隐含层偏置;g(·)——隐含层神经元激活函数;βj——输出层和隐含层节点间的连接权值。简化式(7)为

式中:β——L×p 维输出权值矩阵;H——隐含层输出矩阵;Y——输出矩阵,具体为
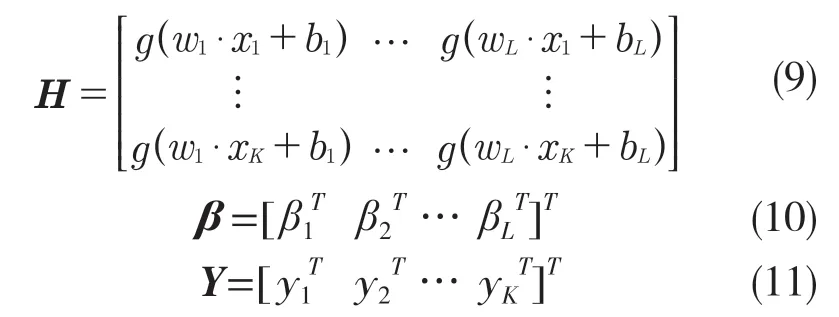
式中:L——隐含层节点数;K——训练样本数。根据Moore-Penrose 广义逆矩阵的定义,可求解出输出权值矩阵β的广义逆矩阵,求解式为
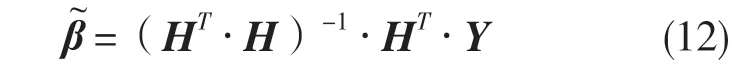
最后,训练并建立ELM 预测模型。根据式(12),ELM 的训练过程是一个线性回归过程,完成输出权值矩阵β的求解后,ELM 模型的训练过程结束。
3 基于VMD-ELM 的锂电池剩余寿命预测
本文提出一种基于VMD 和ELM 的锂离子电池剩余寿命预测方法。首先,利用VMD 分解锂电池容量信号得到一系列IMF;接着基于每个IMF,分别训练ELM 模型,获得各分量预测值;最后,将每个ELM 模型的预测结果加和求得锂离子电池的剩余寿命。其流程如图2 所示,具体包括如下步骤:
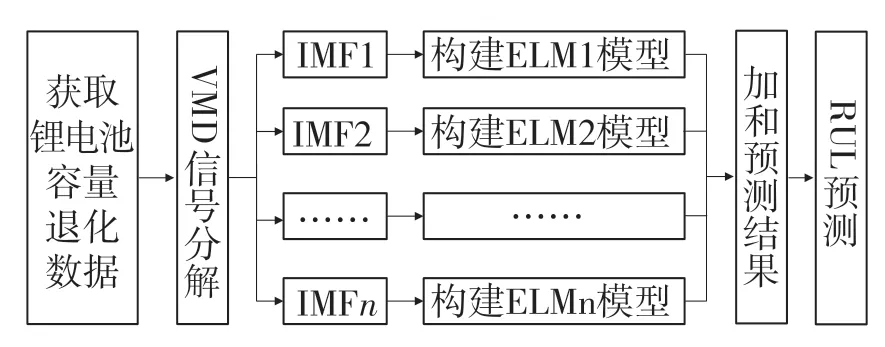
图2 基于VMD-ELM 的锂电池剩余寿命预测流程图Fig.2 VMD-ELM-based lithium battery remaining life prediction flowchart
步骤1:获取锂离子电池放电容量退化数据。
步骤2:以T 周期作为预测起始点,基于1-T周期的数据进行模型训练,以T 周期之后的数据验证预测模型。
步骤3:采用VMD 对原始容量数据进行分解,得到各模态分量IMF1,…,IMFn。
步骤4:分别基于各IMF 构建多个ELM 预测模型ELM1,…,ELMn。
步骤5:将各分量的预测结果相加得到最终剩余寿命预测结果。
4 实验验证
本文采用NASA 提供的锂离子电池数据集1作为实例进行验证[21]。实验锂离子电池额定容量为2 A·h。实验中,采用标准充电方式对电池进行满充,然后采用稳定的2 A 放电电流对电池进行恒流放电,每个实验电池均以放电至2.7 V 的容量作为每个循环周期的放电容量,将额定容量70%作为电池失效的容量阈值。本文以B5,B6电池为例,对所提方法进行验证。B5,B6 电池容量退化情况如图3 所示。由图3 可以看出,随着循环次数的增加,电池容量呈波动下降趋势。
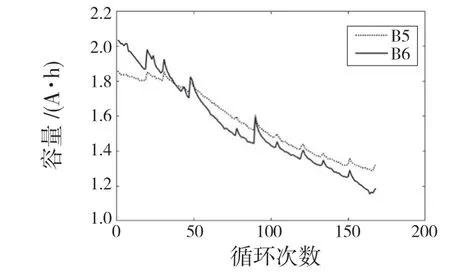
图3 锂离子电池容量退化曲线Fig.3 Li-ion battery capacity degradation curve
设定VMD 分解子序列数k=4,得到相应模态分量如图4 所示。以1~100 循环周期的容量作为训练数据,分解得到的各模态分量用ELM 模型进行预测。为说明基于VMD-ELM 模型的预测性能,在相同条件下采用EMD-ELM,ELM 两种预测模型进行对比,预测结果如表1 所示。由表1 可知,B5 和B6 电池的VMD-ELM 的绝对误差最小,证明使用VMD-ELM 的预测模型精度更高。
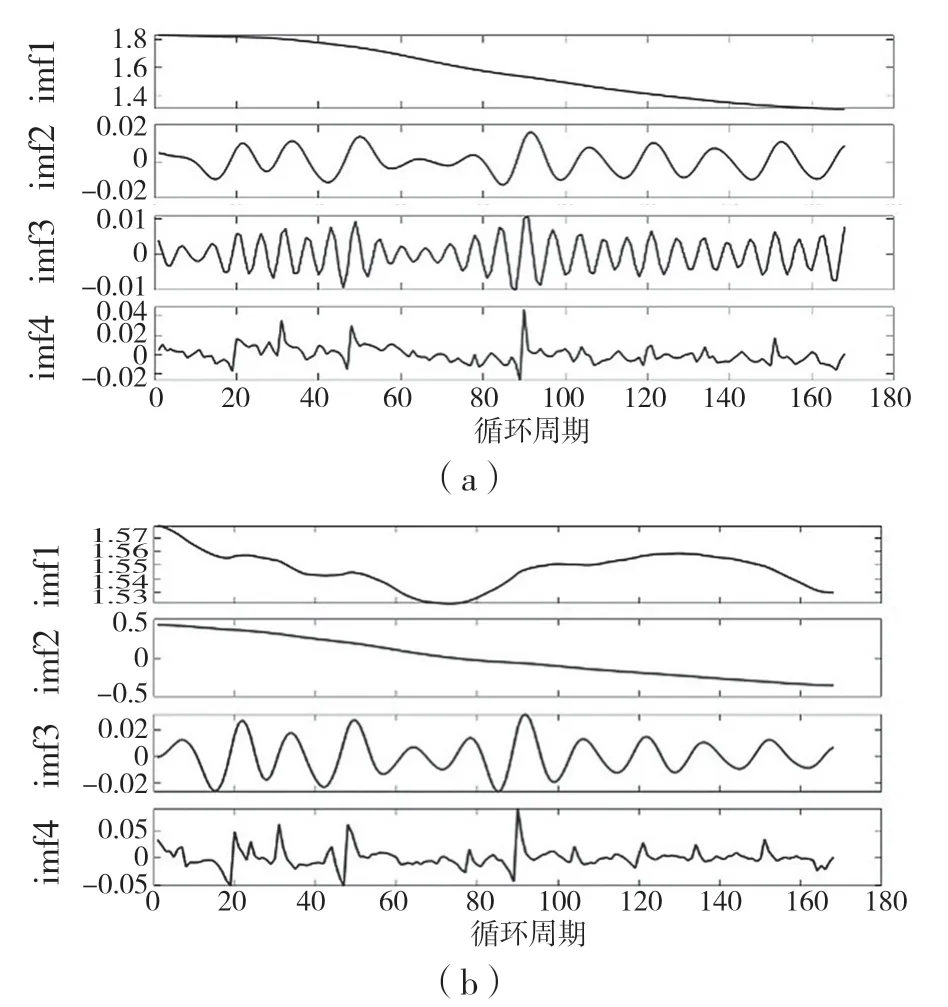
图4 B5、B6 锂电池VMD 分解结果Fig.4 VMD decomposition results of B5 and B6 lithium batteries
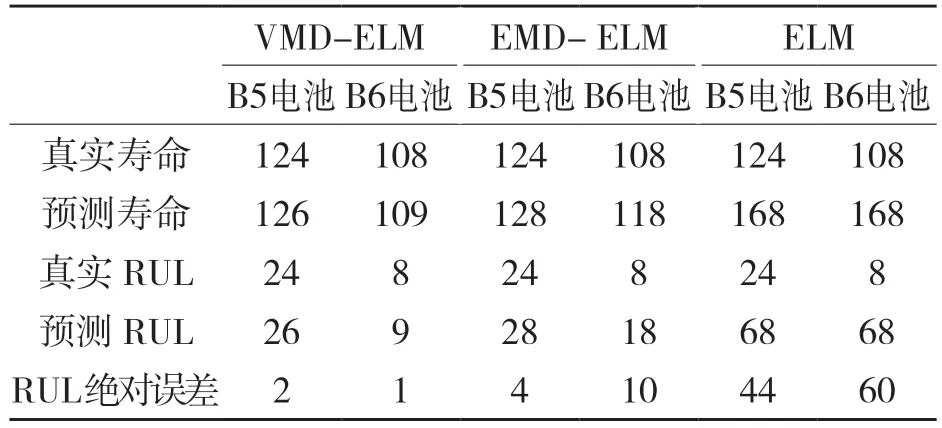
表1 不同方法预测结果Tab.1 Predicted results of different methods
以上为单次预测。为保证结果的准确性,需进行多次预测,选择不同的区间样本按照以上流程预测。预测结果误差分析如表2。本文采用均方误差MSE,平均绝对百分比误差MAPE,平均绝对误差MAE来评估剩余寿命预测结果的精度。
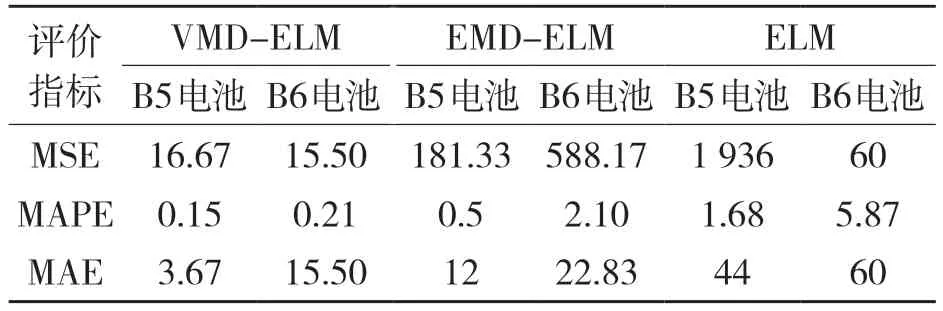
表2 不同方法预测性能对比Tab.2 Comparison of predictive performance of different methods
由表2 可以看出,这三种不同的预测模型中VMD-ELM 模型的预测误差最小,其次是EMDELM 模型,单一ELM 模型预测误差最大。说明基于VMD-ELM 的预测模型进行锂离子电池剩余寿命预测,结果准确度更高,且稳定性较好。
5 结论
针对锂离子电池剩余寿命精确预测的问题,提出基于VMD-ELM 的剩余寿命预测模型。
(1)利用变分模态分解使具有非线性、不稳定的锂电池容量数据分解为多个模态分量,从而使数据更平稳。(2)对于每个IMF 分别采用ELM 模型进行训练,最后叠加预测结果,以提高剩余寿命预测精度。(3)通过NASA 电池实例分析表明,VMD-ELM 预测方法预测结果准确度更高,且稳定性较好。
