锂离子电池电化学-热-力耦合数值模拟及分析

马德正，李培超，岳飞龙，张贝贝，邓辉良

（201620 上海市 上海工程技术大学 机械与汽车工程学院）

0 引言

由于锂离子电池具有较高能量密度和较低自放电率等的优点，因此被广泛应用在各个行业领域。对于锂离子电池的研究也多采用数值模拟的方法。目前，锂离子电池模型大多是基于Doyle[1-2]等建立的拟二维电极模型，模型包含电极动力学、质量守恒和电荷守恒。Prussin[3]等首次将扩散诱导应力与热应力对比；Wu[4]等在粒子和电极尺度上建立了电极电化学和力学的完全耦合半电池模型；Kim[5]等建立了一个三维可重构LiFePO4电极的电化学-力耦合模型，研究了内部扩散诱导应力和电化学降解；Wu[6]等的研究表明，多尺度模型与三维粒子网络模型相比具有很好的一致性。

上述模型均未考虑温度场对电化学和力学的影响。Pals 和Newman[7-8]通过在Doyle 模型的基础上引入能量守恒方程，建立了一个电池运行过程中温度与电化学关系的电化学-热耦合模拟模型；Song 和Evans[9]在电池传热和热管理的数学模型中引入了温度相关参数，以确保模型更加全面；Sato[10]等将电池产热分为3 类：反应热、欧姆热和极化热，并定量评估了各因素对温度场的贡献。但这些电化学-热耦合模型忽略了应力对电化学反应的影响。

实际电池充放电过程受复杂的多物理场影响。Xiao[11]等和Wu[12]等提出了一种多尺度电化学-热-力耦合模型，并对隔膜应力进行了分析。结果表明隔板的应力随循环次数而变化；Duan[13]等建立的二维螺旋电化学-热力耦合模型考虑了应力对扩散的影响，但没有考虑应力场对过电位的影响。

本文的主要目的是建立一个更为全面的电化学-热-力耦合模型，模型考虑应力对电池过电位和锂在电极活性粒子中扩散系数的影响，以及模型部分物性参数对温度场和锂离子浓度的依赖性。该模型对比并分析了电化学-热-力耦合模型与电化学-力耦合模型间的结果差异，以及电池在不同外载下电池电压及容量的变化情况。

1 模型建立

图1 为基于Wu[6]等工作建立的锂离子电池模拟三维多尺度模型原理图。图1（a）为锂离子电池电极水平模型图，模型从左至右分别为正极集流器、正极活性材料、隔膜和锂金属。图中Lp和Ls分别为电极和隔膜厚度，W 为电极宽度，为为粒子间的接触应力，∑xx、∑yy和 ∑xy分别为电极尺度上的主应力和剪切应力。粒子内部总的静水应力σh为浓度导致的粒子内部静水应力与粒子间接触导致的静水应力之和；图1（b）为粒子水平模型图，电极上每点都可以看作由活性材料粒子和孔隙组成的代表体积元（REV）；图1（c）为电化学-热-力多物理场耦合原理图。在Wu[6]等工作的基础上本文引入了温度场并且考虑了模型部分参数随温度的动态变化。

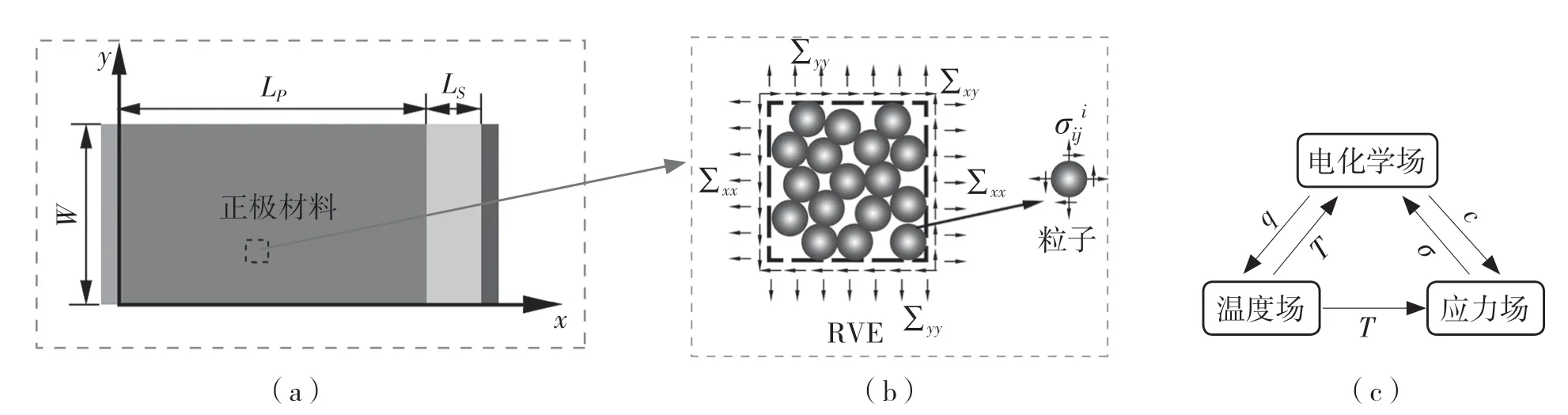
图1 锂离子电池模拟三维多尺度模型原理图Fig.1 Schematic diagram of a three-dimensional multi-scale model of lithium-ion battery simulation

1.1 控制方程

1.1.1 电极动力学

电极活性材料与电解液接触面局部电流密度遵循Bulter-Volmer 方程

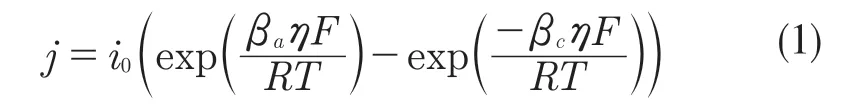
式中：η——过电位；R——气体常数；F——法拉第常数；T——温度；βa，βc——阳极和阴极电荷传递系数；i0交换电流密度计算如式（2）：

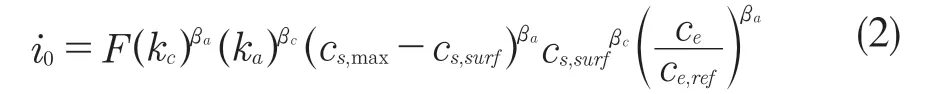
式中：ka，kc——阳极和阴极反应速率常数；cs,max——电极材料最大锂浓度；cs,surf——粒子表面锂浓度；ce——电解液锂离子浓度；ce,ref=1 mol/m3——电解液参考浓度。

1.1.2 电荷守恒

（1）固体相。电子电荷守恒遵循欧姆定律：

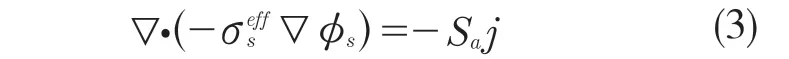
（2）液体相。电解液中离子电荷守恒方程公式如下：

1.1.3 质量守恒

（1）固体相。锂在电极活性材料粒子内的扩散遵循菲克第二定律：

式中：J——电极粒子表面锂通量。

（2）液体相。锂离子在电解液中传递遵循质量守恒：

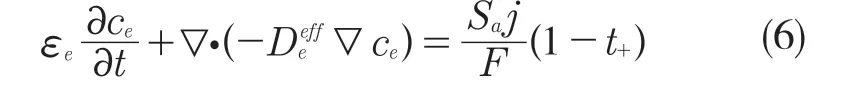
式中：——锂离子在电解液中有效扩散系数。

1.1.4 能量守恒

能量守恒方程：

式中：ρ——密度；Cp——比热容；KT——热导率；Qrea，Qact，Qohm——电化学反应热、活性热和欧姆热。

1.1.5 力守恒

（1）粒子水平。推导粒子内部由温度和浓度所导致的径向应力（r）和切向应力（r）公式如下：

（2）电极水平。电极材料内部总应变ε

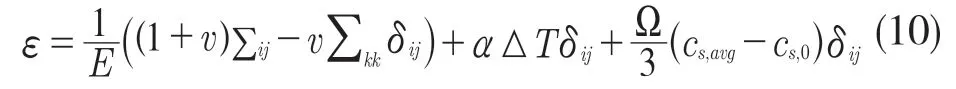
式中：∑ij——应力张量；δij——狄拉克函数；α——热膨胀系数；ΔT——温度变化量；cs,avg——平均摩尔浓度；cs,0——锂的初始浓度；Ep，vp，Ω——粒子活性粒子的杨氏模量、泊松比、粒子摩尔体积。

应力平衡方程为（不考虑体力）：

基于体积平均理论，粒子间接触导致的静水应力（r）为[4]

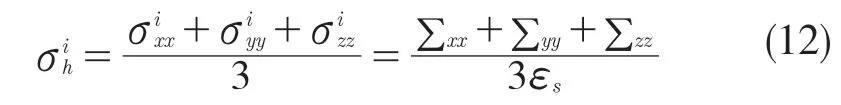
1.2 边界条件

模型电化学场、温度场和应力场上下边界均设置为对称边界条件，模型左右边界条件如下：

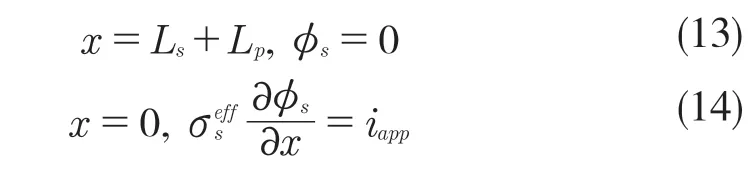
2 模型参数和验证

本文通过参数之间的相互影响来实现电化学-热-力多物理场之间的耦合，原理如图1（c）所示。模型动态参数如下：

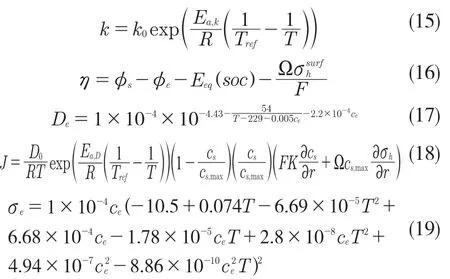
式（16）表示过电位受应力的影响，其中为正极材料开路电压（如图2 所示）。式（18）表示电极粒子内部锂浓度扩散通量受温度和应力影响。热力学因子k 的取值如图2 所示。本文模拟所用参数如表1 所示[6]。

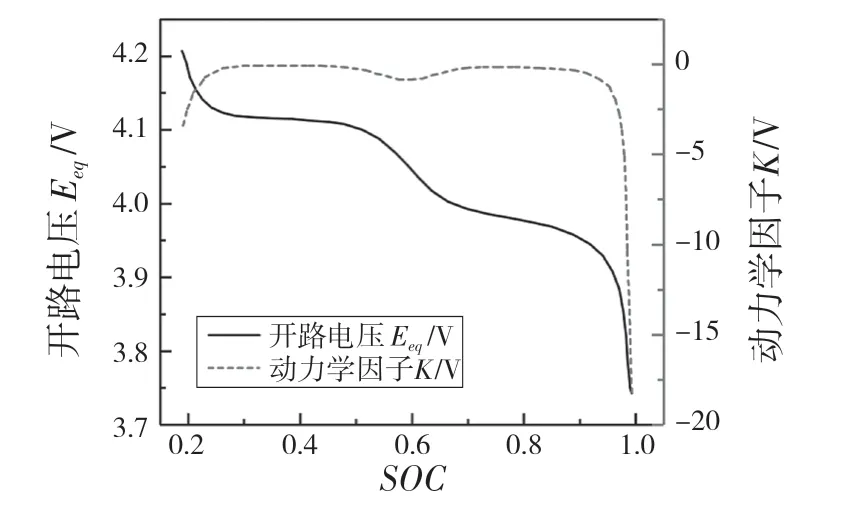
图2 电极开路电压Eeq 和动力学因子K 随SOC 的变化[6]Fig.2 Changes of electrode open circuit voltage Eeq and kinetic factor K with SOC [6]

表1 模拟所用参数Tab.1 Simulation parameters

图3 为电池电压随时间的变化，矩形点图为文献[6]结果，实线为本文多物理场模型退化后计算结果，对比发现本文结果与实验结果一致，验证了本文模型的可靠性。图中点划线为本文电化学-热-力耦合模型计算结果。对比发现，当引入温度对电化学场和应力场的影响后会导致电池的容量和电压的升高，这是由于电化学反应导致模型温度升高，进而促进了电池的电化学反应速率所致。

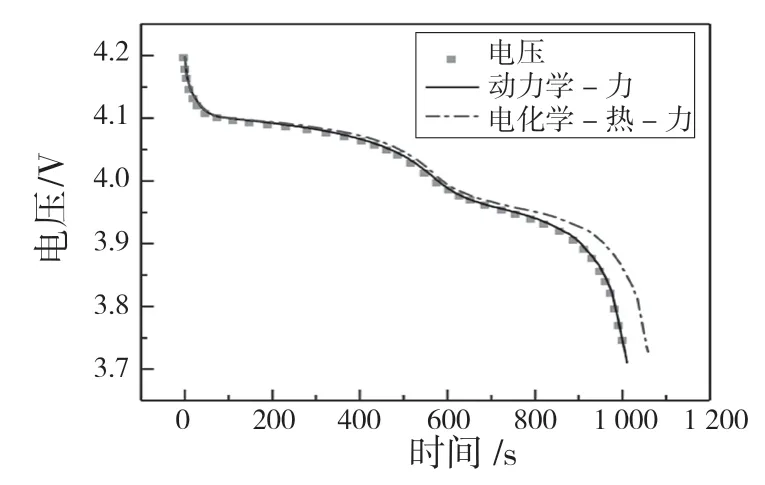
图3 电池电压随时间的变化Fig.3 Battery voltage vs.time

3 结果和讨论

3.1 温度和粒子浓度

图4 为模型温度随时间的变化图。图中点划线表示电化学-热-力耦合下温度随时间的变化，实线为电化学-力耦合下的温度变化。结果发现，考虑温度对其它物理场的影响因素后导致模型温度会变低，两者温度的差异表明电化学-热-力耦合和电化学-力耦合模型差异显著。

图4 温度随时间的变化Fig.4 Temperature vs.time

图5（a）和 图5（b）分别表示在x=0 和x=Lp位置处粒子中心r=0 和表面r=R0浓度随时间的变化趋势。对比图5（a）和（b）发现，正极靠近隔膜位置（即x=Lp）处粒子表面浓度将快速增加并在t=100 s 后增速变缓慢，t=400 s 后粒子中心浓度增速变大；电极远离隔膜位置处（即x=0）粒子表面浓度增速相对更均匀和缓慢，粒子中心浓度会在t=540 s 后快速升高。同时，从图中可看出，当模型中引入温度场对电化学场和应力场的影响后结果变化显著，且粒子内部浓度会变得均匀，这是由于锂在粒子内部的扩散通量受温度和静水应力的共同影响导致。

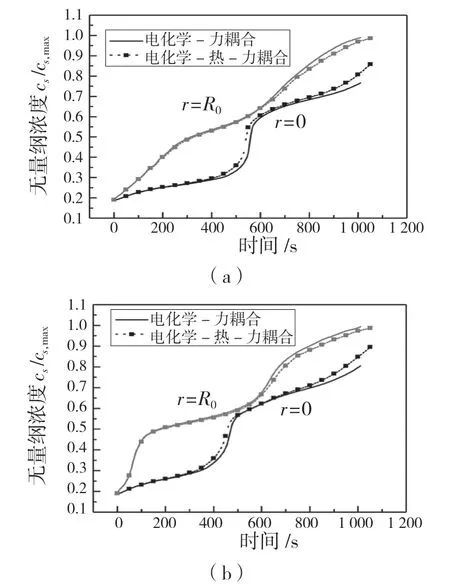
图5 粒子中心和表面浓度随时间的变化Fig.5 Changes in particle center and surface concentration over time

3.2 外载对电极影响

在不同放电速率（0.1×iapp，0.25×iapp和iapp）条件下对本文模型右端施加不同外载（0 psi和1 000 psi）观察外载对正极材料的影响。图6表示模型在不同放电速率和外载时电池电压随容量的变化趋势。由图6 可知，放电速率增加会导致电压放电平台和电池容量的降低。对比图中实线和点线发现，模型右端施加外载会导致电池容量和电压平台的降低，这是因为电极内部应力的变化会导致电极过电位的改变进而影响电池放电性能，如式（16）所示。同时，对比图中不同放电速率下的曲线发现，外载对低放电速率下的电池性能影响比对高放电速率下性能的影响更大，这是由于高放电速率下粒子内部浓度极化更显著，导致电极粒子内部应力水平较大，从而导致外载荷对高速率放电状态下电极性能的影响较小。

3.3 隔膜变形的影响

由图6 发现，外载为1 000 psi 时对放电速率为iapp下的电池性能影响很小。考虑到电池实际受压过程中隔膜同样受到挤压，故此处在本文应力模型中引入隔膜孔隙度变量ε=（ε0+εv）/（1+εv）探究隔膜组件在外载下的变形对电池性能的影响。此处取隔膜初始孔隙度ε0=0.39，εv为隔膜体积应变，隔膜杨氏模量Esep和泊松比vsep取值如表1 所示。考虑隔膜在外载作用下的变形后电池电压随容量的变化图，如图7 所示。

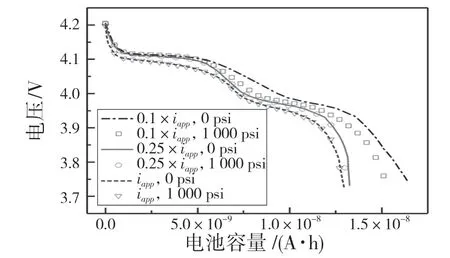
图6 不同放电速率和外载对电池电压随容量变化的影响Fig.6 The influence of different discharge rate and external load on the change of battery voltage with capacity

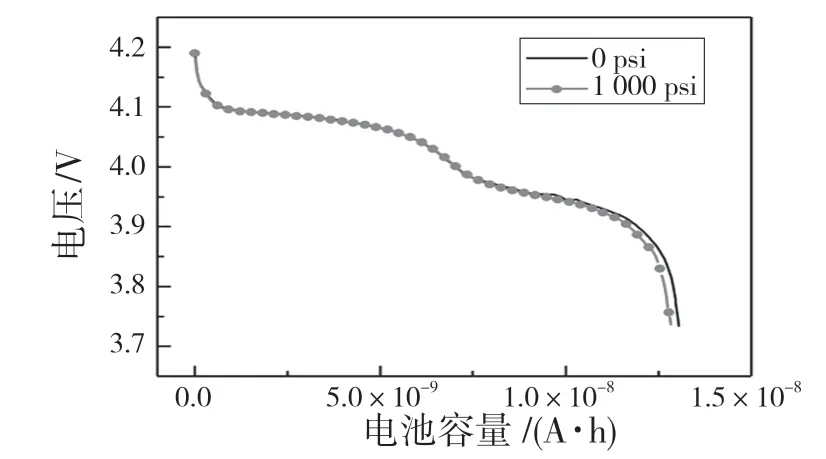
图7 隔膜在外载作用下的变形对电池电压随容量变化的影响Fig.7 The influence of separator deformation under external load on the change of battery voltage with capacity

图7 中点划线为在电池右端施加1 000 psi 外载，实线表示载荷为0。对比发现，考虑隔膜孔隙度变化后，电池容量和放电电压平台均会有所降低，这是由于应力在影响电极的过电位和扩散系数同时也会压缩隔膜导致隔膜孔隙度减小，进而影响电池放电性能，今后模拟外载对电池影响过程中必须考虑隔膜压缩所导致的隔膜孔隙度的动态变化。

4 结论

建立了一个锂离子电池电化学-热-力全耦合数学模型，使用COMSOL Multiphysics 求解。通过与前人结果对比验证了本文模型的正确性。利用该多物理场耦合模型探究了温度场、外载以及隔膜变形对电池电压及容量的影响。结论如下：

（1）模型引入温度场对电化学场及应力场的影响后会导致电池的容量和电压有所提升，同时模型产热减小从而温度变低。引入温度场导致粒子内部锂的扩散通量增加，因此粒子内部浓度相比电化学-力耦合更均匀。

（2）放电速率和电池外载的增加会导致电池电压和容量的降低，且同等外载荷对低放电速率下电池性能的影响更显著。

（3）对电池施加外载会导致隔膜孔隙度减小进而造成电池放电电压和容量的降低。

在今后对电池压缩性能的模拟分析中必须要考虑隔膜孔隙度变化对电池性能的影响。