电动汽车PMSM 电磁场分析及铁损计算

黄捷思，曹民，曹建荣

（1.200093 上海市 上海理工大学 光电信息与计算机工程学院；2.201804 上海市 上海汽车集团股份有限公司 前瞻技术研究部）

0 引言

永磁同步电机作为电动汽车的核心部件，拥有效率高、体积小等优点，而永磁同步电机属于紧凑型电机，运行过程中因散热不易而影响电机性能，如何减轻损耗减小散热成为电机设计一大难点。电机损耗中铁芯损耗占比较大。最经典的电机铁芯损耗模型是由Bertotti 提出的铁耗分离模型[1-3]，该模型由磁滞、涡流和附加损耗组成，模型中的未知系数即使在同一材料的情况下也不是一成不变的[4]。该模型适合磁密波形接近正弦的磁场，故适用范围较小；而实际电机磁场是非正弦的，处于交变磁场和旋转磁场的共同作用下[5]。文献[6]建立了双闭环电路驱动下的二维电磁场-电路耦合计算模型计算并通过时步有限元分析了SRM的磁场和定子铁心损耗，验证了时步有限元的可行性；文献[7]利用时步有限元法分析了一台高速永磁同步电机磁场特性及不同负载对定子铁心各区域的损耗的影响。

本文在Bertotti 模型的基础上，以一台4 对极、72 槽的永磁同步电机为例，建立二维有限元电机模型，运用最小二乘法求出铁损系数，使用铁损系数及磁通密度构成多项式进行回归分析，考虑电机中谐波和旋转磁场，将磁密波形分解为径向与切向，根据谐波分析原理，对其进行快速傅里叶分解，并将计算结果与有限元仿真及Bertotti铁心损耗模型进行对比。结果表明，计算电机铁耗时需要考虑电机磁场的谐波损耗。

1 电机二维时步有限元分析

本文分析的电机为4 对极、72 槽。利用ANSYS Maxwell 建立二维有限元模型，并在定子铁心上选取5 个点位，如图1 所示。永磁同步电机工作时，由于饱和严重，采取平均磁通计算铁芯损耗会带来较大误差，而电机运行时铁芯内除了交变磁场还存在旋转磁场，为了能更好地计算损耗，需要确定铁芯内部的磁密变化。

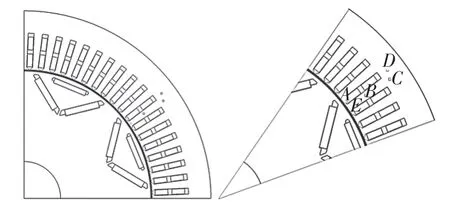
图1 电机1/4 二维有限元模型及选点Fig.1 Motor 1/4 two-dimensional finite element model and point selection

采取时步有限元法对电机定子进行电磁场分析，在定子上选取齿尖A、B、C、D、E 五个点，在1 000 r/min 下计算电机运行一个电周期360°各点的磁密变化。根据谐波分析原理，电机中任意一点磁密波形都可以通过快速傅里叶分解得到基波和多次谐波，铁心的损耗就等于磁密基波及各次谐波产生的总和。考虑电机旋转磁场的影响，将磁密波形分解为径向Br与切向Bt。限于篇幅只给出A、C 点的磁密随电角度变化，如图2 所示。

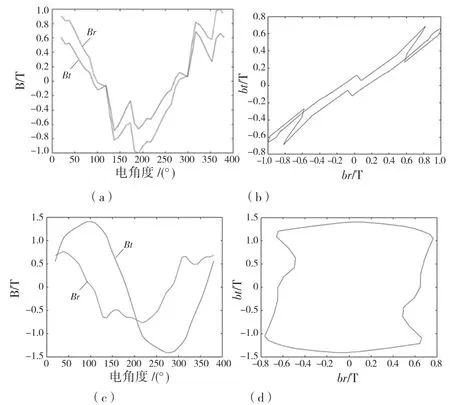
图2 时步有限元分析结果Fig.2 Results of step-by-step finite element analysis

从径向切向磁场图可以看出，除了齿顶（A、E）是受交变磁场影响外，其他点位（B、C、D）均同时受交变磁场及旋转磁场的影响。

图3 给出A 点与C 点的各谐波幅值。可看出，齿根（C）磁密切向幅值大于径向幅值，而齿顶（A）则相反。齿顶高次谐波幅值较大。

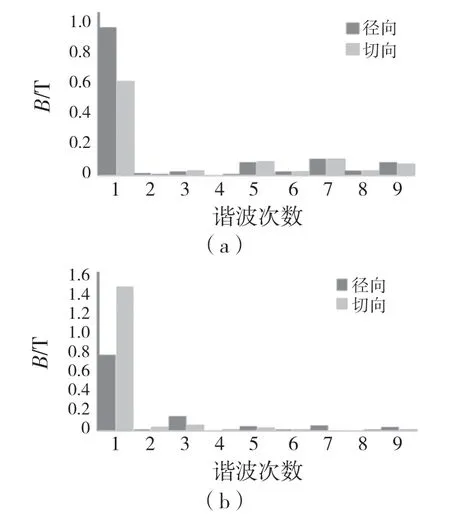
图3 点A 与点C 磁密波形径向切向谐波次数Fig.3 The number of radial tangential harmonics of point A and point C magnetic density waves

2 电机铁损计算

2.1 铁心损耗计算模型

Bertotti 提出的铁损分离模型如下：

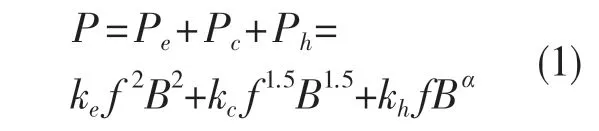
式中：Ph——磁滞损耗，Ph=khfBα；Pe——涡流损耗，Pe=kef2B2；Pc——附加损耗，Pc=kcf1.5B1.5；kh，ke，kc——磁滞、涡流和附加系数；f——频率；B——磁密幅值；α——磁滞功率系数，为方便计算，假设α=2[8]。

附加损耗在整个定子铁芯损耗里占比较小[9]，令ke=0，假设后的公式：

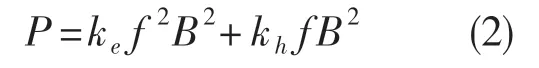
2.2 铁损模型系数确定

将式（2）变形：

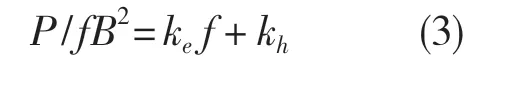
令Ke=b，kh=α，则P/fB2=a+bf，通过最小二乘法，可以计算得出系数ke，kh。计算结果见表1。

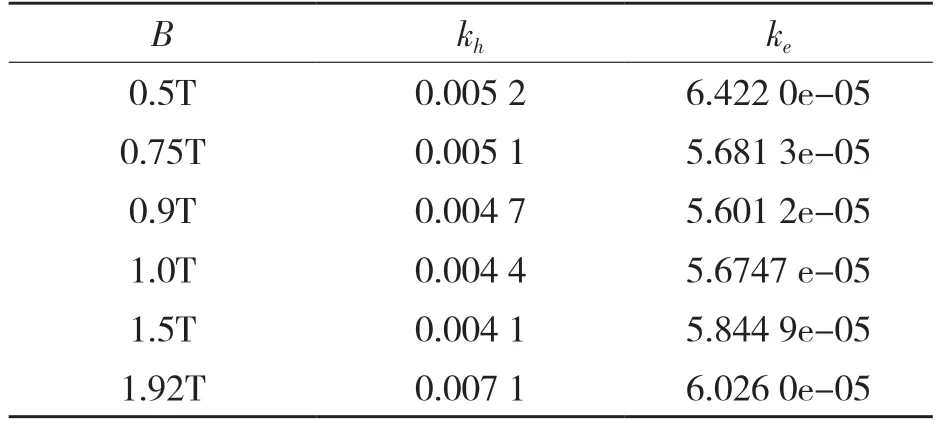
表1 各磁密下的kh、ke 系数Tab.1 kh and ke coefficients under each magnetic density

同时将计算得到的ke、kh，使用以下5 阶多项式进行拟合

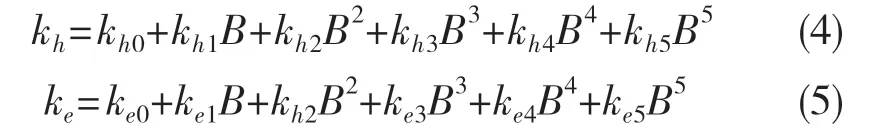
考虑旋转磁场以及交变磁场，根据谐波分析原理，将磁密径向及切向的基波及各奇次谐波幅值代入铁损模型式（2）得到式（6）：

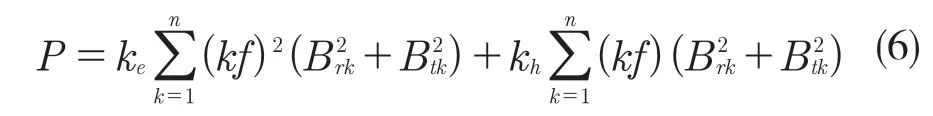
式中：k——谐波次数；Brk，Btk——铁心磁密径向及切向磁密波形次谐波分量幅值。

由式（4）、式（5）拟合得到的曲线如图4 所示。

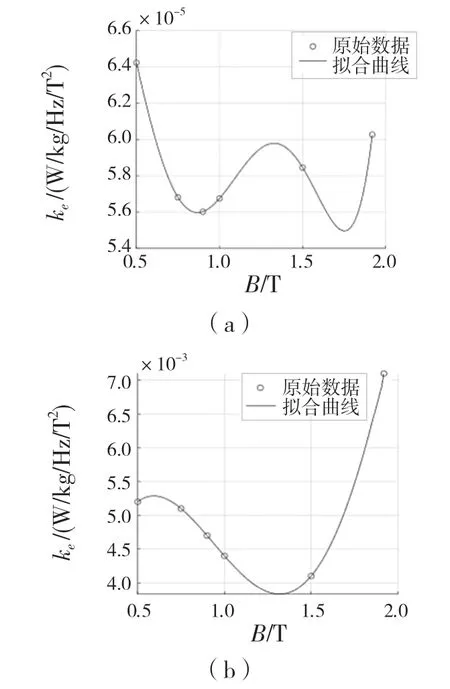
图4 多项式拟合Fig.4 Polynomial fitting

通过式（6）可以计算出该点所在部位单位质量的铁芯损耗，总体的铁芯损耗等于每个部位计算出来的各个连续小单元的单位质量的损耗之和，如式（7）所示。

式中：L——电机铁心轴向长度；ρ——电机铁芯质量密度；ΔSj——电机第j 个单元面积；n——电机总单元数；pj——电机第j 个单元的单位质量铁芯损耗。

3 计算结果分析

将有限元分析得到的磁密幅值代入式（4）、式（5）求得各点的铁损系数，如表2 所示。

表2 1 000 r/min 下各点电机铁损系数Tab.2 Iron loss coefficients of motor at each point at 1 000 r/min

根据谐波分析原理对磁密波形进行傅里叶分解后得到各点基波及其各次谐波幅值，将其代入式（6），再根据表2 中的铁损系数分别求得电机铁芯各点单位质量的磁滞、涡流损耗以及总损耗，如表3 所示。

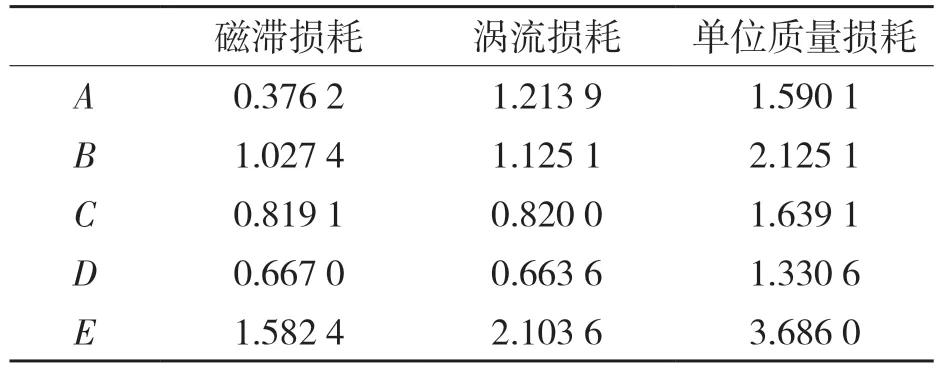
表3 1 000 r/min 下各点单位质量的损耗Tab.3 Loss per unit mass at each point at 1 000 r/min

由表2、表3 可知，齿身、齿顶（B、E）的单位质量铁损比其他位置高，各点磁滞损耗均比涡流损耗小，涡流损耗占单位质量损耗的56.2%。根据式（7）计算出考虑谐波和旋转磁场的电机总铁芯损耗，并与不考虑旋转磁场和交变磁场Bertotti 模型的有限元仿真结果进行对比，结果如图5 所示。

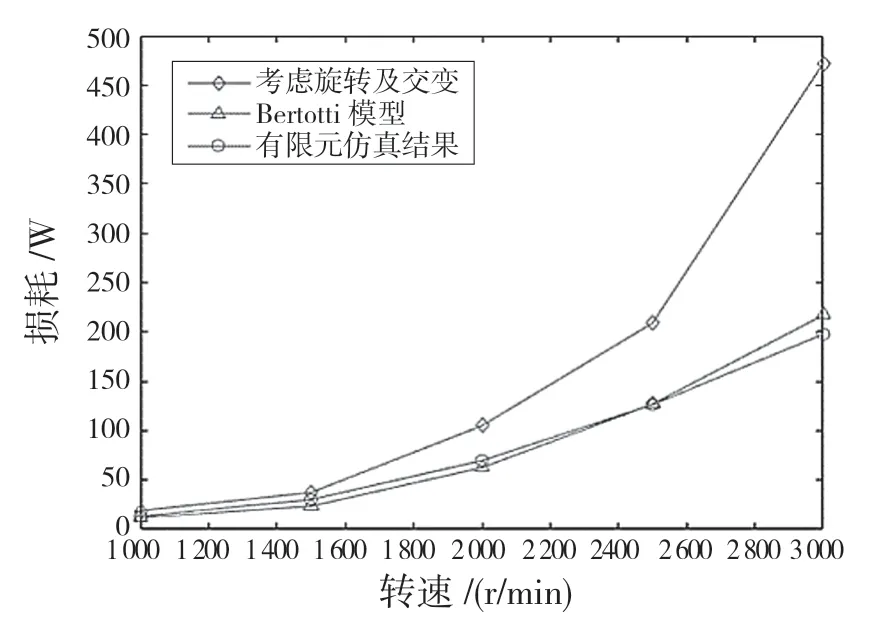
图5 结果对比Fig.5 Comparison of results

由图5 可知，当电机转速在1 500 r/min 以下时，电机铁损基本符合有限元仿真结果与Bertotti铁损模型结果，而随着电机转速升高，铁芯内部磁场谐波含量增加，谐波损耗变高，这时需要考虑谐波对铁芯损耗的影响。

4 结论

本文分析了一台4 对极、72 槽永磁同步电机各转速下的铁芯损耗，提出一种铁损系数随磁通密度变化的铁损模型，并根据谐波原理，通过对磁密波形进行分解，取径向切向的各次谐波幅值代入本文提出的铁损模型中，将结果与有限元对比。低速下的结果与有限元基本一致，但随着转速升高，电机谐波损耗占比变高，这部分损耗不可忽略。本文提出的铁损模型可为电机损耗计算提供精准解决方案。