基于正交实验的音圈电机参数权重分析

黄运泽，王利强，李佳武，白 雪

（天津职业技术师范大学 电子工程学院，天津300222）

出力大小是反映音圈电机性能好坏的一个重要因素，影响出力大小的因素有线圈电流、线圈线径、气隙以及线圈匝数等。根据外形结构不同，音圈电机分为平板型、圆筒型、弧型；根据动子结构不同，音圈电机分为动磁式和动圈式。成本低且高精度的直线电机是未来直线电机的发展方向，不难看出，在高精密使用场景方面，动磁式音圈电机具有明显的优势[1-2]。本文主要研究了圆筒型动磁式音圈电机的出力情况，采用三因素四水平正交分析实验分析线圈电流、线圈匝数、气隙对出力的影响，借助ANSYS Electronics Desktop 中的Maxwell 软件进行有限元数值模拟，并对所建立的模型进行验证，得出影响出力大小的主次因素，这对于音圈电机的实际应用有重要的参考指导意义。

1 有限元分析模型的建立

本文所采用的模型为动圈式音圈电机的基础模型，其简易结构如图1 所示，主要由永磁体、线圈和线圈支架组成，线圈以及支架作为动子，永磁体作为定子[3]。当线圈内通入电流后，在永磁体所产生的磁场中受到电磁力的作用，根据左手定则，线圈绕组会受到轴向推力，推力随着通入电流大小所改变，当电流方向改变时，线圈沿轴向做往复运动[4]。

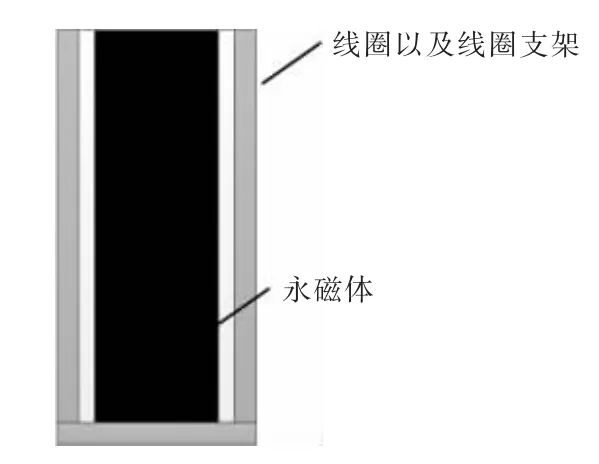
图1 简易结构图Fig.1 Simple structure diagram

线圈的建模一般分为2 种不同的方法，如图2所示，一种建模方式是solid 建模，其特征是按照实物建立具体线圈模型。另一种是stranded 建模，其特征是建立矩形区域，设置其内部参数，以安匝数的形式通入电流模拟线圈。为简化仿真过程，所阅读文献中大都采用stranded 建模。但是本文正交实验的设置过程中，需要考虑到线圈绕制匝数和线圈线径的因素，故采用了solid 建模方法[5]。本文所用的模型如图3 所示，由于电机结构关于中心轴对称，所以建立模型时可以建立电机的半剖面来代替整个电机。其中永磁体所属材料为N35 钕铁硼，线圈所属材料为铜，永磁体材料参数如表1 所示，线圈材料参数如表2 所示。

图2 线圈建模类型Fig.2 Coil modeling types

图3 音圈电机2D 仿真模型Fig.3 Voice coil motor 2D simulation model

表1 永磁体材料参数Tab.1 Permanent magnet material parameters

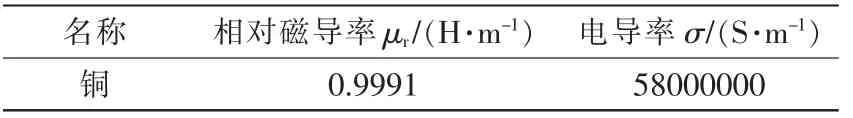
表2 线圈材料参数Tab.2 Coil material parameters

2 有限元分析模型的可靠性验证

仿真分析可得出通电线圈在永磁体所产生的磁场中受到的电磁力大小。将其制作成实际模型，其主要的结构参数： ①定子永磁体为径向充磁的NdFeB35SH 型钕铁硼，直径为32 mm，高为72 mm；②线圈绕组采用标准规格的0.5 mm 漆包线绕制。

测试平台如图4 所示，在保证测力计与线圈同心前提下，使用直流电源对线圈绕组通入对应电流，由左手定则判断线圈受力，调整电路方向，使其沿永磁体轴向运动，触碰到测力计时即为此种情况下线圈受力情况。

图4 测试平台Fig.4 Test platform

根据改变线径以及电流大小的实验对比测量，所测得的数值与仿真结果基本吻合，具有相同数量级的趋势，证明了仿真模型搭建的可靠性。

3 正交实验设计

多因素实验设计中经常遇到信息量与实验规模的矛盾，随着影响因素的增加，所需实验次数也随之增加，而当实验次数增加时，不可避免地会使每个因素隐含着重复实验的信息。而基于数理统计和正交原理可列出该实验的正交表，根据正交性求出最优的、高效率的实验设计。

正交实验设计就是在做试验前用现成的正交表，合理选择实验条件，并对试验结果进行分析，这样既可以减少试验次数，又可以确定各要素对试验结果的影响，从而根据其影响的大小确定主次关系。

正交表是一种特别的表格，是正交试验的基本工具，用正交表LN（qS）做实验时，L 代表正交表的代号，N 代表正交表的行数，即为需要做的实验次数，q代表各因素的水平数，S 代表正交表的列数，即为最多能安排的因素个数，包括交互作用、误差等。

正交试验设计的基本步骤可分为以下5 步：①确定目标、选定因素（包括交互作用）、确定水平；②选用合适的正交表； ③按选定的正交表设计表头，确定试验方案；④组织实施试验；⑤实验结果分析。

4 基于正交试验的音圈电机设计参数的敏感性分析

4.1 正交试验的敏感性分析流程

音圈电机是一种直线电机，广泛应用于各个工业领域，在高频响运动领域尤为突出，而其出力大小是其关键的评价标准。然而，从电磁理论上不容易定量分析出音圈电机各因素对其出力的影响，本文笔者采用正交试验分析了音圈电机各个因素对出力的敏感性影响，主要包括试验因素的选择、正交表的建立以及对于正交试验结果的敏感性分析。

4.2 试验因素的选择

电磁力大小理论计算公式为

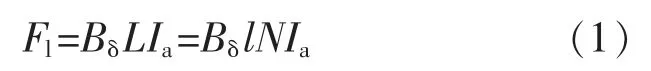
式中：Bδ为磁感强度；l 为每匝线圈的长度；N 为线圈的匝数；Ia为线圈所加的电流的大小。其中Bδ和L 是由电机的尺寸、还有电机的材料来决定，并且称BδL 为电机的力常数，可以得出对电磁力有影响的因素有永磁体所提供的磁场强弱、每匝线圈的长度、线圈的匝数以及线圈的电流。

经综合考虑将线圈匝数、线圈电流以及影响磁感强度的实际气隙作为可调因素。此处所指的气隙是线圈到永磁体表面的水平距离，由于试验所用的圆筒型音圈电机绕组线圈一般只能采用并排密绕的方式，这种绕制工艺使得圆筒型音圈电机的出线较为特殊，为了使进线和出线同侧，绕组只能是2层、4 层或6 层等偶数层。根据设计因素工艺所选线圈层数分别为2 层、4 层、6 层、8 层，通过线圈直径计算故而线圈匝数分别为288 匝、576 匝、864 匝、1152 匝；线圈电流也不宜过大，电流过大时，线圈受热而导致线圈绕组受力出现波动，选择0.5 A、1 A、2 A、4 A；气隙所选择为0.5 mm、1 mm、1.5 mm、2 mm。可调因素所设计的水平配置如表3 所示。

表3 可调因素水平参数Tab.3 Adjustable factor level parameters

4.3 正交表的选择

根据影响音圈电机出力的因素个数以及水平，选用三因素四水平正交表，表示为L16（43），如表4所示。

表4 正交表设计Tab.4 Orthogonal table design

4.4 基于正交试验的敏感性分析

正交试验常用的分析方法有极差分析和方差分析，极差越大，范围跨度越大，极差越小，范围跨度越小；方差越大，波动值就越大，对试验因素的影响就越大。一般是通过极差分析的方法来判定试验因素的权重值大小，极差值越大说明该实验因素对实验结果的影响越大，以反应实际参数的敏感程度[6]。根据式（2）可计算出各因素的极差值，式（3）可计算出各因素的均值。

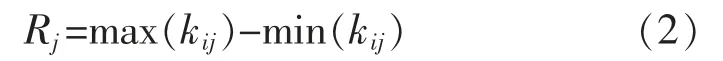
式中：kij代表第j 列i 水平所对应试验结果的平均值；xin代表i 水平的第n 次试验所对应的因素值；m代表单水平所重复的试验次数；Rj代表第j 列所对应因素的极差值，极差值越大，表示该因素的敏感性越大，单位变量对试验结果所产生的影响越大。如表5 所示为出力大小的极差分析结果，由极差大小可知对音圈电机出力的敏感性大小顺序：线圈电流＞线圈匝数＞气隙。

表5 音圈电机出力大小的极差分析结果Tab.5 Results of the extreme difference analysis of the size of the voice coil motor output force

5 多元线性回归分析及验证

5.1 多元线性回归模型

线圈的匝数（N）、绕组中的电流（Ia）、音圈电机气隙（Q）与音圈电机出力（f）之间存在线性特征，欲采用多元一次线性回归方程拟合它们之间的函数关系，对各个参数进行归一化处理[7]，即为式（4）：

式中：xi代表正交表中各水平可调参数；Xi代表各参数归一化处理后的值。

选择多元线性模型作为回归模型，利用minitab19中的拟合回归模型对表3 中16 组正交数据进行分析，所得模型的拟合优度为93.02%，它是衡量方差分析得到的回归方程优劣或合适与否的一个重要参数，是回归平方和占总离差平方和的比率，其数值越接近于1，代表得到的回归方程越好或越适合（模型拟合越好），所得函数表达式见式（5）：

5.2 回归模型的验证

对所得回归模型计算结果进行了仿真验证，图5 所示为音圈电机出力的方针结果与回归曲线计算结果的对比。

图5 音圈电机出力仿真结果与回归曲线计算结果对比Fig.5 Comparison between the simulation results of voice coil motor output and the calculated results of regression curve

由图5 可见，仿真结果与有效的回归计算结果图中，试验值与预测值的误差在回归线的精准度范围之内（S=56.9140），验证了回归函数的准确性和可靠性。

6 结语

引入正交试验的方法分析了关于音圈电机出力的各个因素的影响，分析结果表明，各因素对音圈电机出力的敏感性大小顺序为线圈电流影响最大，线圈匝数次之，气隙影响最小。根据各参数对出力的敏感性，可以为音圈电机的设计提供理论基础，以增加其实用性。

基于正交试验的各个因素对音圈电机出力的影响为各种类型的音圈电机设计提供一个新的理论思路，在工程方面可以按照本文思路对所用音圈电机进行进一步的优化设计，使设计方案更加完善。

通过对正交试验结果的分析建立了电磁力与线圈电流、 匝数以及气隙之间的多元线性回归模型，并得到回归方程并验证其有效性，可作为将音圈电机参数化的关键基础。