角膜变形的三维球对称模型分析
2021-11-25任巧妹高志鹏李永胜
任巧妹,高志鹏,李永胜,陈 静
(太原理工大学 a.生物医学工程学院,b.机械与运载工程学院,太原 030024)
角膜是位于眼球前端的透明软组织,为眼睛提供三分之二的屈光度[1],是视觉系统中非常重要的一部分。角膜生物力学特性是角膜内在的固有属性,主要是角膜对抗外力产生形变的能力。角膜的生物力学特性在角膜形状的维持、屈光手术的设计以及人工角膜的研发等方面均有重要作用。此外,角膜生物力学特性的研究也有助于眼压测量、青光眼管理等。近年来,国内外越来越多的学者开始关注角膜生物力学,并在圆锥角膜、屈光手术、青光眼等领域取得一定的研究进展[2-3]。角膜生物力学近年来越来越受到眼科临床的重视。
目前,研究角膜力学特性的方法很多,典型的体外测试方法有轴向拉伸实验[4-5]、整体膨胀实验[6]以及压痕实验[7]等,实验测试方法不同,获得的角膜力学参数的数值也不尽相同,还有应用于眼科临床的在体测试技术,如眼反应分析仪(ORA)和可视化角膜力学分析仪(Corvis-ST),然而其测量参数较难建立与经典力学之间的关系[8],将其应用于角膜力学特性的研究并未取得突破性的结果。轴向拉伸实验是使用最广泛的测角膜力学性能的方法[9],膨胀实验可以保证角膜组织的完整性,接近真实地模拟角膜在眼内压作用下的变形响应[10]。然而单轴拉伸实验释放了完整角膜在生理眼内压作用下的预应力,破坏了角膜的正常生理结构[11]。本文尝试改进膨胀实验,在保留完整眼球的基础上对角膜行压痕实验,力图在维持角膜自然受力环境的基础上,测试不同眼内压下角膜的力学性能。
有研究表明[12],当眼内压在较低范围内(p<2.67 kPa)不断升高时,角膜表面各区域的曲率保持不变,即角膜形态不变。为了研究角膜的相关疾病,需要对角膜结构进行精确的生物力学建模。然而由于角膜具有各向异性与高度粘弹性,对其力学特性的研究较为困难。本研究通过对完整角膜进行压痕实验,得到角膜的等效弹性模量,并基于球对称理论分析角膜径向、周向的应变响应,发现完整角膜的体积应变呈现均一性,为后续术后角膜力学性能的研究提供理论基础。
1 材料与方法
1.1 角膜试件制备及压痕实验
从屠宰场获取8个死亡1 h内6~8月龄的家猪眼球,雌雄随机。快速摘取眼球,并防止刀具损伤以保证角膜结构的完整性,将摘取下来的眼球放入保鲜袋,存于内置干冰的4 ℃保鲜盒中运输至实验室。在实验室,使用PBS缓冲液清洗眼球,并用眼科剪以及眼科镊将眼球筋膜、结膜、眼外肌及视神经等眼球的附属组织去除(保留约5 mm长的视神经),整个制备过程在2 h内完成。所使用的完整角膜样本,即眼球完好时,角膜样本的相关参数如等效曲率半径Rc、平均厚度t以及连接角膜缘与角膜曲率中心的角度φ如表1所示。
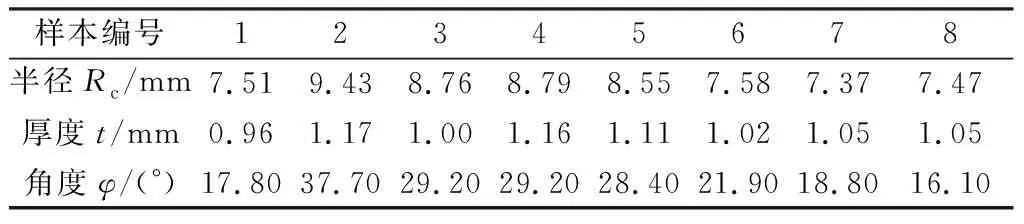
表1 完整角膜样本的相关参数Table 1 Relevant parameters of complete corneal samples
实验时,将眼球置于充满PBS缓冲液的固定装置中,使用注射器调节液压进而控制眼内压。压痕实验前,用回弹式眼压计(FA800vet,FuAn,中国;分辨率:±1.5~2.5 kPa)测量眼内压,压痕装置如图1所示。实验时,将角膜完全暴露在压痕探针的测试区域,用自制直径为1 mm的钢球固定于5 N的力传感器上,使用Instron 5544材料试验机对角膜进行压痕至0.3 mm,其加载速率为1 mm/min,实验过程使用CCD(charge coupled device)相机进行图像采集,以便角膜相关信息的测量。
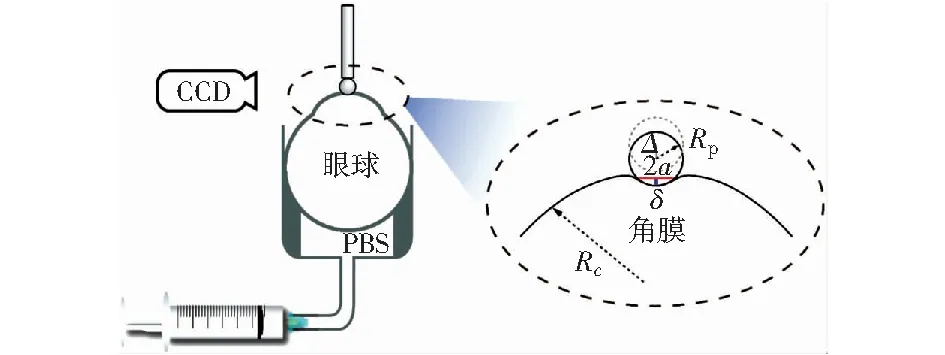
图1 压痕实验装置示意图Fig.1 Schematic diagram of indentation test device
1.2 等效弹性模量计算
角膜的压痕过程可以视为两个球体的接触问题,即一个刚性小球压入一个相对较大且柔软的完整眼球(图1).本文着眼于压痕实验所得力-位移曲线的加载阶段,采用考虑黏附能的Johnson-Kendall-Roberts(JKR)模型[13]计算其等效弹性模量值E(图2),即
式中:R=RcRp/(Rc+Rp) 为等效半径,Rc、Rp分别是角膜与球形探针的半径;ν为泊松比。相关文献报道干角膜的泊松比约为0.05[14],而角膜不同区域的泊松比在0.12~0.40之间[15],不可压缩的有限元模型中通常将泊松比设为0.47[16].γ=W/A为单位接触面积的黏附能,W为黏附能,A为球形探针与角膜的接触面积;δ为压痕深度,a为接触半径,F为压痕力。
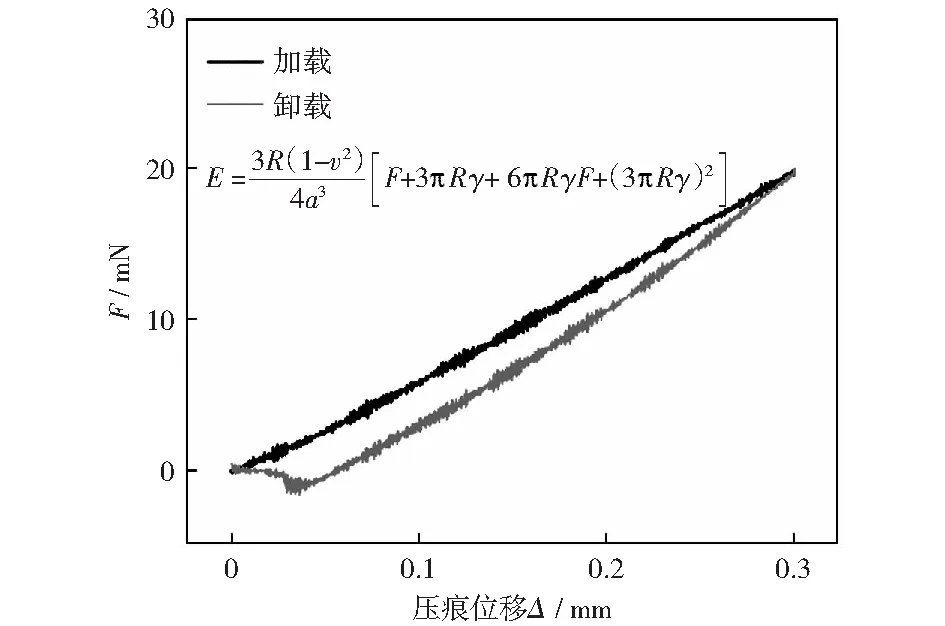
图2 压痕实验数据图Fig.2 Indentation experimental data diagram
1.3 三维应力-应变分析
本文用球对称模型简化描述完整角膜的几何形态(图3),并假设角膜为各向同性材料。根据弹性理论,在球坐标系下,角膜任一点的应力和应变状态可描述为
(2)
式中:i,j=r,θ,φ;r表示径向(即沿厚度方向);θ,φ分别表示相互正交的周向。各向同性角膜的周向应力公式为σθ=σφ=pRc/2t.据图3(c)的受力分析,列平衡方程为
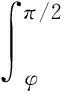
(3)
式中:pI为眼内压(IOP);Rc为角膜的半径;t和t′分别为角膜的整体厚度和任意层厚度。解平衡方程(3),可得径向应力为
将周向和径向应力代入本构方程
(4)
可以得到用于描述完整角膜应变状态的表达式
(5)
式中:E和ν分别为角膜的弹性模量和泊松比。根据文献[14-16],本文将ν值设为0.47、0.40和0.33,以研究泊松比对角膜形变的影响。分析发现完整角膜的应变与角膜厚度有关,本文着重研究角膜5个不同厚度层的应变状态(图3(d)),分别是内表面、外表面以及整体角膜厚度的1/4、1/2、3/4处。
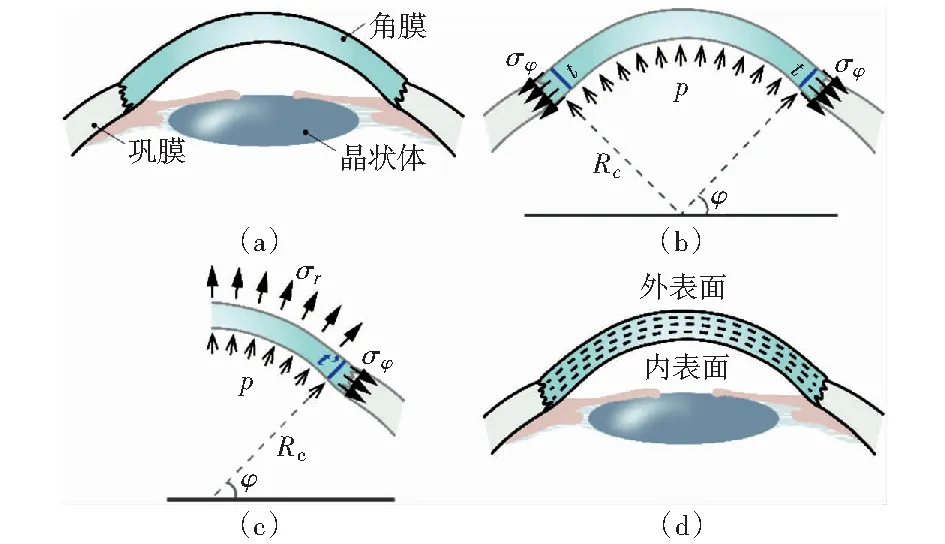
图3 角膜剖面及受力分析示意图Fig.3 Schematic diagram of corneal profile and force analysis
1.4 统计学分析
利用SPSS 17.0分析每组数据的平均值及标准差,实验数据以均值±标准差表示,并行单因素方差分析,P<0.05即认为有显著性差异。
2 结果
2.1 等效弹性模量
本文对宏观压痕实验数据进行JKR分析,获得了不同眼内压下的角膜等效弹性模量值E.发现随着眼内压增加,角膜的等效弹性模量值增加,且在不同的眼内压组之间均存在显著性差异(P<0.05).由压痕实验所得完整角膜的等效弹性模量除了受眼内压的影响外,还与泊松比有关。因此,本文计算了不同泊松比时的角膜等效弹性模量,如表2所示。

表2 角膜的等效弹性模量值(平均值±标准差)Table 2 Equivalent elastic modulus of the cornea (average±SD) kPa
2.2 角膜的三维应变
对周向应变计算与分析(图4)可以看出,周向应变随着角膜厚度的增加而增加,即随厚度的增加呈上升趋势。当泊松比为0.47时,周向应变在0.85%~1.0%范围内,且其总体趋势最低。泊松比为0.33的周向应变在1.1%~1.2%范围内,且其总体趋势最高,泊松比为0.40组的周向应变居中。此外,各个厚度角膜层的周向应变随眼内压的增加呈下降趋势,且高眼压与低眼压之间有显著性差异(P<0.05).
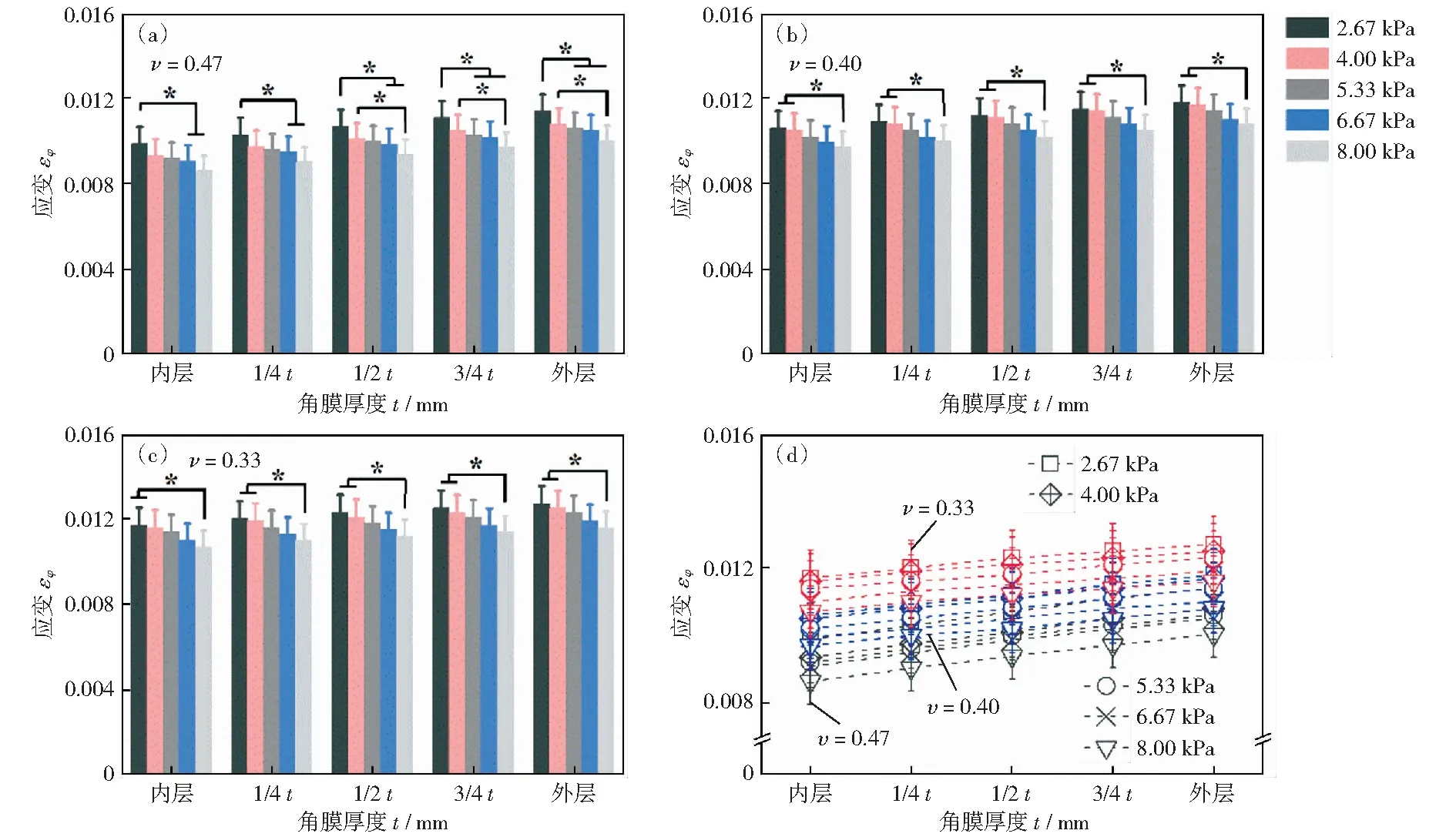
(a)-(c)分别表示泊松比为0.47、0.40以及0.33的周向应变值,(d)为汇总图图4 各生理眼压下不同角膜层的周向应变Fig.4 Circumferential strain of different corneal layers under each IOP
分析不同角膜层的径向应变,结果如图5所示。发现径向应变也随着角膜厚度的增加而增加。泊松比为0.47组的径向应变在-1.5%~-2.0%之间,且其总体趋势最高,泊松比为0.33组的径向应变在-0.75%~-1.0%之间,且其总体趋势最低。泊松比为0.40组的径向应变居中。此外,各角膜层的径向应变随眼内压的增加也呈下降趋势,且高内压与低眼压之间有显著性差异(P<0.05).
获得完整角膜周向和径向应变后,可按ΔV/V=εθ+εφ+εr=2εθ+εr得到角膜的体积应变ΔV/V,进而分析完整角膜对不同眼压的形变响应。分析结果如图6所示,对于完整角膜来说,不同角膜厚度层几乎拥有相同的体积应变。当泊松比为0.33时,所得体积应变值最大,约为1.5%,其次是泊松比为0.40,其体积应变约为0.9%.而体积应变最小时的泊松比为0.47,约为0.3%.与周向和径向应变不同,体积应变几乎不受角膜厚度的影响,但其对泊松比有相对明显的敏感性。
3 讨论
本研究旨在利用压痕实验,获得不同眼内压水平下角膜的等效弹性模量,并用球对称模型分析不同厚度角膜层的三维应变:轴向、径向以及体积应变。文中的等效弹性模量,可以认为是完整角膜在生理眼压下的刚度,描述的是角膜结构水平的力学特性,与单轴拉伸获得材料属性的弹性模量(材料的固有属性,不因其他因素而改变)不同,文中用JKR模型计算得到的等效弹性模量随着眼内压增加而增加,且在不同的眼内压组之间均存在显著性差异(P<0.05)。这与前人研究结果一致,比如WU et al[17]对比正常角膜和高眼压角膜,发现眼压升高,角膜的弹性模量增大,认为其原因是由于眼压升高后,角膜胶原纤维排列方向随机,致单胶原纤维硬化的结果。
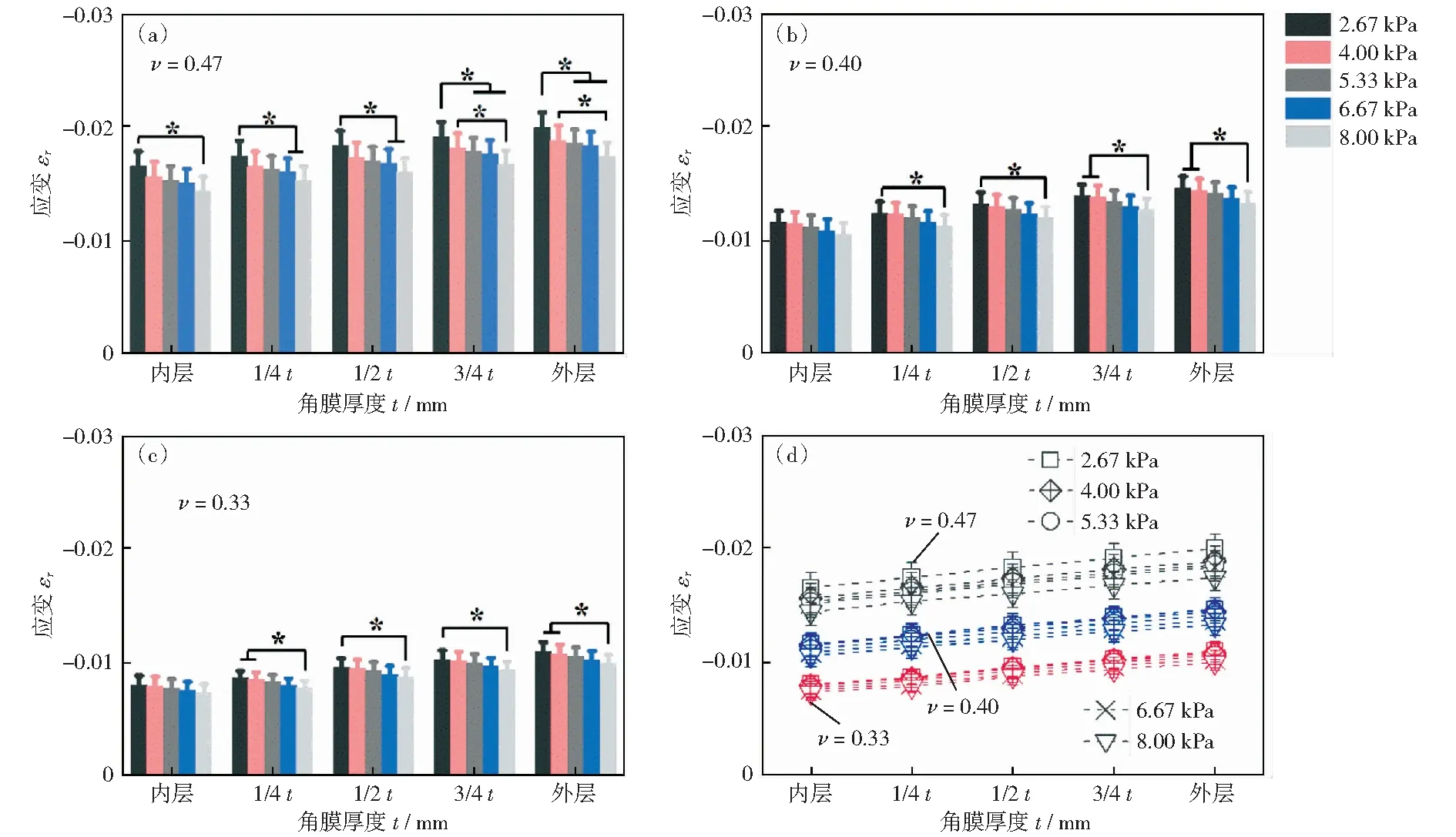
(a)-(c)分别表示泊松比为0.47、0.40以及0.33的径向应变值,(d)为汇总图图5 各生理眼压下不同角膜层的径向应变Fig.5 Radial strain of different corneal layers under each IOP
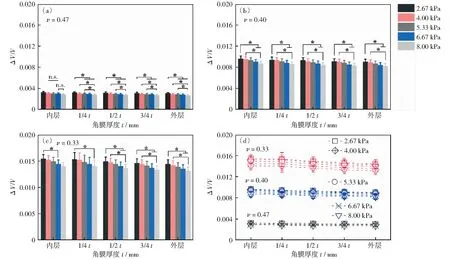
(a)-(c)分别表示泊松比为0.47、0.40以及0.33的体积应变值,(d)为汇总图图6 各生理眼压下不同角膜层的体积应变Fig.6 Volume strain of different corneal layers under each IOP
ZHANG et al[18]利用三维数字图像相关方法测定了角膜外表面在不同眼内压下的应变分布,发现角膜外表面的应变随着眼内压的升高而增加,与本文研究结果一致。对完整角膜在生理眼压的三维应变状态分析表明,完整角膜在周向-径向上存在着拮抗作用。这种拮抗作用可能导致了角膜体积应变的均匀性,即在不同的生理眼压下,完整角膜的体积应变几乎不表现出对角膜厚度的差异化响应。如图4(d)和图5(d)所示,在生理眼压作用下,完整角膜的纤维分别沿周向和径向受拉和受压,且随着角膜厚度的增加,周向和径向应变有同步上升的趋势。从角膜的内表面到外表面,其周向拉伸的变形增量几乎完全被径向压缩的变形增量抵消。在不考虑泊松比的条件下,由于角膜周向-径向应变的拮抗作用存在,导致完整角膜的形变响应对角膜厚度和生理眼压的变化不敏感。
综上所述,角膜的应变在周向-径向间存在着拮抗作用,即在生理眼压作用下,完整角膜的周向应力表现为拉应力,径向应力表现为压应力,这种拮抗作用可能是完整角膜对不同眼压的形变响应呈均匀性的原因。在不同眼内压作用下,随着角膜厚度的增加,周向-径向的拉、压应变同步上升,致角膜从内到外的体积变化均匀。因此,本文着眼于使用数学计算得到不同角膜厚度的三维应变状态,发现不同眼内压下角膜的体积应变基本保持恒定。本文通过研究获得了角膜应变与眼内压、泊松比以及角膜厚度之间的关系,结果有助于进一步定量分析不同的眼内压下角膜的生物力学特性,为今后角膜的力学模型、数值建模提供一定的依据,为进一步深入研究角膜的生物力学特性提供一定的理论参考。
