竖式烧结矿床层内气固体积传热系数实验研究
2021-11-25冯军胜张晟赵亮董辉
冯军胜,张晟,赵亮,董辉
(1.安徽建筑大学安徽省绿色建筑先进技术研究院,安徽合肥,230601;2.东北大学冶金学院,辽宁沈阳,110819)
烧结矿余热资源约占我国钢铁企业余热资源总量的8%,是钢铁企业最具开发潜力的余热资源之一[1-3]。针对现存烧结矿环冷机存在着系统漏风率高、出口热载体品质和余热回收率较低等不足,蔡九菊等[4]提出了一种烧结矿余热竖罐式回收工艺,其吨矿发电量有望比现有环冷机余热发电模式提高70%~80%。目前,烧结矿竖罐仍处于试验研究阶段,竖罐内烧结矿与冷却空气间传热过程是影响烧结矿余热竖罐式回收工艺可行性的关键问题之一。竖罐床层内气固传热决定着烧结矿冷却后的出口温度以及竖罐出口冷却空气的能量品质,从而影响后续空气余热的利用过程[5]。因此,研究烧结矿竖罐内气固传热特性对强化床层内气固传热和提高用能水平都有重要意义。
从床层特点而言,烧结矿余热回收竖罐是一种大颗粒随机填充床。目前,有关颗粒床层内气固传热的研究主要集中在化工领域的反应器、冶金领域的干熄炉、农业领域的干燥器等装置中。LAGUERRE 等[6]研究了在低空气流速下填充床内球形颗粒与壁面之间的传热过程,并给出可以预测床层内气固对流传热系数的关联式。PEŠIĆ 等[7]研究了填充床内高温球形颗粒与较大冷球体间的传热过程,分析了颗粒粒径、冷球体直径和气体流速对填充床内传热系数的影响,并确定了床层内整体传热系数的关联式。ZHANG 等[8]研究了颗粒填充床与相邻壁面间的传热过程,提出了一个床层与壁面的传热模型及模型参数,并通过参数综合灵敏度分析,得出颗粒温度、颗粒停留时间和颗粒粒径是床层传热系数的临界参数。CONG等[9]研究了壁面恒热流条件下填充床反应器内气固传热过程,并采用对数平均温差法获得床层内总传热系数关联式。KAMATH 等[10]研究了竖直通道内空气与金属多孔介质之间的换热过程,并给出了雷诺数在1 000~7 000 范围内的传热关联式。KURTBAS等[11]研究了在矩形通道内流体与不同空隙率的金属多孔介质强制对流的传热特性,并基于实验数据,得出了气固传热经验关联式。YANG等[12-13]研究了非球体颗粒填充床内气固传热特性,指出颗粒为球体与椭球2种情况下气固传热规律是不同的,并通过实验给出修正后的气固传热关联式。VISKANTA 等[14]研究了空气与蜂窝陶瓷间气固换热过程,并给出气固体积传热系数的实验关联式,解决了气固换热面积无法精确计算问题。冯妍卉等[15-16]推导出了焦炭床层平均体积换热系数公式,研究了焦炭粒度、冷却气体流量对干熄炉内焦炭换热的影响,并得到了焦炭床层内平均体积换热系数关联式。
综上所述,目前有关气固传热系数的研究主要集中在均匀或球形颗粒床层中,且实验所得关联式以颗粒床层内气固面积传热系数为主。由于烧结矿是一种非均匀不规则颗粒,其床层内气固传热面积难以精确计算,而有限研究所得实验关联式[14-16]并不适用于求解烧结矿床层内气固传热过程。基于此,本文作者在自制气固传热实验装置上,研究烧结矿床层内气固体积传热系数的主要影响因素及其规律,并通过实验数据拟合得出床层内气固体积传热系数的关联式,旨在为烧结矿竖罐内气固传热数值计算和参数优化提供参考。
1 实验装置及方法
1.1 实验装置
烧结矿床层内气固传热实验装置由鼓风机、调节阀、流量计、测温孔、实验竖罐本体等部件组成,实验装置示意图如图1所示。
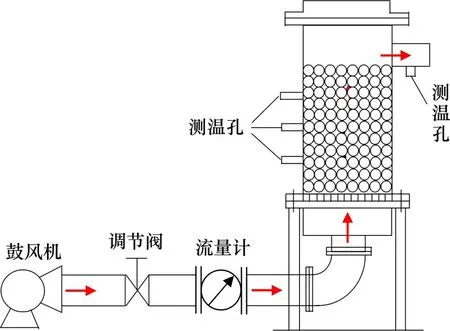
图1 气固传热实验装置结构示意图Fig.1 Schematic diagram of gas solid heat transfer experimental setup
实验装置内横截面为圆形,内径为0.45 m,在装置内壁四周填充保温材料,以减少装置内部的热散失。实验工况下装置内烧结矿床层高度均为0.6 m,在床层高度为0.1,0.3和0.5 m处设测温孔用来测量床层内烧结矿温度,空气出口处设有测温孔用来测量空气出口温度。实验用烧结矿是经环冷机处理后的成品烧结矿,通过标准筛筛分后的烧结矿颗粒参数[17-19]如表1所示,其中,颗粒当量直径为颗粒平均直径与颗粒形状因子的乘积。

表1 筛分后烧结矿颗粒参数Table 1 Parameters of sieved sinter particles
1.2 实验过程
烧结矿经加热炉升温至700~800 ℃后装入实验装置内,待装置内烧结矿温度均匀稳定后打开鼓风机,冷却空气在风机驱动下先后通过调节阀、流量计和烧结矿床层,最后从装置顶部排出。
首先,测量烧结矿在装置内的初始温度,然后调整空气阀门使得空气流量到达某一设定值,空气流量通过流量计测得,同时开始计时,每隔一段时间,采用K-type (Ni/Al)型热电偶对不同床层高度处的烧结矿温度进行测量,并采用抽气式热电偶对装置出口处空气的温度进行测量,直至装置出口处空气温度接近环境温度为止。重复以上实验过程,得出不同空气流量和烧结矿颗粒直径条件下床层内烧结矿温度和空气出口温度的变化规律,进而分析影响烧结矿床层内气固体积传热系数的主要因素及其影响规律。在实验结果处理中,以烧结矿颗粒当量直径作为特征长度,以不同床层高度处的烧结矿温度的平均值作为装置内烧结矿温度,以冷却空气进出口温度的平均值作为定性温度。
1.3 实验方法
根据床层内气固传热方程可知,在dτ时间内,冷却空气在烧结矿床层微元段dV内的换热量为
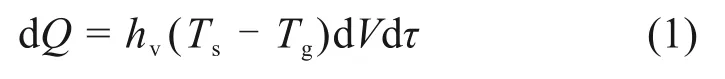
式中:Q为气固换热量,J;hv为气固体积传热系数,W/(m3·K);Ts为床层内烧结矿温度,K;Tg为冷却空气温度,K;V为床层内烧结矿堆积体积,m3;τ为换热时间,s。
根据能量守恒定律可得,在dτ时间内,微元段内烧结矿和冷却空气的温度变化分别为:

式中:ρs为烧结矿的密度,kg/m3;ε为床层空隙率;cs为烧结矿的比定压热容,J/(kg·K);cg为空气的比定压热容,J/(kg·K);v为床层内空气表观流速,m/s;A为床层的横截面积,m2。
式(2)与式(3)相减可得
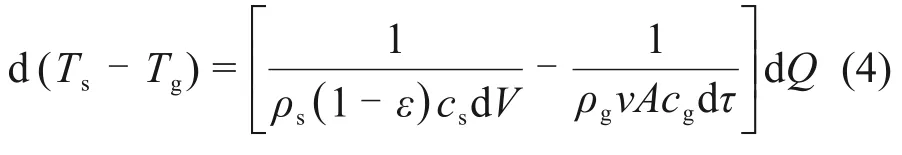
将式(1)代入式(4),经整理得
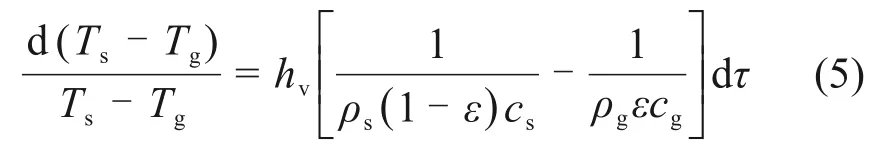
将式(5)两边积分可得
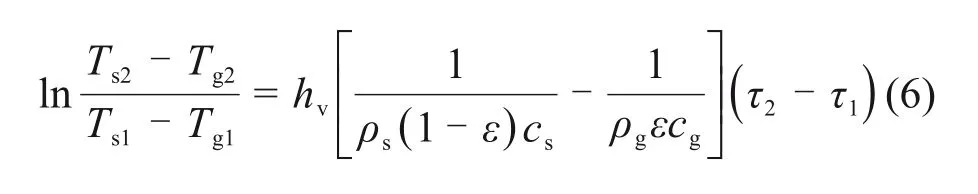
式中:Ts1和Tg1分别为τ1时刻床层内烧结矿温度和空气温度,K;Ts2和Tg2分别为τ2时刻床层内烧结矿温度和空气温度,K。
由此得出烧结矿床层内气固体积传热系数计算公式为
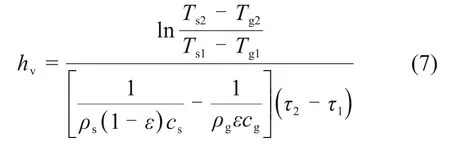
床层内气固体积传热Nusselt数的计算公式为

式中:Nuv为体积传热Nusselt数;dp为烧结矿颗粒当量直径,m;λg为空气导热系数,W/(m·K)。
在实验过程中,分别对不同烧结矿颗粒直径和空气进口流量条件下的工况进行测试,得出不同工况在不同时刻的床层烧结矿温度和空气温度,并采用式(7)和式(8)计算出不同实验工况下床层内气固体积传热系数和Nusselt数。
2 实验结果与分析
在实验结果处理中,烧结矿和空气的物性参数[20-21]取值如表2所示。
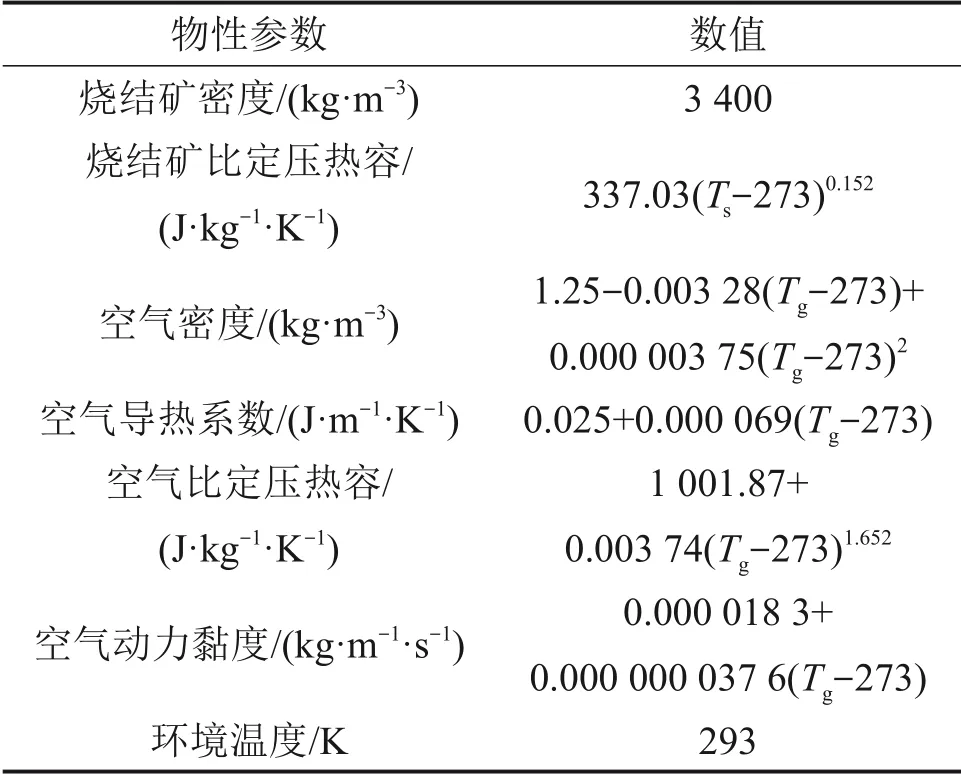
表2 烧结矿和空气物性参数Table 2 Physical parameters of sinter and air
2.1 影响因素分析
通过测量不同烧结矿颗粒直径下床层内颗粒温度和空气出口温度,得出了空气进口流量为600 m3/h条件下床层内气固体积传热系数随颗粒直径的变化示意图,如图2所示。由图2可知:当床层内颗粒直径一定时,床层内气固体积传热系数随颗粒温度升高逐渐增大。这是因为床层内颗粒温度越高,同位置处对应的空气温度也越高,此时床层内空气表观流速也越大,空气与烧结矿颗粒之间的换热强度会增强,床层内气固体积传热系数随之增大。
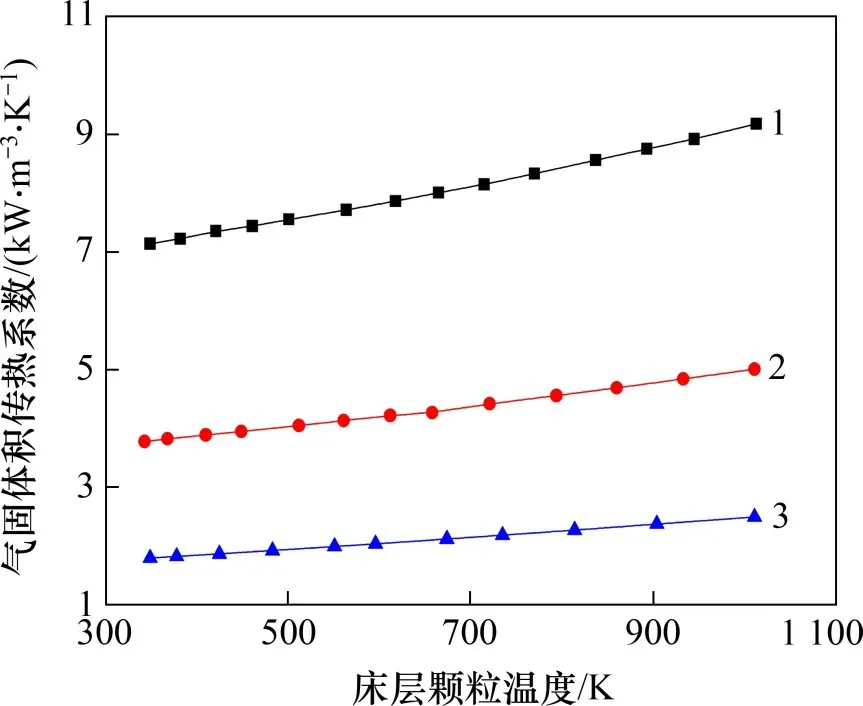
图2 烧结矿颗粒直径对床层内气固体积传热系数的影响Fig.2 Effect of sinter particle diameter on gas solid volumetric heat transfer coefficient in bed layer
当床层内颗粒温度一定时,烧结矿颗粒直径越小,床层内气固体积传热系数也就越大。这是因为烧结矿颗粒直径越小,颗粒比表面积越大,并且同位置处空气温度越高,空气与烧结矿颗粒的换热强度也会增强,这就会导致床层内气固体积传热系数增大。
图3所示为烧结矿颗粒直径为18 mm条件下床层内气固体积传热系数随空气进口流量的变化示意图。由图3可知:当床层内颗粒温度一定时,空气进口流量越大,床层内气固体积传热系数也越大。这是因为空气进口流量增加将会导致床层内空气表观流速增加,空气与烧结矿颗粒之间的换热强度就会增强,床层内气固体积传热系数也就随之增大。
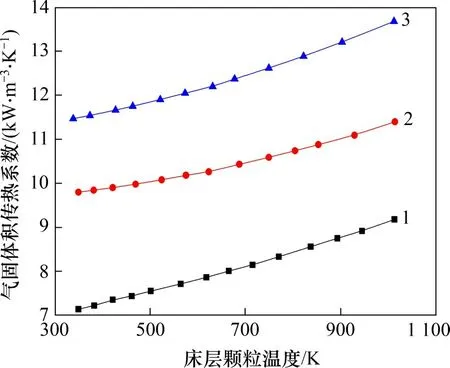
图3 空气进口流量对床层内气固体积传热系数的影响Fig.3 Effect of air inlet flow rate on gas solid volumetric heat transfer coefficient in bed layer
2.2 关联式拟合
目前,RANE 等[22-25]已提出了计算颗粒床层内气固传热系数的经验关联式,如表3所示。其中,RANZ等[22,25]得到床层内气固面积传热Nusselt数关联式,而BIRD 等[23-24]得到床层内气固体积传热Nusselt数关联式。采用表3中几种经验关联式分别计算烧结矿颗粒直接为27 mm 条件下床层内气固体积传热Nusselt 数,所得计算值与实验值的对比关系如图4所示。经验关联式的计算平均相对误差η采用如下公式进行计算:
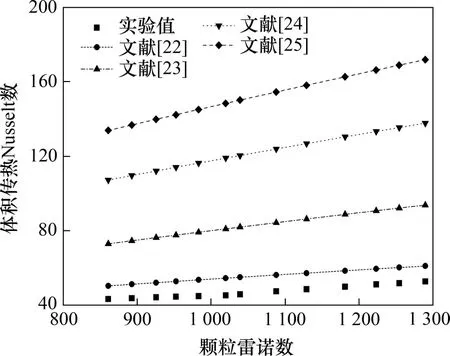
图4 颗粒直径为27 mm床层内Nusselt数实验值与计算值的对比Fig.4 Comparison between experimental data and calculated values of Nusselt number in bed layer for d=27 mm
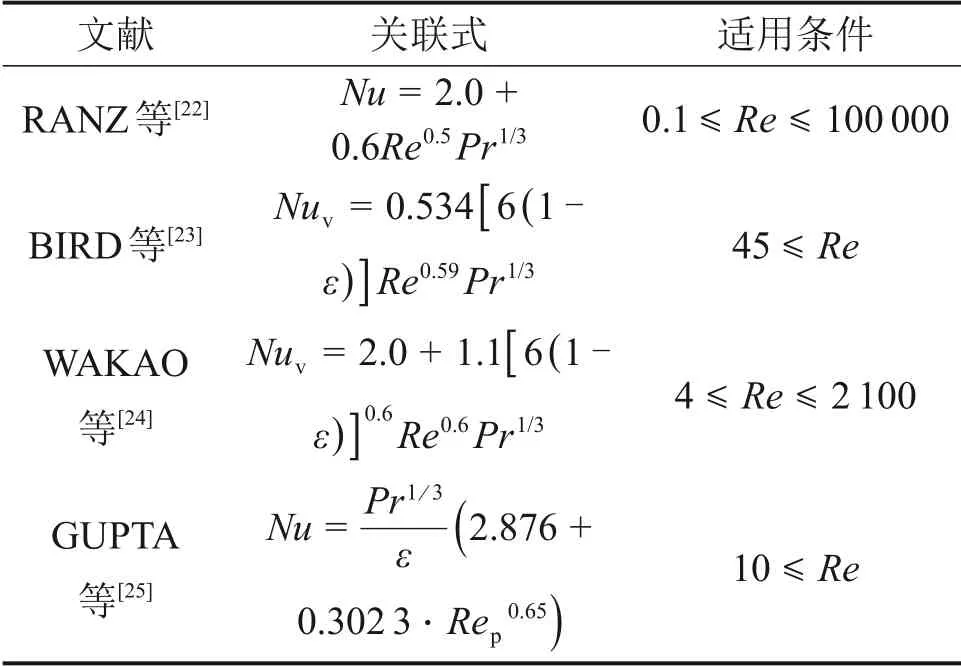
表3 填充床内气固传热系数关联式Table 3 Correlations of gas solid heat transfer coefficient in packed beds
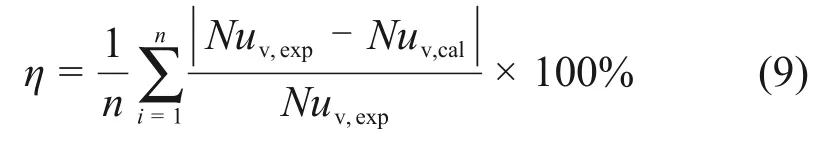
式中:Nuv,exp为实验测得的Nusselt数;Nuv,cal为计算所得的Nusselt数;n为实验次数。
从图4可知:根据BIRD 等[23-25]中经验关联式计算得到的床层内体积传热Nusselt 数与实验值相差较大,平均相对误差均超过50%。采用RANZ等[22]提出的关联式计算所得的体积传热Nusselt 数与实验值相差相对较小,平均相对误差为17.76%,而基于整个实验工况,RANZ等[22]提出的关联式的平均误差也达到20.88%。因此,表3中描述颗粒床层内气固传热的经验关联式不适用于计算烧结矿床层内的气固传热过程。
RANZ等[22]提出的关联式的Nusselt数计算值随颗粒雷诺数的变化幅度与实验值的变化基本一致,因此,描述烧结矿床层内气固体积传热系数的关联式可设定为如下形式:
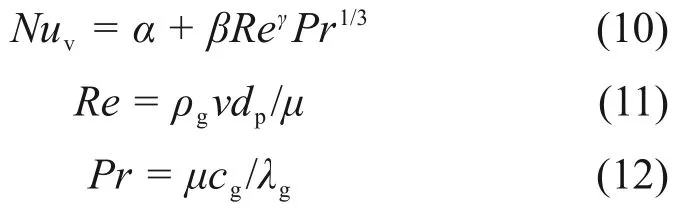
式中:α,β和γ分别为实验常数,可通过实验数据拟合获得;Pr为普朗特数,m/s;μ为空气动力黏度,kg/(m·s)。
通过对式(10)进行变换,且两边取对数可得如下线性方程:
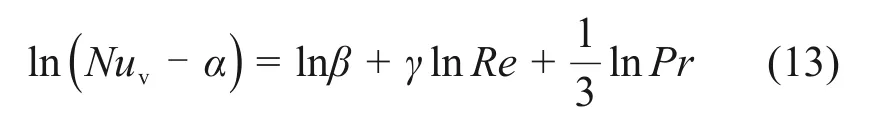
利用最小二乘法,将实验数据代入式(13),同时设定α为不同数值,并对式(13)进行线性回归计算,可得不同α条件下β和γ的具体数值,如表4所示。
从表4可知:当α为5 时,采用实验数据拟合所得关联式的平均相对误差和最大相对误差均最小。描述烧结矿床层内气固体积传热系数的关联式为
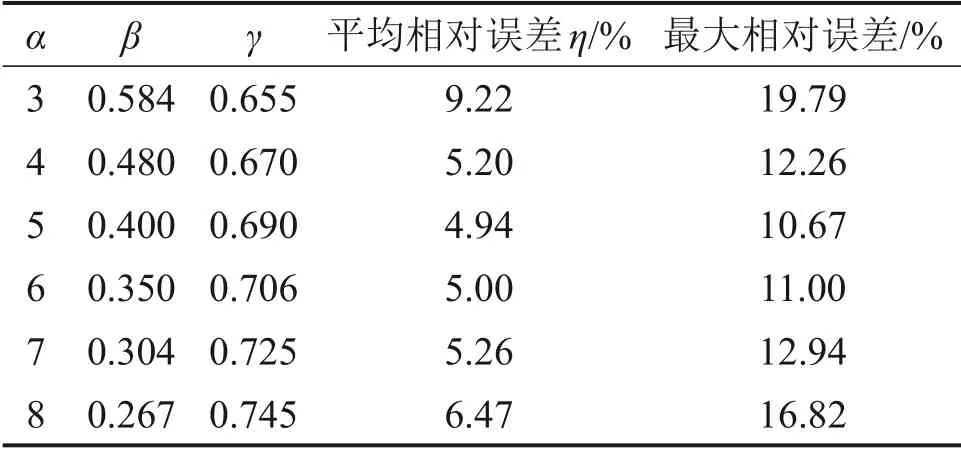
表4 不同α条件下β和γ的具体数值Table 4 Specific values of β and γ with different α
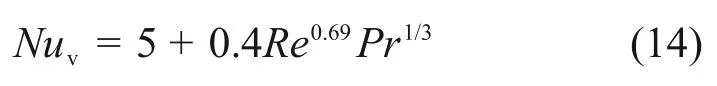
式中:540≤Re≤3724。
图5所示为采用式(14)计算所得床层内气固体积传热Nusselt 数计算值与实验值之间的对比关系图。由图5可看出:采用式(14)计算所得床层内气固体积传热Nusselt 数与实验值能较好吻合。结合表4可知,对于整个实验工况,由式(14)所得Nuv的平均相对误差η为4.94%,最大相对误差为10.67%。因此,式(14)可适用于计算烧结矿床层内气固传热过程。
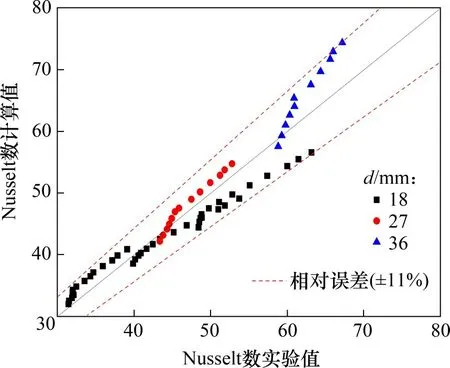
图5 Nusselt数拟合实验关联式实验值与计算值的对比Fig.5 Comparison between experimental data and calculated values of fitting experimental correlation of Nusselt
3 结论
1)烧结矿颗粒直径和空气进口流量是影响烧结矿床层内气固传热过程的主要因素。烧结矿颗粒直径越小,空气进口流量越大,床层内气固体积传热系数也越大。另外,当颗粒直径和空气进口流量一定时,床层内颗粒温度越高,气固体积传热系数越大。
2)由于计算误差较大,已有颗粒填充床层内气固传热的Nusselt 数关联式不适用于计算烧结矿床层内气固体积传热系数。采用实验数据拟合确定的Nusselt 数关联式能很好地描述烧结矿床层内气固传热过程,其平均计算相对误差仅为4.94%。
3)与现有床层内气固传热Nusselt 数关联式相比,本文所得实验关联式能解决非均匀烧结矿床层内气固传热面积难以精确计算的问题,同时不需要考虑床层空隙率的影响。
