含软弱结构面岩体蠕变力学模型

赵晨阳，雷明锋,2，贾朝军，张逆进，彭龙，龚琛杰

（1.中南大学土木工程学院，湖南长沙，410075；2.重载铁路工程结构教育部重点实验室，湖南长沙，410075；3.中铁十二局集团第七工程有限公司，湖南长沙，410029；4.中交三航局第三工程有限公司，江苏南京，210011）

岩土体流变是影响隧道长期稳定的重要因素之一[1-3]，主要包括蠕变、松弛、长期强度和弹性后效，其中蠕变是主要研究内容[4]。隧道与地下工程的实践与研究均表明，开挖区域围岩的破坏可能在开挖后几天甚至几年发生。为探究岩石蠕变特性，科技工作者从岩石蠕变力学试验出发，对试验数据进行拟合得到经验公式，建立岩石的应力、应变与时间的函数关系式。该方法虽然反映了某种岩石在设定条件下的蠕变特征，但并未反映其内在机理。为此，将元件模型引入岩石蠕变特性研究领域，并用于分析岩石的长期稳定性。为解决元件组合模型不能反映岩石流变的非线性问题，学者们对元件模型进行了改进，或采用内时理论[5]、损伤力学[4]、断裂力学[6]等新理论建立岩石蠕变本构模型，如：徐卫亚等[7-8]在进行绿片岩三轴流变力学试验的基础上，将非线性黏性元件与黏弹性元件串联起来，建立了河海模型；韦立德等[9]从岩石蠕变机理出发，建立了由非线性元件组成的一维黏弹塑性模型来反映岩石流变全过程；周家文等[10]通过构造非线性函数并引入广义Bingham 模型，建立了非线性蠕变模型；张贵科等[11]建立了一个与应力状态和时间相关的非线性黏性体，并将该非线性黏性体与传统Maxwell模型相结合，建立了五元件黏弹塑性模型；杨春和等[12]结合盐岩流变试验，采用岩石损伤力学理论研究了盐岩流变损伤特征，并建立了非线性流变本构模型；贾善坡等[13]通过构造基于摩尔-库仑准则的蠕变势，建立了泥岩非线性蠕变损伤本构模型及其损伤演化方程；ZHU 等[14]基于细观力学推导Eshelby 等效加载问题的均匀化理论，在热力学框架下得到了准脆性岩石各向异性的弹塑性损伤本构模型。

综合上述分析可知，岩石蠕变模型已取得一些研究成果，但适用于软弱结构面岩体的非线性蠕变元件本构模型理论的研究仍处于初级阶段，有待深入研究。随着川藏铁路、跨江（海）隧道等重大工程的建设，为避免围岩流变对隧道施工及运营产生较大影响，对含软弱结构面岩体的蠕变力学特性理论研究就显得十分迫切和重要[15-17]。为此，本文基于Kachanov-Rabotnov 理论建立考虑蠕变抗剪强度的非线性黏塑性元件，进而结合Burgers 模型建立考虑软弱结构面的岩石流变力学模型，并通过相关试验验证模型的合理性，该成果可为隧道长期稳定分析提供理论依据。

1 加速蠕变模型

1.1 蠕变变形特征

在长期荷载作用下，含软弱结构面岩体的变形具有明显的时效性。在恒定应力作用下，岩石蠕变的理论曲线如图1中曲线a所示。

图1中，OM段对应加载瞬间产生的弹性应变；MN段对应应变速率随时间增长而逐渐递减的初期蠕变阶段，亦称衰减蠕变阶段；NP段对应应变速率随时间增长呈稳定状态的第二期稳态蠕变阶段，亦称等速蠕变阶段，此阶段的历时主要取决于应力水平和加载速率；PQ段对应试件达到破坏前应变速率呈加速增长的第三期蠕变阶段，称为加速蠕变阶段。

岩体蠕变曲线的形状因岩体属性、应力状态以及环境条件产生差异。

1）当应力水平低于某一限值时，岩体几乎不产生蠕变，如图1中曲线b所示。

2）当应力水平较高且接近岩石的强度时，蠕变3个区段的区分度可能不明显，表现为变形急剧发展直至试样破坏，如图1中曲线c所示。

图1 恒定应力作用下的蠕变曲线Fig.1 Creep curves under constant stress

3）当应力水平较低时，可能只产生衰减蠕变和稳态蠕变，即曲线a 上的MN和NP这2 个蠕变阶段。

1.2 加速蠕变的描述

为克服既有元件组合模型（如Burgers 模型和Nishihara模型）无法充分描述加速蠕变特征的不足，本文提出一种新的蠕变本构模型。根据不连续点在加速蠕变阶段之前没有明显的非线性蠕变变形，假设岩石在加速蠕变阶段前未受到破坏，即在加速蠕变阶段前的损伤变量D为0，试样破坏时的损伤变量D为1.0。

RABOTNOV[18]提出的Kachanov-Rabotnov理论可用于描述损伤的演变：

蠕变本构方程为

式中：σ为应力；为蠕变变形（εc）对时间的微分；m，n，p，q，A和B均为材料常数。

根据式（2），无损伤的含软弱结构面岩石试样的蠕变应变可写为

式（3）表明，不同剪应力水平下的稳态蠕变速率可以采用幂函数表示。

在恒定应力下，加速蠕变阶段损伤D可以通过对方程（1）进行积分确定。假定t=0时刻边界条件D=0，可得

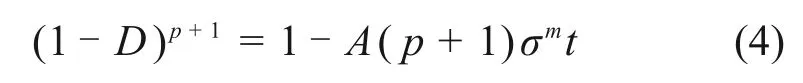
需注意的是，初始时间是加速蠕变的开始时间。

进一步假定试样蠕变破坏的时间t=tR，此时，试样损伤值D=1.0，将此边界条件代入式（4）得

将式（5）代入式（4），得到损伤变量D：

由式（6）可知，损伤变量D随时间变化，并将其代入式（2）并积分，可得蠕变随时间的变化。假定t=0时刻εc=0，可得

式中：λ=(1+p)/(1+p-q)，其为1个大于1.0的常数，与材料性质有关。

由式（7）可知，将t=tR代入，可得试样破裂时的蠕变应变：

式（8）表示的蠕变应变如图2所示。从图2可以看出：若试样未发生加速蠕变变形，则蠕变变形为稳态蠕变速率与时间的积，而若试样发生加速蠕变，则蠕变变形需要乘以材料常数λ。

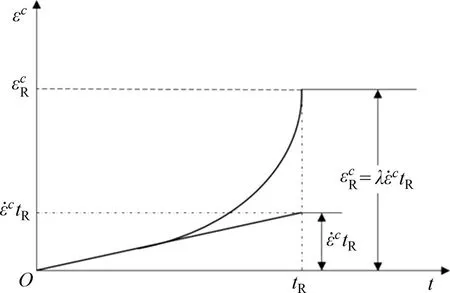
图2 蠕变应变随时间变化的示意图Fig.2 Schematic diagram of creep strain change with time

1.3 参数敏感性分析

为分析剪应变与材料常数λ的关系，对λ的参数敏感性进行分析。设定式（8）中=1×10-4h-1，tR=0.7 h，得到不同λ条件下的蠕变-时间曲线如图3所示。从图3可以看出：λ越大，剪应力和剪切速率越大；当λ为1.0 时，蠕变应变在整个过程中呈线性增大。

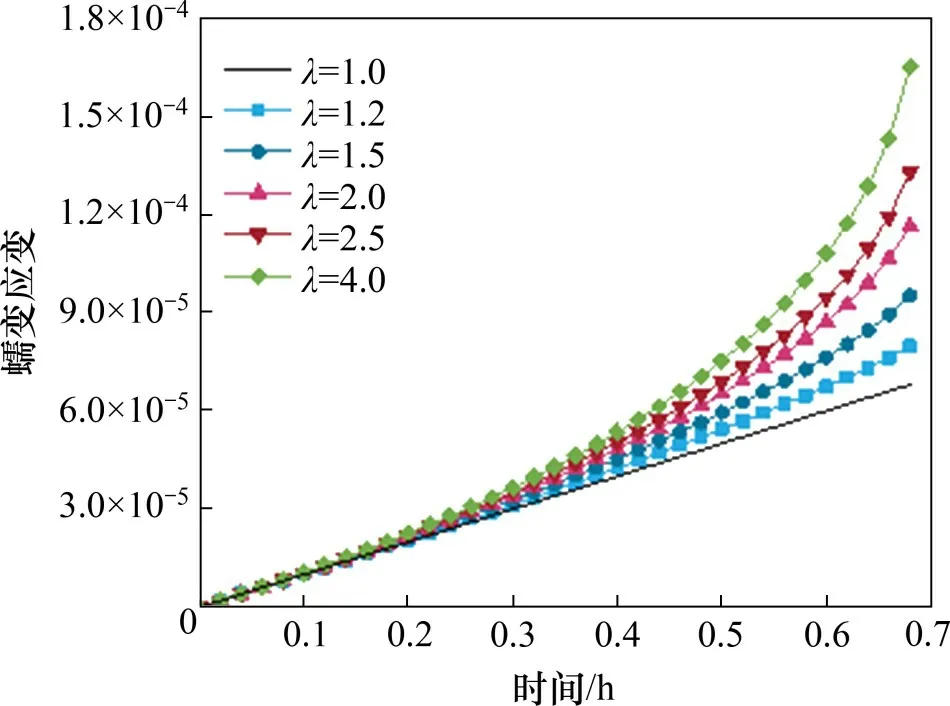
图3 参数λ对蠕变应变的敏感性分析Fig.3 Sensitivity analysis of the parameter λ to creep strain

式（7）描述了加速蠕变阶段的非线性蠕变规律。考虑到在多级剪切蠕变试验中，加速蠕变阶段仅在最终剪切应力水平下发生，并且与该阶段的稳态应变率有关，故式（7）可变化为

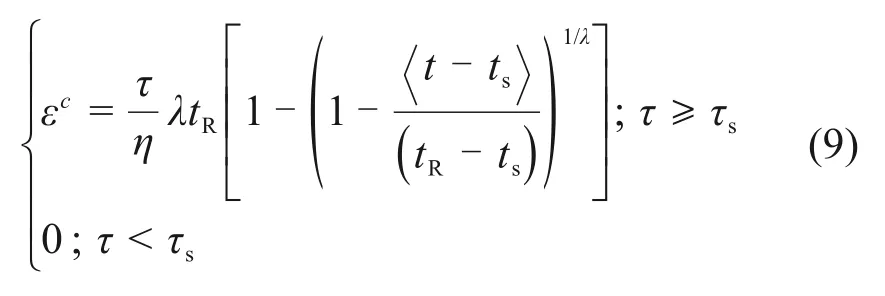
式中：ts为含软弱结构面岩体进入加速蠕变阶段的时间；η为黏度系数；·为麦考利符号，x=(x-|x|)/2。

根据式（9），可得到非线性加速蠕变元件，见图4。当剪切应力小于阈值τs时，非线性加速蠕变元件不工作；当应力大于阈值τs时，蠕变应变将随时间呈非线性增加。

图4 非线性加速蠕变元件示意图Fig.4 Schematic diagram of nonlinear accelerated creep element

2 蠕变模型

2.1 Burgers蠕变特征

Burgers 蠕变模型是一个线性黏弹塑性流变模型，可以较好地描述岩石的瞬时弹性变形、初期流变变形与稳态流变变形，同时能反映岩石的松弛现象。Burgers 流变模型可认为是Maxwell 模型与Kelvin 模型的组合体，一维应力状态下的流变模型如图5所示。

图5 Burgers蠕变模型Fig.5 Burgers creep model

在外荷载长期作用下，当切应力为τn时，Burgers流变模型相应的状态方程为

式中：τ1和τ2为切应力；G1和G2分别为Maxwell模型和Kelvin 模型的体积模量；ε11，ε12和ε2分别为Maxwell模型中弹性虎克元件、黏性牛顿元件和Kelvin 模型的应变；和为应变率；η1为Maxwell 模型黏度系数；η2为Kelvin 模型黏度系数。

根据式（10），消去方程中的下标可得系统总应力、应变本构方程为

在t=0 时，施加恒定应力τn，将τn代入式（10），同时考虑下列初始条件：

式中：i=1，2。对式（10）进行拉普拉斯变换及其逆变换，可得蠕变方程：

将式（13）两边分别对时间t求一阶、二阶导数可得：

由式（14）和式（15）可知＞0，而¨＜0。施加恒定应力τn后，模型产生瞬时弹性变形及蠕变变形，且随着时间增加，蠕变速率逐渐减小，最终达到稳定。

2.2 非线性6元件蠕变本构模型

为全面描述含软弱结构面岩体的蠕变特性，将非线性元件和Burgers 蠕变模型串联在一起，可得1个六元件非线性黏弹性塑性不连续模型，如图6所示。

图6 改进的6元件非线性黏弹塑性蠕变模型Fig.6 Improved nonlinear visco-elasto-plastic creep model for 6 elements

与Burgers 模型相比，其适用于非线性元件的加速蠕变特性。该模型的本构方程为

式中：η3为加速蠕变规律非线性模型黏度系数。

3 蠕变模型验证

为验证本文提出非线性黏弹性塑性蠕变模型的合理性，制取软弱结构面试样，在不同应力等级下开展多级蠕变试验。

剪切蠕变试验在CSS-3940YJ 型岩石伺服控制双轴流变试验机上进行。多级剪切蠕变试验流程与文献[19]中断层F17的试验流程相同。本次模型验证共完成3个试样的试验，在3个试样上分别施加0.2，0.6 和1.0 MPa 的正应力σn。具体的试验步骤如下：1）施加正应力至设定值；2）以位移控制模式（0.2 mm/min）施加剪切应力，每种应力水平维持约48 h 或72 h；3）待试样在该级正应力下达到稳态蠕变阶段后继续施加下一级剪应力；4）若剪切位移以大于阈值的速率增加或样品失败，则停止记录数据，并且结束测试。

试验所得到的剪切位移随时间变化曲线如图7和图8所示。分析图7和图8可见：

图7 不同正应力下剪切蠕变曲线Fig.7 Shear creep curves under different normal stresses

图8 最后一级剪应力下的蠕变和蠕变速率曲线Fig.8 Creep and creep rate curves under the last shear stress

1）在施加每级荷载时都会产生瞬时弹性应变，随后经历衰减蠕变阶段，蠕变速率随时间逐渐降低。

2）当剪切应力水平较低时，剪切蠕变速率减小至恒定值，意味着剪切变形呈线性增加，即试件处于稳态蠕变阶段。

3）当剪应力加载到最后一级时，经过稳态蠕变后的试样蠕变速率迅速增加，蠕变变形也急剧增加并最终导致试样破坏。

运用建立的模型对实验数据进行拟合，拟合后各参数如表1所示。表中，R2为可决系数。分析表1可知：

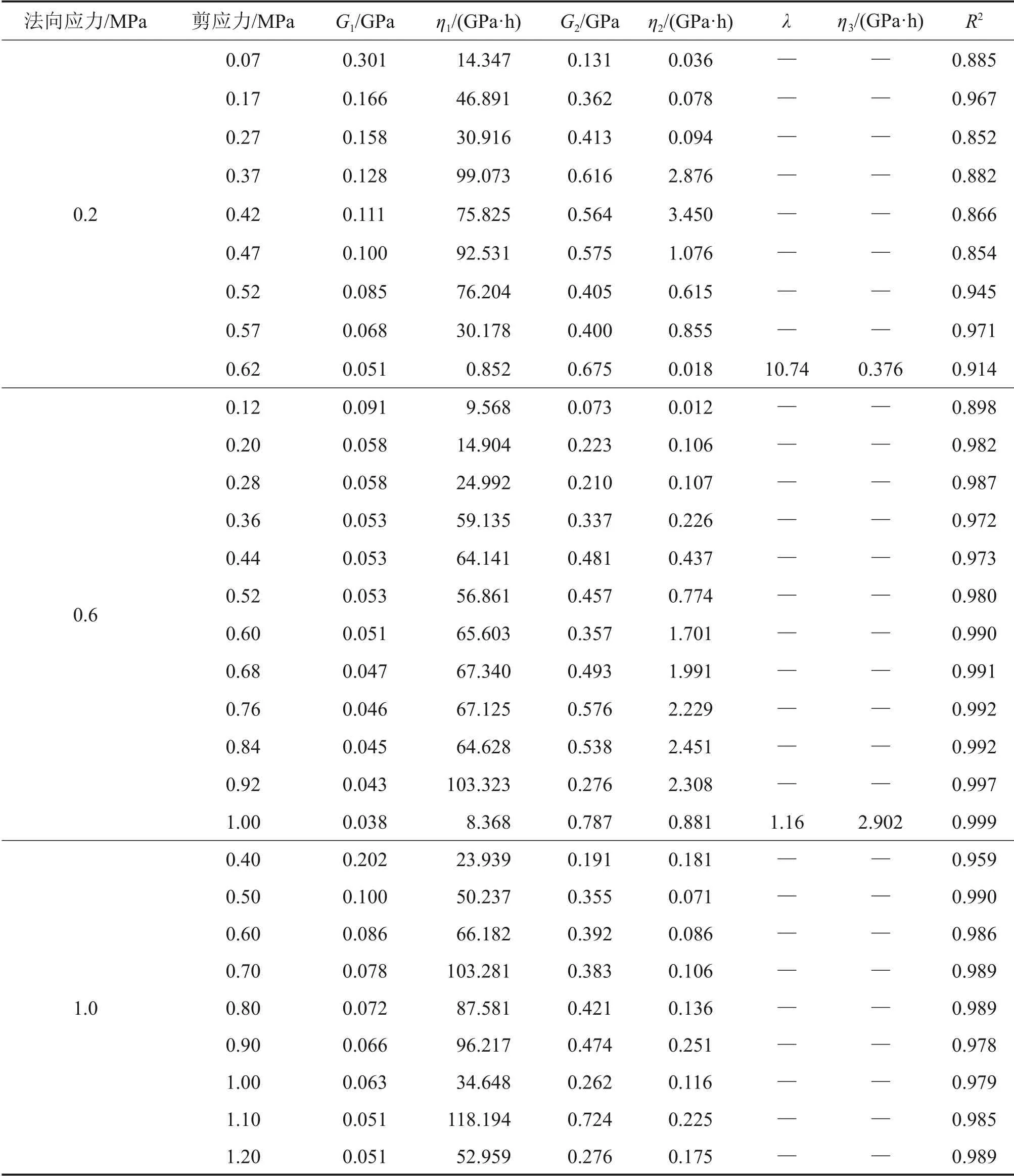
表1 蠕变模型拟合参数的结果Table 1 Results of creep model fitting parameters

1）在恒定法向应力下，体积模量初始阶段的G1远比其他剪应力时的高，并随剪应力增加而减小。

2）忽略初始值时，G1和剪切应力间的关系可用线性方程式描述（图9）。法向应力分别为0.2，0.6，1.0 MPa的3个样品的体积模量G1的平均值分别为0.43，0.36和0.39 GPa。

图9 拟合体积模量G1与剪切应力之间的关系Fig.9 Relationship between fitted volume modulus and shear stress level

3）通常，黏度系数η1随剪切应力增加而增加，这与稳态蠕变结果相吻合。

4）G1/η2反映了从初始蠕变阶段到稳态蠕变阶段的持续时间，其随着剪切应力的增加而趋于减小。

最终阶段的拟合曲线如图10所示。从图10可见所提出的模型能够描述软弱结构面的加速蠕变阶段的变形特性。

图10 剪切蠕变模型的拟合效果Fig.10 Fitting effect of shear creep model

4 结论

1）基于Kachanov-Rabotnov 蠕变损伤理论开发了非线性元件，并将该非线性元件和Burgers 蠕变模型串联起来形成六单元非线性黏弹性塑性蠕变模型，可以实现含软弱结构面岩体的加速蠕变阶段模拟。

2）试样在衰减蠕变阶段的蠕变速率随时间逐渐降低。当剪切应力水平较低时，剪切蠕变速率减小至恒定值，处于稳态蠕变阶段。随着剪应力增加，经过稳态蠕变后的试样蠕变速率迅速增加，蠕变变形亦急剧增加并最终导致试样破坏。

3）所提出的模型能够描述不连续性的时间相关特性，可以对试样软弱结构面剪切蠕变特性进行较全面描述。