连接体当中的临界问题

戴 辉

(福建省清流县第一中学 365300)

连接体中的临界问题，在运用牛顿第二定律解题时很常见，处理问题时关键是分清问题的实质，关注隐含问题的分析.

一、物体与斜面间的弹力存在临界

例1如图1，质量为M的斜劈通过一根平行于斜面的轻质绳系着一个质量为m的小球(可视为质点)，若通过外力作用使得它们一起向右做匀加速直线运动，加速度是a，求斜劈及轻绳对小球的支持力N、拉力F的大小.

思路点拨本题主要考查对牛顿第二定律的理解应用能力、分析推理能力及临界条件的挖掘的能力.

我们同学在解决这类问题时经常出现的错解主要在于：对物理过程缺乏清醒认识，不会用极限分析法挖掘题目隐含的临界状态及条件，使问题难以切入.

解析对小球进行受力分析，如图2所示，小球受到重力G、轻绳的拉力F、斜劈的支持力N，进行正交分解，满足：

Fcosθ-Nsinθ=ma

①

Fsinθ+Ncosθ=mg

②

解得：F=m(gsinθ+acosθ)

N=m(gcosθ-asinθ)

解析方法点拨：上面①、②式中解出F、N的方法、技巧，①×cosθ+②×sinθ得出拉力F的大小，②×cosθ-①×sinθ得出支持力N的大小——解此类二元一次方程的常用方法.

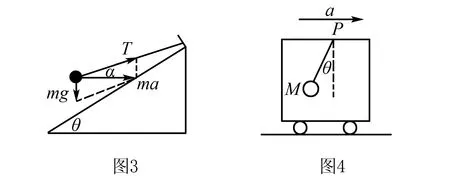
解后反思解题方法与技巧：当加速度a较小时，小球与斜面体一起运动，此时小球受重力、绳拉力和斜面的支持力作用，绳平行于斜面，当加速度a足够大时，小球将“飞离”斜面，此时小球受重力和绳的拉力作用，绳与水平方向的夹角未知，题目中要求必须先求出小球离开斜面的临界加速度a0与题设所给的加速度a进行比较分析判断(此时小球所受斜面支持力恰好为零).

比如如图4所示的例题：小车在水平面上，一根轻绳一端固定于小车的顶端，另一端系着一个可视为质点的小球.若小车在水平面上做加速度为a的匀加速直线运动.求稳定时轻绳与竖直方向的夹角及拉力F的大小.

二、物体与水平间的弹力存在临界

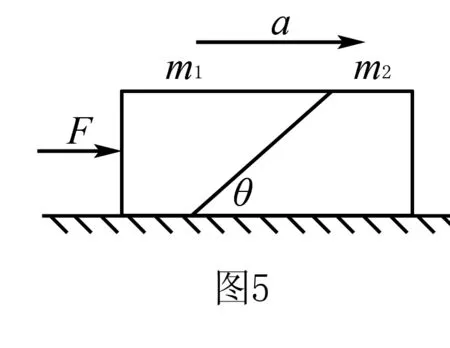
例2 如图5所示，质量为m1、m2的两个物体，中间接触面与水平面夹角为θ且光滑，它们与地面之间的动摩擦因数均为μ.现用水平力F推m1物体，使得m1、m2的两个物体一起向右匀加速直线运动，加速度为a(a未知).求水平推力F的最大值.

思路点拨由于m1、m2的两个物体一起向右匀加速直线运动，故此本题也属于面接触连接体问题.处理方法仍然是：整体法求加速度，隔离法求m1、m2的两个物体之间的相互作用力，再分析力F的变化引起在接触面处的临界问题.

解析对m1、m2的两个物体整体受力分析如图6，满足：F-f=(m1+m2)a

①

其中：f=μN=μ(m1+m2)g

②

③

对m1受力分析如图7：

F-f1-N21sinθ=m1a

④

其中：f1=μN1

⑤

N1+N21cosθ=m1g

⑥

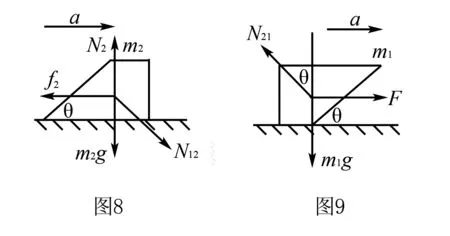
对m2受力分析如图8：N12sinθ-f2=m2a

⑦

其中：f2=μN2

⑧

N2=m2g+N12cosθ

⑨

由牛顿第三定律知：N12=N21

⑩

可知：当力F越大，N12越大,结合N1+N21cosθ=m1g可知：N1=m1g-N21cosθ越小.当N1=0时，也即f1=0.当力F再大一点，m1就会相对于m2滑动，满足不了题设条件，即m1、m2一起向右做匀加速直线运动被破坏.

于是m1受力分析图如图9所示：

满足：F-N21sinθ=m1a,N21cosθ=m1g

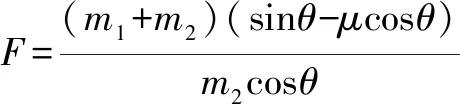
解后反思如例2这类试题，首先属于通过面接触的连接体问题，解题办法与前面方法相同.只不过当力F越大，m1就可能会相对于m2滑动，满足不了题设条件，抓住这个临界条件，即：m1受到地面的支持力N1=0，也即f1=0条件进行处理，即可解题.这需要我们同学认真体会，进而熟练处理这类问题.