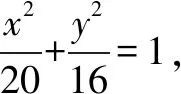圆锥曲线中的垂径定理

卢会玉

(甘肃省嘉峪关市第一中学 735100)

笔者发现高考中考查类似于圆的垂径定理的题目不时出现，值得深入探究.垂径定理是数学平面几何(圆)中的一个定理，它的通俗表达是：垂直于弦的直径平分弦且平分这条弦所对的两条弧.垂径定理是圆的重要性质之一，它是证明圆内线段、角相等、垂直关系的重要依据，也为圆中的计算、证明和作图提供了依据、思路和方法.如果能将圆的垂径定理所涉及的思想和方法迁移到椭圆、双曲线、抛物线上，那无疑是一种创新的研究思路.

一、试题呈现

题1 已知某椭圆的焦点是F1(-4,0),F2(4,0)，过点F2并垂直于x轴的直线与椭圆的一个交点为B，且|F1B|+|F2B|=10.椭圆上不同的两点A(x1,y1),C(x2,y2)满足条件：|F2A|,|F2B|,|F2C|成等差数列.

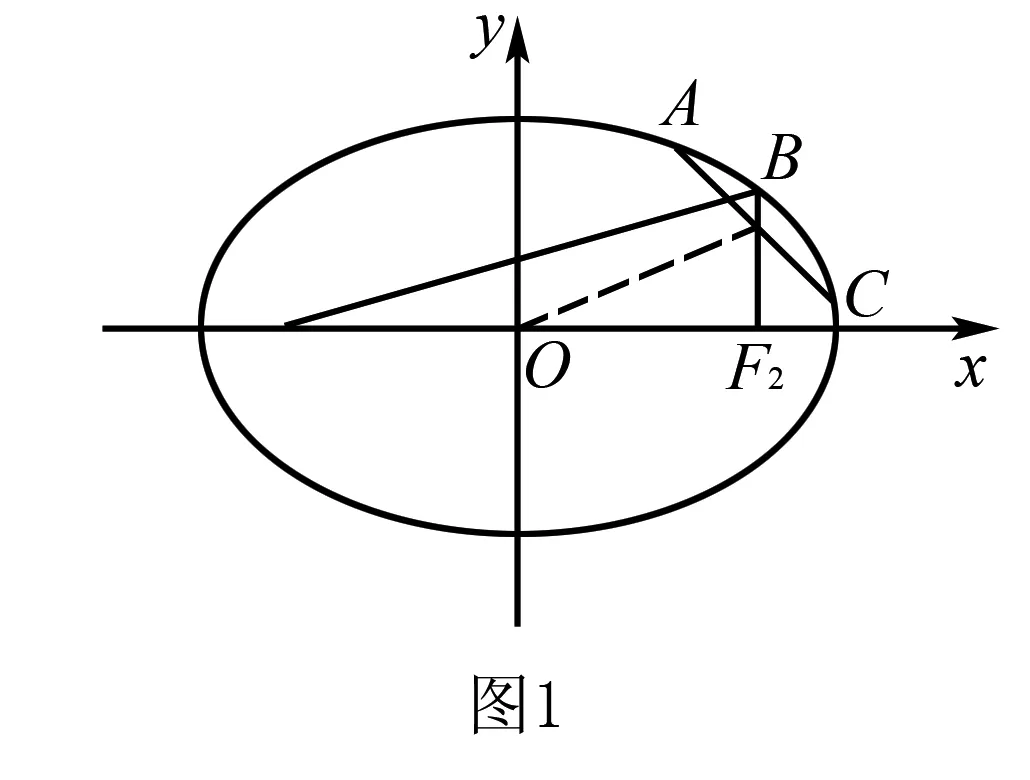
(1) 求该椭圆的方程；

(2) 求弦AC中点的横坐标；

(3) 设弦AC的垂直平分线的方程为y=kx+m，求m的取值范围.

二、试题解析

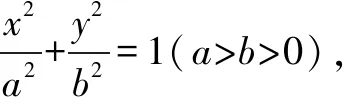
故弦AC中点的横坐标为4.

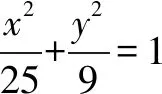
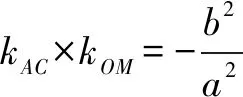
三、引申探究

1.圆中的垂径定理

为了讨论方便，假设下文所有问题的讨论中所涉及的直线的斜率都存在.

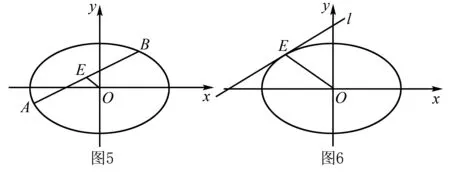
(1)如图2，在圆O中，E为弦AB中点，则OE⊥AB，即kOE·kAB=-1.那么，把弦AB向外平移到与圆相切，又会有什么性质呢？

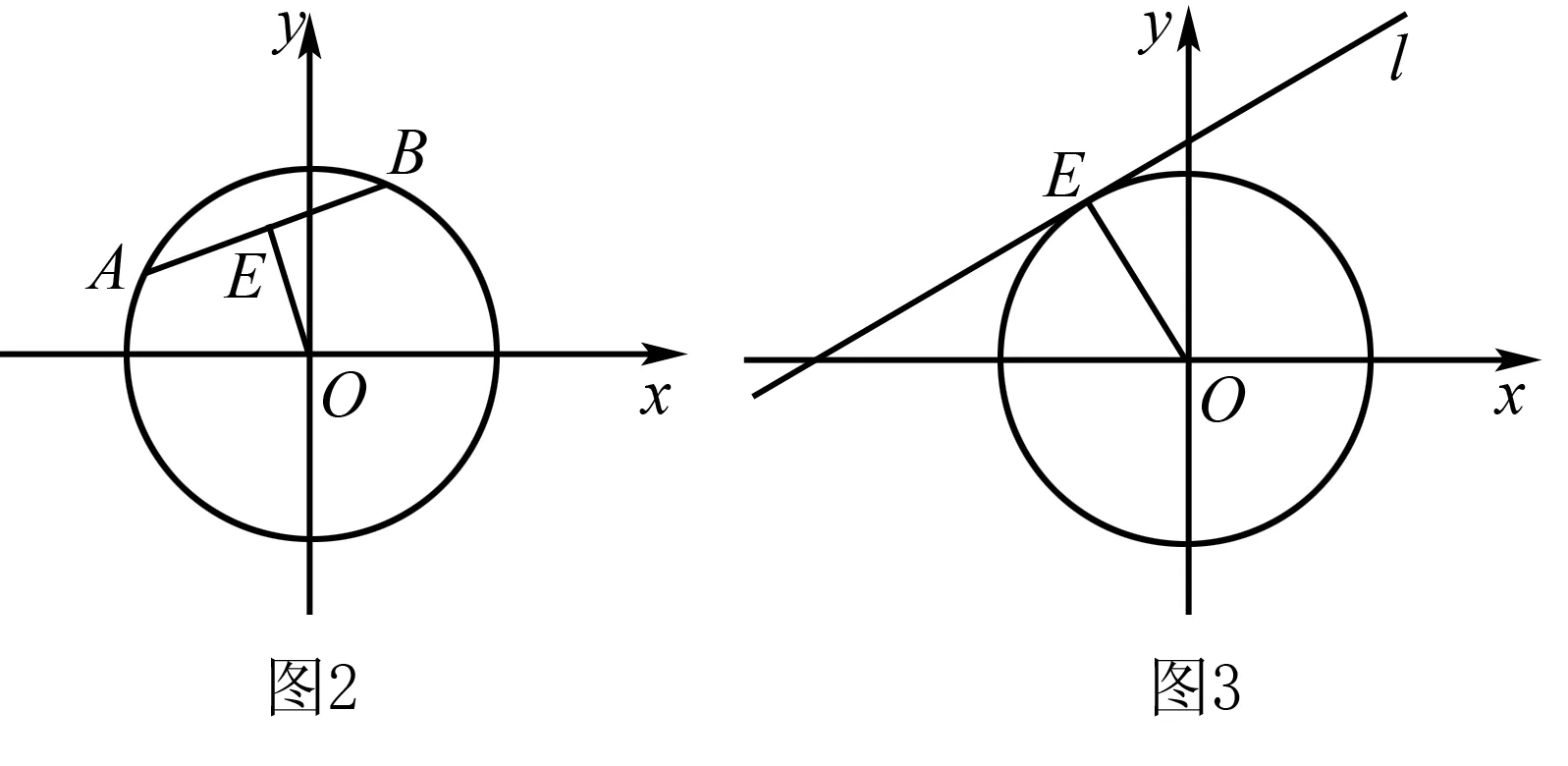
(2)如图3，在圆O中，直线l与圆O相切于点E，则OE⊥l，即kOE·kl=-1.那么，当弦AB过原点时，又会有什么性质呢？

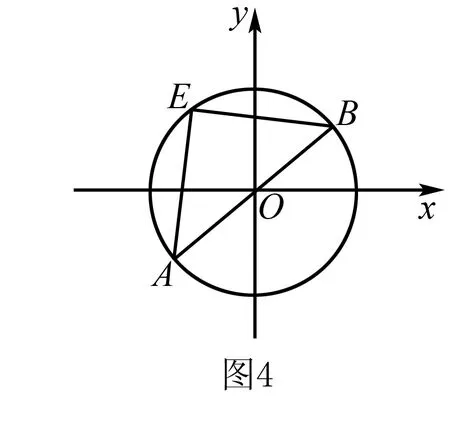
(3)如图4，AB为圆O直径，点E是圆上异于A，B两点的动点，则BE⊥AE，即kAE·kBE=-1.

2.椭圆中的垂径定理

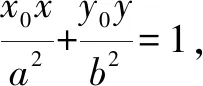
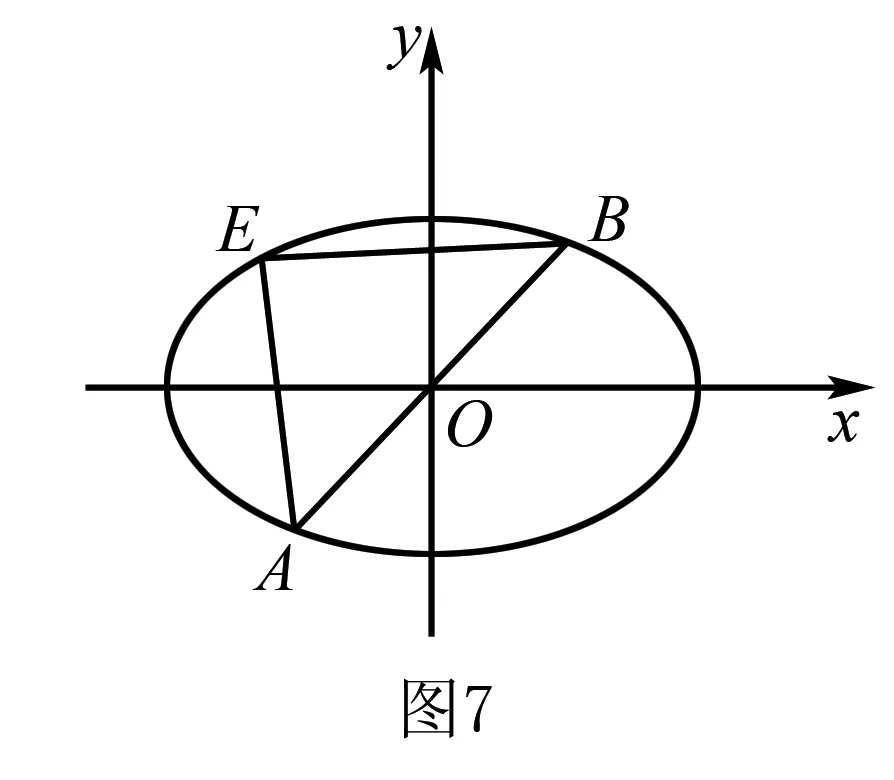
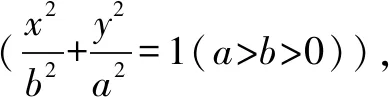
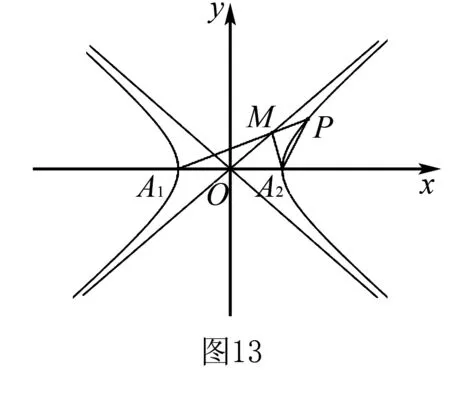
3.双曲线中的垂径定理

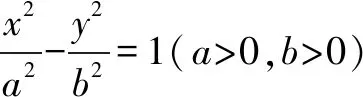
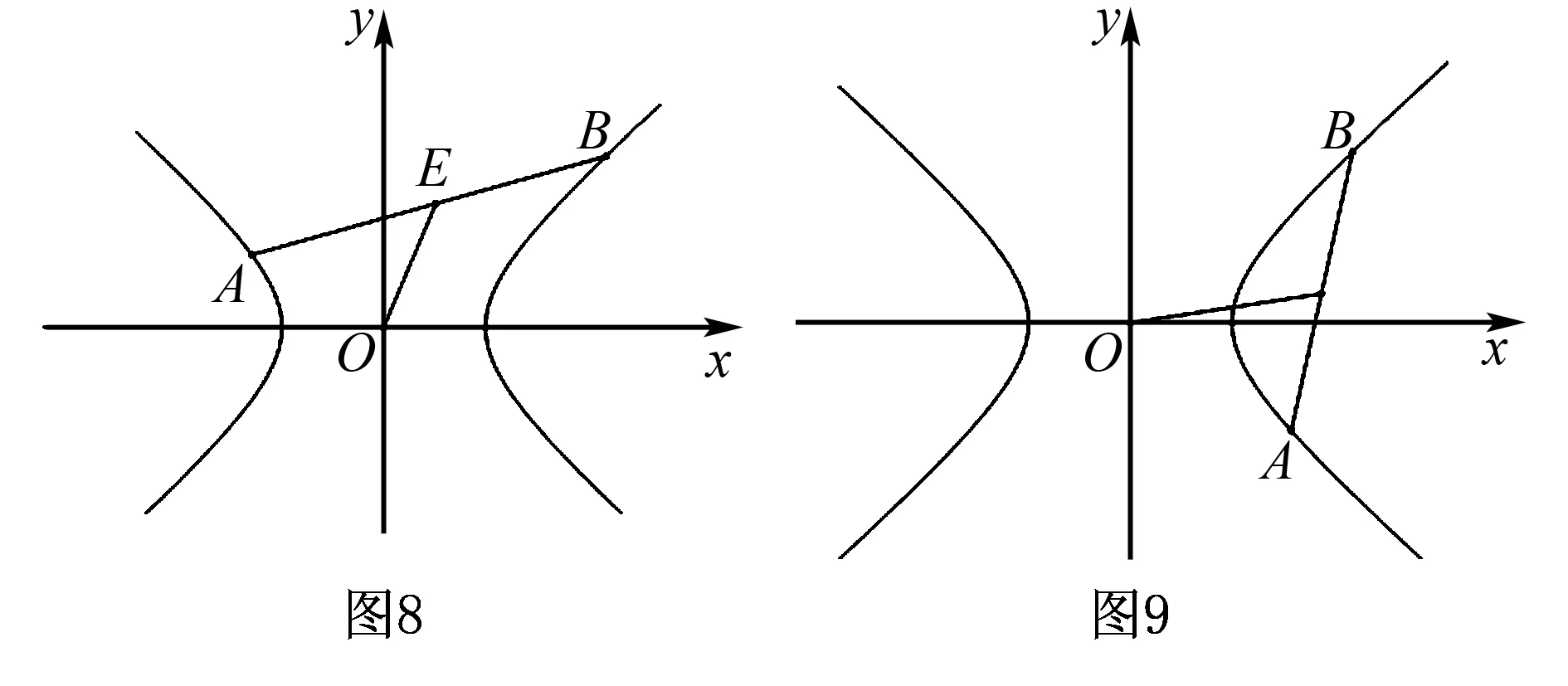
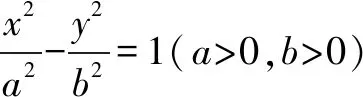
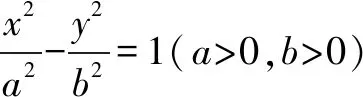
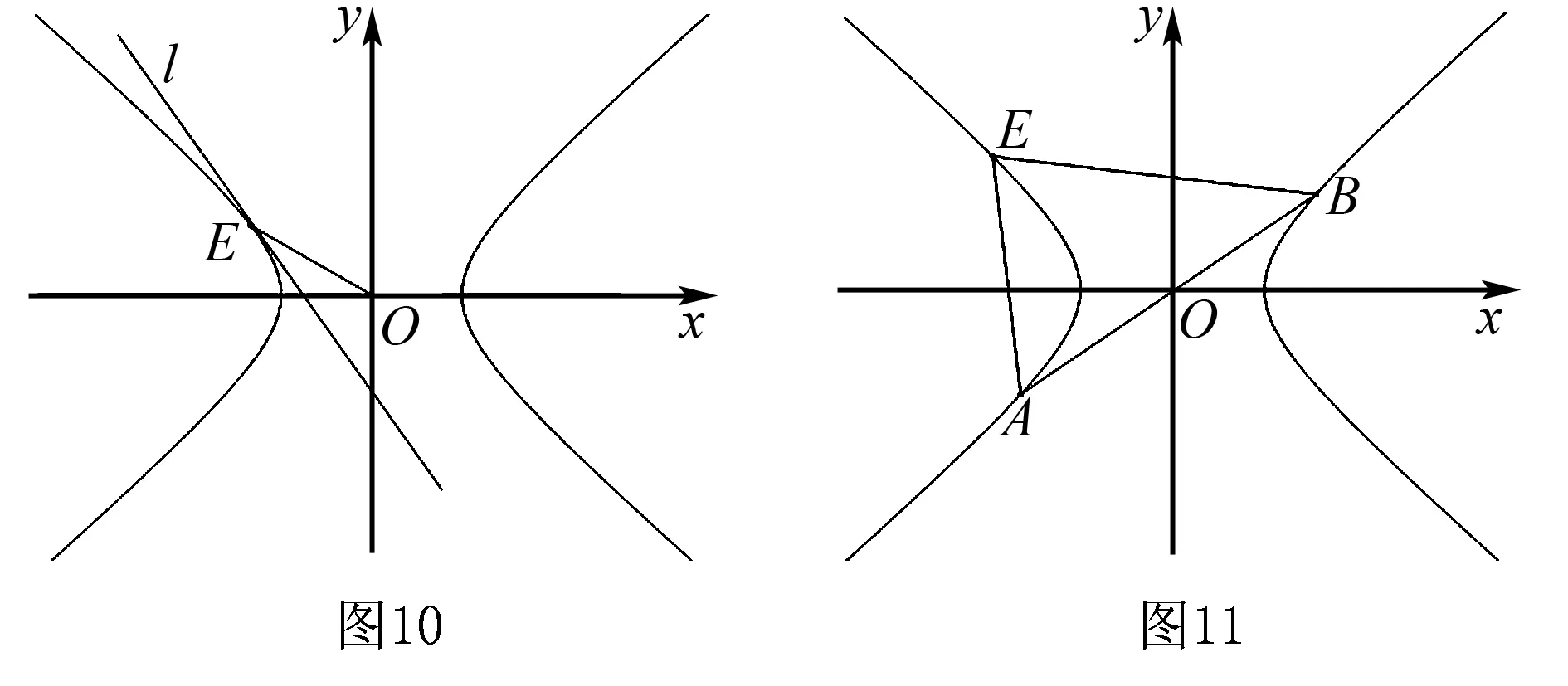
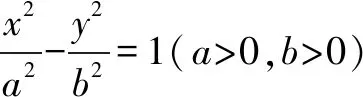
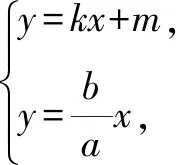
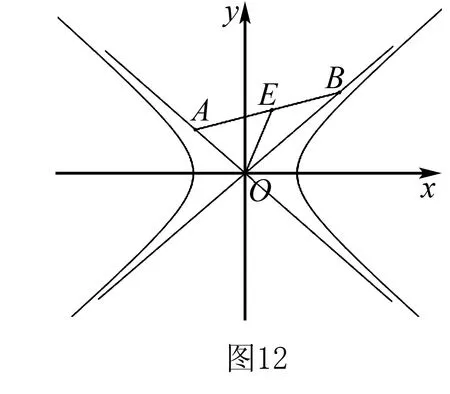
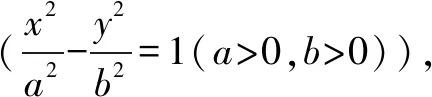
赵三喃喃着走出家门，虽然全村的人死了不少，虽然庄稼在那里衰败，镰刀他却总想出卖，镰刀放在家里永久刺着他的心。

4.圆、椭圆与双曲线(统称为有心圆锥曲线)中垂径定理的统一结论

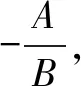
5.抛物线中的垂径定理

性质8 在抛物线y2=2ax(a≠0)中，E(x0,y0)为弦AB的中点，则kAB·y0=a.

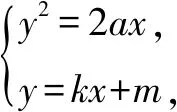
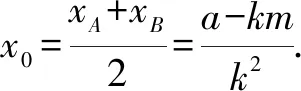
性质9 若直线l与抛物线y2=2ax(a≠0)相切于点E(x0,y0)，则kAB·y0=a.

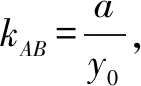
6.垂径定理的应用

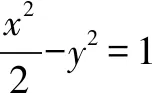
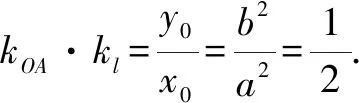
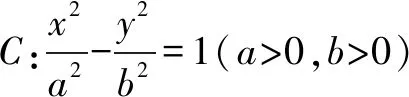
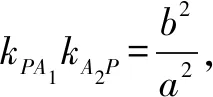
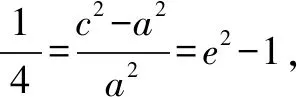
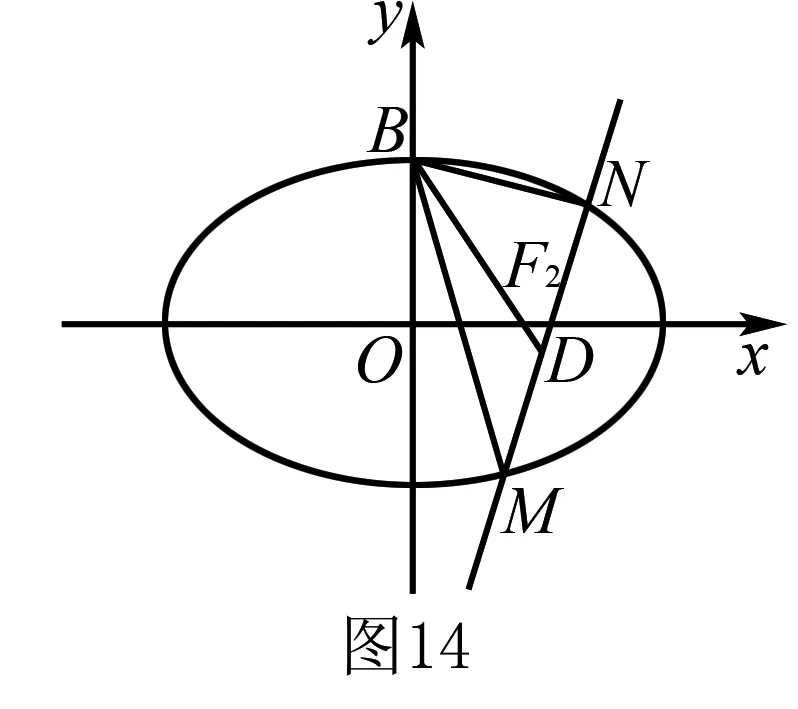
例3 已知直线l交椭圆4x2+5y2=80于M，N两点，B是椭圆与y轴正半轴的交点，若△BMN的重心恰好为椭圆的右焦点，则直线l的方程为____.