2020年高考全国Ⅲ卷理科第20题的解答与拓展

林国红

(广东省佛山市乐从中学 528315)

一、题目呈现

(1)求C的方程；

(2)若点P在C上，点Q在直线x=6上，且|BP|=|BQ|,BP⊥BQ，求△APQ的面积.

由于问题(1)较为简单，本文不作讨论，下面对问题(2)进行解答与探究拓展.

二、解法探究

分析由已知可得点B是定点，可考虑设P(x0,y0)，Q(6,n)，通过参数将题目的条件进行翻译与转化.

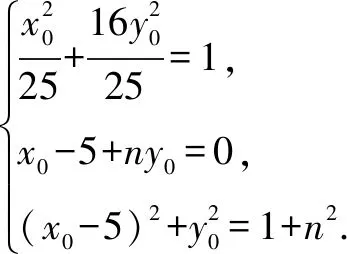
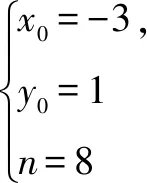
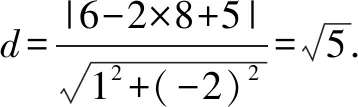
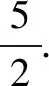
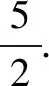
分析由题意，点P由直线BP与椭圆C确定，点Q由直线BQ与直线x=6确定，结合已知条件，利用直线BP的斜率k作为参数将题目的条件进行翻译与转化.

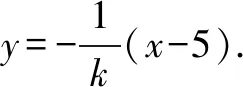
整理,得(1+16k2)x2-160k2x+(400k2-25)=0.

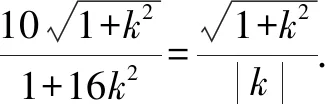
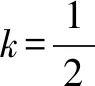
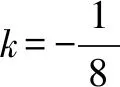
以下同解法1.

分析由条件|BP|=|BQ|，BP⊥BQ，可知由点P的坐标可以确定点Q的坐标，反之亦然.由于点Q的横坐标为6，故可用点Q的坐标来确定点P的坐标.仍然用斜率作为参数将题目的条件进行翻译与转化.

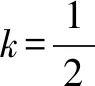
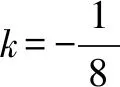
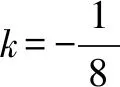
以下同解法1.

分析由椭圆的对称性，不妨设点P,Q在x轴上方.如图1，过点P作x轴垂线，垂足为点M，设x=6与x轴交于点N，由△PMB≌△BNQ，可求得点P坐标以及直线AQ的方程，根据点到直线距离公式和两点间的距离公式，即可求得C的面积.

解法4(平面几何角度)由椭圆的对称性，不妨设点P,Q在x轴上方.因为点P在C上，点Q在直线x=6上，且|BP|=|BQ|，BP⊥BQ，过点P作x轴垂线，垂足为点M，设x=6与x轴交于点N，如图1.

由于|BP|=|BQ|，BP⊥BQ，∠PMB=∠QNB=90°，又因∠PBM+∠QBN=90°，∠BQN+∠QBN=90°，故∠PBM=∠BQN，所以△PMB≌△BNQ.

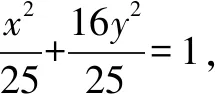
所以|PM|=|BN|=6-5=1.

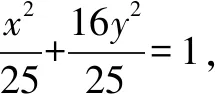
①当点P为(3,1)时，故|MB|=5-3=2.

因为△PMB≌△BNQ，所以|MB|=|NQ|=2，可得点Q为(6,2)，如图2.

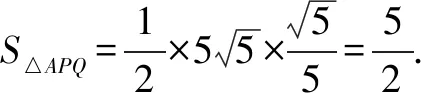
②当点P为(-3，1)时，故|MB|=5+3=8.因为△PMB≌△BNQ，所以|MB|=|NQ|=8,可得点Q为(6，8)，如图3.

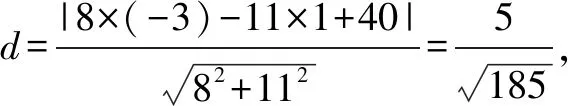
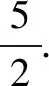
三、试题推广

将考题一般化，可以得到如下结论：

证明由椭圆的对称性，不妨设点P,Q在x轴上方,设P(xP,yP)，Q(k,yQ).因为点P在C上，点Q在直线x=k上，且|BP|=t|BQ|，BP⊥BQ，过点P作x轴垂线，垂足为点M，设x=k与x轴交于点N，如图4.

由于|BP|=|BQ|，BP⊥BQ，∠PMB=∠QNB=90°，又因为∠PBM+∠QBN=90°，∠BQN+∠QBN=90°，故∠PBM=∠BQN，所以△PMB∽△BNQ.

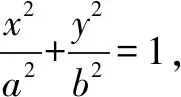
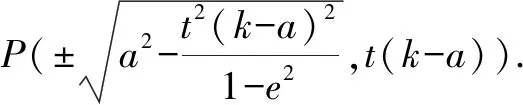
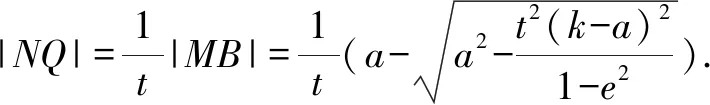
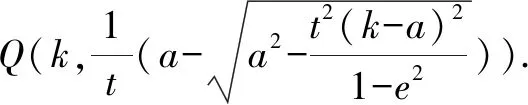
整理,得yQx-(k+a)y+yQa=0，

即yQ(x+a)-(k+a)y=0.

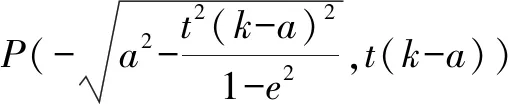
四、类比拓展

经探究，在双曲线中也有类似的结论：

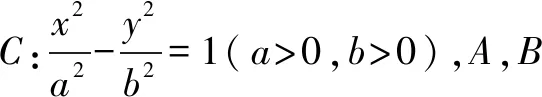
学数学离不开解题，对于一道优秀的试题，应该在获得解答的基础上，多角度展开尝试与联想，借助题目，探索隐藏在题目背后的奥秘，力求扩大战果.从特殊到一般的数学思想是解析几何中数学发现的重要手段，只有养成多思善想、举一反三，钻研到底的学习习惯，才能在学习中获得无穷的乐趣，使思维得到发展.