竖直面内杆连小球做圆周运动的杆中弹力方向分析*

谢禄桥 张轶炳

(宁夏大学物理与电子电气工程学院 宁夏 银川 750021)

圆周运动一节是选择性必修2第一章曲线运动中的重要内容，其杆模型下杆中弹力方向分析一直是教学的难点.学生在学习了竖直面内绳连小球做圆周运动的绳中弹力方向后，很容易类推得出杆模型下杆中弹力方向也沿杆的结论.显而易见，这种类推过渡方法极不严谨与准确.为了更好地利于一线物理教师教学及物理拔尖生的学习，以下将以杆连小球在竖直面内做圆周运动为例，将杆分为轻质杆与普通杆，进行杆中弹力方向分析的推理论证，希望能带来些启示与参考.

1 问题引入——杆施加给小球的弹力的方向是否一定沿杆

如图1所示，一杆连接小球在竖直面内做圆周运动，杆长为L，质量为m1，小球可视为质点，其质量为m2.小球现从最高点a处静止释放，经过图中b位置时，杆与竖直方向的夹角为β.试问：

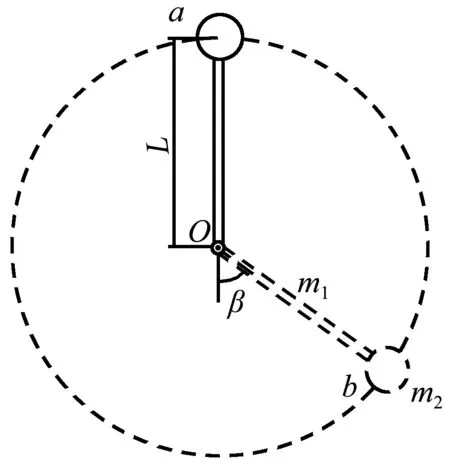
图1 杆连小球做圆周运动

(1)若杆为普通杆，则杆施加给小球的弹力方向是否沿杆，并给予证明；

(2)若将杆视为轻质杆，杆施加给小球的弹力方向是否沿杆，并给予证明.

1.1 普通杆施加给小球的弹力方向的推理论证

在第(1)问中，若杆为普通杆，即杆的质量不为零.现将杆与小球视为刚体，设杆的转动惯量为J1，小球的转动惯量为J2[1]，则

杆与小球作为整体并进行受力分析，如图2所示，则绕O点转动过程中的合力矩为

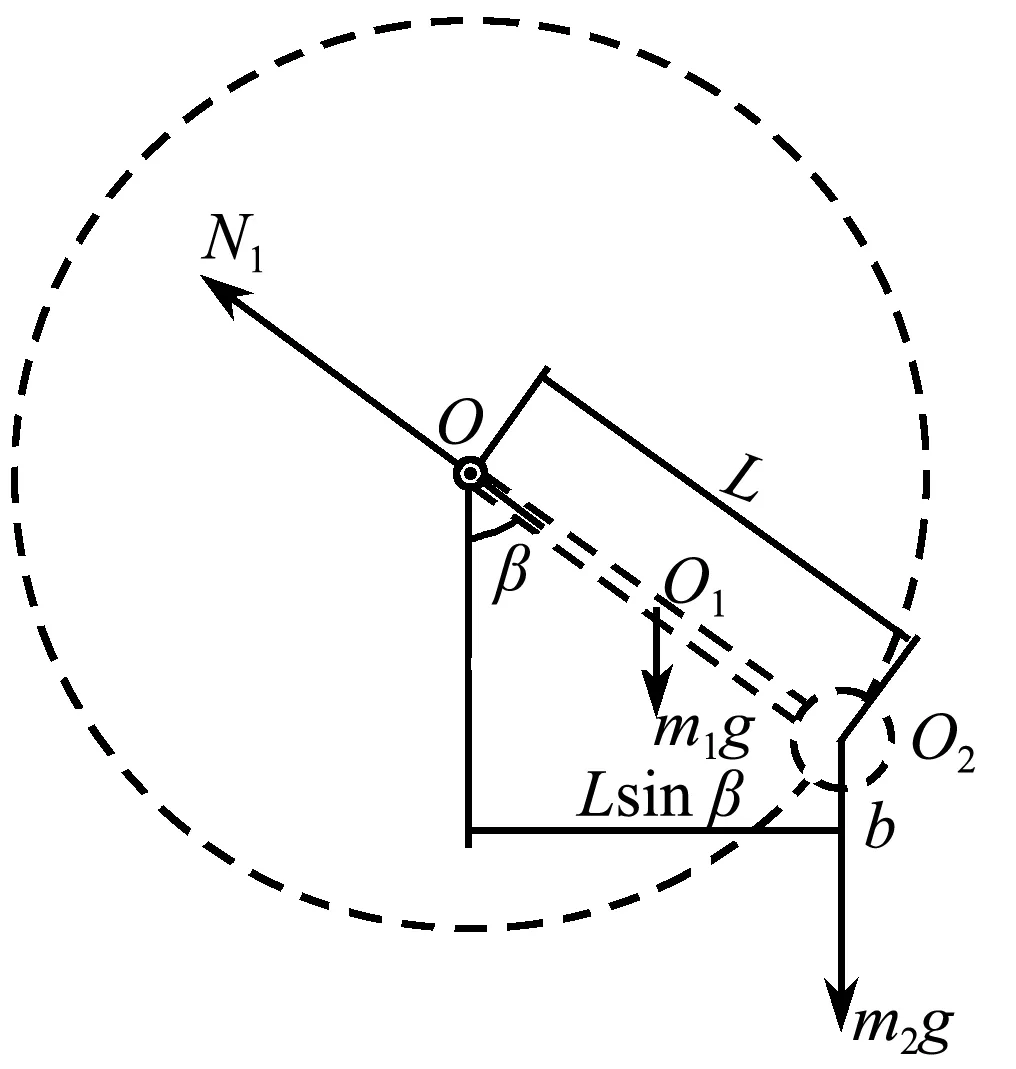
图2 整体受力分析示意图

根据力矩、转动惯量、角加速度间关系

M=(J1+J2)α

可得杆与小球整体的角加速度为

根据切向加速度与角加速度的关系

aτ=Lα

可得杆与小球整体的切向加速度为

(1)

现隔离小球，并假设杆施加给小球的弹力的方向沿杆收缩方向，如图3所示，分解重力得小球的切向加速度为

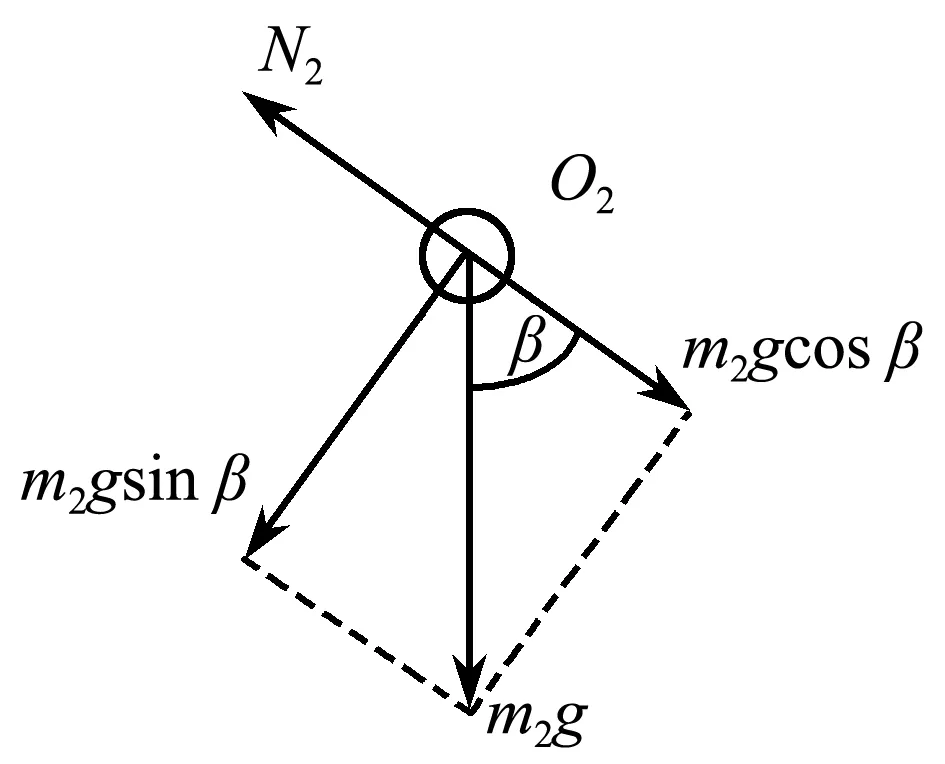
图3 小球受力分析示意图

a′τ=gsinβ

(2)

比较式(1)与(2)得

当β=0或π时，sinβ=0

ατ=α′τ

所以假设成立，即在最高点与最低点时，杆施加给小球的弹力的方向沿杆.

当β≠0或π时，sinβ≠0

ατ≠α′τ

所以，假设不成立，即在此过程中，杆施加给小球的弹力的方向不沿杆，且

即

ατ>α′τ

故小球从最高点向最低点运动过程中，杆给小球弹力不沿杆方向，与小球运动方向呈锐角，对小球做正功；当小球从最低点运动到最高点过程中，杆给小球弹力方向与运动方向呈钝角，对小球做负功.

综上可得，普通杆连接小球在竖直面内做圆周运动时，除最高点、最低点外，杆给小球弹力方向不沿杆，杆施加给小球的弹力要做功.即普通杆连接小球在竖直面内做圆周运动时，杆施加给小球的弹力的方向不一定沿杆.

1.2 轻质杆施加给小球的弹力方向的推理论证

在第(2)问中若将杆视为轻质杆，则杆的质量视为0，现对小球进行受力分析，如图4所示，证明如下：

小球的转动惯量为

J2=m2L2

杆与小球绕O点转动的力矩为

M2=m2gLsinβ

根据力矩、转动惯量、角加速度间关系

M2=J2α

可得杆与小球整体的角加速度为

由切向加速度与角加速度间关系

aτ=Lα

可得杆与小球整体的切向加速度为

aτ=gsinβ

(3)

现隔离小球，对其受力分析如图5所示，并假设杆施加给小球的弹力的方向沿杆，分解重力易得小球的切向加速度

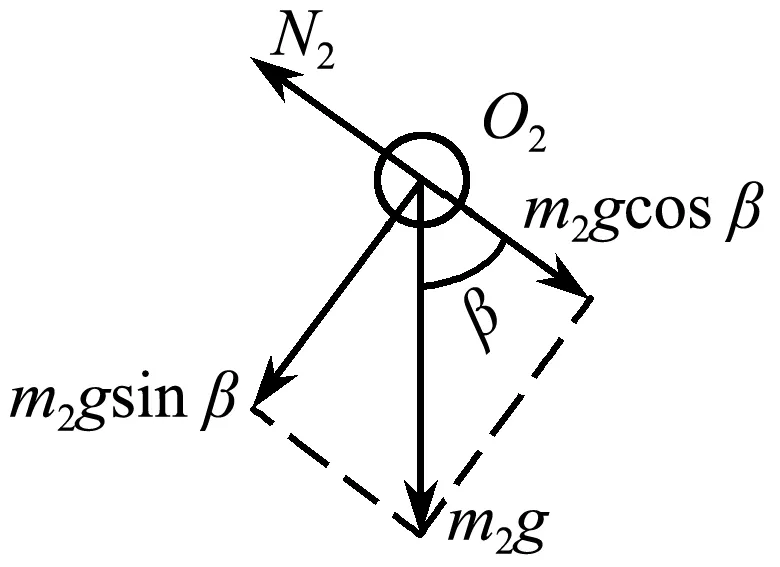
图5 小球受力分析示意图

a′τ=gsinβ

(4)

由式(3)与(4)可得，无论β为何值，总有

aτ=a′τ

所以，假设成立.即在图1模型中，若将杆视为轻质杆，整个过程中杆施加给小球的弹力的方向始终沿杆方向[2].

1.3 杆施加给小球的弹力方向的结论

在图1所示的模型中，我们将杆分为普通杆与轻质杆，并借助整体法、隔离法、假设法及讨论法，对杆施加给小球弹力的方向是否沿杆进行了推理论证，得出了如下结论：(1)普通杆连小球在竖直面内做完整圆周运动时，杆施加给小球的弹力的方向除最高、最低点外，一定不沿杆方向；(2)轻质杆连小球在竖直面内做完整圆周运动时，杆施加给小球的弹力的方向一定沿杆方向.

2 问题升华——轻质杆施加给小球的弹力方向是否一定沿杆

由以上图1模型及证明可知，普通杆施加给小球的弹力的方向不一定沿杆，那轻质杆施加给小球的弹力方向一定沿杆吗？我们以图6模型为例进行推理论证.

如图6所示，一轻质杆连接两小球在竖直面内做完整圆周运动，杆中点处小球编号为1，质量为m1，杆最外端小球编号为2，质量为m2；杆长为L，杆可绕O点自由转动；小球的半径相对于杆长较小，可将小球视为质点.现将小球从图中a位置顺时针轻轻扰动下，当杆与小球经过图中b位置时，此时杆与竖直轴线间夹角为β.试问：轻质杆施加给小球的弹力方向一定沿杆方向吗？并给予证明.

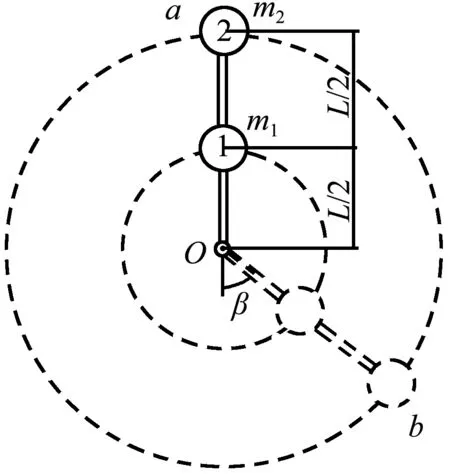
图6 轻质杆连两小球做圆周运动

2.1 轻质杆施加给小球的弹力方向的推理论证

将两小球视为刚体，设小球1的转动惯量为J1，小球2的转动惯量为J2，则

现将两小球及轻质杆视为一个整体，如图7所示，对O点取力矩，则

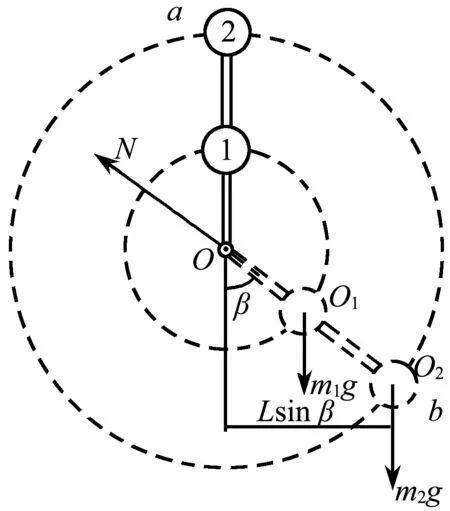
图7 整体受力分析示意图

整体的转动惯量为

J=J1+J2

根据力矩、转动惯量、角加速度间关系

M=Jα

可知两小球及轻质杆整体的角加速度为

由切向加速度与角加速度间关系

aτ=Rα

可得，在b位置时，小球2的切向加速度为

(5)

小球1的切向加速度为

(6)

现分别隔离m2和m1，并假设杆施加给小球的弹力方向均沿杆，如图8所示，分解重力易得两小球的切向加速度为

a′τ2=a′τ1=gsinβ

(7)

(a)球2受力示意图 (b)球1受力示意图

对比式(5)、(6)、(7)可知，当β=0或π时

aτ1=a′τ1=aτ2=a′τ2=0

故假设成立，即在最高点、最低点时，杆施加给两小球的弹力方向均沿杆方向.

对小球2分析，当β≠0或π时，由于

即

aτ2>a′τ2

故小球2从最高点向最低点运动过程中，杆给小球2弹力不沿杆方向，与小球2运动方向呈锐角，对小球2做正功；当小球2从最低点运动到最高点过程中，杆给小球2弹力方向与运动方向呈钝角，对小球2做负功.

对小球1分析，由于

即

aτ1

故小球1从最高点向最低点运动过程中，杆给小球1弹力不沿杆方向，与小球1运动方向呈钝角，对小球1做负功；当小球1从最低点运动到最高点过程中，杆给小球1弹力方向与运动方向呈锐角，对小球1做正功.

综上可知，在图6所示的模型中，除最高点、最低点外，轻质杆施加给两小球的弹力方向均不沿杆.即整个过程中，轻质杆对两小球的弹力方向不一定沿杆.

3 结论与建议

通过对杆连小球在竖直面内的圆周运动的杆中弹力方向分析的推理论证，我们意识到，在竖直面内的圆周运动的动力学问题中，轻质杆与普通杆对连接体的弹力方向都不一定沿杆.当组成系统的两个物体之间有机械能相互传递时，通过杆中弹力做功实现这种机械能的传递，故杆中弹力方向不沿杆；当组成系统的这两个物体的角速度有最大值或最小值时，杆的弹力方向才沿杆或为零.

因此，物理一线教师在进行杆模型在竖直面内做圆周运动的教学时，应根据具体情况具体分析，合理设置物理情景，让学生理解性地掌握杆中弹力方向的特点.如教师在讲解绳、杆连接一小球在竖直面内做圆周运动一节知识时，如何能有效地让学生从绳模型顺利地过渡到杆模型，并理解轻质杆施加给该小球的弹力的方向时刻沿杆方向，往往成为该堂课教学成败的关键.再如教师在讲解轻质杆连两小球在竖直面做圆周运动系统机械能守恒时，如何让学生理解“除最高、最低点外，杆施加给两小球的弹力方向不沿杆，单个小球机械能不守恒，但系统的机械能守恒.”这部分核心知识也成为该节课成败的关键.所以，一线教师在进行物理学科教学及针对物理拔尖生的培养时，应进行专门辅导、适度拓展，注意引导学生理解性掌握，忌机械灌输，只重视知识的熟记；教师应立足学生长远发展，重视论证、探究方法的掌握，培养学生的物理学科核心素养，多为国家输送基础学科的优秀拔尖人才.