基于极简教育技术理念的点电荷镜像法电场可视化研究*——以GeoGebra软件为例
2021-11-23周志毅丁益民李子健
向 倩 周志毅 丁益民 李 政 李子健
(湖北大学物理与电子科学学院 湖北 武汉 430062)
为了聚焦新时代对人才培养的新需求,将教育信息化作为教育系统性变革的内生变量,支撑引领教育现代化发展,推动教育理念更新、模式变革、体系重构,教育部制定了《教育信息化2.0行动计划》[1].作为高等学校一线教师,如何充分把握好这一机遇,落实教育部的这一要求,实现教育信息化2.0的宏伟目标呢?随着信息技术突飞猛进的发展,面对教育信息化浪潮,极简主义思路值得借鉴和运用.我们可以将极简主义理念和教育技术实践有机结合起来,以应用驱动为导向加快推进教育信息化,坚持深化应用,促进高等教育质量的提升[2].随着软硬件技术的长足发展及其在教育领域越来越广泛的运用,电脑及智能手机的大量普及为在教学上推广极简教育技术提供了硬件支持;网络上涌现出一大批优秀教学应用软件给学校师生运用极简教育技术提供了极为丰富的资源选择.以优秀的数学模拟软件GeoGebra为例,借助这个软件,师生能够很方便地学习、研究点电荷电场的电势和电场的分布特点.
模拟软件GeoGebra是奥地利数学家Markus Hohenwarter开发的一款超越几何画板态势的动态数学软件[3],其优点在于几乎无需编程基础,简单易学,操作简便,使用起来快捷高效[4].该软件在网络上可以免费下载,通过使用函数和变量定义能精确地绘制复杂图形,并能方便地实现几何图形的动态变化演示,将本软件用于物理教学十分符合极简教育技术理念的要求与特点.
镜像法求静电场是电动力学中的一个重要的教学内容,然而由于电场的空间分布都十分的复杂和极具抽象性,并且需要较深的数学理论知识,使得学生在学习时困难重重,也容易丧失学习的兴趣,因此静电场的可视化在教学中具有重要意义[5~7].为了解决这个问题,本文利用GeoGebra的3D绘图功能实现点电荷的3种镜像电场可视化为例,解决镜像法求解电场中电势分布、等势线的细节描述的难点,实现抽象的理论知识转化为直观形象的动态演示,为大学物理教师提供基于极简教育技术的教学思路及理念.
1 点电荷与无限大接地导体平面的电场
设无限大导体平面位于xOz面内(如图1阴影区域),其右侧距平面h处有一点电荷Q1,带电荷量为q.为了计算上的简化及数学形式上的对称性,将Q1置于y轴.由镜像法可知镜像电荷Q2带电荷量为-q,位置与Q1关于导体对称,因此也位于y轴,且到xOz面的距离为h′=h.点电荷与无限大接地导体平面(即xOz面)的镜像电荷和位置如图1所示.

图1 点电荷与无限大接地导体平面的镜像电荷和位置
在空间直角坐标系中,点电荷Q1(x1,y1,0),镜像电荷Q2(x2,y2,0),由于在三维空间无法描绘出4个变量之间的关系,且点电荷与镜像电荷的场分布具有轴对称性,因此只需要考虑平面xOy内任意点P(x,y, 0)的电势分布,其电势函数可表示为
(1)
由对称性可知,x2=x1,y2=-y1.
可视化实现:
(1)打开GeoGebra,选择【3D绘图区】,设置滑动条“q”“h”“k”.为了便于作图,取静电常数k=1,不影响电势分布的大致形状.然后确定电荷的位置,在输入区输入点电荷的位置“Q1=(0,h,0)”,镜像电荷位置“Q2=(0,-h,0)”.
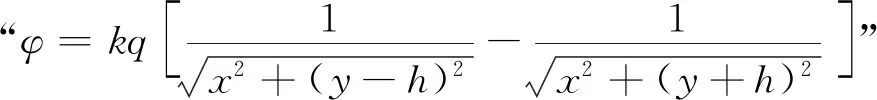
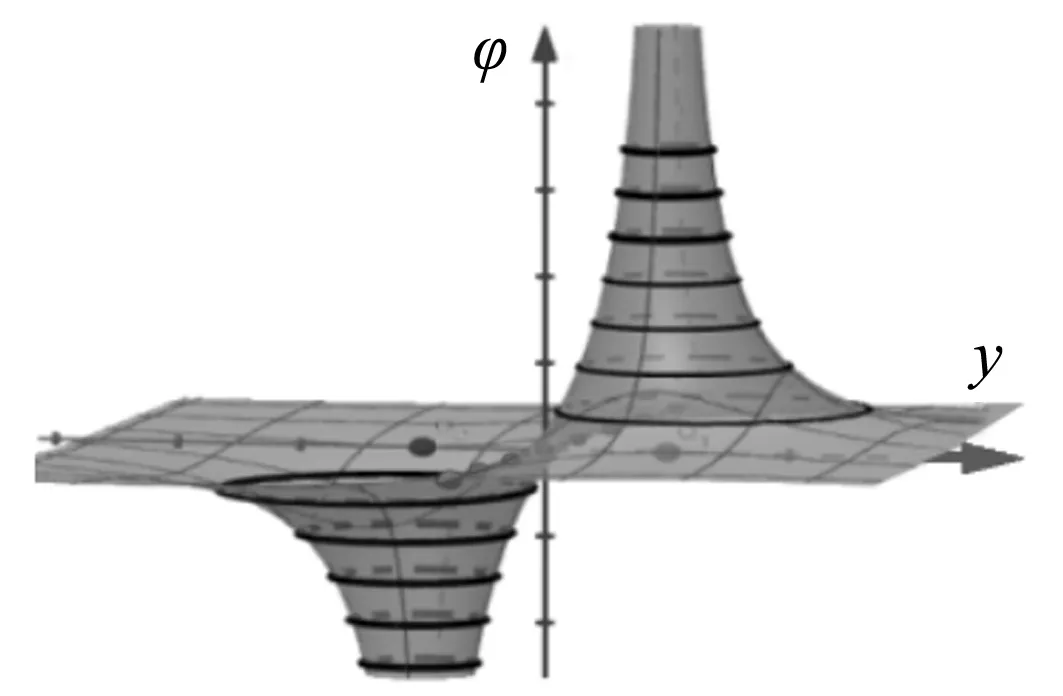
由函数φ(x,y)的性质不难推出,当x→0,y→h时φ(x,y)→+∞;当x→0,y→-h时φ(x,y)→-∞,因此在这两个点附近,电势曲面表现为朝上下两个方向上无限延伸的高高突起的尖柱形状.由于φ(x,y)=-φ(x,-y),函数呈中心对称,曲面上的点关于O点在xOz两侧面呈中心对称,因此这两个柱体位于xOz两侧朝反方向无限延伸(如图2),其中z轴表示电势,x,y表示空间位置坐标.图2中电势曲面上的纵坐标表示xOy平面内某点的电势数值,曲面上关于O对称的两点,其电势等值异号.

图2 电势的空间分布
(3)在输入区输入“x=0”,就会出现一个新的平面,即yOz平面,在工具栏点击【相交曲线】工具后点击两个面即得到平面x=0与电势分布曲面的交线(如图3).接着隐藏两个面,移动鼠标的同时按住鼠标右键可从不同视角方向观察三维电势分布的截面图.下面图3呈现的是电势分布曲面φ(x,y)为x=0平面所截后电势在yOz平面上的分布曲线.

图3 点电荷与镜像电荷在yOz面的电势分布
(4)在输入区分别输入“z=0.2”“z=0.5”“z=1”“z=2”“z=4”“z=7”“z=-0.2”“z=-0.5”“z=-1”“z=-2”“z=-4”“z=-7”,这几个面相当于等势面,通过【相交曲线】工具,得到以上几个面与电势分布曲面的交线,即得到等势线的空间分布图4(a),隐藏各个面,俯视得到点电荷与镜像电荷等势线的二维平面图,如图4(b).
(a)等势线空间分布
2 点电荷与接地导体球面的电场
半径为a的接地导体球外有一个点电荷q,点电荷距离球心为d,点电荷与接地导体球面的镜像电荷q′ 的大小和位置如图5所示.

图5 点电荷与接地导体球面的镜像电荷的大小和位置
根据镜像法,镜像电荷量
(2)
镜像电荷的位置
(3)
设P点位于xOy平面上,坐标为(x,y,0),电势函数表示为
(4)
其中
(5)
(6)
(7)
(8)
可视化实现:
(1)设置滑动条“q”“a”“d”“k”“θ”.依旧令k=1,且d>a.在输入区依次输入式(2)和(3),“Q1=(d,0,0)”和“Q2=(d′,0,0)”.
(2)由于电势函数较为复杂,依次在输入区输入式(5)、(6)、(7)、(8).
(3)在输入区输入电势函数(4),便可绘制出图6(a).
(4)同第一种镜像电场的操作方式,可绘制点电荷与镜像电荷连线方向的电势分布如图6(b),等势线空间分布如图6(c),等势线二维平面分布如图6(d).

(a)电势空间分布
3 点电荷与不接地导体球面的电场
当导体球不接地时,此时除了有镜像电荷q′外,还存在另一个位于球心的镜像电荷q″,使得导体球总体带电量为零.点电荷与不接地导体球面的镜像电荷的大小和位置如图7所示.

图7 点电荷与不接地导体球面的镜像电荷的大小和位置
根据镜像法
q″=-q′
(9)
d″=0
(10)
此时P点的电势函数表示为
(11)
可视化实现与以上两种情景类似,本部分不再详述,最后通过GeoGebra分别绘制如图8所示.
移动滑动条上各变量,会发现各图像形成动态变化,即电势大小随着各个变量的改变而改变,但是电势大致的分布没有受到影响.显然以上图像显示的结果与传统教学过程中得到的结论是一致的.而且这些图形是根据数值计算结果绘制出的,比目前众多教材中还在大量采用的示意性图准确可靠.

(a)电势空间分布
5 结束语
本文旨在尝试在教学工作中运用极简教育技术推进课堂教学信息化,以极简主义理念所倡导的师生使用方便、直观、实用、易学、易用作为出发点,以GeoGebra软件对静电场中点电荷的3种镜像法电场进行可视化研究为例,生动鲜活、直观详尽地展现了在镜像电场中各个视角的电势分布和等势线分布情况.在以往的教学中,学生很难通过公式推导和课本上呈现的二维平面图,就能了解不同电场中电势分布情况,然而借助极简教育技术,利用GeoGebra开展静电场仿真教学,很容易地令点电荷镜像法电场可视化后,化抽象的概念为直观的认识,学生通过分析3D图像,会发现不同镜像电场的各个视角的电势分布图像各有特点,以及软件页面的颜色区分和动态效果,加深了学生对不同场分布结构的印象和理解,从而达到极简教育技术所倡导的目的,为广大教师推动教育观念更新、在教学中推进新技术支持下的教育教学创新思路提供参考与借鉴.
