寡头博弈模型中的时间记忆性质与预期对模型稳定性的影响

赵佳丽， 梁晏铭

(西安财经大学 统计学院， 西安 710100)

2021年中央经济工作会议、中央财经委员会第九次会议强化反垄断工作作出决策部署，将反垄断工作重要性提升到前所未有的高度。“十四五”规划建议明确提出健全公平竞争审查机制，加强反垄断和反不正当竞争执法司法，提升市场综合监管能力。强化反垄断，是党和国家作出的重大决策部署，加快构建更加安全、更加公平、更具活力、有效竞争的经济市场体系。基于此，研究垄断问题对于国家的经济发展具有重要现实意义。

寡头垄断市场是现实中较为普遍存在的市场结构，事实上，经济市场中存在很多寡头垄断现象，尤其是在那些需要在大规模的基础上才能实现经济效益的产品市场出现这种市场结构。这些企业为了利润最大化，不断地竞争，制定出最有利于自己的策略。而博弈论就是研究这种具有斗争或竞争的经济现象，各博弈方为了各自的目标和利益最大化，在研究优化策略时，要尽可能考虑对方可能采取的策略，以调整自身的策略。这种博弈行为在寡头垄断市场中表现得更为明显。

寡头垄断市场格局的普遍性使得对寡头垄断行为和市场博弈的研究更有实际意义，因此吸引了大量学者进行研究。对寡头模型的研究主要从产量和价格两种策略角度进行，学者们以此为基础，对市场经济竞争中寡头企业的行为进行研究，如垄断企业的数据信息博弈、粮食交易中的价格博弈等。

企业的发展与社会经济的发展息息相关，一荣俱荣。因此企业的发展要适应社会的发展进程，要善于利用社会条件发展自己，同时做出利于经济市场发展的决策，推动社会经济发展。寡头垄断现象较为普遍，像电力价格垄断、油价垄断，以及银行垄断、保险公司垄断，BAT这种大公司的对市场的垄断，对大数据信息的垄断，等等，这些垄断现象对国家安全健康发展有很大的影响，因此研究寡头垄断下的市场稳定性具有至关重要的现实意义。

1 研究综述

产量模型最早是由法国学者Cournot提出的，是最早的寡头模型，该模型是以调节产量为主的模型，因此叫产量模型，也叫古诺模型。价格模型是在产量模型的基础上建立的，它是以调节价格为主的模型。关于产量模型和价格模型的稳定点存在性和稳定性判断研究主要是基于纳什均衡的稳定性判别研究。

1950年，Nash在EquilibriumPointinN-personGames和Non-cooperativeGames两篇论文中，首次提出“纳什均衡(Nash equilibrium)”，证明了均衡解[1]的存在性，揭示了博弈论与经济均衡的内在联系,从此把它应用到产量模型。

产量模型作为纳什均衡应用的最早版本，在产量博弈中应用广泛，对于产量模型的稳定性研究，比如Okuguchi[2]进行的双寡头垄断研究，Huck等[3]通过实验模拟进行的实验性双寡头市场内生时机研究，他的研究是利用纳什均衡，给出了双寡头模型解(均衡点)的存在性证明及其平衡稳定性的分析，特别是对连续双寡头模型的非线性稳定性研究中证明了模型常数阶的稳定性。Agliari等[4]研究的具有差异化产品的古诺双寡头博弈的动态系统，采用梯度学习机制来调整市场上个产品销售的数量，也就是利用了市场的时间记忆来调节产量，分析了模型稳定和不稳定时的产量情况对利润的影响，得出了调整产品的产量结构时，产量结构越丰富，模型越不稳定。学者们还将双寡头模型的研究推广到了离散双寡头经济模型，并对其进行了时间的定性分析，得出了从离散模型到连续模型，恒定的稳态不变的结论。

随着中国市场经济社会市场结构的不断发展和进步，很多经济学家、学者也不断研究寡头模型，比如雷勇等[5]分析了寡头厂商的博弈情况，马军海等[6]分析了延迟决策对寡头博弈的影响，张雅慧[7]分析了半合作模式下两阶段双寡头博弈模型，并对其进行了复杂动力学分析，徐峰等[8]研究了双寡头广告博弈模型的影响因素，分析了广告投入与其带来的利润关系。这些学者们的研究都是对不同的寡头模型进行了均衡性分析，并从不同的角度对均衡点的存在给出理论证明，分析了均衡点的稳定状态，以及各模型参数下系统的均衡态趋势。

价格模型的研究是在产量模型的基础上进行的，它以调节价格为主，以价格作为竞争手段，是产量模型的一种推广。比如Bester[9]基于消费者偏好的横向差异化，研究了双寡头垄断中Bertrand价格竞争的稳定性，并对其稳定性进行了分析，发现存在价格博弈均衡。吴险[10]在Bertrand模型的基础上，在分析“伯特兰德悖论”的解决方法时，进一步说明了模型稳定性是可以达到的。胡玉凤、张晨义[11]同样基于Bertrand模型和产品差异化思想，建立定价博弈模型，对扩展的Bertrand模型进行研究，分析了竞争者数量和产品替代率对均衡价格的影响。综上所述，寡头博弈模型的稳定性影响因素复杂多样，并且在有限条件下是能够达到稳定状态的，通过对均衡点的求解，可以找到均衡点或均衡局域对模型的稳定性进行研究。

2 模型的建立

本文研究两个厂商的产量博弈，根据已有的文献，以企业自身的产量对自身的产品产量的影响作为一个因素，以竞争对手的产品产量对自身的产品产量的影响作为一个因素，建立产量模型。考虑到时间的记忆性会对决策产生影响，因此引入分数阶理论，研究时间记忆对寡头博弈过程中模型的稳定性产生的影响。模型建立在古诺假设的基础上，只考虑企业自身产量和竞争对手产量对产量的影响，且认为市场总容量保持不变，无政策及其他外界因素干扰。模型的影响因素主要有厂商i(i=1，2)的互相影响作用γ，厂商i(i=1，2)对自身产量的影响作用Li，厂商i(i=1，2)的最大产量θi，连续的时间尺度u和v，企业产量的调整速度a和ν，厂商i产品生产的连续时间状态α。

当厂商1生产的产品数量达到一定数额后将会出现利润下降，此时厂商i对自身的产量产生影响，设影响因数为Li，建立模型为

∏(u,v)=θ1-γv-L1u

(1)

∏(u,v)=θ2-γu-L2v

(2)

根据式(1)、式(2)得到关于u和v的非线性连续系统，即

(3)

(4)

对应的预期为

(5)

(6)

3 实证分析

下面通过具体的实例对系统进行分析，在不同的分数阶条件下，利用wolfram alpha求解模型的均衡点、模型的特征矩阵、特征根以及特征根的幅角，分析均衡点的稳定性，判断系统的稳定性。首先介绍阶数为1时系统均衡点的稳定性分析方法，为后面分数阶系统的分析做理论铺垫。

3.1 阶数为1时的分析

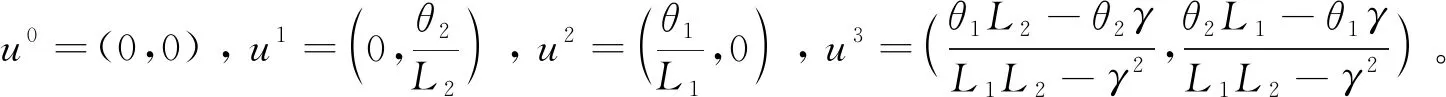
对式(3)关于u、v分别求偏导得

(7)

(8)

线性化得

(aθ1-aγv-2aL1u)u-aγuv

(9)

对式(4)关于u、v分别求偏导得

(10)

(11)

线性化得

-νvγu+(νθ2-νγu-2νL2v)v

(12)

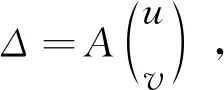
当所有的特征值λ的实部小于0时，系统的均衡点稳定，特征值λ的实部大于0时，系统的均衡点非稳定。

根据已有的文献，设θ1=0.5，θ2=1，γ=1，L1=3，L2=2，a=1.5，ν=2.5，此时的产量模型为

∏(u,v)=0.5-v-3u

(13)

∏(u,v)=1-u-v

(14)

由上面的分析知，α=1时，关于u和v的非线性连续系统为

(15)

(16)

在满足预期时，解得模型的均衡点为(0,0),(0,0.5),(0.167,0)。

在(0，0)处，特征值为0.75和2.5，系统是不稳定的；在(0，0.5)处，特征值为0和-2.5，系统是不稳定的；在(0.167，0)处，特征值为-0.75和2.08，系统是不稳定的。

此结果说明，当阶数为1时，系统易受外界因素的干扰，即厂商i(i=1，2)的产量易受到其竞争对手产量的影响，也容易受到自己上一期产量的影响。

3.2 阶数小于1时的分析

与阶数为1时的分析过程相同。

当α=0.2时：在(0，0)处，特征值为-0.5和3.75，此时系统是不稳定的；在(0，0.5)处，特征值为0和3.75，此时系统是不稳定的；在(0.167，0)处特征值为3.555和-1.055，此时系统是不稳定的。

当α=0.5时：在(0，0)处，特征值为2.5和0.75，此时系统是不稳定的；在(0，0.5)处，特征值为0和0.75，系统是不稳定的；在(0.167，0)处特征值为0和2.5，此时系统是不稳定的。

当α=0.8时：在(0，0)处，特征值为-0.59-0.59i，-0.59+0.59i，-1.39i，1.39i和0.59-0.59i，此时系统是不稳定的；在(0，0.5)处，特征值-0.47-0.47i，-0.47+0.47i，-1.47i，1.47i，和0.47-0.47i，此时系统是不稳定的；在(0.167，0)处特征值为-0.72-0.72i，-0.72+0.72i，-1.37i，1.37i和0.72-0.72i，此时系统是不稳定的。

3.3 阶数大于1时的分析

当α=1.5时：在(0，0)处，特征值为-0.78-1.35i，-0.78+1.35i，0.39-0.69i，0.39+0.69i，此时系统是不稳定的；在(0，0.5)处，特征值为-0.84-1.45i，-0.84+1.45i，0.29+0.51i和0.29-0.51i，此时系统是不稳定的；在(0.167，0)处特征值为-0.76-1.32i，-0.76-1.32i，0.51-0.88i和0.51+0.88i，此时系统是不稳定的。

当α=2.1时：在(0，0)处，特征值为-1.05-0.16i，-1.05+0.16i，-0.97+2.77×10-16i，0.95-0.46i和-0.95+0.46i，此时系统是不稳定的；在(0，0.5)处，特征值为-0.83-1.45i，-0.83+1.45i，0.29+0.51i和0.29-0.51i，此时系统是不稳定的；在(0.167，0)处特征值为-1.05-0.16i，-1.05+0.16i，-1.003+3.05×10-16i，-0.96-0.29i和-0.96+0.29i，此时系统是不稳定的。

当α=3.6时：在(0，0)处，特征值为-1.01-0.37i，-1.01+0.37i，-0.95-0.17i，-0.83-0.48i和-0.95+0.17i，此时系统是不稳定的；在(0，0.5)处，特征值为-1.02-0.37i，-1.02+0.37i，-0.9-0.16i，-0.9+0.16i，和-0.83-0.7i，此时系统是不稳定的；在(0.167，0)处特征值为-1-0.37i，-1+0.37i，-0.99-0.17i，-0.99+0.17i和-0.87-0.5i，此时系统是不稳定的。

通过数值模拟及数学推算分析得出，当0<α<1时，均衡点在不同的阶数下均是不稳定的，也即系统是易受干扰的。因此，当时间记忆较短(小于1期)时，企业的产量决策极易受到影响。当α>1时，均衡点在不同阶数下依然是不稳定的，因此，当时间记忆较长(大于1期)时，企业间的产量决策易受干扰。

考虑到时间成本、市场变化、产品更新等因素，建议企业在最短的时间周期做出合理的决策，减少外在负面影响，提高企业产品的经济效益。

4 结论

在对传统模型的研究基础上，考虑了时间的记忆性质对决策的影响，引入分数阶理论，对双寡头市场上不同时间尺度下产量决策的稳定状态进行了分析。

为了便于分析，先对整数阶(本文的1阶)进行了分析，得出了所建双寡头模型易受到研究因素的干扰从而不稳定的结论。其次利用分数阶相关知识，对不同时间状态下的模型进行了稳定性分析,得出了不论在何种时间记忆下，模型都是非稳定的。根据此次研究和经济学中对寡头市场的已有研究，建议寡头企业间可采取协议合同，在良性定价的基础上，尽量在市场稳定的条件下，根据理论计算结果(即达到产量均衡点时)结合往期的市场产量进行产品生产，做到双方利润最大化，从而达到双赢的结果。