基于流固耦合模型的永磁耦合器导体铜盘散热研究*
2021-11-22韩雪岩朱龙飞
李 啸, 韩雪岩, 朱龙飞, 马 鑫
(沈阳工业大学 国家稀土永磁电机工程技术中心,辽宁 沈阳 110870)
0 引 言
永磁耦合器作为一种新型磁传导装置,具备软起动和调速功能,还有结构简单、节能环保等优点。但在永磁耦合器运行过程中,其主要做功部件导体铜盘中会产生大量涡流损耗,由此产生大量热量,导致导体铜盘成为永磁耦合器装置温升最高处,如果不及时将热量散出,会导致永磁耦合器整体工作受到影响[1-3]。现阶段,风冷型永磁耦合器散热方法主要有:(1)在主要做功部件导体铜盘外侧端盖处,添加导风散热片,增大散热面积,降低温升;(2)在导体铜盘外侧端盖处,进行开孔设计,将内部热量导出,降低温升。永磁耦合器是通过电磁耦合传递转矩和转速的机械设备,在运行时,端盖和导体铜盘与电机轴连接,在电机高速运行时, 若进行开孔设计,会导致盘体产生形变,使永磁耦合器整机结构机械强度降低,因此本文将采用外侧端盖添加导风散热片方法进行散热设计[4-5]。
关于永磁耦合器温度场和散热结构设计,许多学者做出了研究。文献[6]对一台小功率永磁耦合器进行散热结构研究,设计比较环形直肋和矩形直肋散热片对散热方面的影响。文献[7]研究了不同气隙长度下永磁耦合器中永磁体最高温度,气隙长度的改变对永磁体温升影响很大,同时剩磁和最大磁能积也会发生较大变化。文献[8]在原有冷却结构基础上改进永磁耦合器冷却散热结构,使温升值下降,永磁体达到安全工作温度。文献[9]提出采用双向耦合计算方法,考虑温度对磁化器性能的影响以及永磁体磁场和磁特性对温度场的影响,实现磁场和热场的耦合计算。通过试验验证了单向耦合和双向耦合的仿真结果。
本文基于流固耦合和传热学理论模型,利用有限元仿真软件对风冷型永磁耦合器的导体铜盘温度场进行仿真分析。通过样机试验与仿真结果的对比,证明了该有限元计算法的准确性;设计了3种不同结构的导风散热片,研究得到径向式结构为最佳散热结构;分析了导风散热片在不同物理参数变量下对永磁耦合器导体铜盘散热冷却的影响。通过以上计算分析,为后续风冷型永磁耦合器的散热冷却提供了参考依据。
1 永磁耦合器模型及其参数
在永磁耦合器工作中,电机带动导体盘旋转时与负载端的永磁盘发生相对运动,切割磁感线,在导体盘中产生涡流,该涡流在导体盘上生成感应磁场,由于永磁体产生的磁场与涡流产生的感应磁场之间的相互作用力,从而带动永磁盘旋转,实现能量的非接触传递。涡流损耗的产生虽可以为永磁耦合器的工作提供输出转矩,但会产生大量热量,影响装置正常工作。
因为导体铜盘侧在永磁耦合器正常运行时会产生大量热量,所以在进行散热设计研究时,仿真模型取外侧端盖、导体铜盘和散热片,其余部件进行合理简化。图1为永磁耦合器仿真模型,表1为永磁耦合器输出性能指标,表2为仿真模型尺寸参数。

图1 永磁耦合器模型

表1 永磁耦合器性能指标

表2 样机尺寸参数
2 流体场温度场数学模型
2.1 流体场分析数学模型
流体场分析主要基于质量守恒方程、动量守恒方程、能量守恒方程来建立理论基础。三大方程可写为如下形式[10-14]。
能量守恒方程:
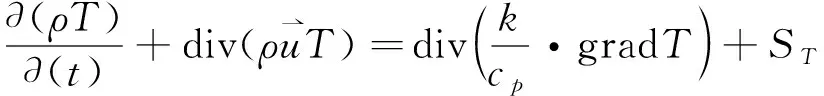
(1)
式中:T为温度;cp为流体比热容;k为流体导热系数;ST为黏性耗散项。
质量守恒方程:
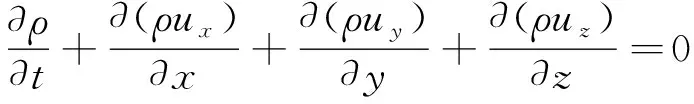
(2)
式中:ρ为流体密度;t为时间;ux、uy、uz为x、y、z方向所对应的速度分量。
动量守恒方程如下。
X方向动量守恒方程:

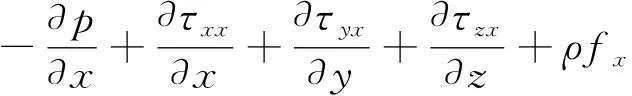
(3)
Y方向动量守恒方程:

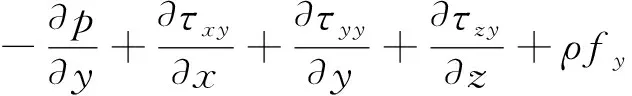
(4)
Z方向动量守恒方程:
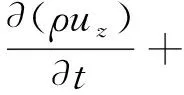
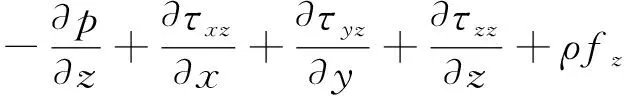
(5)
式中:ρ为流体单元上所受的压力;τxx、τyx、τzx、τxy、τyy、τzy、τxz、τyz、τzz为流体单元的剪应力分量;fx、fy、fz为流体单元在x、y、z方向所受的单位质量力。
2.2 温度场分析数学模型
当永磁耦合器正常工作时,与周围环境之间的热量交换有:热传导、热辐射、热对流,其中热辐射比重小,故本文只考虑热传导和热对流2种形式,可用以下方程表示[15-17]:
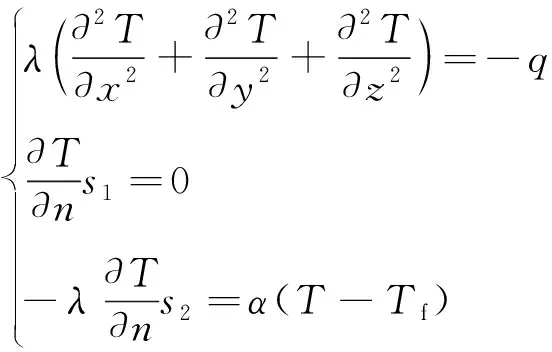
(6)
式中:λ为求解域内各种介质的导热系数;T为固体待求温度;q为热源密度;α为对流散热系数;Tf为附近流体的温度;s1、s2分别为求解域中的绝热面、散热面。
由于本文在仿真计算时,采用整体模型进行仿真,模型不存在对称面,所以s1绝热面不存在;s2面为永磁耦合器与空气接触的所有对流散热面,包括外侧端盖、导体铜盘、导风散热片。
2.3 流体域模型的建立
在永磁耦合器工作过程中,导体铜盘及端盖均在做旋转运动。因此,需在永磁耦合器整机模型外侧建立2个流体区域,即内流域和外流域。内流域设置同样转速,模拟永磁耦合器实际旋转过程。
由图2可以看出,永磁耦合器样机模型位于内流域内,外流域将永磁耦合器整机模型和内流域包裹。

图2 流体计算区域
2.4 热源的确定
永磁耦合器温度场仿真计算时,其热源设为导体铜盘的损耗数值。永磁耦合器工作运行在不同气隙长度、不同转差下,所产生的涡流损耗是不同的。通过电磁场仿真计算不同气隙长度、不同转差下导体铜盘侧损耗数值。在散热系统设计研究时,以导体盘和永磁体盘之间可调节的最小气隙长度,导体铜盘上产生的损耗数值作为热源。
由电磁仿真可得导体铜盘上产生的涡流损耗为3.296 kW。因此,由热源密度公式可得永磁耦合器温度场仿真计算所需的生热率:
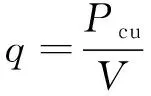
(7)
式中:V为导体铜盘的体积;Pcu为导体铜盘所产生的涡流损耗。
通过式(7)计算可得生热率为5 642 863 W/m3。
3 样机温度场计算及试验验证
3.1 有限元温度场仿真计算
永磁耦合器温度场计算使用流体场仿真软件Fluent进行。在仿真计算过程中设置初始温度为288 K,即15 ℃。仿真研究假设:(1)定常流体;(2)仿真过程中只研究热传导、热对流,忽略热辐射影响;(3)气体为不可压缩牛顿气体;(4)忽略空气重力和浮升力。
图3为永磁耦合器气隙长度为4 mm和6 mm分别对转差150 r/min和250 r/min进行仿真得到的温升云图。由图3可知导体铜盘侧温升分层明显,永磁耦合器在设计时,导体盘和永磁体盘中间间隙狭窄,内部空气流通困难,运行时产生的热量不能及时导出,导体铜盘上靠近中心处温升明显高于边缘处,因此,可在外侧端盖处添加导风散热片,增加永磁耦合器与空气接触面积,将热量快速导出,确保永磁耦合器正常工作。

图3 导体铜盘温升图
3.2 温升试验与仿真结果对比分析
样机试验流程如图4所示,将驱动侧同步电机、永磁耦合器、转速转矩传感器和负载侧磁粉制动器安装在工作台上。驱动侧电机正常工作时,通过调节装置,调节永磁耦合器导体盘和永磁盘之间气隙长度为4 mm和6 mm。当转差达到150 r/min和250 r/min时进行温升试验,用红外线测温仪测量导体铜盘的最高温度。并计算温升值,将试验所得数据与仿真数据进行比较分析。

图4 样机系统热试验实物图
表3为温升试验结果比较表,由表3中数据可知,在无冷却散热系统下,有限元温度场仿真温升值与试验温升值误差小于10%,证明了温度场有限元仿真方法有效性,为下文利用该温度场有限元法计算最小气隙长度、最大转差率下永磁耦合器导体铜盘温升值、不同冷却散热结构的设计选择,以及不同散热片物理参数的分析研究提供了可靠方法。

表3 温升值比较
4 散热影响因素研究
本文采用在端盖外侧添加散热片的方法,对永磁耦合器进行散热研究。导风散热片散热能力会被许多因素影响,本文对导风散热片的不同参数进行仿真分析,将选择重要的物理结构参数进行仿真模拟,进行单因素试验。保持其他影响因素不变的前提下,研究导风散热片单一变量因素对其散热能力的影响。
4.1 不同散热片结构设计
设计4种不同结构的散热片分别为无散热结构、径向式结构、半圆式结构、弧形式结构,如图5(a)~图5(d)所示。将不同结构散热片添加在端盖外侧,以最小气隙2 mm长度下,导体铜盘产生的涡流损耗作为热源,进行温度场仿真计算分析,仿真得到导体铜盘侧最高温度,与未加散热片导体铜盘侧最高温度比较,选择最优散热结构。
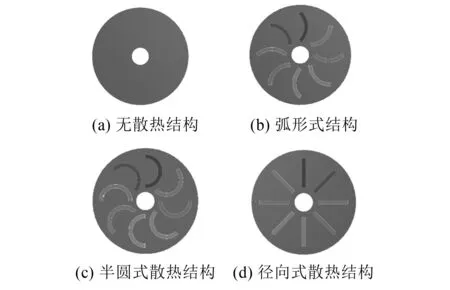
图5 不同散热片结构图
由图6最高温度云图分析可知,在无散热结构时,导体铜盘最高温度达到404.31 K,即131.16 ℃。根据永磁耦合器行业国家标准可知[18],风冷型永磁耦合器在最小气隙长度工作时,导体铜盘侧最高温度不得超过120 ℃。因此,需要添加导风散热片使永磁耦合器在安全温度工作。

图6 不同散热片结构最高温度云图
由表4可知当添加径向式时导体铜盘侧最高温度为391.1 K(118.15 ℃)、添加半圆式时导体铜盘侧最高温度为396.95 K(123.8 ℃)、添加弧形式时导体铜盘侧最高温度为395.67 K(122.52 ℃)。与无散热结构相比,添加散热片,导体铜盘侧最高温度可下降约10%,降温效果显著。但添加弧形式结构和半圆式结构散热片后,导体铜盘侧最高温度仍然高于国家标准的最高温度120 ℃,因此选择径向式结构为最佳散热结构。
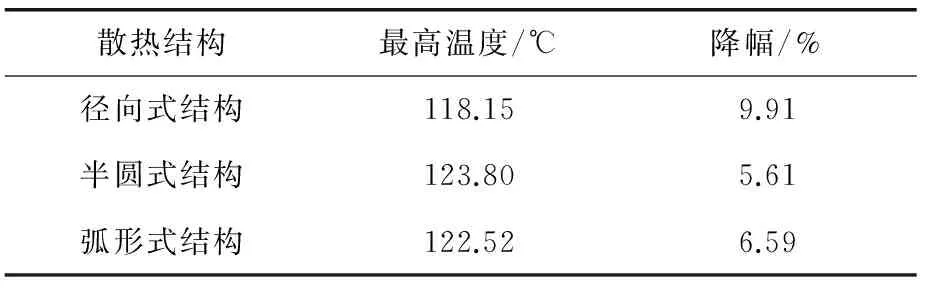
表4 不同结构温度降幅
4.2 散热片高度及整体阻力矩比较分析
选择径向式散热片结构,研究不同高度散热片对散热效果的影响。仿真过程中,设定径向式散热片厚度、散热片个数完全相同。在20~56 mm的设计高度范围进行等距划分,以4 mm为间隔划分共计10组模型。导入Fluent,进行温度场有限元仿真。
计算可知,散热片高度每增加4 mm,永磁耦合器导体铜盘的温升值下降2%~12%,温升值降幅最高为12.19%。且此时导体铜盘最高温度均低于120 ℃,符合风冷永磁耦合器导体铜盘安全工作温度标准。散热片高度增加对永磁耦合器的热量导出起着良好的效果。但由图7可以看出,散热片高度的增加,同样对整体阻力矩上升幅度产生影响。散热片高度不可无限增加。由图8数据可知,在32~36 mm高度范围内,导体铜盘温升值下降明显,继续增加高度,温升值下降幅度将低于5%,且阻力矩上升34.2%。因此散热片高度取值可选择在32~36 mm区间内。
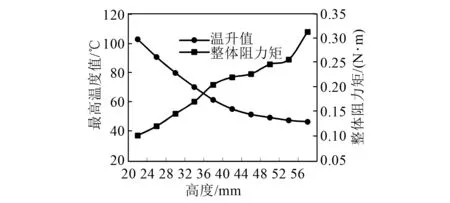
图7 温升值及阻力矩随高度变化趋势图
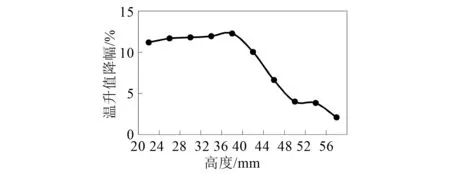
图8 温升值随高度降幅图
4.3 散热片厚度及整体阻力矩比较分析
确定散热片合适高度范围后,改变散热片厚度研究此因素对永磁耦合器导体铜盘侧散热的影响。仿真过程中,设定径向式散热片高度、个数完全相同。在5~14 mm的设计厚度范围进行等距划分,共计10组模型,进行建模网格剖分,导入Fluent进行仿真。
由仿真分析可知,随着散热片厚度每增加1 mm,导体铜盘温升值下降了4%~13%,最高降幅可达13.12%,且最高温度符合国家标准,降温效果良好。由图9可知,由于整体阻力矩的限制,散热片厚度不可无限增加。由图10可知,当散热片厚度范围在5~7 mm区间时,导体铜盘降温幅度大,继续增加厚度,温升值下降幅度低于4%,因此散热片厚度取值范围为5~7 mm区间。

图9 最高温度及阻力矩随厚度变化趋势图

图10 温升值随厚度降幅图
4.4 散热片个数及整体阻力矩比较分析
仿真过程中,设定单一研究变量为散热片个数,径向式散热片高度、厚度取值完全相同。研究不同个数散热片对导体铜盘温升的影响。端盖外侧分别设计添加4、6、8、10、12、14个散热片。共计7组模型,进行建模网格剖分,导入Fluent进行温度场仿真计算。
由图11可知,散热片个数每增加2个,导体铜盘最高温度下降12%~13%,此时导体铜盘最高温度均低于120 ℃,增加个数对热量的导出有着良好的效果,但整体阻力矩上升较为明显,由此可知,散热片个数不可无限增加。由图12可知,当散热片个数为8个时,温升值降幅最低为13.54%,继续增加散热片个数,整体阻力矩上升了12.6%。在对散热片个数进行合理取值时也需要考虑到温升值、整体阻力距,以及材耗、经济性能等多方面因素。因此,最终散热片个数合适取值为8。
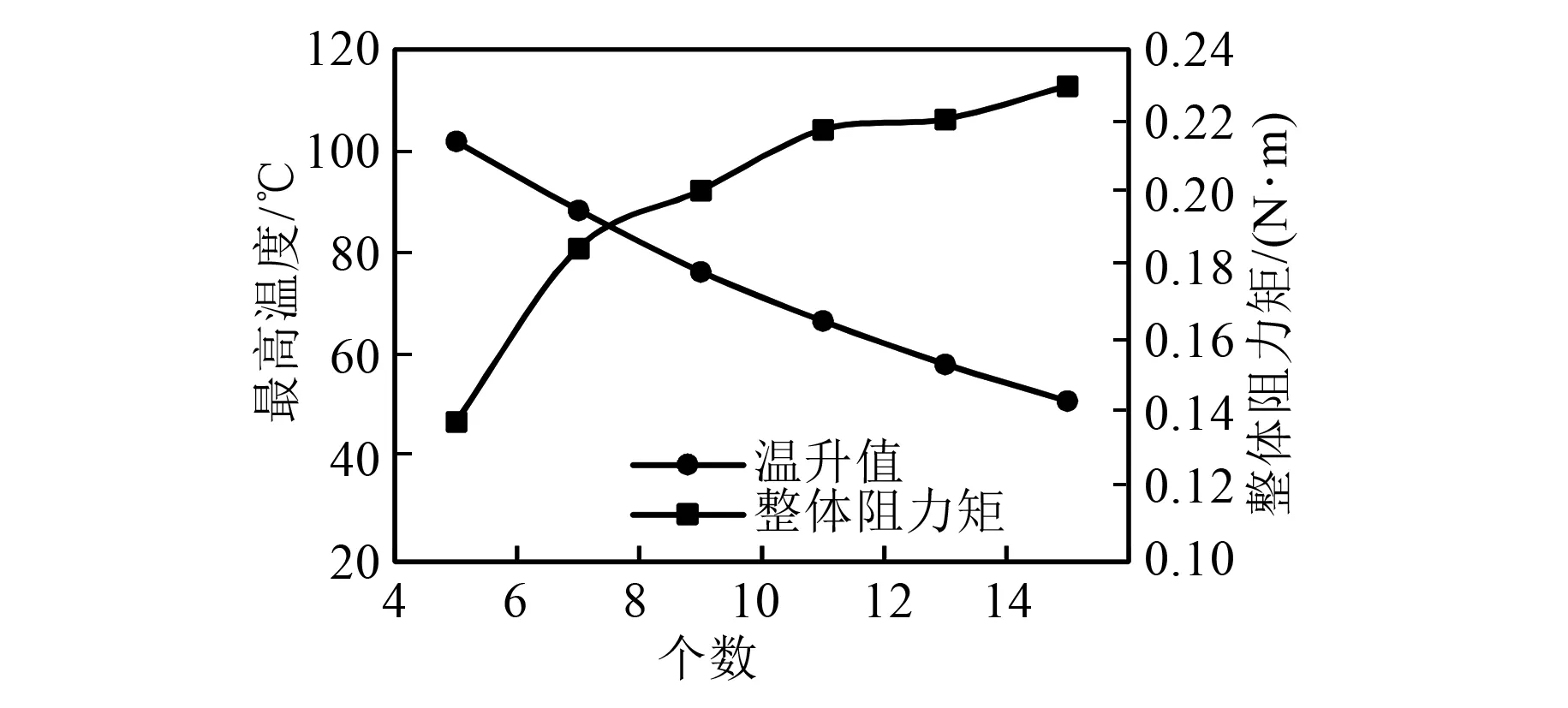
图11 最高温度及阻力矩随散热片个数变化趋势图
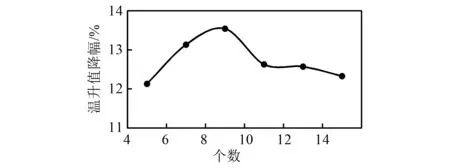
图12 温升值随散热片个数降幅图
4.5 径向式散热片对风速的影响分析
由图13可知,当添加径向式导风散热片后,与无散热结构相比,导体铜盘内侧热量集中的位置,其流速增大,且越靠近外圈,空气流动速度越快,在最外圈时空气流动速度达到最大值37.35 m/s。流速增加了34.1%。
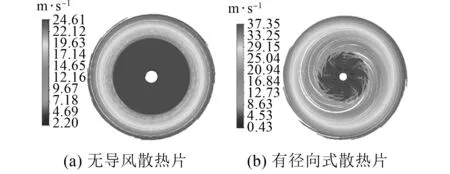
图13 优化前后流迹线图
流速的升高可使导体铜盘温度降低,提高此处的对流换热系数,使导体铜盘内部热量更快速地从散热片导出,降低温升值。本文导风散热片安装于永磁耦合器端盖外侧外圈空气流动速度较大区域,可以使散热效果更好。
5 结 语
本文基于流固耦合模型对一台适用于15 kW永磁电机工作场合、小功率风冷型永磁耦合器导体铜盘温度场进行仿真分析,设计了不同结构以及分析不同变量因素对冷却效果的影响。得出如下结论:
(1) 在无散热结构时,实际样机试验与有限元仿真相比较,误差小于10%,证明了基于流固耦合模型下有限元仿真准确有效。当本文所用永磁耦合器添加径向式散热片后,最高温升值下降了9.91%,研究可得径向式散热片结构对于降低温升,导出热量具有一定效果。
(2) 不同变量因素对散热效果的影响很大,径向式散热片高度、宽度、个数的增加可以有效降低温升,最高降幅可达13.54%,效果明显,为风冷型永磁耦合器散热结构设计提供了一定参考。
