不对称磁障对IPMSM电磁振动噪声的影响分析
2021-11-22申合彪赵朝会陆海玲
申合彪, 赵朝会, 陆海玲, 庞 亮
(上海电机学院 电气学院,上海 201306)
0 引 言
内置式永磁同步电机(IPMSM)相较于表贴式电机,不仅具有永磁转矩,还拥有磁阻转矩,这使其具有更大的功率密度,更高的效率,广泛应用于电动汽车、家用电器、工业领域。然而IPMSM同样带有较大的转矩脉动及齿槽转矩的缺点,这将会引起电机的电磁振动与噪声,不适合一些精度要求高的伺服系统。因此,研究降低IPMSM的转矩脉动,或者抑制电机的电磁振动与噪声成为其性能优化的主要研究方向。近些年,国内外学者针对这2个方向做了大量研究。
永磁电机降低齿槽转矩或者转矩脉动的方法主要包括定子斜槽[1]、定子齿开辅助槽[2]、转子表面开辅助槽[3]、转子轴向分段[4]、磁极偏心[5]等,缺点是均难以保证电机的功率密度。文献[6-7]采用优化转子隔磁桥的方法来抑制电机的径向电磁力波,通过对比优化前后电机的电磁噪声声压图证明优化方法的有效性。文献[8]提出了定子齿顶偏移的方法来降低定子齿中间位置的电磁力幅值,并且优化了偏移距离使降噪效果达到最佳。文献[9]针对IPMSM,采用转子外表面上开辅助槽的方法削弱空间阶次电磁力幅值,降低电机振动噪声。以上优化方法虽然有效地通过降低径向电磁力幅值来削弱振动噪声,但输出转矩同样均有不同程度的降低,使得电机的功率密度下降。
因此,有学者在寻找一种内置式永磁电机的优化方法——既能达到优化电机转矩脉动的目的,又能保证电机的功率密度不降低。文献[10]对比分析了传统转子轴向分段结构和不对称磁障结构2种优化方法下的电机性能。结果表明,采用不对称磁障结构不仅有效削弱了齿槽转矩与转矩波动,还会增大电机的输出转矩。文献[11]提出了一种辅助磁障结构应用于IPMSM,通过优化辅助磁障的尺寸参数使电机的永磁转矩和磁阻转矩错开一定的角度,从而提升合成输出转矩平均值,并且降低了转矩脉动。文献[12]针对内置式电机提出定子槽口不对称、转子磁障不对称2种优化方法,二者均有效降低转矩波动,达到电机的设计要求。但这些不对称磁障的优化方法大多数只以转矩脉动、齿槽转矩为优化目标,比较片面。而永磁电机的电磁振动噪声主要由电机的转矩脉动与径向电磁力波动引起[13],本文探讨不对称磁障的方法在降低转矩脉动、保证电机功率密度的情况下,对电机的径向电磁力波、电磁振动噪声的影响。
1 电机电磁分析
本文以一台6极36槽内置式V型永磁同步电机为研究对象,图1为原始电机横截面图,电机基本参数如表1所示,图2为电机转子结构采取不对称磁障示意图。根据电机参数建立电机的有限元仿真分析模型,添加三相对称电流激励,对电机进行电磁分析。

表1 电机基本参数

图1 电机横截面示意图
图2中,原始电机磁障长度L1为3 mm,延长每极单侧磁障长度L1,电机转子由上下2部分组成且沿中线对称,从而使转子上下2部分产生的转矩相互偏移一定的电角度,进而降低转子整体合成转矩的波动。图3为磁障长度L1与转矩波动变化关系图。可以看出随着L1的增加转矩波动逐渐减小。考虑到模型干涉问题,选取磁障长度L1为7 mm。

图2 不对称磁障电机横截面示意图

图3 磁障长度与转矩波动变化曲线
1.1 径向电磁力理论分析
根据麦克斯韦张量法,作用于定子铁心内表面的径向电磁力密度为

(1)
式中:fr为径向电磁力密度;Br、Bt分别对应电机气隙磁通密度的径向与切向分量;μ0为真空磁导率,μ0=4π×10-7;由于气隙磁通密度的径向分量远大于切向分量,可忽略其切向分量的平方项。
转子永磁磁场气隙磁通密度BRδ,与定子电枢反应磁场在气隙处的磁通密度BSδ2部分叠加组成电机气隙磁通密度,因此式(1)可表示为[14]:

(2)
电机永磁气隙磁密和电枢反应气隙磁密为其对应的磁动势和气隙磁导的乘积可表示为
BRδ=FRλδ
(3)
BSδ=FSλδ
(4)
式中:FR为永磁磁场气隙磁动势;FS为定子电枢反应磁动势;λδ为等效气隙磁导。FR、FS与λδ可表示为[14]

(5)

(6)

(7)

将式(3)~式(7)代入式(2)可归纳出永磁磁场和电枢反应磁场在定子齿表面产生的主要阶次为(vR±vS)p,频率为(vR±1)f1,f1为电机基波频率。根据此规律列出本文所研究样机的电磁力波阶数v及其频率倍数f,如表2所示。
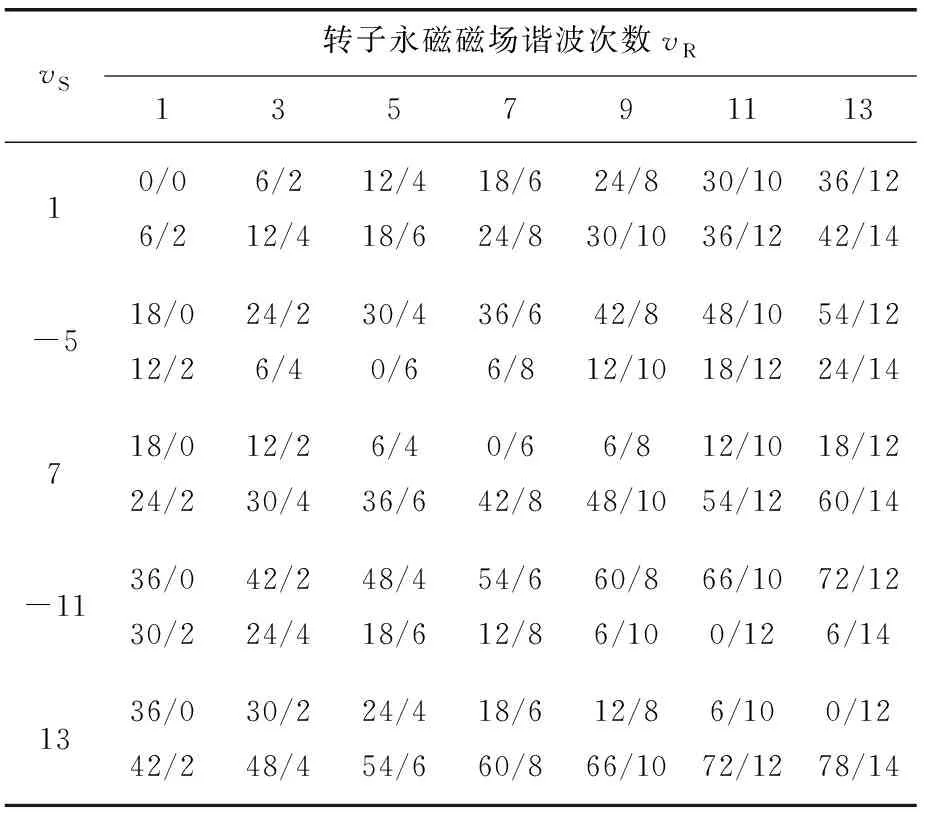
表2 永磁磁场和定子电枢反应磁场产生径向电磁力阶次与频率
1.2 电机电磁有限元分析
根据建立的原始电机与对称磁障电机的有限元分析模型,仿真得到其对应的电机负载运行时输出转矩如图4所示。

图4 电机输出转矩对比图
由图4可知,电机转矩波动由12.5%降低为7.4%,而且不仅没有牺牲输出转矩,还将平均转矩增大了约1 N·m。可见采用不对称磁障的方法提升了电机的功率密度,有效降低了转矩波动。
图5给出了采用不对称磁障前后电机的磁力线分布图,可以看出原始电机磁力线分布图具有周期性且空间周期为6,这与电机的极数是对应的。当采用不对称磁障结构时磁场的周期性将消失,不对称磁障结构产生了不平衡磁拉力,电机存在空间一阶电磁力分量。

图5 电机磁力线分布对比图
取电机气隙处圆形路径作为径向电磁力波的观测路线。由前文可知径向电磁力是关于时间和空间变化的函数,图6为周期性分布电机径向电磁力密度的时间-空间分布云图。对其进行快速二维傅里叶分解可得径向电磁力密度的空间与时间谐波分量如图7所示。

图6 径向电磁力密度时空分布

图7 原始电机径向电磁力密度二维傅里叶分解图
由图7仔细分析,可以发现电机径向电磁力分布规律与表2的解析一致。且(0,0f1)、(6,2f1)、(12,4f1)分量幅值较大,分别为2.356×105、2.736×105、4.251×104N/m2。由于(0,0f1)为直流分量,只会使电机定子产生形变并不会引起电机的电磁振动和噪声。电磁振动噪声与电磁力波空间阶次的 4 次方呈反比,高阶空间径向电磁力波引起的振动噪声可以忽略,一般只需关注空间阶数小于8阶的分量即可。值得注意的是虽然(0,12f1)的幅值为1 991 N/m2远远小于(6,2f1)分量的幅值,但是此分量阶次为0阶仍有可能对电机振动噪声产生重大影响。
由图8分析知,(0,12f1)、(6,2f1)电磁力分量幅值分别为907.5 N/m2、2.707×105N/m2相比于原始电机模型,各自对应的分量幅值下降幅度为54.4%、1%。由于转子磁障的不对称结构,引起了幅值较小的奇数次基波倍频电磁力分量。其中(1,12f1)相较于原始电机为新增加电磁力分量,幅值为1 058.4 N/m2。由此可见不对称的转子结构使电机产生了不平衡磁拉力,存在空间一阶电磁力分量,这与电机磁力线周期性的变化分析结果是吻合的。

图8 不对称磁障电机径向电磁力密度二维傅里叶分解图
2 模态分析
当电机径向电磁力波频率与电机固有频率等于或接近时,将引起共振现象[15]。这不仅会产生较大的电磁噪音,还会对电机的整体寿命产生不利影响,因此通过对电机结构进行模态仿真,来分析电机固有频率尤为重要。由于电机的电磁振动噪声主要是由气隙处的径向电磁力作用在电机定子齿部产生的,振动的发生部位主要是定子,忽略绕组对定子模态的影响。而且本文采用的不对称结构是在转子上进行改动,并不会影响定子模态的固有频率。因此,本文采用计算精度较高的有限元法对电机定子结构进行模态仿真分析,图9为电机定子铁心各阶模态振型及固有频率。

图9 电机定子结构模态振型图
由表2分析可知,原始电机的径向电磁力频率为电机基波频率的偶数倍。与有限元模态分析得到的固有频率对比,可发现原始电机的径向电磁力与定子低阶模态固有频率相差较远,因此电机不会发生共振。当电机采用不对称磁障结构时,结合前面电磁力二维傅里叶分解可知,不对称结构产生的电磁力分量频率不仅具有电机基波频率的偶数倍,同时还存在奇数倍,这将增加电机气隙处径向电磁力频率与定子模态固有频率接近的概率,增大电机发生共振的风险。
3 振动响应分析
建立原始电机与不对称磁障结构电机的振动响应模型,将前文仿真得到的随时间变化的径向电磁力加载到3D定子模型齿上,设定约束条件及求解设置。可得到电机机壳表面振动加速度频谱曲线如图10所示。

图10 电机振动加速度频谱图
由图10可知,(1)原始电机的振动加速度幅值分别在300、600、900、1 200、1 500、1 800 Hz频率附近较大,这些频率对应电机2、4、6、8、10、12倍基波频率。由前文知这些频率点的电磁力幅值较大,引起的振动响应比较明显;(2)原始电机在2f1=300 Hz与12f1=1 800 Hz频率处的振动加速度尤为突出,由电磁力的二维傅里叶分解图知,对这2处振动加速度起主要贡献的电磁力分量为(6,2f1)、(0,12f1)。虽然(0,12f1)分量幅值较低,却仍引起了较大的振动,不可忽视此分量;(3)采用不对称结构后除了基波的偶数倍频的振动响应明显,奇数倍频的振动响应同样突出,这是由奇数倍频电磁力分量激发出来的。且7f1=1 050 Hz频率处的振动加速度数值较大,将在此频率点引起较大振动噪声。
4 噪声分析
建立一个用于计算电磁噪声的球形空气域模型,将上一步电机振动响应分析的加速度结果作为噪声分析激励源,加载到提取的电机结构表面形成的包络面上。定义球形模型外表面为仿真边界,并选取这个面进行观测,生成原始电机与不对称磁障电机的声压级(SPL)对比曲线图如图11所示。

图11 电机SPL频谱图
由图11可得到以下结论:(1)原始电机的 SPL 值在偶数倍基波频率下比较大,这是由于这些频率点下的振动加速度较大,相对应引起了较大的噪声值。且在300 Hz与1 500 Hz下SPL值尤为突出。(2)不对称磁障电机的SPL值除了在2f1=300 Hz下比较大,而且在7f1=1 050 Hz、9f1=1 350 Hz、11f1=1 650 Hz奇数倍频下噪声幅值也较突出,这是由于不对称结构激发出的奇数倍基波频率处的径向电磁力分量导致的,且与不对称磁障电机的振动加速度的分析结果相吻合。(3)原始电机与采用不对称磁障电机相比,SPL平均值由56.8 dB增大为67.1 dB。
5 结 语
本文以一台37 kW的IPMSM为研究对象,对比分析了当采取不对称磁障结构后,电机的转矩波动、径向电磁力分量、定子振动加速度、电机电磁噪声的变化情况。根据仿真结果,可以得到以下结论:
(1) IPMSM主要产生偶数倍基波频率的径向电磁力分量,采用不对称磁障结构后的电机,不仅产生偶数倍频的电磁力分量,还产生奇数倍频电磁力分量。导致这些频率点的振动加速度增大,提升了电机发生共振的风险。
(2) 虽然(0,12f1)径向电磁力分量幅值与(6,2f1)、(12,4f1)分量幅值不在同一数量级,但仍对电机振动噪声起重大影响,不可忽视此分量的作用。
(3) 不对称磁障电机虽然保证了电机的功率密度不被牺牲,且有效降低了转矩波动,但增大了电机奇数倍基波频率处的电磁噪声,导致电机的SPL的平均值反而由56.8 dB增大为67.1 dB,设计时需综合考虑。
