储能支撑光伏参与电网一次调频的优化控制策略研究

傅质馨，张晶晶，崔晓丹，吴家龙，朱俊澎，袁越

（1.河海大学，江苏南京 211100；2.南瑞集团国网电力科学研究院，江苏南京 211106；3.河海大学可再生能源发电技术教育部工程研究中心，江苏南京 210098）

0 引言

随着电网中光伏渗透率的大幅增加，故障扰动下的系统频率调节特性逐渐恶化。为了提升光伏的利用率，光伏发电一般工作在最大功率点，不提供惯量支撑，也未考虑必要的容量备用，因此对电网的频率支撑作用有限[1]。考虑到对系统的主动支撑作用，光伏发电参与系统调频就尤为必要。另外，从利用新的支撑手段角度，发挥储能快速灵活响应特性，开展储能支撑光伏并网调频策略研究，有利于发挥系统综合效益，在提高系统频率稳定的同时，提升新能源的利用率。

目前，对光伏参与调频的研究主要有以下两个方面：一是利用虚拟同步控制策略，使光伏发电具有下垂、惯性特性，模拟同步发电机组参与调频；二是控制光伏输出电压，使其不在最大功率点运行，留有一定的减载调频备用[2]，[3]。储能系统能通过功率变换装置实现功率的四象限灵活调节，迅速响应频率变化。当前，关于储能辅助电网一次调频的控制策略研究，主要关注储能电池的选型与容量配置、储能参与调频的经济性分析、利用单一虚拟下垂控制和协调虚拟惯性控制参与调频[4]～[10]。在光储联合参与调频方面，文献[11]提出了利用逆变器的空闲容量参与调频，其结果显示加装储能的光伏电站的收益大于光伏电站采用减载调频时的收益。文献[12]对光伏和储能的逆变器控制策略进行改进，提出光伏三段式控制策略，但第二段时序切换没有考虑到和储能的配合。

综上所述，现有光伏调频策略对于实现附加有功环节控制系数与减载备用容量动态匹配，储能调频控制策略中的调频参数设置灵活性及自适应性等问题，尚无理想的解决办法。

储能不仅能够平滑光伏的功率波动，还可以弥补光伏单独参与调频的不足。本文首先提出了光伏和储能参与电网一次调频的策略：光伏采用了一种跟随系统出力及频率偏差变化的可变减载调频策略；储能采用一种跟随荷电状态、频率变化率和频率偏差变化的自适应控制策略。为了减少光伏固定减载造成的功率损失，降低储能系统成本，采用了光伏可变减载和配置储能联合调频的策略，由储能为电力系统频率初始变化阶段提供惯性响应，光伏利用可变减载运行和储能联合参与一次调频。本文利用IEEE三机九节点系统，对所提出的策略进行了仿真验证。

1 光伏发电参与电网的一次调频策略

1.1 光伏发电控制系统

光伏发电系统主要由光伏阵列、Gboost变换器、并网逆变器、滤波器和控制系统组成（图1）。光伏阵列输出的电压Vpv和电流Ipv经最大功率跟踪（MPPT）控制器后，产生直流电压参考值Vrefmppt。Vrefmppt和Vpv的误差信号，经积分后得到光伏输出有功功率给定Pref。Pref和Boost变换器高压侧的有功功率Pdc比较，经PI控制和脉冲宽度调制（PWM）后生成信号Gboost，驱动Boost变换器工作，从而实现光伏阵列的MPPT控制。逆变器的控制主要由电流内环和功率外环组成。通常情况下，逆变器工作在单位功率因数状态，即i*gq=0。电容电压udc与电压参考值uref作差后，通过PI控制生成电流内环参考值igd*；再与采样所得的实际电流值igd，igq作差，经PI控制器和电流解耦控制后，得到电压给定值uiq，uid。最后，经过坐标变换通过PWM得到逆变器的触发脉冲Sg，实现逆变器有功无功的解耦控制及并网运行。

图1 光伏发电系统示意图Fig.1 Schematic diagram of PV power generation system

1.2 光伏可变减载调频策略

由图2所示的光伏输出P-V特性曲线可知，光伏系统一般通过MPPT控制保持最大功率输出（a点）；当光伏系统有备用容量需求时，也可以让光伏阵列处于限功率运行（b点）。

图2 光伏减载示意图Fig.2 Schematic diagram of photovoltaic power reserve

光伏系统的减载率σ：

类比常规机组的调频控制原理，光伏系统参与调频的两个条件：①具有一定的备用容量；②负荷扰动时能够实时响应系统频率变化而增减出力。基于以上两点，本文将光伏电站在负荷扰动下的调频出力与系统频率偏差和光伏最大有功出力建立动态联系，采用的光伏调频控制策略如图3所示。光伏采用MPPT控制后得到最大有功输出PMPPT，经过可变减载控制并限幅后，作为光伏阵列新的有功功率给定Pref，输出给Boost变换器控制系统。

可变减载控制特性曲线表达式：

式中：K0为初始情况下的减载率；PMPPT为光伏在当前工况下的最大有功功率；PN为光伏在标况下的额定有功功率；Δf为系统频率偏差；Δfmax为系统允许的最大频率偏差，取Δfmax=0.5 Hz。

根据式（2），可变减载控制中减载率的变化曲线如图4所示。光伏初始减载率越大，可以参与调频的容量越多，但过大的减载率会造成正常工作下的功率损失。当系统出现频率上升时，减载率越大，光伏减出力的能力越弱。为提高光伏发电的利用率，在初始减载率K0设置一定时，实际减载率σ和当前工况下光伏最大出力PMPPT成正比。当系统发生频率下降时，Δf为负，减载率随频率偏差负增大而变小，光伏阵列增发有功出力。当系统发生频率上升时，Δf为正，减载率随频率偏差正增大而变大，光伏阵列减少有功出力，动态响应电力系统频率变化参与一次调频。光伏可变减载调频控制策略：一方面当系统发生故障扰动时，控制系数σ能够实时响应系统频率波动，跟随系统频率偏差和最大有功出力而动态变化；另一方面反向调节了光伏系统的减载率，从而使光伏增减出力参与一次调频。本文提出的控制策略避免了文献[12]所使用的减载和下垂控制策略出现的下垂特性斜率的选取问题，具有灵活的自适应性。

图4 减载率变化曲线Fig.4 Load reduction rate variation curves

2 电池储能参与电网的一次调频策略

2.1 储能及其控制系统

储能及其控制系统如图5所示。Buck-Boost变换器实现储能的充放电切换，通过采样储能输出的电池功率Pbat和给定的有功功率Pref作差，经PI控制器和PWM变换后得到切换储能充放电的触发脉冲GBuck，GBoost。并网变换器的主要控制原理和光伏发电系统类似，此处不再赘述。

图5 储能系统示意图Fig.5 Schematic diagram of energy storage system

2.2 自适应下垂控制策略

虚拟下垂控制的原理是模拟同步发电机参与一次调频的频率下垂特性，其响应计算式为

式中：ΔPbess为储能调频增发的有功功率；Kb为下垂系数。

传统下垂控制采用固定的下垂系数，在系统发生短时负荷扰动或者储能电池电量充足时，调频效果好。然而，在长时负荷扰动时，储能的容量很快到达上下限，既影响了电池服役周期，又可能导致储能退出时频率的二次跌落问题。

本文根据电池储能荷电状态（SOC）动态调整下垂系数（充放电系数），既可以很好地维持SOC，防止过充过放导致的寿命变短，又可以减小储能越限时对系统造成的影响。本文采用锂离子电池储能，按SOC将其分为5个区间：工作的最大限值Smax、正常工作的上限值Shigh、正常工作的下限值Slow、工作的最小限值Smin（图6）。不同电池的充放电特性各异，均取决于其自身特性。为定量分析SOC变化时电池储能相应的出力情况，参考文献[8]，分别将取值设为0.90，0.55，0.45，0.10。

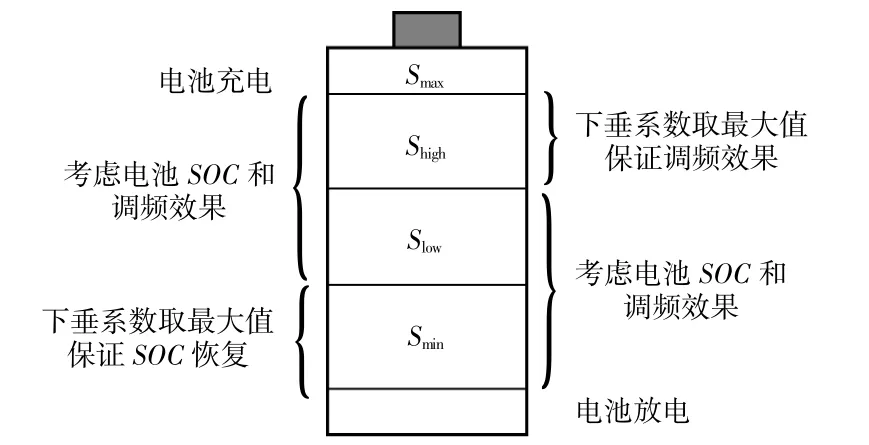
图6 电池储能工作区间设置Fig.6 Working range setting of battery storage

Logistic函数具有天然的指数性、凹凸性和饱和性。本文利用Logistic函数对下垂系数进行自适应控制，使储能的自适应策略可以兼顾调频和SOC保持效果。曲线函数表达式：

式中：K为终值；P0为初始值，P0值越大，达到饱和的时间越短；r为衡量曲线增长快慢的指标，r越大，增长越快。

以储能放电为例，当储能容量充足时，曲线呈上凸形，保证下垂系数处于一个相对更大的值；当储能容量不足时，曲线呈下凸形。随着SOC的下降，放电速度变慢，下垂系数处于较小的值，以保持SOC效果。以Ssoc为自变量，P0，r为参变量，充放电系数为因变量，构造如下等式。

电池放电：

电池充电：

式中：Kmax为下垂系数的终值；Ssoc为储能当前的荷电状态；Kbc，Kbd分别为充放电时对应的下垂系数。

当P0，r分别变化时的Kb曲线如图7所示。由图7可见，当P0，r过大时，Kb仅在一小段范围内随SOC有较大的变化，自适应能力比较弱；当P0，r变小时，Kb随SOC的变化越敏感。为了兼顾储能的调频能力与SOC维持效果，对Kb进行适当选取。以储能放电为例：在SOC大于Shigh时，使系数随着SOC变化，仍处于一个相对较大值；在SOC小于Slow时，更多地考虑SOC维持效果，控制系数变小。综合考虑上述因素后，本文取P0=0.02，r=8。

图7 控制系数Kb随P0，r的变化曲线Fig.7 Variation curves of control coefficient Kb with P0 and r

本文基于Logistic函数的特点，利用对称性，在充放电区间内仅各设置一个函数，并采用SOC分区自适应调节下垂系数。这样，不仅充分利用电池储能的调频能力，还兼顾了SOC的保持效果，规避了复杂的分段函数。

2.3 自适应虚拟惯性控制

虚拟惯性控制策略模拟同步发电机的惯性响应过程。惯性响应公式：

式中：Mb为惯性系数。

在初始扰动阶段，df/dt较大，而Δf较小，仅靠下垂控制无法满足调频需求。加入正虚拟惯性控制后，可以在降低初始频率变化率的同时，在一定程度上降低最大频率偏差。正虚拟惯性的响应时间较短，可不考虑储能的SOC，其响应公式为

式中：Mbp为正虚拟惯性系数；Mbp-c，Mbp-d分别为储能充、放电时的正虚拟惯性系数；Mp为随频率偏差变化的调节因子；c1为正虚拟惯性系数初始值；n为参变量；Dp为正虚拟惯性频率变化率死区。

由图8可知，Mp的大小和变化速率与n的取值有关，n值过小，则Mp值较小，正虚拟惯性能力不能得到充分发挥；n值过大，Δf略有增大时，导致Mp急剧增大，频率曲线会发生抖动。经过综合考虑后选择n=6。与固定惯性控制系数相比，本文提出的正虚拟惯性策略能兼顾到初始频率变化率大，然后逐渐变小，直到最大频率偏差点处变化率变为零的特点。在初始阶段的正虚拟惯性系数取稍小一点，在最大频率偏差点附近取稍大一点，使储能均匀出力，同步改善初始频率变化率和最大频率偏差。

图8 不同n时的调节因子MPFig.8 Regulatory factor MP with different values of n

然而，当频率偏差达到最大并开始进行频率恢复时，频率变化率的极性发生改变。正虚拟惯性的响应出力与调频需求方向相反，如果不加以修正，对系统来说将是一个新的扰动，不利于电网频率的恢复[8]。因此，要切换成负虚拟惯性控制，负虚拟惯性的作用时间较长，须考虑储能的SOC。响应公式如下：

式中：Mbn为负虚拟惯性系数；Mbn-c，Mbn-d分别为充放电时的负虚拟惯性系数；b1为负虚拟惯性系数初始值；Mb1为关于频率偏差变化的调节因子；fmax为电网允许的最大频率偏差幅值，取fmax=0.5 Hz；fbess-d为储能调频死区，取fbess-d=0.03 Hz。

图9为负虚拟惯性控制自适应曲线。

由图9（a）可知，当n过大时，Mb1随着频率偏差先急剧变小，后缓慢减小，不利于负虚拟惯性控制能力的利用；n变小时，Mb1减小的趋势逐渐趋于线性平稳。本文经过综合考虑，取n=2。

图9 负虚拟惯性控制自适应曲线Fig.9 Adaptive curves of negative virtual inertia control

在放电时，负虚拟惯性系数Mbn-d随SSOC及Δf的变化曲线如图9（b）所示。当SOC较高时，负虚拟惯性系数大，可充分发挥储能的快速调频能力；当Δf变小时，负虚拟惯性系数变小，兼顾了储能的SOC的稳定。

本文提出的负虚拟惯性策略考虑到频率恢复阶段的最大频率偏差大，但是频率变化率低，此时可以选择较大的负虚拟惯性系数，加速系统的频率恢复。随着时间的延长，频率偏差减小，储能的SOC值降低，此时选择较小的系数，保证储能的SOC的维持效果。

2.4 电池储能参与一次调频自适应控制策略

综合考虑储能的调频效果和荷电状态，结合下垂控制及惯性控制的特点及优势，本文提出一种基于SOC和调节因子反馈的储能自适应控制策略（图10）。

图10 储能参与一次调频自适应控制策略Fig.10 Adaptive control strategy of energy storage participating in primary frequency regulation

①首先设置储能的调频死区。为充分发挥储能快速调频的特点，将储能调频死区设置在常规机组死区的范围内，取fbess-d=0.03 Hz。

②当电力系统频率偏差Δf超过储能调频死区后，在一次调频时间内，通过下垂控制参与调频，将Δf由变下垂系数变换叠加到储能的有功控制环路中。

③当频率变化率df/dt＜0时，频率进入初始跌落阶段，此时选择正虚拟惯性控制。当频率变化率超过正虚拟惯性控制死区后，将df/dt由惯性系数变换叠加到储能的有功控制环路中。

④当df/dt由小于0转换为大于0时，频率进入恢复阶段，此时利用负虚拟惯性控制将df/dt经过负虚拟惯性系数叠加到储能的有功出力中。

当储能须要吸收功率，即Δf＞0时，控制方法和上文类似。

3 储能支撑光伏参与电网一次调频策略

储能装置性能稳定。在光伏电站中配置储能装置，利用其可快速充放电的特性，平滑光伏出力，降低系统发生负荷扰动时对系统频率的影响，可以提升整个系统的频率稳定性[13]。

不同于常规机组，光伏和储能本身不具备惯性响应和一次调频能力，在附加调频控制策略后，这两部分没有明确的阶段分界[14]。基于惯性响应控制主要用于解决频率变化率的问题，一次调频主要用于解决频率偏差问题。本文根据常规机组的频率调整特点，使光伏电站能够和常规机组具有类似的调频特性，按照光伏和储能策略的特点，将二者的联合运行分为两个时序：①储能系统为电网频率变化初期提供与常规同步发电机组类似的惯性响应；②光伏利用可变减载调频策略和储能自适应控制策略联合参与一次调频。

电网运维准则规定，特殊情况下系统频率在短时间内可能上升至51 Hz或者下降至48 Hz，故同步发电机转速一般在小范围内变化[15]。以频率下降分析，同步发电机转子的转速为0.96～1.00 p.u，可以释放的动能为

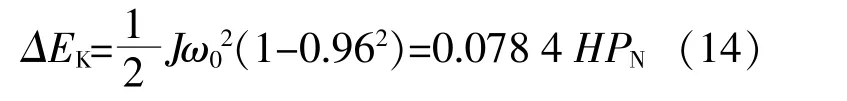
电池储能系统能够实现大范围的功率吞吐，因而较小的容量即可实现和常规机组相同的调频效果。由于电池储能充放电时间一般大于惯性响应时间，故当储能功率满足要求时，容量也就满足要求。文献[16]显示，当配置有储能的光伏电站取代同容量同步发电机组并入电网时，对储能的功率容量大小设置如下。

设储能系统在Δt内释放出的能量与转子动能相同，则有：

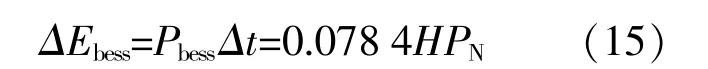
发电机组的惯量常数H≈5 s，设Δt=2 H。

式中：ω0为同步电角速度；ΔEbess，Pbess分别为储能的容量和功率；PN为发电机的额定功率；H为惯量常数；J为惯性时间常数。

由式（16）可知，当配置储能为光伏电站额定功率的3.92%时，可以实现和同容量同步发电机组类似大小的惯性响应。考虑一定的调节裕度，本文选取PN的5%作为储能的额定功率。

4 仿真及结果分析

基于IEEE 3机9节点典型系统搭建PSCAD仿真系统模型，如图11所示。其中，水电机组G1、火电机组G2，G3均配备调速器，总额定容量为567.5 MVA，总负荷量为315+j115 MVA。首先在Bus8母线分别接入光伏和储能，验证本文所提策略的有效性；然后将光储联合投入运行，仿真并验证储能支撑光伏参与电网一次调频策略的优越性。光储联合参与电网调频模型如图12所示。

图11 仿真算例系统主接线示意图Fig.11 Schematic diagram of the main wiring of the simulation example system

图12 光储联合参与电网调频模型Fig.12 Power grid frequency regulation model of PV-ES system

4.1 光伏调频策略验证

系统频率上升和下降的情况相似，而且光伏并网频率向上波动的允许范围小于向下波动的范围。因此，本文主要针对频率跌落事件进行仿真分析。

在图11的Bus8母线处，接入90 MW的光伏等值电源，3 s时增投16 MW的负荷。仿真标况下，设定光伏不参与调频、光伏采用可变减载控制策略（K0分别为5%和10%）等3种情况。由图13可见，当光伏不参与调频时，在仅有常规机组进行调频控制下，频率跌落最低点为49.4 Hz。考虑本文所提可变减载调频策略后，光伏发电能够有效利用减载备用容量，随着系统频率变化而动态调整，提高了频率恢复响应特性。当初始减载率分别为5%和10%时，频率跌落最低点分别为49.5 Hz和49.65 Hz。由此可以看出，初始减载水平越大，在暂态过程中可增发的调频容量也越大，参与系统调频的能力就越强。然而，由于过大的减载水平会使得光伏阵列的工作效率下降，造成正常运行情况下的功率损失，因此采用光伏单独调频受到减载容量的限制，调频效果仍不理想。

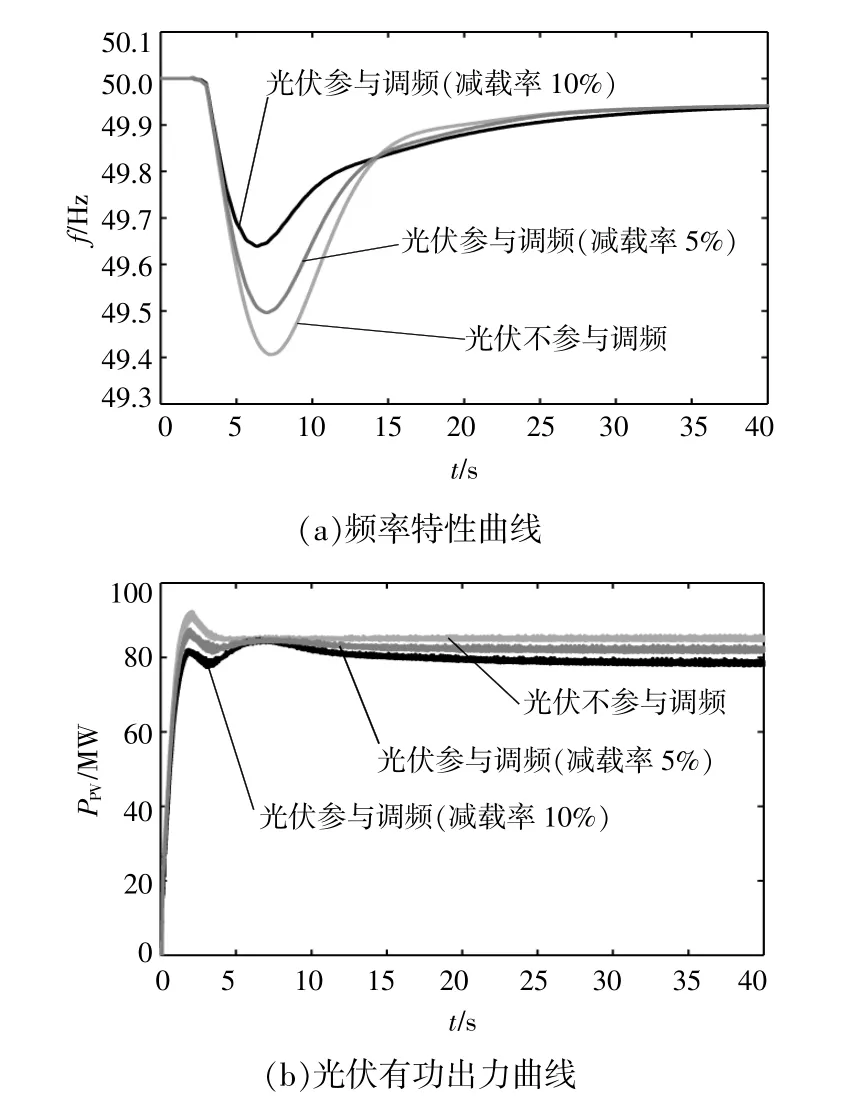
图13 光伏可变减载策略下的特性曲线Fig.13 The characteristic curves of PV power reserve control

4.2 储能自适应调频控制策略验证

将容量为4.5 MW的储能等值电源接入Bus8母线，仿真对比阶跃负荷扰动下的下垂控制定K法和变K法（本文方法）的调频特性。3 s时增投12 MW的负荷，分别考察初始SOC为60%和30%两种情况。

从图14可见，当SOC初始值较高（即电池能量充足时），定K法效果与K的取值相关，K值越大，最大频率偏差越小，调频效果越好，但电池能量下降越快。通过适当选取K值，可以实现调频效果和荷电状态与变K法相当。图14显示，在K=9时定K法与变K法的调频效果及SOC相当。

图14 初始SOC=60%时的调频特性Fig.14 Frequency modulation characteristics when initial SOC=60%

选取定K法（K=9）和变K法进行对比（图15）。由图15可以看出，当初始SOC=30%，即电量较低时，为兼顾SOC的维持效果，下垂控制的出力减小，定K法的最大频率偏差为0.18 Hz，变K法为0.2 Hz。变K法调频效果稍弱于定K法。但由于定K法没有考虑储能SOC的影响，SOC变化曲线下降迅速，很容易达到储能的容量限值而提前退出调频，从而导致频率的二次跌落。

图15 初始SOC=30%时的调频特性Fig.15 Frequency modulation characteristics when initial SOC=30%

进一步地仿真比较储能不参与调频、下垂控制（定K法）、下垂控制（变K法）、变K法加定惯性和本文提出策略等5种情况的效果。从图16和表1可以看出，本文所采用策略的最大频率偏差最小，为0.27 Hz，且在频率初始跌落阶段利用正虚拟惯性，初始频率变化率得到有效减缓，为-0.03 Hz/s。在频率恢复后提供负虚拟惯性支撑，频率恢复速度先增加后减缓，在加快频率恢复的同时兼顾了储能荷电状态的保持，显示了本文提出策略的优越性。

图16 不同调频方式下的频率变化曲线图Fig.16 Frequency change curves under different frequency regulation modes

表1 储能调频策略对比Table 1 Comparison of energy storage frequency modulation strategies

4.3 光储联合调频控制策略验证

在图11仿真系统中，将4.5 MW储能与光伏并联，经变压器接入Bus8母线。在光伏出力分别为60，90 MW时（占比为19.05%和28.57%），加入16 MW的负荷扰动，仿真并验证光伏不参与调频、仅储能参与调频、仅光伏参与调频和本文策略（光储联合参与调频）的频率特性（图17、图18）。

图17 光伏出力占比19.05%时的特性曲线Fig.17 Characteristic curves under 19.05% PV power generation ratio

图18 光伏出力占比28.57%时的特性曲线Fig.18 Characteristic curves under 28.57% PV power generation ratio

通过图17，18可以看出，仅常规发电机参与调频，在光伏出力占比为19.05%情况下，频率最低点为49.45 Hz；在光伏出力占比为28.57%情况下，频率最低点为49.42 Hz。由此可见，光伏占比越大，频率跌落越严重。当系统加入光伏调频时，调频效果明显变好，但由于光伏减载备用有限，调频效果受总备用容量限制。在仅储能参与调频方式下，储能可积极响应频率变化。当光伏出力占比为19.05%时，储能峰值功率占光伏电站的13%，频率最低点比不加控制时提升51%；当光伏出力占比为28.57%时，储能峰值功率占光伏电站的9.2%，频率最低点比不加控制时提升54%。

当采用本文策略时，在综合利用光伏的可变减载调频和储能的自适应调节策略后，在光伏出力占比为19.05%情况下，频率最低点为49.81 Hz；在光伏出力占比为28.57%情况下，频率最低点为49.83 Hz，电力系统的频率稳定性大大提升。结合图17，18可以看出，一次调频过程既充分利用了光伏的减载备用容量，储能调频的出力又没有明显的尖峰特性，有利于储能的荷电状态保持。从图17（c）可以看出，当频率最低点恢复到接近稳定值49.8 Hz时，需要配置的储能容量占光伏电站的10%；从图18（c）可以看出，需要的储能容量为光伏电站的6.7%。采用光储联合控制后比储能单独调节的容量分别减少了3.0%和2.5%。综上所述，本文所提出策略在尽量减少储能配置容量的同时，又取得光储联合调频的较好效果。

5 结论

在新能源高比例接入的背景下，系统的频率稳定性须要以更多的调频手段来支撑。本文在分析并改进光伏、电池储能独立调频策略的基础上，利用储能支撑光伏参与电网一次调频，并进行了仿真比对验证。

①本文所提出的光伏可变减载调频控制策略，控制方式简单，能够跟随频率偏差和光伏最大有功出力变化动态改变光伏的减载率，从而参与系统调频，解决了传统控制策略灵活性差的问题。

②在储能控制策略中，基于Logistic函数的下垂控制，利用SOC分区自适应调节下垂系数，在充放电区间内各设置一个函数，避免了分段函数的复杂性。正、负虚拟惯性控制利用频率偏差变化函数作为调节因子，结合频率变化率及SOC变化特点进行设置。三者的协调运行，既保证了储能的荷电状态，又发挥了储能一次调频的优势。

③利用储能在初始频率跌落阶段为电网提供惯性支撑，并与光伏联合进行一次调频，既有效利用了光伏的减载备用容量，又减少了储能的配置容量，系统的频率稳定性大大地提升。在光伏出力占比为19.05%和28.57%的情况下，储能容量可分别减少3%和2.5%。

本文所提出的光伏和储能调频策略，仅在确定的配置容量下给出了控制效果的验证和比较。对于光伏参与控制的代价、储能投资和参与控制的效益、满足多种场景下的系统频率稳定性要求的协调规划及优化运行等综合考量，均须进一步地深化研究。