基于线性自抗扰的微电网无功控制

朱一昕，钱新，王靖芸，宗晨曦，宗瑜

（江南大学物联网工程学院教育部轻工重点实验室，江苏无锡 214122）

0 引言

光伏、风力等可再生能源以分布式发电（DG）的形式组成微电网[1]。微电网与大电网通过公共耦合点（Point of Common Coupling，PCC）相连接。微电网工作模式分为并网模式和孤岛模式。

传统下垂控制通过计算有功功率和无功功率，分别调节各DG单元的频率和电压，但在低压微电网中，会导致无功功率难以均分[3]～[5]，使逆变器之间产生环流，降低了微电网系统的运行效率。文献[4]，[5]通过改进下垂控制方程，实现了电压自适应调节，降低线路阻抗影响，一定程度地调节了系统无功功率，但是确定合适的虚拟阻抗数值较为困难。文献[6]，[7]通过线路阻抗辨识来获取位置线路的准确阻抗参数，但是辨识出现故障则会影响系统运行。文献[8]利用相对增益矩阵分析了下垂控制中的耦合影响，改善了传统下垂控制在低压微电网中的应用，但是没有考虑无功环流的问题。目前，微电网多采用中央处理器均分无功功率。各DG单元将数据传输至中央处理器，并依据中央处理器发出的控制信息进行动作，然而此双向通信方法极度依赖中央处理器。文献[11]～[15]考虑了刚性负荷和柔性负荷的优化调度，应用分布式控制使DG单元摆脱了对于中央处理器的依赖。并且，当网络采用稀疏通信后，不须要所有节点之间建设通信线路，大大增加了网络的可靠性。文献[16]证明了在任意时刻，只要系统中至少包含一颗生成树，则网络可以进行一致性控制[1]。文献[17]利用电压-相角下垂控制来减少线路阻抗对于下垂控制中功率分配的影响，但是没有对其中所需要的相角下垂系数做明确的说明。

现阶段，下垂控制的改进方法受限于系统或者线路阻抗参数，无法实现准确的无功均分。本文基于LADRC改进的一致性控制策略解决无功均分问题，由于本文所提策略采用稀疏通信网络，可靠性高，降低了DG单元对于通信网络的依赖，保留即插即用的特性，避免了积分反馈的副作用。最后，通过仿真和实验验证了该策略的有效性。

1 图论和一致性算法概述

1.1 图论

在图论中，令G=（V，E）表示图的网络拓扑，V代表图网络中的顶点集；E代表图网络中通信线路，是一个无序的二元组集合，{vi，vj}∈E代表节点i，j之间存在着通信连接。

在有向图中，以入度和出度来分别代表指向顶点的数目和离开的顶点的数目，典型的无向图如图1所示。

图1 无向图示意图Fig.1 Schematic diagram of undirected graph

在无向图中，没有通信链接的方向，因此仅以顶点i关联的边数作为该顶点的度，即di=|Ni|，也可表示为deg（vi）。因此度矩阵被定义为n×n的矩阵D，其元素dij为

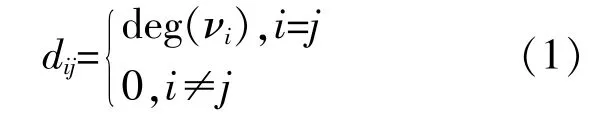
邻接矩阵A表示顶点之间相邻关系的矩阵，在无向图中，A为一个对称的n阶方阵，且主对角线为0。若图中边满足双向且等权重的话，则A中的元素aij为

1.2 一致性算法

在一致性算法中，各个节点在有生成树的情况下，与对应邻居节点进行通信，则所有节点可以达到某个程度的统一。令xi代表顶点i的状态，则最终的状态为

基于无功功率均分的一致性算法为

对应的矩阵形式为

当电力元件之间可以进行数据交互时，其对应的一致性算法的一阶离散形式为

式中：Ln为图G的n×n阶的拉普拉斯矩阵，表示图网络中的混乱程度，定义为L=D-A。

上式的控制算法表示为平均一致性控制算法，同时文献[7]给出了平均一致性算法在数学表示上的典型形式，在满足网络中至少包含一颗生成树的条件下，其网络内的全部节点得状态可以趋于一致，数值上等于系统内该状态量的平均值。

2 线性自抗扰控制

自抗扰控制采用了观测模型总扰动和补偿的方法。本文采用的LADRC可以简化参数设计，控制器主要由跟踪微分器（TD）、线性扩张状态观测器（LESO）和线性状态误差反馈控制率（LSEF）组成，如图2所示。

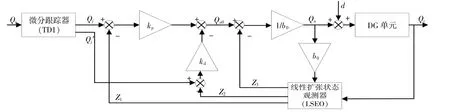
图2 LADRC输入预估法的方框图Fig.2 Block diagram of predictive input method for LADRC

图中：TD根据设定值安排“过渡过程”，作为控制器的输入；LESO根据被控对象的输出和输入信号估计出被控对象的状态量和其总扰动数值；最后利用LSEF决定纯积分器串联型对象的控制率，并补偿由LESO部分估计出的扰动值作为被控对象的最终控制量。

2.1 跟踪微分器

为了处理输入信号，并且避免跟踪信号而产生的高频振荡，可以采取“过渡”过程，使其可以快速无超调的产生输入信号的跟踪信号r1及其微分信号r2。本文采取二阶最速控制综合函数作为系统的“过渡”过程，其离散形式为

式中：h为步长；fhan为最速控制综合函数；x1为输入信号，x2为输入信号的微分信号；h0为滤波因子，h0取值2×10-5，若其值大于h，可消除跟踪输入信号产生的噪声放大现象；r为跟踪因子，r取值1×1040。

2.2 线性扩张状态观测器

为了消除系统中扰动，本文以状态观测器为基础，将影响被控对象的扰动扩张成新的状态变量，构成新的观测器，即扩张状态观测器。

状态观测器由被控对象的控制量和被控对象的输出量构成，不须要被控对象的精确数学模型。基于“最短路径”的设计思想，本文控制器设计为二阶，其扩张状态为被控对象的内扰与外扰之和，为第三阶。扩张状态观测器为

式中：β01，β02，β03为线性状态观测器增益；文中采用的LESO参数3ω0，3ω02，ω03，ω0可以依据实际情况取高值，本文的ω0选取50 000；e（k）为状态观测器观测值和实际值的误差；Z1，Z2，Z3为被控对象的各阶状态量，状态观测器通过控制信号和被控对象的输出值来观测出被控对象的各阶状态量。

2.3 状态误差反馈控制率

为了简化传统自抗扰过程中参数整定问题，LADRC的控制分量u0为被控对象的一阶和二阶误差的简易线性组合，LADRC通过扰动估计值Z3（k）的补偿来生成最终的控制量u，其状态误差反馈控制率为

式中：e1，e2分别为过渡过程和扩张状态观测器输出之间的差值；z3为观测器观测出的系统的总扰动；kp，kd为控制器增益，分别为ωc2和2ζωc；b0为系统的补偿因子；本文ωc为400，ζ为0.5，b0为5×1012。

2.4 基于线性自抗扰优化的控制策略

本文在一致性理论基础上，采用线性自抗扰优化PID部分，使各DG单元均分网内的无功功率。本文控制结构类似微电网的分层控制，但不采用中央控制器，因此减少了DG单元对于通信的依赖，其控制策略如图3所示。

图3 一致性控制策略框图Fig.3 Block diagram of consistency control strategy

图中，DG单元底层采用了“下垂控制+电压电流双闭环”的控制方式，由功率控制环计算DG单元的有功无功数值，作为后续电压环的控制输入。电流环根据电压控制环输出的参考电流值，输出逆变器所需要的调制波形。当采用传统的下垂控制方法对DG单元进行控制时，DG单元间要保证各自参考频率、参考电压、出口电压和等效输出阻抗相等，才能使得微电网内部各个DG单元之间有功和无功实现准确的均分。在低压微电网中，线路阻抗多呈现为阻性或者阻感性，且各个DG单元到母线之间的距离不等，导致DG单元之间难以实现准确的无功均分。本文在一致性理论的基础上，引入了虚拟阻抗和线性自抗扰控制，可以改善系统线路阻抗比，提高系统的运行稳定性，并且通过稀疏网络通信，使得网内DG单元精确的按照各自容量输出无功功率，减少网内的无功环流。传统的一致性算法对于系统所需的补偿量多采用基于误差补偿的PID控制形式。本文采用LADRC改进PID控制部分，其补偿量经过负反馈输入到Q-V控制环节中。

4 仿真分析

4.1 仿真算例

为了验证所提控制策略的有效性，搭建了微电网仿真系统。该系统包括3个DG单元，各个DG单元之间结构和通讯关系如图4所示。

图4 仿真模型及其通讯结构Fig.4 Simulation model and communication structure

本文的仿真算例采用单向通信，每个DG单元仅须要将自身的信息传输给相邻的一个单元，并不须要对网内其他所有单元进行数据传输。由此可以明显看出，与传统的基于中央处理器的控制方式相比，该控制方式所需要的通信量大为减少。

4.2 算例分析

为了验证所提方案的有效性，将传统一致性策略与所提控制策略进行比较，研究两种不同策略在负载改变下的运行情况。仿真中DG单元的下垂系数mi=5×10-6V/Var，ni=1×10-4Hz/W。各个负载的功率如表1所示，线路阻抗如表2所示。其中：线路阻抗1、线路阻抗3和线路阻抗4分别对应DG1，DG2和DG3到母线处的等效线路阻抗；线路阻抗2为输电线路上的等效阻抗。

表1 负载参数Table Load parameter

表2 线路阻抗参数Table 2 Line impedance parameters

仿真有3台容量相同的DG单元和3个负载，负载突变时的功率均分情况如图5所示。

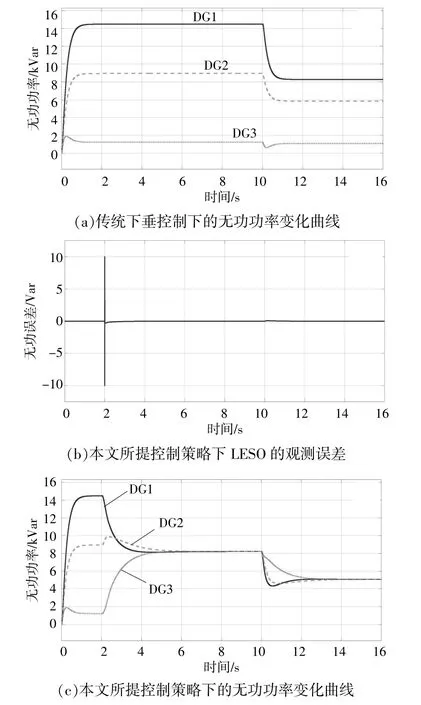
图5 不同控制策略下微电网的运行情况Fig.5 Operation of microgrid under different control strategies

微电网在2 s时采取一致性控制策略，10 s时负载1脱离微电网，网内总体无功功率由25 kVar降到15 kVar。可以看出，在采用一致性算法后，微电网可以实现准确的无功功率均分，并且基于状态估计补偿的LADRC即使没有积分环节也能对DG单元进行无静差调节，其LESO部分的观测误差虽然在负载切换时有所波动，但最终可以实现准确的观测。

为了更进一步的验证所提控制策略的有效性，在所搭建的实验平台上进行实验验证。DG模块的出口滤波电感Lf=1.5 mH，滤波电容Cf=300 μF，其采样周期为10 ms。各DG单元下垂系数和线路阻抗同表1，2。仿真波形如图6所示。

图6 2种控制策略下微电网内运行情况Fig.6 The operation in the micro grid under two control strategies

图6中，I1，I2和I3分别对应着DG1，DG2和DG3的A相电流。可以看出，由于线路阻抗不匹配的原因，传统下垂控制中，各DG单元不能均分网内无功功率，造成电流相位有所偏移，而采取本文所提的控制策略后，DG单元可以实现网内的无功功率均分。

5 结论

本文针对孤岛模式下微电网内的无功功率均分问题，提出了一种基于LADRC改进的一致性控制策略来改善同等容量DG间的无功出力分配。该策略可以不用测量线路阻抗的准确的参数，通过一致性算法协调各DG单元之间的无功分配情况，使得网内的无功功率可以按照各自DG单元的容量进行分配。文章用LADRC改进了传统的一致性控制策略上，可以看出，LADRC能够对DG单元实现准确的状态估计并实时补偿，避免了积分饱和现象的产生。最后通过仿真和实验验证了所提控制策略的有效性。相较于传统的基于中央处理器的控制方式，本文所采用的分布式通讯增强了系统的鲁棒性。