基于二次谐波环流注入方法的混合MMC电容电压平衡控制策略

曹鑫巍，任文明，王炜信

（中国航空综合技术研究所，北京 100028）

0 引言

自模块化多电平变换器（MMC）的拓扑结构被提出以来，在高压直流输电系统中得到广泛应用［1-5］。与基于半控型器件的电网换相变换器相比，MMC 具有更加优越的模块化特性、可靠性、电能输出质量以及可延展性等［6］。基于半桥子模块（HBSM）的MMC（HBSM-MMC）结构最为简单，成本低，运行效率高，但是不具备直流故障隔离与穿越能力［7-9］。学术界提出了多种具备直流故障处理能力的子模块拓扑［10-13］，基于全桥子模块（FBSM）的MMC（FBSM-MMC）结构因具有拓扑结构更加简单、输出电平数较多等特点，获得广泛应用与推广［12］。但相较于HBSM-MMC，FBSM-MMC 需要更多的开关器件，从而带来了更高的导通损耗与系统成本。

为了同时兼顾MMC 的较高运行效率与直流侧故障处理能力，通过将HBSM-MMC 各桥臂中的部分HBSM 用FBSM 替代，得到了基于HBSM 与FBSM 的混合MMC［14-16］。在高压直流输电系统中，当出现恶劣的天气或系统绝缘设备故障等异常情况时，需要降低直流电压以保证高压直流输电系统的可靠运行，混合MMC 将在过调制状态（交流侧相电压幅值高于直流侧电压的一半）下持续传输有功功率，交流电网电压保持不变，直流侧电流保持不变。当直流电压降低超过一定范围时，混合MMC 中2 种子模块的电容电压将无法保持平衡，其中一种子模块电容由于过度充电，电压不断升高，另一种子模块电容由于过度放电，电压不断降低，最终混合MMC 将因电容故障触发保护系统而停运［14］。

为了抑制混合MMC 过调制运行中电容电压不平衡现象的发生，已有的解决方法包括减小功率因数［14］、增加FBSM 数量的比例与基频无功环流注入［17］以及二次谐波环流注入［18-19］等。文献［14］分析了直流侧电压严重降低时子模块电容电压的不平衡现象，并通过降低混合MMC 运行的功率因数抑制了电容电压不平衡的发生。文献［17］分析了子模块混合比、运行功率因数以及电压调制比对子模块电容电压平衡的影响，得出以下结论：电压调制比越大，子模块电容电压越容易产生不平衡；功率因数越小，子模块混合比越大，子模块电容电压越容易实现平衡。同时通过基频无功环流注入的方法，实现了直流电压降低时子模块电容电压平衡的控制，但是基频环流的注入会增大子模块开关管的电流应力，显著增加混合MMC 的导通损耗。相比之下，文献［18］提出基于二次谐波环流注入实现子模块电容电压平衡的控制方法，能够有效降低对开关管的电流应力要求，但是其获得二次谐波环流参考幅值的过程需要大量傅里叶分析，计算方法复杂，实施困难。文献［19］提出了一种简化的二次谐波环流参考幅值生成方法，减小了在线运算量，但所提计算方法所适用的过调制范围有限。综上所述，二次谐波环流注入方法能够获得更加优越的系统运行效果，实现的关键在于通过高效的计算方法获得有效可靠的二次谐波电流参考幅值。

本文提出一种简化的二次谐波参考幅值计算方法。根据混合MMC 过调制下的子模块电容电压波动特点，提出实现子模块电容电压平衡的充分条件，据此计算满足电压平衡条件的二次谐波环流参考幅值。通过仿真与实验分别进行验证，证明了本文所提二次谐波注入法可实现子模块电容电压平衡。

1 混合MMC超调运行

1.1 混合MMC超调运行机理

混合MMC 的拓扑结构如图1 所示，上、下桥臂中均包含N个子模块（NHB个HBSM 与NFB个FBSM）与1 个桥臂电感Larm。图中，Udc、Idc分别为直流侧电压、电流；usx（x=a，b，c）为交流侧电网电压；uxo、ixo分别为各相桥臂交流端口电压、电流；ixp、ixn分别为各相上、下桥臂电流；CHC、CFC分别为HBSM 与FBSM 的电容值。由于本文重点关注HBSM 与FBSM 之间电容电压平衡，可以假设各HBSM 中的电容电压uHC相同，各FBSM中的电容电压uFC相同。

图1 混合MMC拓扑结构Fig.1 Topology structure of hybrid MMC

定义混合MMC的调制比m为：

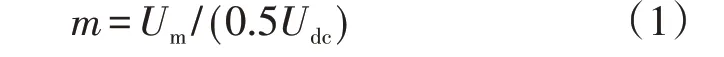
式中：Um为交流侧的相电压幅值。当m>1 时，系统运行在过调制状态，交流侧电压的升高与直流侧电压的降低都会引起混合MMC 的超调运行。定义混合比h为FBSM 数量占子模块总数的比值，其表达式为：

在高压直流输电系统中，h一般取1/2，该混合比既满足了直流侧短路故障穿越的需求，也满足了系统设计的经济性要求。混合MMC 既可运行于受端逆变状态，又可运行于送端整流状态，其运行互为逆过程，本文中只针对逆变状态下的混合MMC 进行分析，整流状态下的分析依此类推。同时，由于直流侧电压的降低对三相桥臂子模块的影响效果相同，且对同相中的上下桥臂影响对称，本文以a 相上桥臂为例，对直流电压降低下的混合MMC 运行特性进行分析。在混合MMC 中，假设环流中只含有直流分量，根据基尔霍夫电压、电流定律，桥臂电压与桥臂电流可以表示为：

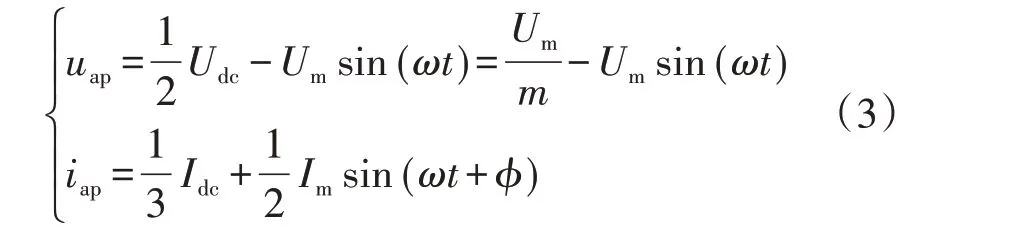
式中：uap为a 相上桥臂的桥臂电压；Im为交流侧的相电流幅值；φ为功率因数角；ω为系统角频率。

图2 为直流侧电压降低时混合MMC 的桥臂电压与电流波形，图中uapN、iapN分别为直流侧电压正常情况下的桥臂电压、电流。当直流侧电压降低时，根据式（3），桥臂电压中的交流分量不变，直流分量向下平移后，桥臂电压uap出现负值；直流电流Idc不变，有功功率减小，由于交流电压保持不变，交流电流幅值减小，与直流电压正常情况下的桥臂电流相比，电压降低时桥臂电流iap中的负值部分面积减小甚至消失。

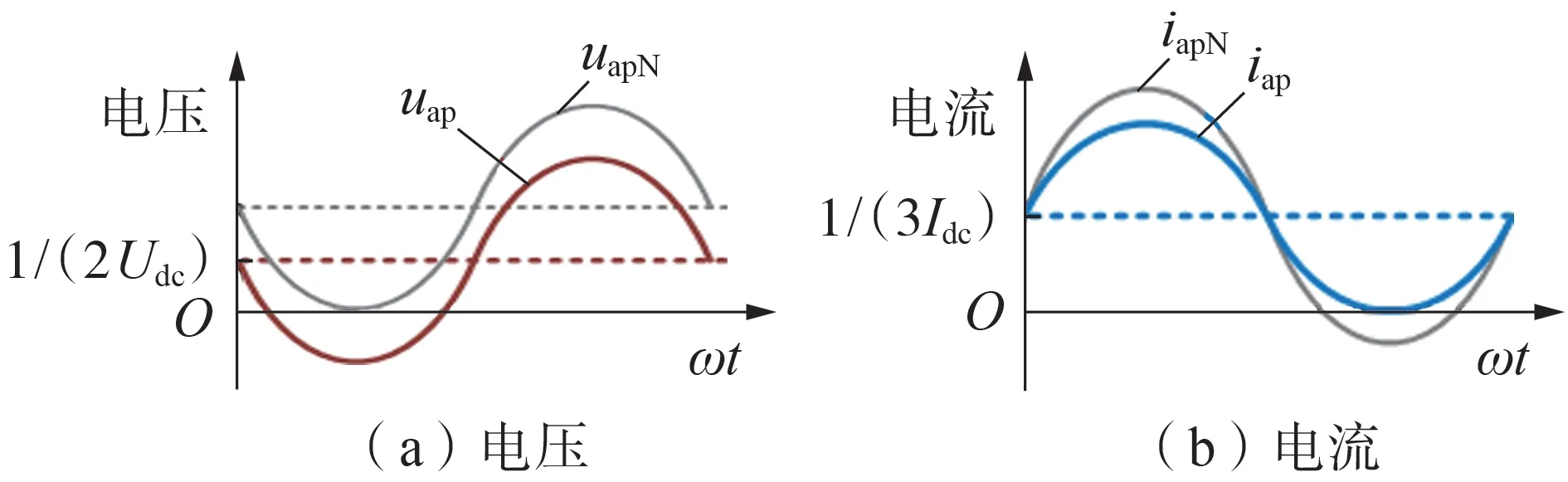
图2 直流侧电压降低时的桥臂电压与电流Fig.2 Arm voltage and current when DC voltage decreases

过调制运行下，混合MMC 子模块投入原则如下：①当桥臂参考电压为负时，仅FBSM 通过输出负电平实现桥臂参考电压值输出，根据电容电压排序结果选取FBSM 投入，此时，FBSM 电容放电，HBSM电容电压保持不变；②当桥臂参考电压为非负时，HBSM 与FBSM 的电容同时参加排序，根据排序结果与电流方向选择子模块投入或旁路［17］，此时FBSM等效为HBSM。

1.2 电容电压不平衡机理

图3 为2 种不同调制比下（m=1.55 与m=1.8）子模块电容电压示意图。图中，uFm为所有FBSM 可输出的最大正电压；θ1—θ7为一个完整的基频周期，θ1与θ2为桥臂电压的过零点，θ4与θ5为桥臂电流的过零点，θ3与θ6为桥臂电压与uFm的交点相位；θb为HBSM电容电压与FBSM 电容电压的平衡点，当HBSM 与FBSM电容电压能够实现平衡时，在不同程度的直流侧电压降低下，θb可以位于［θ1，θ7］之间任意时间段内。图3（a）为θb存在于（θ6，θ7］之间的子模块电容电压实现平衡时的电压波形。当HBSM 与FBSM 电容电压不能满足平衡条件时，θb将不存在，图3（b）为电容电压不平衡时的电压波形。

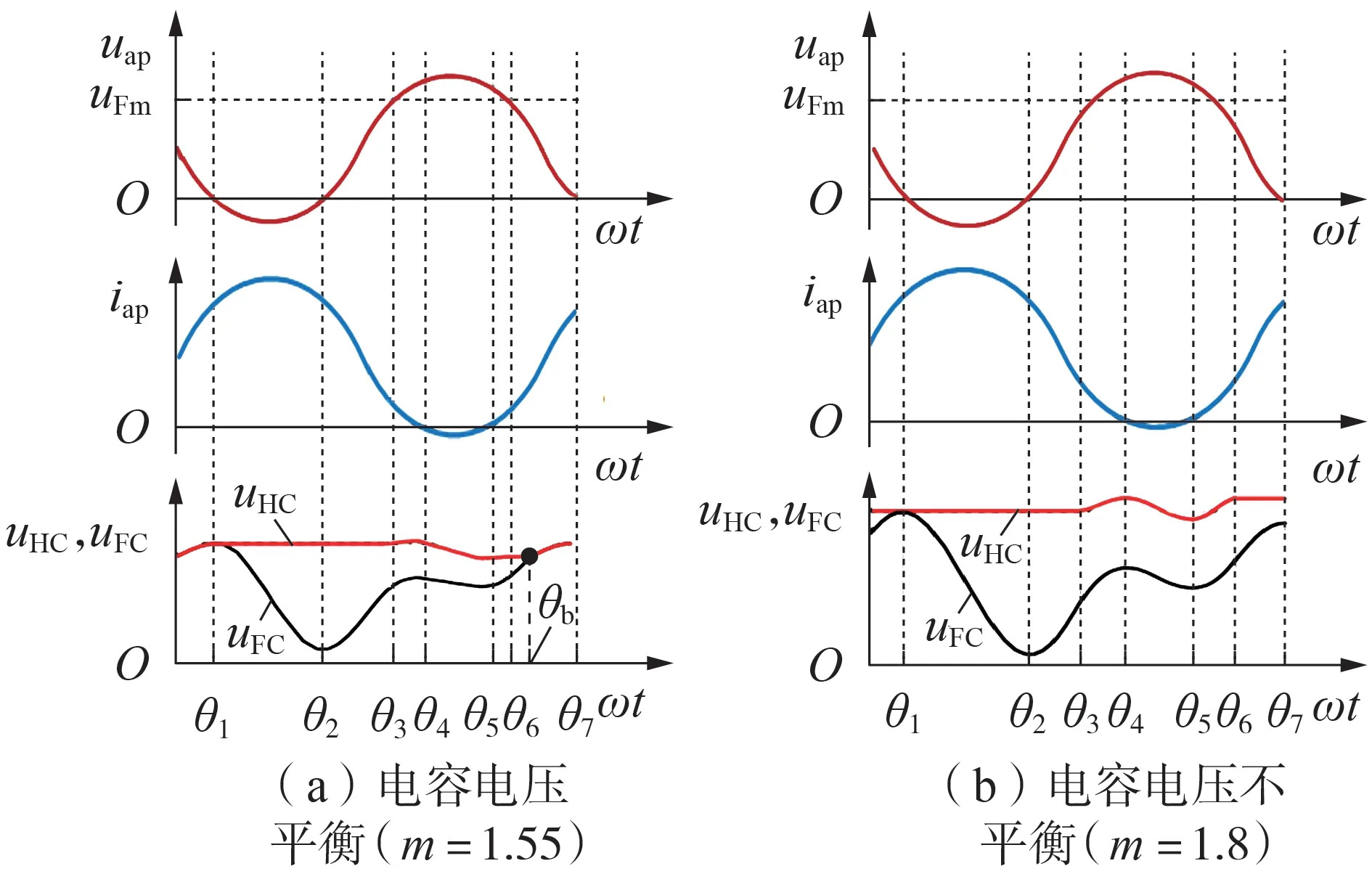
图3 2种过调制下的子模块电容电压Fig.3 Capacitor voltage of submodule under two kinds of over-modulation states

在图3（a）中，假设桥臂中某一时刻同时投入的子模块数为nap：①在［θ1，θ2］内，选择电容电压较高的nap个FBSM 以负电平投入，电容电压降低，此时，由于被旁路的HBSM 电容电压保持不变，2种子模块电容电压之间的电压差增大；②在（θ2，θ3］内，FBSM 由于电容电压较低将被优先投入，选择电容电压较低的nap个FBSM 输出正电压，使电容电压充电，此时，HBSM 电容电压依然保持不变；③在（θ3，θ4］内，由于桥臂参考电压uap超过uFm，NFB个FBSM 全部投入，nap-NFB个HBSM 补充投入，所有投入的子模块都被充电，因此，HBSM 与FBSM 电容电压均增大；④在（θ4，θ5］内，桥臂电流为负，由于HBSM 电容电压较高，因此，HBSM 优先投入，输出正电平使电容放电，此时，NHB个HBSM 全部投入，nap-NHB个FBSM 补充投入；⑤在（θ5，θ6］内，uap>uFm，FBSM 电容电压低于HBSM，NFB个FBSM 全部投入，nap-NFB个HBSM 补充投入；⑥在（θ6，θb］内，nap个FBSM 将被优先投入充电，电压升高，HBSM 电容电压不变，在θb处FBSM 与HBSM 电容电压相等；⑦在（θb，θ7］内，HBSM 与FBSM将获得均等的投入机会，2 种子模块的电容电压相互重叠，保持相等。

图3（b）中，混合MMC 调制比增大为1.8，此时桥臂电流的负值部分进一步减小。由于HBSM 只具备非负电平输出能力，其在一个周期内的放电机会与放电能量大小将进一步减小，此时，HBSM 的电容在一个基频周期内的能量变化将大于0，充电能量大于放电能量。当一个基频周期结束之后，HBSM 电容由于充电过多，电容能量增大，电压增大；而FBSM电容由于放电过多，电容能量减小，电压减小。随着周期数的增加，2 种子模块之间的电压差将不断累积，最终造成系统故障，被迫停运。因此，混合MMC在过调制下的电容电压不平衡，是由调制比增大导致桥臂电流负值部分减小所引起的。

因此，如果能够保证HBSM和FBSM电容在一个周期内的能量变化为0，即可实现电容电压的平衡。式（4）为混合MMC 过调制下HBSM 与FBSM 电容电压平衡的充分必要条件。

式中：ΔEHB、ΔEFB分别为HBSM、FBSM 电容在一个周期内的能量变化平均值。

2 二次谐波环流注入实现电容电压平衡

通过二次谐波环流注入实现电容电压不平衡抑制的方法，其有效性已经在文献［18-19］中得到验证。图4 为m=1.8 时注入二次谐波环流后电容电压波形。图中，iap0为二次谐波环流注入前的桥臂电流；i2ca为注入的二次谐波环流。由图可知当注入合适的二次谐波环流时，能够削减（θ1，θ2］之间桥臂电流正峰值对FBSM 电容的放电，同时增强（θ4，θ5］之间桥臂电流负峰值对HBSM 电容的放电，从而使uHC与uFC能够在每个基频周期内出现平衡点θb，实现HBSM与FBSM电容电压之间的平衡。

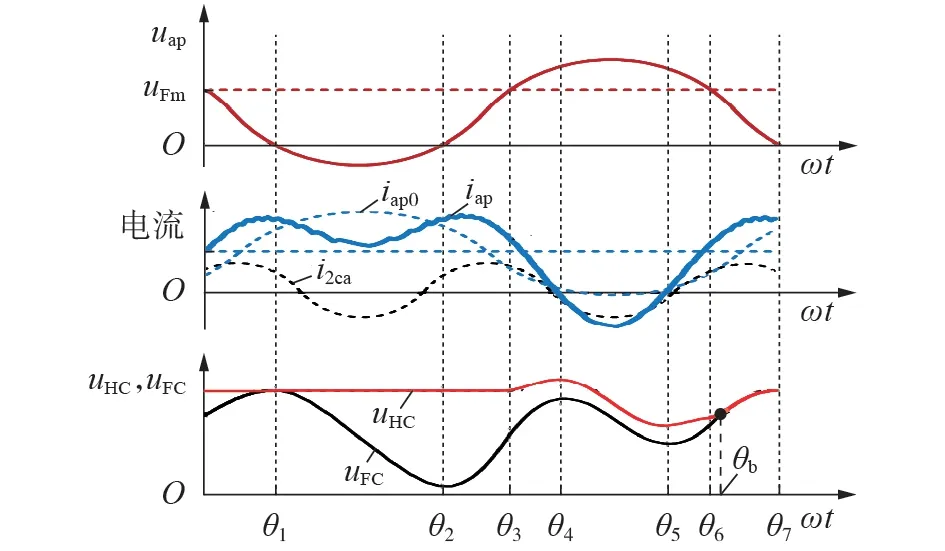
图4 m=1.8时二次谐波环流注入后电容电压波形Fig.4 Waveform of capacitor voltage after second-order harmonic circulation injection when m=1.8

文献［16］中已经证明，设计所注入的二次谐波环流相位，当二次谐波环流如式（5）所示时HBSM 电容可获得最佳的能量补偿效果。

2.1 二次谐波环流参考幅值的生成

在混合MMC 中，每个桥臂在一个周期内的电容能量变化为0，即HBSM 电容能量与FBSM 电容能量的变化之和互为相反数，因此，式（4）所示的电容电压平衡条件中，仅需要保证ΔEHB或ΔEFB中的一个为0，另一个也会自动为0［17-18］。本文控制ΔEHB=0，注入二次谐波环流之后，HBSM 电容在一个周期内的能量变化为：

式中：ΔEHB（i，j）为所有HBSM 电容在（θi，θj］之间的总能量变化，i，j=1，2，…，7；uHB（i，j）为所有HBSM 电容在（θi，θj］之间承担的总电压；uC为子模块额定电压。桥臂电压与uFm的交点相位θ3与θ6分别为：

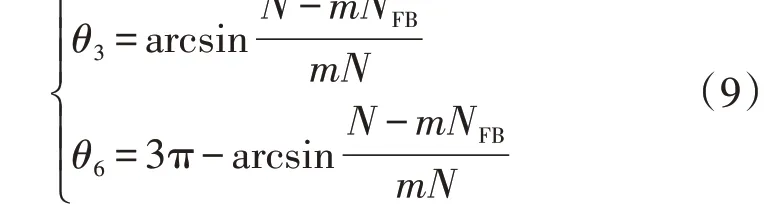
由于注入二次谐波环流后的桥臂电流过零点θ4、θ5的坐标求解十分复杂，需要对式（8）进行简化。由图3可知，式（8）中的分段能量为：

由此可以得到二次谐波环流幅值的取值范围为：

对于特定的m，在单位功率因数下能够满足平衡条件所需的二次谐波环流参考幅值，可以满足全功率因数范围内的电容电压平衡需求。

2.2 系统整体运行与控制

附录A 图A1 为混合MMC 整体运行流程图，当直流侧电压正常时，混合MMC 的工作模式与控制策略与HBSM-MMC 一致，HBSM 与FBSM 电容电压保持平衡。当检测到直流电压发生降压运行时，混合MMC 工作于过调制状态。如果降压运行不会导致2种子模块电容电压出现不平衡，则混合MMC 将无需注入二次谐波环流信号；如果降压运行导致2 种子模块电容电压出现不平衡，则注入二次谐波环流的参考幅值通过式（17）获得，参考相位通过桥臂电流相位检测，并产生90°相位差获得。

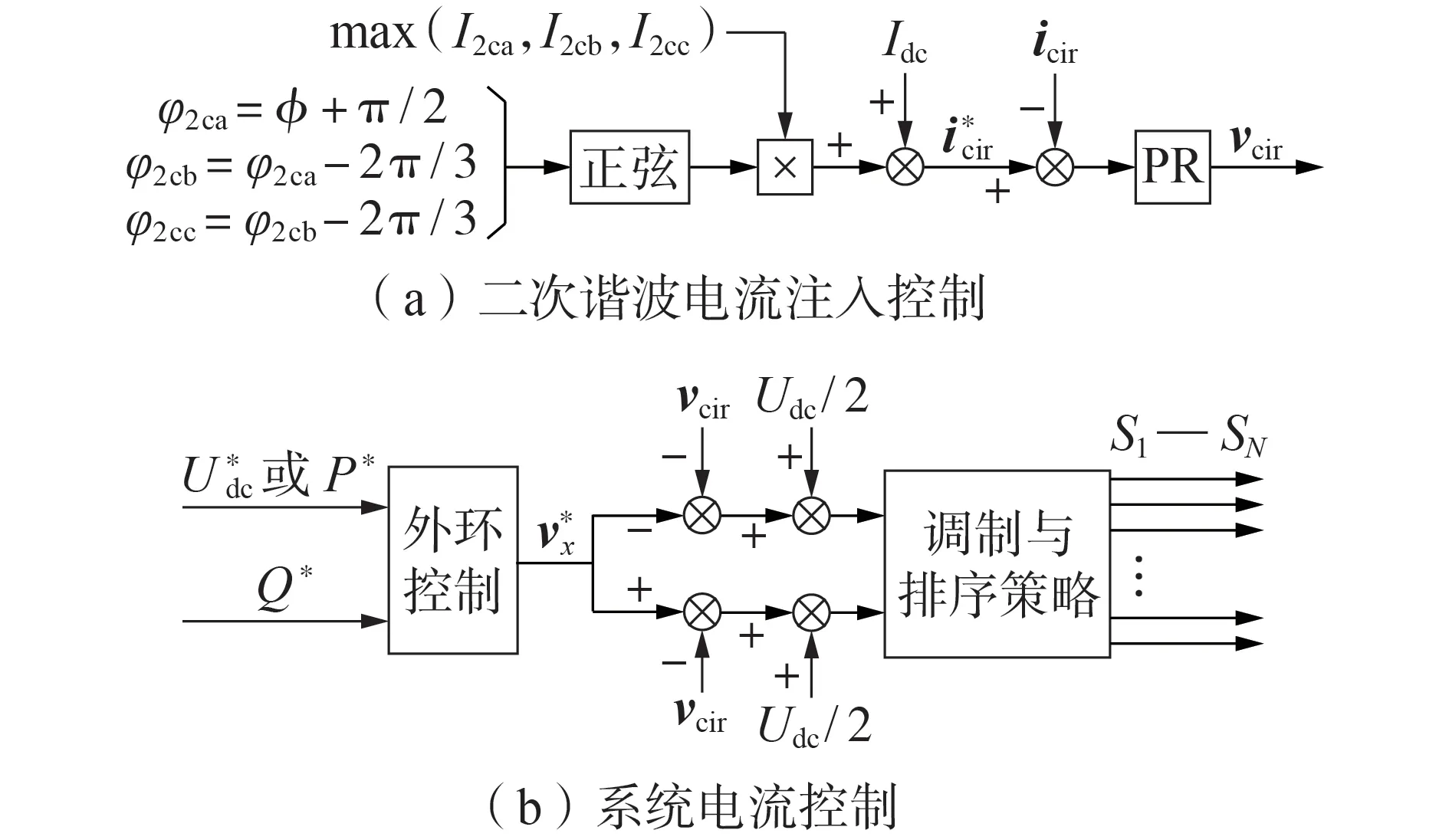
图5 混合MMC系统控制框图Fig.5 Control block diagram of hybrid MMC system

3 仿真与实验验证

3.1 仿真验证

本文在MATLAB／Simulink 平台搭建三相混合MMC 仿真模型，对所提控制策略进行验证，附录A表A1为仿真模型的相关参数。

图6 为直流侧电压降低至一半时，即调制比由m=1 变为m=2 时，混合MMC 子模块电容电压发生不平衡的仿真结果。0.5 s 时，直流侧电压由60 kV 下降为30 kV，无二次谐波环流注入时HBSM 电容电压不断升高，FBSM 电容电压不断降低，子模块电容电压之间发生严重的不平衡。

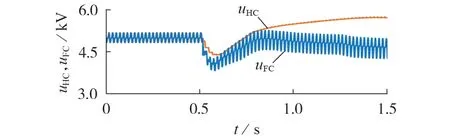
图6 无二次谐波环流注入时的子模块电容电压波形Fig.6 Waveforms of submodule capacitor voltage without second-order harmonic current injection

当直流侧电压降低，调制比m=2时，采用本文所提二次谐波环流注入方法可实现混合MMC 电容电压平衡，仿真结果见附录A 图A2 和图7。图A2 中，直流侧电压在0.5 s时降低至一半，混合MMC运行在超调状态下m=2。直流侧电流大小保持不变，因此有功功率P大小降为额定功率的1/2。交流侧电压保持稳定输出，交流侧电流随着有功功率的降低也减小为额定值的一半。根据式（17）计算得到二次谐波环流参考幅值为100 A，与图A2 所示的0.5 s 时二次谐波环流参考幅值相等。

图7 中，在（0，0.5］s 正常运行下，环流中仅包含直流分量iaz；0.5 s 后，混合MMC 桥臂电流中出现二次谐波环流。在直流侧电压降低之前，HBSM 与FBSM 电容电压完全重合，这是因为此时FBSM 不会输出负电平，2 种子模块运行模式相同；0.5 s 后直流电压降低，通过注入二次谐波环流实现子模块电容电压的平衡，即HBSM 电压满足式（4）所示条件，此时在一个基频周期内存在平衡点θb位于（θ5，θ7］之间。

对比图6与图7中的子模块电容电压波形，可以验证本文提出的简化二次谐波环流注入方法能够有效抑制电容电压的不平衡，平衡后的电容电压均围绕其参考值5000 V波动。

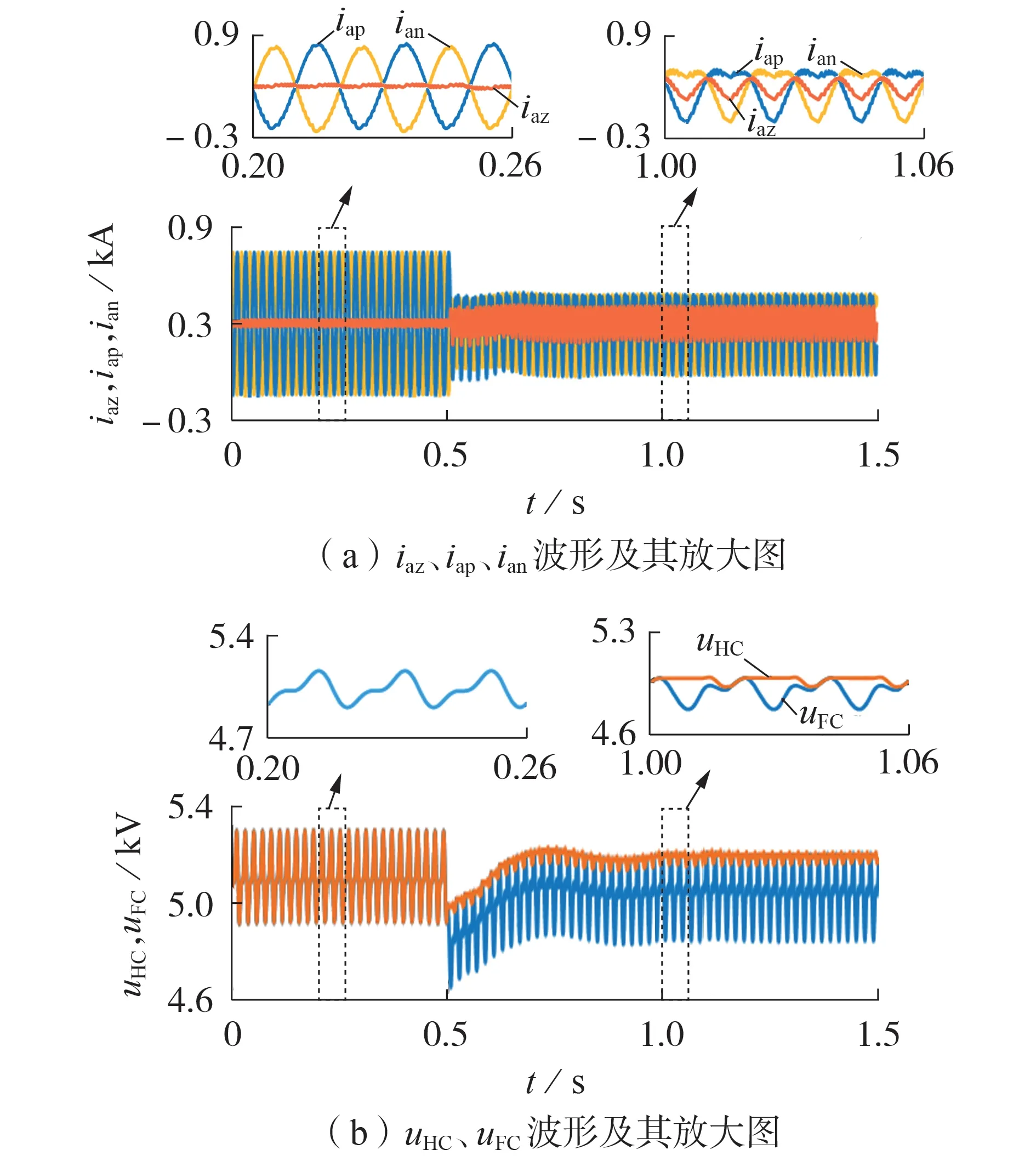
图7 m=2时注入二次谐波电流实现电容电压平衡的仿真波形Fig.7 Simulative waveforms of capacitor voltage balance achieved by second-order harmonic current injection when m=2

3.2 实验验证

本文搭建了单相混合MMC 实验平台验证所提方法与仿真结果的有效性，附录A 表A2为实验平台参数。混合MMC 直流侧电压降低至一半后，子模块电容电压不平衡的实验波形如附录A 图A3所示，可见HBSM 电容电压在调制比m=2 后迅速上升，FBSM电容电压迅速下降。

图8为混合MMC在直流侧电压降低前、后（200 V降低至100 V）的电容电压平衡实验结果，包括直流电压大小、子模块电容电压及环流，其详细波形分别见附录A 图A4、A5。由图8（a）可知：直流侧电压为200 V；HBSM 与FBSM 电容电压完全重合，通过排序算法使二者在整个基频周期内均相等；a相桥臂环流icira中直流分量为2 A，无二次谐波环流。由图8（b）可知，当直流电压降低至100 V 时，在桥臂中注入幅值为1 A 的二次谐波环流，实现电容电压平衡，此时系统功率降低为原功率的75%。由图A5（b）可知，a相桥臂环流icira中出现了二次谐波环流，由于二次谐波环流的注入，其正向峰值减小，负向峰值增大。注入二次谐波环流后，对比图A3所示的电容电压不平衡波形，子模块电容电压最终满足式（4）所示的平衡条件，此时θb位于（θ3，θ4］之间。实验结果验证了本文所提简化二次谐波环流参考幅值计算方法能有效实现HBSM与FBSM电容电压之间的平衡。

图8 m=2时电容电压平衡的实验结果Fig.8 Experimental results of capacitor voltage balance when m=2

4 结论

本文分析了混合MMC 系统在直流电压降低时的工作机理以及2 种子模块电容电压的能量充放电过程，通过对HBSM 电容在一个周期内的能量变换计算，根据实现子模块电容电压平衡的充要条件，得到一种简化的二次谐波环流参考幅值计算方法，使该二次谐波环流的注入能够抑制过调制下的电容电压不平衡。本文所提出的二次谐波环流参考幅值计算方法具备以下创新点与优势：本文的计算基于HBSM 电容的能量变化展开，一方面在计算过程中减小了计算量，简化了对桥臂电流过零点的计算过程；另一方面本文所提二次谐波参考幅值计算方法得到的结果具备一定的裕度，无需再对计算所得的结果进行放大处理。因此，本文所提基于二次谐波环流注入实现电容电压平衡的方法能以较小的计算量获得可靠的二次谐波环流参考幅值，从而实现混合MMC 在过调制运行时的子模块电容电压平衡。本文通过仿真与实验验证了所提方法的有效性。

附录见本刊网络版（http：//www.epae.cn）。