基于通径分析和相似时刻的特高压变压器顶层油温预测
2021-11-20谭风雷何嘉弘
谭风雷,陈 昊,何嘉弘
(1. 国网江苏省电力有限公司检修分公司,江苏 南京 211102;2. 东南大学 电气工程学院,江苏 南京 210096)
0 引言
随着电网建设规模的逐步扩大,电力变压器在投数量逐年增加,其健康水平决定着电网的供电可靠性,特高压变压器的重要性更是不言而喻。特高压变压器的热状态决定着其内部绝缘水平,影响其使用寿命和健康状态。热状态主要是通过热点温度与顶层油温进行衡量[1-4]。目前,热点温度一般是利用顶层油温来间接估算,如果可提前预测顶层油温,则能有效评估热点温度,为特高压变压器内部绝缘状态判断提供理论依据。同时顶层油温的准确预测有助于研究极限顶层油温下的最大负荷,对提高特高压变压器容量利用率具有重要意义[5-9]。
目前,关于热点温度和顶层油温的计算方法,国内外已有大量研究,总体上主要分为经验公式、热路模型和数值计算3类[10-15]。其中,经验公式是利用现有的计算公式和人工经验对热点温度进行粗略估计,一般误差较大;热路模型是基于热电类比法建立温度计算模型,精度受模型参数影响较大;数值计算是通过变压器内部结构和散热介质的研究,建立多物理融合的内部温度分布,进而估算热点温度,结果基本符合变压器的真实热状态。另外,随着人工智能算法在变压器领域应用的不断深入,部分研究者将人工智能算法逐步应用到变压器热点温度和顶层油温的预测中。文献[16]考虑到广义回归神经网络具有容错性高和鲁棒性强的特点,将其应用于变压器热点温度的预测。文献[17]提出了基于支持向量机的变压器热点温度预测方法,利用遗传算法优化相关参数,得到了优化BP神经网络的预测效果。文献[18]提出了基于粒子群优化算法的混合核极限学习机(PSO-HKELM)的变压器顶层油温预测方法,采用核极限学习机对顶层油温进行拟合预测,并基于粒子群优化算法优化混合核函数的相关参数,提高了预测精度。
目前尚未有文献采用相似日法预测热点温度和顶层油温,而相似日法[19-23]在短期预测领域是一种较为简单有效的方法,该方法是从历史样本本身挖掘数据特征,无需研究样本内部潜在关系。基于此,本文借助相似日法的思想,进一步细化到时刻,提出了一种基于通径分析和相似时刻的特高压变压器顶层油温预测方法。首先基于通径分析方法确定特高压变压器顶层油温的主要影响因素;然后基于逼近理想解排序(TOPSIS)法、线性加权原理和简单相关系数得到综合因素相关度;最后结合综合因素相关度,研究顶层油温预测方法的计算步骤,并将其应用到华东地区某特高压变压器顶层油温预测算例中,验证所提方法的有效性。
1 特高压变压器顶层油温的主要影响因素分析
鉴于特高压变压器顶层油温的影响因素较多,有的因素对顶层油温的影响较大,有的因素对顶层油温的影响较小,若考虑全部影响因素,不仅算法复杂、实现困难,而且将影响较小的因素纳入算法不符合数学建模的基本规则,影响算法效果,故需对特高压变压器顶层油温的主要影响因素进行分析。实际上,特高压变压器一般包括主体变压器和调补变压器2 个部分,因此特高压变压器顶层油温也包括主体变压器顶层油温和调补变压器顶层油温2 个部分,考虑到2 种顶层油温的分析预测过程完全一致,为简化分析,下文以主体变压器顶层油温预测为例进行说明。
1.1 通径分析方法
考虑到特高压主体变压器顶层油温的不同影响因素间存在相互作用,本文采用通径分析方法[24]研究不同影响因素间的相互作用。通径分析方法指出,当多个自变量与因变量存在一定相关性时,某个自变量对因变量的影响(称为简单相关系数),不仅表现为该自变量本身对因变量的影响(称为直接通径系数),还体现在该自变量通过其他自变量对因变量的影响(称为间接通径系数)。
假设自变量x1、x2、…、xk、…、xN和因变量y都包括M组样本,利用通径分析方法可得xk与y的直接通径系数R1(k)为:
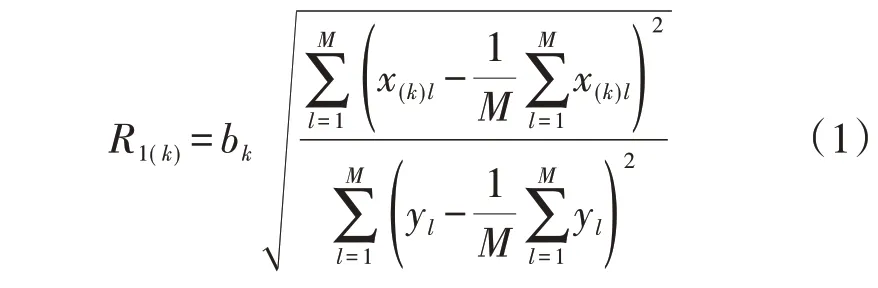
式中:x(k)l为xk的第l个样本值;yl为y的第l个样本值;bk为偏回归系数。
同理可得xk通过xk+1对y的间接通径系数R2k(k+1)如式(2)所示。
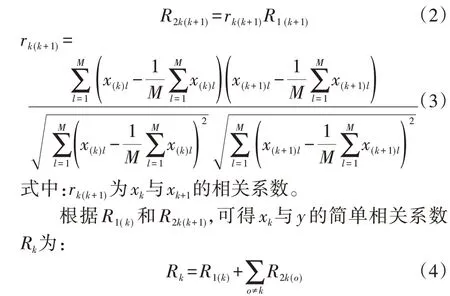
1.2 简单相关系数计算
针对特高压主体变压器顶层油温的多种影响因素,本文将重点研究气象、时间和负荷这3 种影响因素。其中气象因素主要包括环境温度、空气湿度、降雨情况、光照强度、风速等级和环境气压这6 种因素。为便于描述,分别定义MTi(j)、Wij、Sij、Jij、Gij、Fij、Qij、Pij、Tij为待预测日前第i(i=0 表示待预测日)天时刻j的顶层油温、环境温度、空气湿度、降雨情况、光照强度、风速等级、环境气压、负荷因子、时间因子,E为历史样本数量。下面结合通径分析方法给出各影响因素的简单相关系数的计算过程。
1)获取8 种影响因素并进行量化处理。考虑到环境温度、空气湿度、降雨情况、光照强度、风速等级、环境气压以及负荷因子这7 种影响因素可直接获得量化数据,本文重点介绍对时间因子的量化处理。如果直接用与待预测日的时间距离来量化时间因子,会导致时间因子与顶层油温的相关性较小,不符合实际情况,故本文提出了一种基于顶层油温大小模糊排序的时间因子量化处理方法,具体步骤如下。
(1)对E个历史样本中时刻j的特高压主体变压器顶层油温按高低进行排序,当顶层油温取得最大值时,时间因子中间变量Hij赋值为E,当顶层油温取得第二大值时,Hij赋值为E-1,依此类推,当顶层油温取得最小值时,Hij赋值为1。
(2)计算E个历史样本中时刻j的特高压主体变压器顶层油温在全天24个时刻的占比Zj。

式中:C0为常数;uij为影响因素,u=W,S,J,G,F,Q,T,P。
3)计算8 种影响因素的简单相关系数。将E个历史样本中环境温度、空气湿度、降雨情况、光照强度、风速等级、环境气压、时间因子和负荷因子这8种影响因素的日平均值作为自变量,将E个历史样本中特高压主体变压器顶层油温的日平均值作为因变量,然后由1.1节即可得到各因素的简单相关系数。
1.3 主要影响因素分析
本文以华东地区某特高压变压器6—8 月主体变压器顶层油温数据作为历史样本,该特高压变压器为西安西电公司生产,型号为ODFPS-1000000/1000,负荷率平均值为18.04%。为分析顶层油温的主要影响因素,利用通径分析方法计算了8 种影响因素的简单相关系数,结果如表1所示。
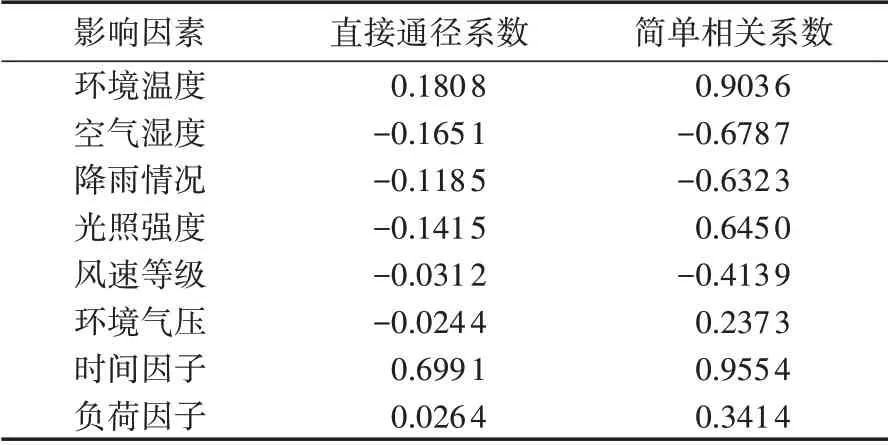
表1 通径分析方法的计算结果Table 1 Calculation results of path analysis method
分析表1 中的简单相关系数可知,特高压主体变压器顶层油温与环境温度、光照强度、环境气压、时间因子和负荷因子5 种影响因素呈正相关关系,与空气湿度、降雨情况和风速等级这3 种影响因素呈负相关关系。同时根据简单相关系数定义[25-26]可知,当简单相关系数的绝对值小于0.3 时,表示弱相关或无相关;当简单相关系数的绝对值大于等于0.3时,表示中等相关或强相关,因此本文选择简单相关系数绝对值大于等于0.3 的7 种影响因素,即环境温度、空气湿度、降雨情况、光照强度、风速等级、时间因子和负荷因子作为特高压主体变压器顶层油温的主要影响因素。
2 基于简单相关系数的综合因素相关度计算
相似日法是选择与待预测日相似度较高的历史样本日作为研究对象,本文借鉴该思路,进一步细化到时刻,提出相似时刻法,即选择与待预测时刻相似度较高的历史样本时刻作为研究对象来进行预测。根据简单相关系数的分析结果可知,本文将主要研究待预测时刻与历史样本时刻在7 种主要影响因素下的综合相关度。由于7 种主要影响因素可分为气象因素、时间因子和负荷因子3 类,因此本文将从气象因素、时间因子和负荷因子3 个方面来计算综合因素相关度。
2.1 气象因素相关度
根据前文分析可知,气象因素主要包括环境温度、空气湿度、降雨情况、光照强度和风速等级。本文借鉴TOPSIS 法的思路,利用各时刻气象因素与最优气象因素的距离来衡量气象相关度。根据特高压主体变压器顶层油温与环境温度、空气湿度、降雨情况、光照强度和风速等级的相关性,定义最优气象因素MY和最差气象因素MC如式(8)所示。

式中:MY1—MY5和MC1—MC5分别为特高压主体变压器顶层油温与环境温度、空气湿度、降雨情况、光照强度、风速等级的最优距离和最差距离。
考虑到5 种气象因素的简单相关系数不同,故各因素在与最优气象因素距离中的占比不同,因此本文提出基于简单相关系数优化的TOPSIS法。
根据TOPSIS 法的原理可得正向距离TZij如式(9)所示。

2.2 时间因子相关度
根据时间“距离远则相关性小,距离近则相关性大”的原则,利用与待预测日的距离衡量待预测时刻与历史样本时刻的时间因子相关度Bi。本文假设时间因子相关度Bi随着时间距离的增加线性递减,待预测日前第1天相关度取得最大值(1+C0)/(1+2C0),待预测日前第E天相关度取得最小值C0/(1+2C0),则待预测日前第i天的时间因子相关度Bi可以表示为:
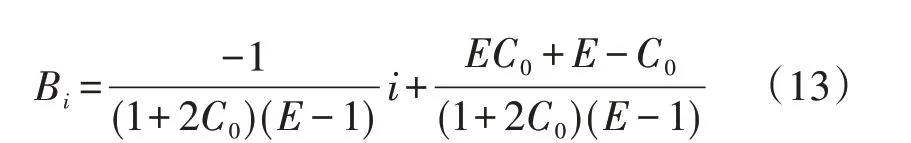
2.3 负荷因子相关度
显然2 个时刻的负荷值相差越小(越大),负荷因子相关度越大(越小),则待预测日前第i天时刻j与待预测日时刻j的负荷因子相关度Cij可以表示为:
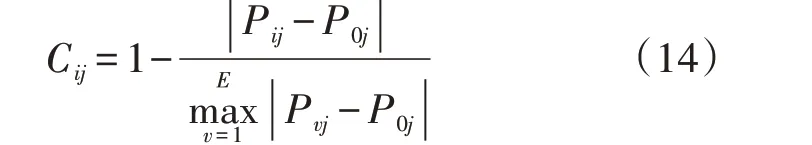
2.4 综合因素相关度
根据气象因素、时间因子和负荷因子相关度,本文采用基于简单相关系数加权得到综合因素相关度Dij为:
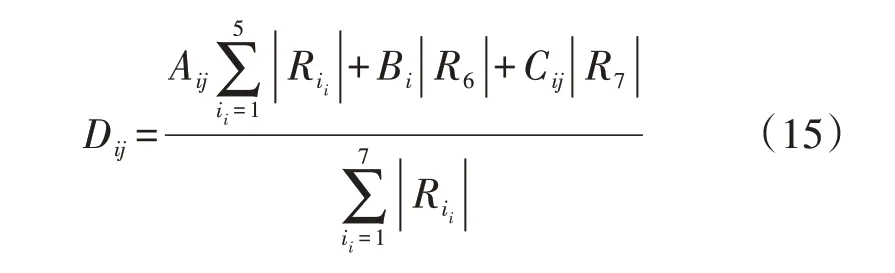
式中:R6、R7分别为时间因子、负荷因子的简单相关系数。
将上述综合因素相关度计算过程中的简单相关系数替换为直接通径系数,即可得到基于直接通径系数的综合因素相关度,本文不再赘述,下文将基于直接通径系数和基于简单相关系数2 种情况进行分析。
3 特高压变压器顶层油温预测
基于通径分析和相似时刻的特高压变压器顶层油温预测流程图如附录A 图A1 所示,具体步骤如下。
1)利用待预测日前40 组顶层油温数据作为参数计算样本,其中前10 组顶层油温数据作为参数计算的待预测样本,剩余30 组顶层油温数据作为参数计算的历史样本。
2)初始化设置综合因素相关度极限值CM和相似时刻最小数量NM。
3)计算待预测样本中各时刻与历史样本中各时刻的综合因素相关度Dij。
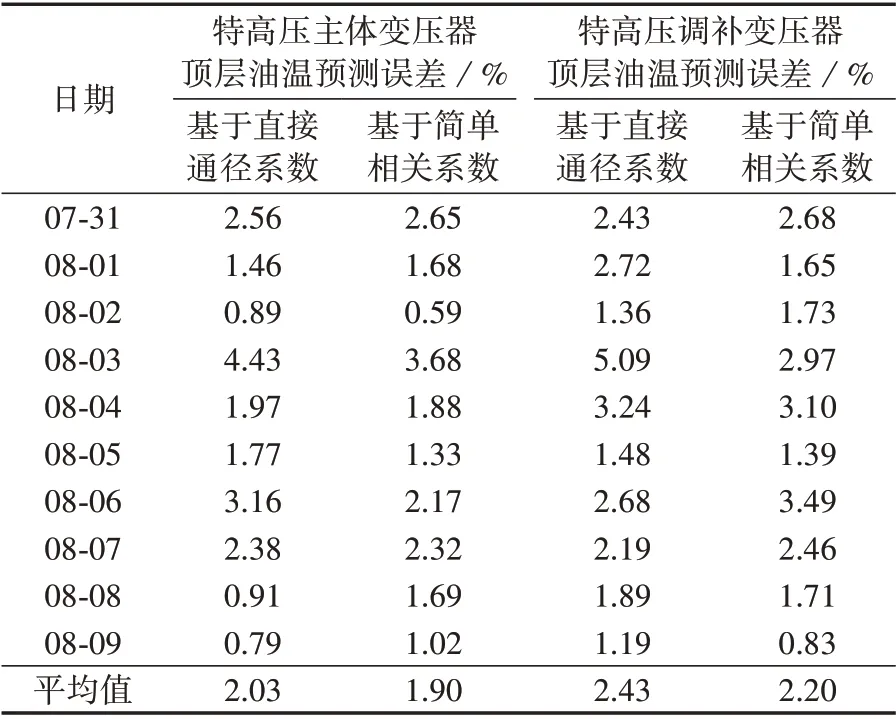
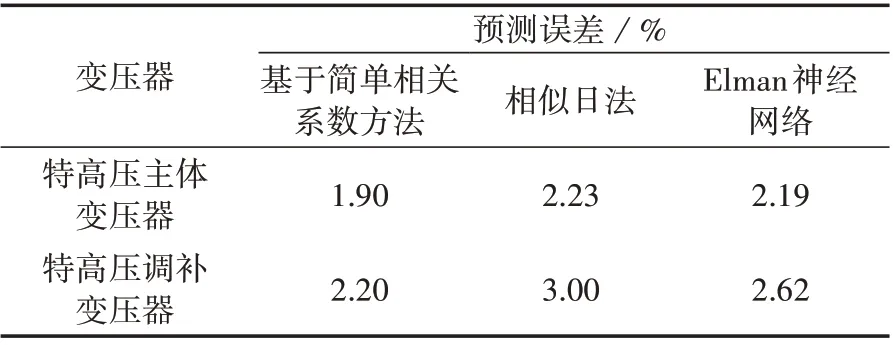
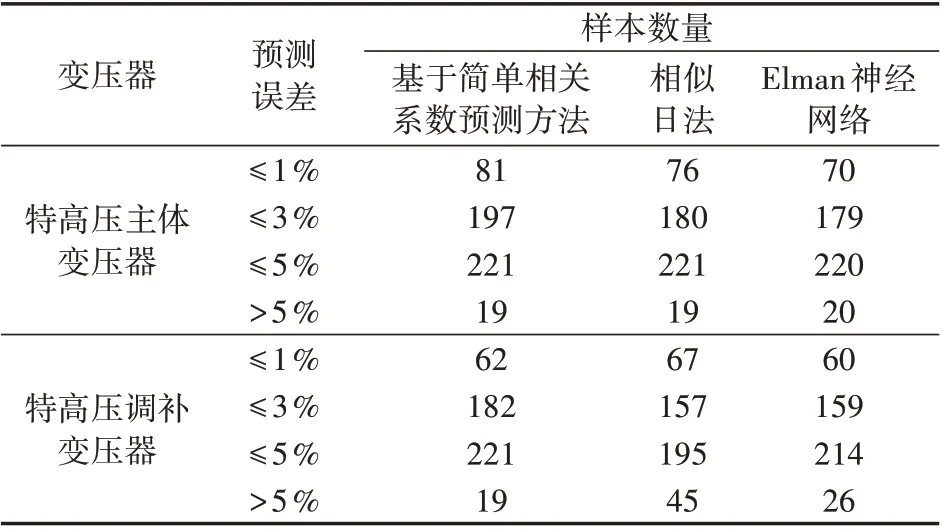
4)计算待预测样本在时刻j满足Dij≥CM的时刻数量NC,当NC≥NM时,认为NC个时刻都为相似时刻;当NC 5)选择相似时刻后,采用基于综合因素相关度加权和外推法的平均值作为预测值,具体的计算过程如下。 (1)根据式(16)计算基于综合因素相关度加权法预测的时刻j的顶层油温值MC1j。 式中:NT为相似时刻数量中间变量;Ij(i0)为待预测日时刻j的第i0个相似时刻对应的历史样本;DIj(i0)j为待预测日前第Ij(i0)天时刻j与待预测日时刻j的综合相关度;MTIj(i0)(j)为待预测日前第Ij(i0)天时刻j的顶层油温。 (2)根据式(17)计算基于外推法预测的时刻j的顶层油温值MC2j。 6)根据式(19)计算待预测样本所有时刻的预测值与实际值的相对误差平方和ER(CM,NM)。 式中:MT0(j)为待预测日时刻j的实际顶层油温。 7)判断ER(CM,NM)是否取得最小值。若ER(CM,NM)取得最小值,则对应的CM和NM即为模型最优参数,转至步骤8);若ER(CM,NM)未取得最小值,则回到步骤4)并改变CM和NM值后重新计算。 8)利用待预测日前30 组油温数据作为算法验证的历史样本。 9)将步骤7)计算得到的最优参数代入式(18),即可实现顶层油温预测。 需要特别说明的是,本文方法主要适用于预测特高压变压器未来1 天或几天的短期顶层油温,当预测未来1 个月或几个月的中长期顶层油温时,无法保证预测精度。实际上,预测顶层油温的目的是实时评估特高压变压器的热状态,即应重点关注的是特高压变压器短期顶层油温,而研究中长期顶层油温的意义较小。因此,本文方法对实时评估特高压变压器热状态、保证安全运行具有重要意义。 以华东地区某特高压变压器2018 年6 月21 日至2018年8月9日的50组顶层油温数据作为算例来验证所提预测方法的有效性。 将华东地区某特高压变压器2018 年6 月21 日至2018 年7 月30 日的40 组顶层油温数据作为参数计算样本,训练结束后,可得本文方法的最优参数如表2所示。 表2 最优参数Table 2 Optimal parameters 分析表2 可知,基于直接通径系数选择相似时刻时,相似时刻数量在3~30 范围内变化,而基于简单相关系数选择相似时刻时,相似时刻数量在5~30范围内变化,从而实现相似时刻的动态优化。 得到最优参数后,即可实现相似时刻的选择。下面以算法验证样本中2018 年7 月31 日的样本为例,分析该日所有时刻的相似时刻选择结果。为简化分析,针对基于直接通径系数选择相似时刻只给出综合因素相关度最大的3 个相似时刻,针对基于简单相关系数选择相似时刻只给出综合因素相关度最大的5个相似时刻,具体结果分别如附录B 表B1、B2 所示。由表B1 可知,采用基于直接通径系数选择相似时刻时,相似时刻对应的日期基本都在待预测日前3 天,表明该方法在选择相似时刻时,时间因子占据较大比重,而表1 中时间因子的直接通径系数为0.6991,远大于其他因素,算例分析结果符合表1 的计算结果。同理分析表B2 可知,采用基于简单相关系数选择相似时刻时,相似时刻对应的日期不限于待预测日前5 天,表明该方法在选择相似时刻时,除时间因子外,还有其他影响因素占据较大比重,而表1 中环境温度的简单相关系数为0.903 6,时间因子的简单相关系数为0.955 4,都占据较大的影响比重,因此算例分析结果符合表1的计算结果。 为进一步分析,绘制基于直接通径系数和简单相关系数的相似时刻顶层油温示意图分别如图1(a)、(b)所示。结合图1,基于直接通径系数和简单相关系数选择的相似时刻的顶层油温均在待预测时刻顶层油温附近变化且波动幅度较小,从而验证了相似时刻选择结果的有效性。 图1 相似时刻顶层油温Fig.1 Top oil temperature of similar time 利用本文提出的预测方法对算法验证样本中2018 年7 月31 日 至2018 年8 月9 日 的10 组 顶 层 油温进行预测,结果如图2 所示。由图可见,基于直接通径系数和简单相关系数预测的顶层油温曲线与实际顶层油温曲线的变化趋势均基本一致,且部分时刻基本重合。 图2 顶层油温预测结果Fig.2 Forecasting results of top oil temperature 为进一步分析,绘制顶层油温预测误差(即相对实际油温的误差)如图3 所示,显然2 种预测方法对特高压主体变压器和特高压调补变压器的顶层油温预测误差基本都小于5%,具有较高的预测精度。 图3 顶层油温预测误差Fig.3 Forecasting error of top oil temperature 2 种方法的预测误差对比如表3 和附录B 表B3所示。由特高压主体变压器顶层油温的预测结果可见,基于简单相关系数、直接通径系数方法的平均预测误差分别为1.90%、2.03%,平均标准差分别为0.013 3、0.014 6,最大相对误差分别为8.51%、9.12%,显然基于简单相关系数方法的预测精度更高,误差波动更小,预测效果要好于基于直接通径系数的方法。从特高压调补变压器顶层油温的预测结果可以得到相同的结论,从而验证了基于简单相关系数方法的有效性。 表3 2种方法的预测误差Table 3 Forecasting errors of two methods 为验证基于简单相关系数预测方法的有效性,本文采用相似日法和Elman 神经网络对该特高压主体变压器和调补变压器顶层油温进行了预测,结果分别如图4(a)、(b)所示。由图可见,无论是特高压主体变压器还是预测特高压调补变压器,采用基于简单相关系数方法的顶层油温预测值更加接近实际值,效果更好。 图4 不同方法的顶层油温预测结果Fig.4 Forecasting results of top oil temperature by different methods 为定量分析比较3种方法的预测精度,统计了3种方法的预测误差及对应的样本数量分别如表4 和表5所示。 表4 不同方法的预测误差Table 4 Forecasting errors of different methods 表5 不同方法的预测误差样本数量Table 5 Sample numbers of forecasting errors of different methods 由表4 可见,基于简单相关系数方法的预测精度最高,Elman 神经网络次之,相似日法预测精度相对较低。由表5 中特高压主体变压器的统计结果可见,基于简单相关系数方法、相似日法、Elman 神经网络法的预测误差小于等于1%的样本数量分别为81、76、70,预测误差小于等于3%的样本数量分别为197、180、179,基于简单相关系数方法的预测效果显然优于其他2 种方法;从特高压调补变压器的统计结果可以得到同样的结论,从而验证了本文所提出的基于简单相关系数方法的有效性。 1)利用通径分析方法,计算了各影响因素的简单相关系数,分析了各影响因素与特高压变压器顶层油温的相关性,并选择环境温度、空气湿度、降雨情况、光照强度、风速等级、时间因子和负荷因子作为特高压变压器顶层油温的主要影响因素; 2)利用基于简单相关系数优化的TOPSIS 法分析了气象因素相关度,并基于时间“距离远相关性小,距离近相关性大”的原则分析了时间因子相关度,最后基于简单相关系数加权得到综合因素相关度; 3)通过华东地区某特高压变压器顶层油温数据对本文方法进行了验证,结果表明本文方法通过动态优化相似时刻数量,有效提高了预测精度,且基于简单相关系数方法的预测效果要优于基于直接通径系数方法。 附录见本刊网络版(http://www.epae.cn)。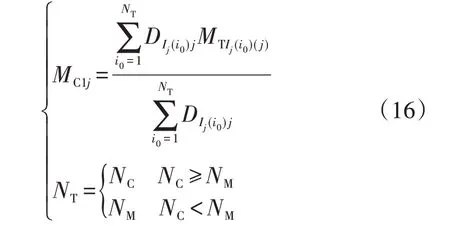

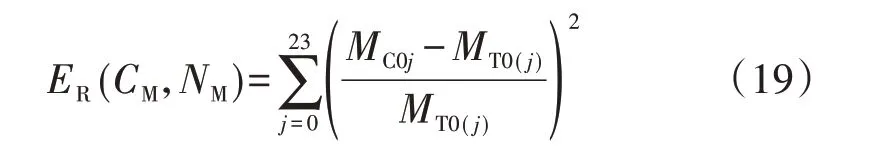
4 算例分析
4.1 相似时刻选择分析


4.2 特高压变压器顶层油温预测分析



5 结论
