基于模型预测控制的含岸电混合能源系统优化运行
2021-11-20张晓晴李泽宁王业庭王世丹
王 玮,张晓晴,苏 粟,李泽宁,王业庭,夏 冬,王世丹
(1. 北京交通大学 国家能源主动配电网技术研发中心,北京 100044;2. 国网新源控股有限公司,北京 100761;3. 国网天津市电力公司经济技术研究院,天津 276000;4. 国网北京市电力公司海淀供电公司,北京 100000)
0 引言
港口在国际贸易中发挥着关键作用,推动了世界经济的发展,然而港口也是大气污染的来源地。为减少污染物的排放[1],从电能产生的角度出发,港口利用可再生能源发电减少环境的污染,海上风能作为港口最丰富的可再生能源之一,结合海上风机可以为港口带来显著的环境效益[2]。从电能消耗的角度出发,港口鼓励船舶靠港期间使用岸电,岸电技术作为节能减排的新技术之一,虽然在某些地区仍然存在成本昂贵、技术标准不完善、政策不统一等问题[3],但是已经在中国、美国、加拿大、德国、瑞典、芬兰、挪威、荷兰和比利时等国家的某些港口实施[4],并且岸电技术的应用也显著减少了大气污染物的排放[1],风能与岸电加入港口形成由海上风机、岸电与储能等组成的混合能源系统[5]。
不包含岸电的混合能源系统与微电网具有一致性,目前国内外关于微电网优化运行的研究较为成熟,文献[6-7]考虑了风光出力与负荷需求的不确定性,但是缺少实时动态更新,未能不断地利用更新的预测信息进行优化。文献[8-9]均采用模型预测控制(MPC)方法进行微电网的动态滚动优化,MPC 方法使得决策根据实际情况不断做出优化调整,但是文献[8]未考虑MPC 参数设定对优化结果的影响,文献[9]针对突发的扰动在优化中对MPC 参数进行自适应调整,但是并未将其作为优化的决策变量。考虑混合能源系统内港口负荷中常含有高频功率波动的特殊性,其预测误差较大,并且海上风机属于不可控的发电设备,同样具有功率的波动性,预测误差较大,因此本文采用MPC 方法根据系统不断更新的信息进行滚动优化,并将MPC 参数作为优化变量求解出不受参数设定值影响的最优结果。
含岸电的混合能源系统与微电网具有差异性,目前国内外关于包含岸电与海上风机的混合能源系统的优化运行研究较少,文献[10-12]从靠港船舶电力用户的角度出发,以降低船舶用电成本为目标,提出了海上光伏/电池/柴油/岸电混合能源系统的优化运行方法,其中文献[10]对比了3 种岸电电价机制下4 种不同优化方法的优化结果,并得出采用分时电价机制会使船舶用电成本最小的结论。文献[13-14]从港区电网角度出发,以港口运营成本最小为目标,提出一种新的大型港口多目标作业调度方法,其可以降低作业成本,限制港口排放,支持港区电网。文献[5]和文献[15]从由风力/蓄能/岸电组成的可再生能源混合系统角度出发,为风机的装机容量和运行优化策略提供了一种方法,分析了风机制造商、风速条件、储能装机量与电网电价对风机安装容量的影响,但文献[5]和文献[15]较侧重于风机安装容量优化配置研究,优化策略研究相对较少。
本文以海上风机、岸电与储能组成的混合能源系统的运行成本最小为目标,采用MPC 方法进行系统的优化运行。首先,分别建立系统各部分的模型,其中岸电模型中的岸电价格考虑了岸电服务费的收取;然后,根据已建立的模型采用MPC 方法进行优化调度,建立以混合能源系统运行成本最小为目标的优化模型,采用CPLEX+YALMIP 求解混合整数非线性规划问题;最后,以某集装箱港口混合能源系统为例进行仿真分析,验证了优化方法的有效性。
1 含岸电的混合能源系统模型
港口岸电简言之,就是指停靠在码头的船舶可利用清洁、环保的“岸电”替代船舶辅机燃油供电,保证船舶各支撑设备系统的正常运作[16]。当船舶停靠在码头时,由岸电替代船舶辅机进行供电。本文的混合能源系统包括风力发电机、储能与岸电系统,如附录A 图A1 所示。风力发电机作为可再生能源起到了减排的作用,储能作为能量回收装置起到了节能的作用,岸电替代船舶辅机实现了节能减排。
集装箱码头中的电力负荷通常包括:作为装卸设备的电动起重机与靠港船舶的电力供应[15]。混合能源系统与电力负荷之间的功率流动关系如图1 所示。在船舶靠港进行装卸货期间,靠港船舶与电动起重机的电力供应由风力发电机、储能与岸电组成的混合能源系统提供,系统的运行策略如下:当风力发电机输出功率P1无法满足电力负荷需求时,增大配电网输出功率P2与储能放电功率P3;当风力发电机输出功率P1大于电力负荷需求时,增大储能充电功率P4以满足能量守恒。
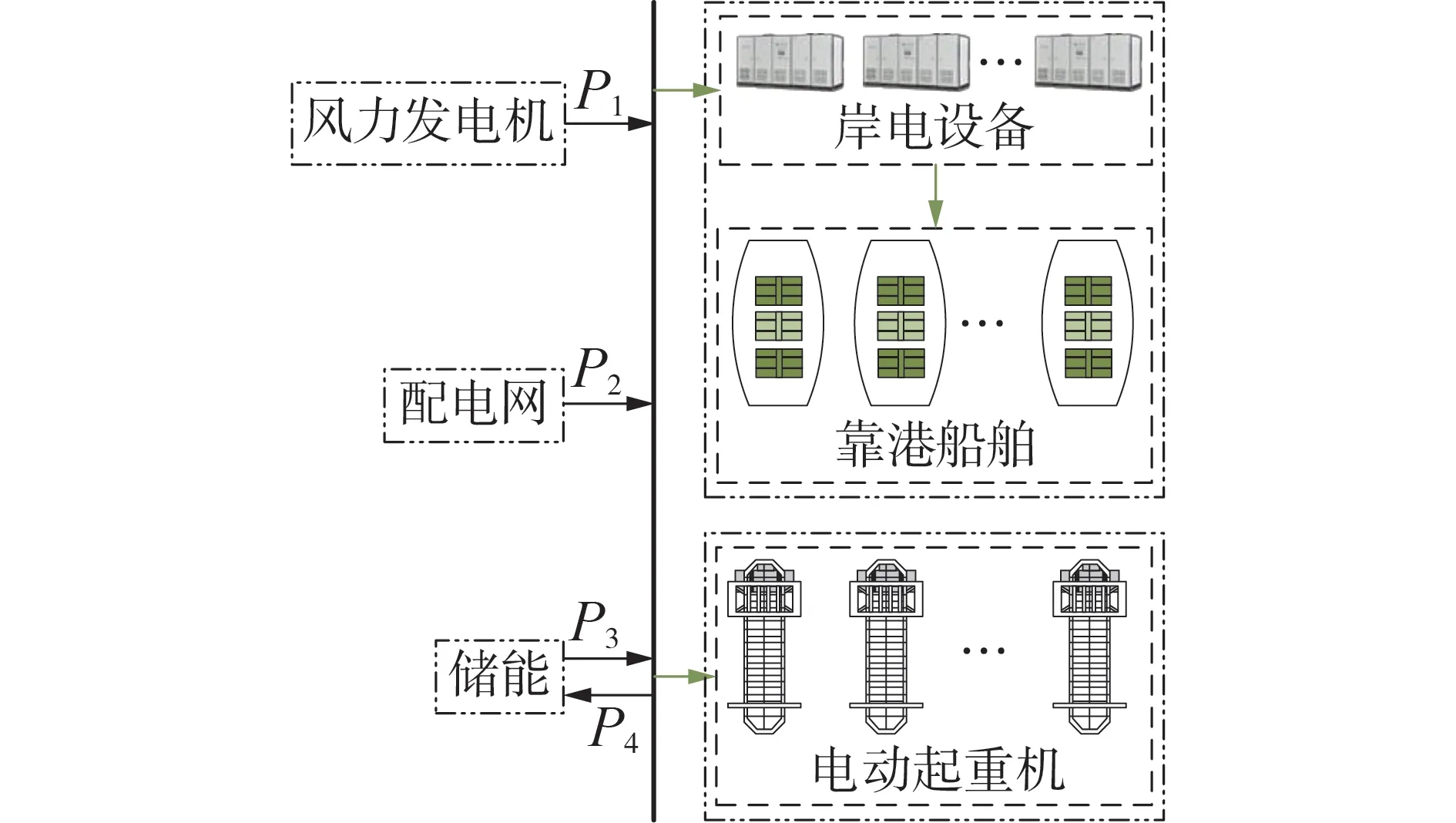
图1 混合能源系统功率流动示意图Fig.1 Schematic diagram of power flow for hybrid energy system
1.1 岸电模型
岸电技术是指陆上电力经过变频变压处理,接入船舶岸电装置为船舶的其他关键设备进行供电的技术。港口岸电技术的引入可以减少船舶靠港期间因船舶发电机燃料燃烧造成的大气污染物的排放,但会带来一系列的问题[16],其中与混合能源系统优化运行相关的主要是岸电的供售电机制不完善问题和接入岸电的靠港船舶负荷的不确定性问题,本文针对上述问题进行了动态电价模型与负荷预测模型的建立。
1.1.1 动态电价模型
我国提出新建码头应当规划、设计和建设岸基供电设施,已建成的码头应当逐步实施岸电设施改造,船舶靠港后应当优先使用岸电等鼓励岸电发展政策,但关于岸电的价格机制尚未确立统一的标准,根据文献[17]可知我国岸电价格由实际电价与岸电服务费组成,其模型如下:

式中:p(t)为t时刻岸电价格;ρ(t)为t时刻实际电价;c(t)为t时刻岸电服务费;θ为岸电服务费选择参数,可取为0 或1,取1 时表示该港口企业收取岸电服务费,取0时表示该港口企业不收取岸电服务费。
岸电作为港口提供给船舶的商业产品,港口可以通过调整岸电服务费吸引船舶使用岸电,以此获得更大利润,加快港口回收岸电综合投资成本。
根据靠港船舶岸电用电量的大小,建立线性阶梯服务费模型,计算公式如下:

当靠港船舶使用电力来自电网时,部分港口企业执行平均电价收费,部分港口企业执行分段高峰低谷收费[17]。执行平均电价收费的港口实际电价始终保持不变,执行分段高峰低谷收费的港口实际电价服从分时电价制度,该制度将一天分为3 个时间段,每个时间段的电价不同,分别称为峰时电价、谷时电价和平时电价[17]。上述电价模型均为固定电价,不具备负荷的追踪作用,动态电价模型根据负荷的变化调整电价,具体公式如下:
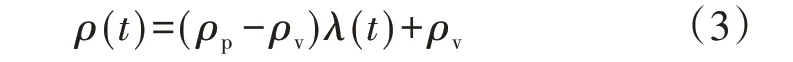
式中:ρp为峰时电价,本文取为1.35元/(kW·h)[17];ρv为谷时电价,本文取为0.47 元/(kW·h)[17];λ(t)为t时刻电价调整系数,当负荷功率较大或负荷用电量持续较大时设定电价调整系数为0,则电价为谷时电价;当负荷功率较小或负荷用电量持续较小时设定电价调整系数为1,则电价为峰时电价。
1.1.2 负荷预测模型
在确定岸电电力系统负荷时,由于船舶靠港时间、船舶离港时间、船舶靠港后需要运行的设备功率、启动次数和持续工作时间一般带有随机性质,而且不同类型船舶靠港后用电负荷也千差万别,所以对其进行精确计算是比较困难的[18],但是负荷数据不仅具有随机性,而且具有趋势性、相似性与周期性,在相同日类型下负荷变化趋势相同,可用短期预测模型对其进行估算,预测模型的建立步骤包括负荷预测影响因素的确定、负荷预测数据分析、负荷预测数据处理,具体如下。
1)负荷预测影响因素的确定。
靠港船舶负荷预测主要影响因素为船舶停靠行为,其中包括船舶类型、船舶到港时间与船舶离港时间等,具有时间分布随机性。与船舶停靠行为精确的机理建模相比,基于统计数据进行船舶停靠行为模拟的蒙特卡洛方法具有计算简单的优点,蒙特卡洛模拟法主要包括概率统计数据输入、随机抽样与蒙特卡洛模拟等步骤,根据船舶历史行为数据模拟得出船舶停靠行为如图2 所示。图中,σ为船舶“充电”行为模拟数据,其数值越大表示该时刻停靠船舶数量越多、停靠船舶吨位等级越大。
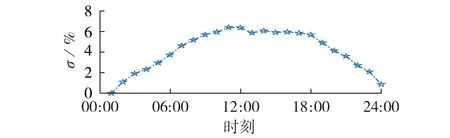
图2 船舶停靠行为模拟图Fig.2 Simulation diagram of ship docking behavior
2)负荷预测数据分析。
船舶靠港后由于间歇工作设备的存在产生了非平稳突变信号,增大了负荷数据的分散性,而采用人工智能方法进行负荷预测时,历史负荷数据的分散性直接影响负荷预测结果的精确度和收敛性。小波包分解(WPT)在处理非平稳突变信号时具有良好的局部化和多分辨率特性[19],适用于历史负荷数据波动分析。设定WPT 层数b=3,小波基函数为db6,重构第b层频段的负荷分量,得到2b个频段分量,以历史负荷数据为例仿真得到各频段能量分布如图3 所示。低频段(频段1)信号能量占比大,变化平缓,分散性小,适用于精确度较高、收敛性较差的负荷预测方法,如深度置信网络(DBN)[20];中频段(频段2、3)与高频段(频段4—8)信号能量占比小,分散性大,适用于精确度较低、收敛性较好的负荷预测方法,如BP神经网络。

图3 各频段能量分布Fig.3 Energy distribution for each frequency band
3)负荷预测数据处理。

式中:psl/w为负荷或者风速数据归一化结果;Psl/w为负荷或者风速原始数据;P(sl/w)max为负荷或者风速数据的最大值;P(sl/w)min为负荷或者风速数据的最小值。
1.2 储能模型
由图1 可知,储能充电功率为P4,储能放电功率为P3,储能的荷电状态SOC(State Of Charge)随充放电功率动态变化,具体如式(6)所示。

1.3 风机模型
风力发电机输出功率与风速呈某种函数关系,如式(7)与附录A图A2所示[21]。
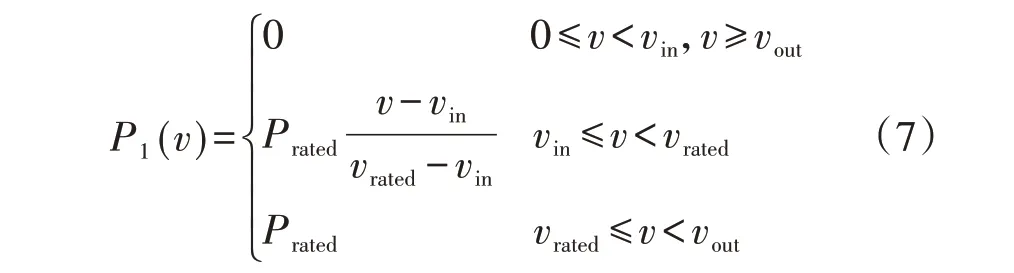
式中:Prated为风机的额定功率;vin为风机的切入风速;vout为风机的切出风速;vrated为风机的额定风速;P1为风机的输出功率。
当风速小于风机切入风速或者大于等于风机切出风速时,风机输出功率为0;当风速大于等于切入风速并且小于风机额定风速时,风机输出功率与风速成正比;当风速大于等于额定风速并且小于切出风速时,风机输出功率为额定功率。
本文采用的风速服从威布尔分布[22],年小时平均风速的概率密度分布如附录A图A3所示。
2 混合能源系统优化运行
本文采用MPC 方法进行优化的原理如图4 所示。图中,k为优化次数;ΔT等于控制时域NP,mΔT等于预测时域N。当k=1 时,利用负荷、风电在预测时域内预测的数据在控制时域NP内进行优化求解并得出调度计划,仅保留t0时刻到t0+1 时刻的调度计划并执行;当k=ΔT+1 时,预测时域、控制时域右移ΔT,同样进行控制时域内的优化求解并保留t0+ΔT时刻到t0+ΔT+1 时刻的调度计划,依此类推,重复滚动[23]。
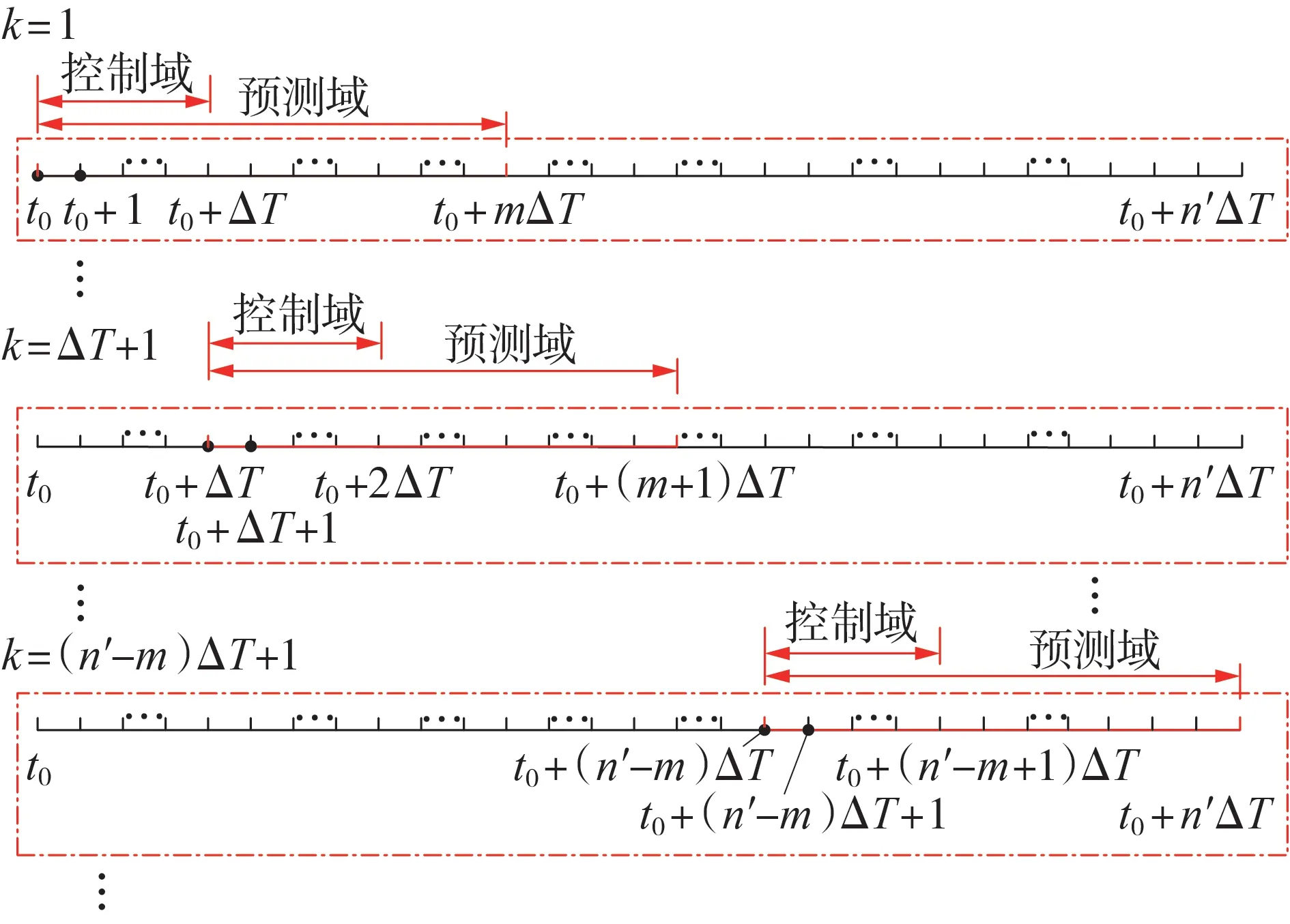
图4 MPC方法原理图Fig.4 Principle diagram of MPC method
本文中MPC 采用状态空间模型,如式(8)所示,模型中状态量为储能荷电状态SSOC,控制量为混合能源系统各功率。

2.1 滚动优化模型
2.1.1 目标函数
滚动优化模型以混合能源系统运行成本最小为目标函数,具体公式如下:

滚动优化模型不等式约束条件包括储能容量与功率最大值和最小值约束。
1)储能容量约束。
本文选用储能SSOC处于35%的条件下保存性能最佳,因此容量约束如下:

2.2 优化策略

遗传算法中采用了二进制编码,编码长度为NP的取值范围,即1~N*(N*为优化时间周期,且N*=N),取值约束条件为能被优化时间周期N*整除,具体处理形式如下:
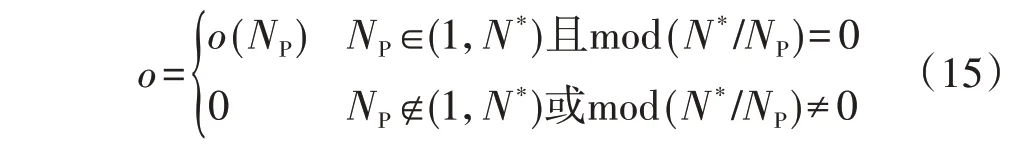
式中:o为目标函数取值;mod(N*/NP)为N*除以NP的余数。当N*=24 时,NP的取值范围为1~24,且NP应能被24 整除,即NP为2、3、4、6、8、12,相对应的二进制编码为0010、0011、0100、0110、1000、1100。
3 算例分析
本文研究选取某集装箱港口靠港船舶负荷历史数据,如附录A 图A5 所示,分别采用3 种预测方法进行仿真,得出如图5所示的预测结果。方法1利用WPT 将负荷信号分解为低、中、高3 个频段,针对低频段信号变化平稳、分散性小的特点,预测方法采用预测精确度较高的DBN;针对中、高频段信号分散性大的特点,预测方法采用收敛性较好的BP 神经网络。作为对比,方法2 仅采用BP 神经网络预测,方法3仅采用DBN模型预测。
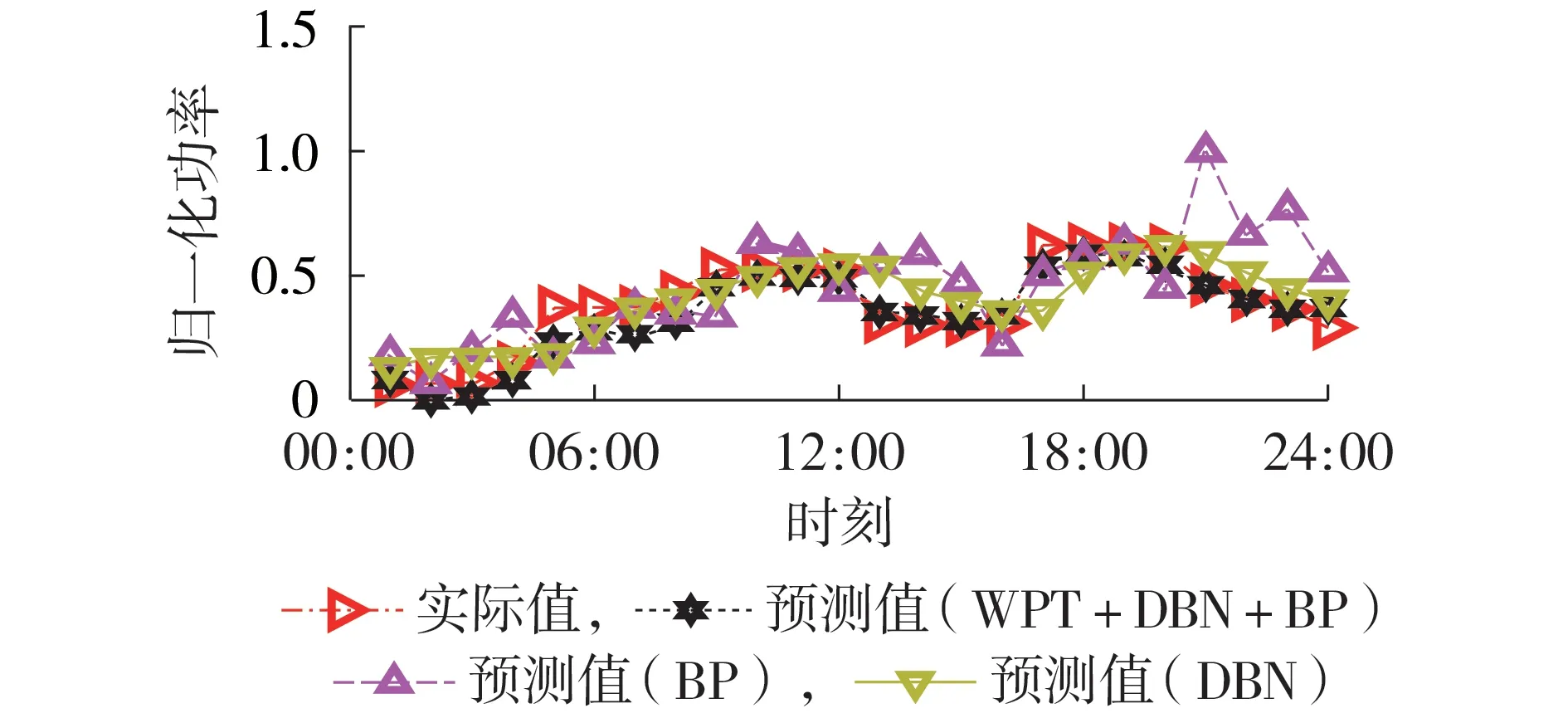
图5 负荷预测结果对比Fig.5 Comparison of load forecasting results
由图5 可知:相较于方法1、3 的预测结果,方法2的预测结果明显与实际值相差更大,在3种方法中BP神经网络预测误差最大;在不同时刻,方法3与方法1的预测值与实际值的差值不同,在[06:00,08:00]时段方法3的预测误差较小,其他时刻方法1的预测误差较小。为精确比较各种方法的预测结果的精确度,提出平均绝对百分比误差与准确率2 个指标,计算公式分别如式(16)与式(17)所示,经过计算得出3种方法的精确度评估参数如表1所示。可以看出,方法1 的平均绝对百分比误差小于0.1,明显低于方法2 与方法3,且方法1 的准确率大于0.9,明显高于方法2与方法3。
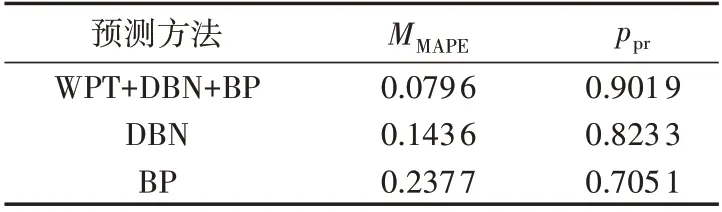
表1 不同预测方法的结果对比Table 1 Comparison of results among different forecasting methods
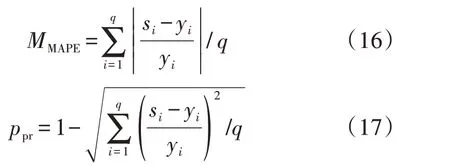
式中:si和yi分别为第i个数据的预测值和实际值;q为预测数据向量维数;MMAPE为平均绝对百分比误差;ppr为准确率。
从3 种方法的预测精确度评估指标值可以得出方法1 具有较高的准确度与较低的预测误差的优点,但是在采用方法1进行预测时,设定不同的WPT层数会得出不同的预测结果,如表2所示。由表1与表2 可以看出,负荷预测的准确率与WPT 层数呈非线性关系,在b取3时,负荷预测的准确率最高,当选定不合适的WPT层数时,方法1的准确率降低,低于方法2 预测准确率(如b取4、5、6),甚至低于方法3预测准确率(如b取5)。因此,需比较不同WPT层数下预测结果准确率,最终确定预测准确率最优的分解层数。
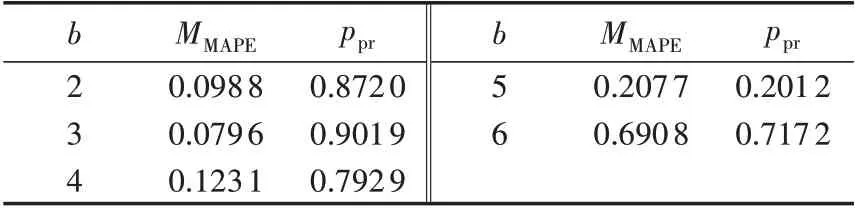
表2 不同WPT层数的结果对比Table 2 Comparison of results among different values of b
根据负荷预测结果与某集装箱港口起重机负荷数据,采用MPC 方法进行仿真优化,该集装箱港口设有5 个含岸电设施的泊位,仿真数据如附录A 图A6 所示,各个模型中的仿真参数及其取值如附录A表A1所示。
1)控制时域NP的选取对优化结果的影响。
采用MPC 方法时需确定控制时域与预测时域,预测时域根据系统需求确定,控制时域的选取范围在预测时域之内,且能整除预测时域。附录A 图A7描述了不同预测时域下,不同控制时域与优化目标和算法复杂度之间的关系。
图A7(a)中不同预测时域下,控制时域与序号的对应关系见附录A表A2。由图A7(a)所示的关系图可以得出:随着控制时域的增大,优化目标逐渐减小,即系统运行成本逐渐减少,在控制时域增大到某一定值后,优化目标基本不变,不再受控制时域的影响。由表A2 可以得出:序号与控制时域成正比,则序号越大代表控制时域越大,序号越小代表控制时域越小。
图A7(b)中不同预测时域下,控制时域与序号的对应关系见附录A表A3。由图A7(b)所示的关系图可以得出:随着控制时域的增大,优化算法的时间复杂度越大,即优化时间越长。由此可见,控制时域的确定不仅会影响算法的求解速度,也会在一定范围内对优化结果产生一定的影响,因此优化变量中应包含控制时域。由表A3可以得出:序号与控制时域成正比,则序号越大代表控制时域越大,序号越小代表控制时域越小。
2)滚动优化结果。
采用CPLEX+YALMIP 对混合整数变量进行优化求解,控制时域优化结果为NP=4,电价调整系数优化结果如附录A 表A4所示,电价调整系数与配电网输出功率归一化结果如图6所示。
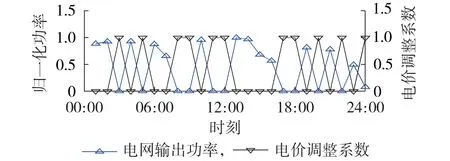
图6 电价调整系数与电网输出功率Fig.6 Price adjustment factor and output power of grid
由表A4 可以得出:当λ=1 时,电网电价为高电价;当λ=0时,电网电价为低电价。由图6所示的优化结果可得:当电价调整系数为1,即电价较高时,电网输出功率为0;当电价调整系数为0,即电价较低时,电网输出功率较大,实现了动态电价对电网负荷的跟随。除此之外,动态电价模型在混合能源系统优化运行中体现了不同于固定电价的优越性,具体如表3所示。
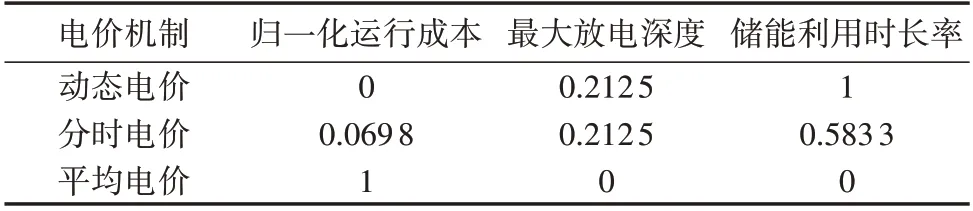
表3 不同电价模型的结果对比Table 3 Comparison of results among different electricity price models
由表3 可知,动态电价模型节省了电网交互成本,进而减小了系统运行成本。系统中储能的利用主要从储能的最大放电深度和储能利用时长率这2个方面体现。从最大放电深度而言,利用动态电价模型和分时电价模型时系统中储能均进入了浅层放电状态;从储能利用时长而言,利用动态电价模型时系统中储能的利用率最高,储能的利用起到了削峰填谷的作用,并且减少了运行成本,且储能利用得当,未进入深层放电状态,延长了储能的使用寿命。
实数变量的滚动优化求解结果如图7 所示。由图可得:由于在[08:00,09:00]、[11:00,12:00]时段实际电网电价为高电价,这2 个时段内配电网输出功率P2为0(如图7(a)所示),所以负荷功率主要由风机、储能补偿;储能在低电价时储存电能(如图7(b)中[13:00,16:00]时段所示),高电价时释放电能(如图7(b)中[08:00,09:00]、[11:00,12:00]时段所示),从而实现低储高发,减少系统运行成本。
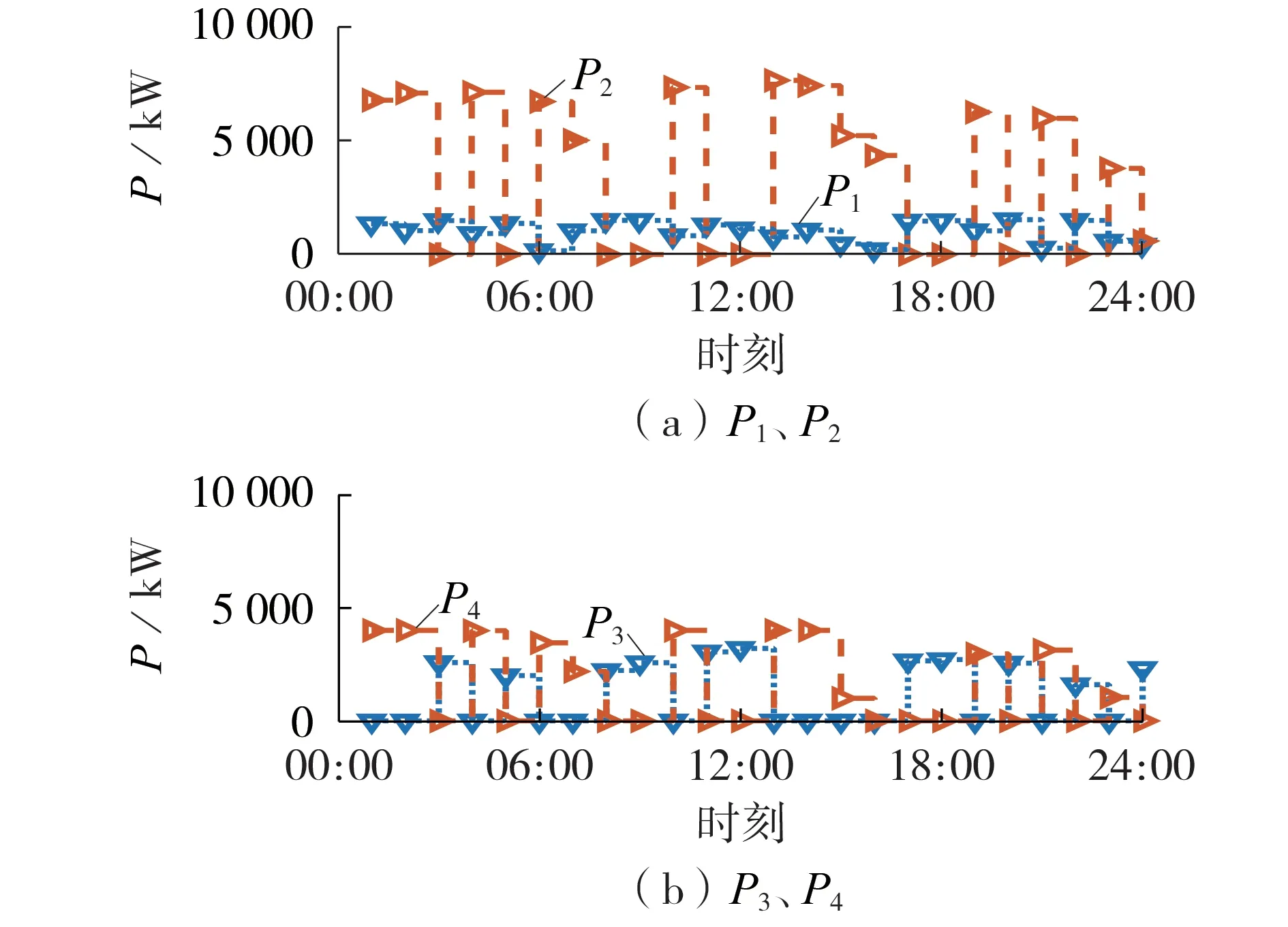
图7 滚动优化结果Fig.7 Results of rolling optimization
3)采用MPC方法的必要性。
本文研究采用MPC 优化方法改善开环优化方法在不确定性环境下误差较大的问题,为验证改善效果,采用指数平滑模型中的一次指数平滑预测作为扰动模型[26],一次指数平滑预测的数学模型如式(18)所示。

根据上述模型分别采用MPC 方法与传统优化方法进行优化求解,得出对比结果如图8 所示,图中变化率是指当前数据和下一个数据的差值与当前数据的比值。由图8 可以看出:随着不确定度的增大,传统优化直接进行开环优化求解的优化结果变化率逐渐增大,而采用MPC 方法求解的优化结果基本不变,验证了MPC 方法在不确定性环境下具有良好的适应性。
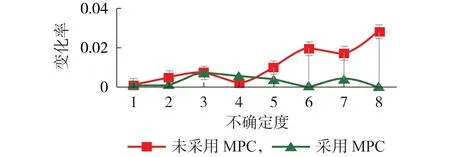
图8 MPC方法与传统优化方法的对比Fig.8 Comparison between MPC method and traditional optimization method
4 结论
本文提出一种针对港口中含岸电、海上风机、储能等混合能源系统的优化运行方法,采用MPC 进行滚动优化,利用CPLEX+YALMIP 进行求解,以某集装箱港口为例进行仿真分析,得到以下结论。
1)本文提出的分频段预测方法对波动性较大的负荷预测具有灵活性和良好的适应性,可根据不同的频段信号特点选择预测方法,在选定合适的WPT层数时,该方法相较于单一的负荷预测方法明显减小了预测误差。
2)本文提出的动态电价模型从2 个角度减小了系统的运行成本:从配电网角度而言,该模型减小了电网交互成本,进而减小了系统的运行成本;从储能角度而言,考虑储能的放电深度与充放电时长,该模型提高了储能的利用率,而储能利用率的提高减少了电网交互功率和系统运行成本。
3)MPC 方法是有反馈环节的闭环控制,采用一次指数平滑预测设定不同的不确定度的风机数据,对比开环控制与闭环控制在不确定度增加时的变化率,研究发现:MPC 闭环控制在不确定度增大时,相较于开环控制变化率基本保持不变。因此,MPC 方法在应对岸电的靠港船舶负荷与海上风机出力的不确定性时更具优势。
附录见本刊网络版(http://www.epae.cn)。
