CO2/CH4/N2 在MER 型沸石中扩散和分离的分子动力学模拟
2021-11-20石勤
石 勤
(兰州石化职业技术学院 应用化学工程学院,甘肃 兰州 730060)
CO2/CH4/N2混合气体的分离在天然气净化、煤层气开发及CO2捕获等工业方面具有重要的应用价值[1,2]。与传统的分离方法相比,吸附法和膜分离法因其设备简单、能耗低及腐蚀问题容易控制等优点而备受关注[3,4]。研发高效的吸附分离材料是吸附法和膜分离法工业化应用的关键技术,也是当前的研究热点之一。在已报道的MOF、炭材料、沸石及胺改性多孔固体等众多吸附分离材料中[5–7],MER 型沸石凭其特殊的三维八元环孔道结构以及良好的机械和物化性能,有望作为吸附剂或沸石膜在CO2/CH4/N2混合气体分离方面发挥重要作用。
近年来,人们对MER 型沸石分离混合气体开展了初步研究。Yeo 等[8]采用水热法制备了厚度~4.5 μm 的MER 型沸石膜,研究表明,沸石膜的渗透率为6.2 × 10−7mol/(s·m2·Pa),CO2/CH4的选择性高达77.5。Mirfenderesk[9]考察了MER 型沸石膜的制备条件对分离CO2/CH4的影响,研究指出,MER型沸石膜是一种性能优异的分离材料。Georgieva等[10]研究了不同阳离子交换的MER 型沸石对CO2/CH4的吸附性质,研究发现,K+交换的MER 型沸石(K-MER)对CO2具有较大的吸附能力(3.5 mmol/g,298 K,100 kPa 下)以及快速的吸附和脱附动力学性能。Choi 等[11]制备了不同Si/Al 和阳离子的MER型沸石,并将其用于CO2/CH4/N2混合气体的吸附分离,结果表明,MER 型沸石骨架Si/Al 和骨架外阳离子对CO2的高选择性吸附均具有很大影响。本课题组[12]采用蒙特卡洛模拟方法揭示了MER型沸石结构与气体吸附性能之间的构效关系,与其他沸石对比发现,MER 型沸石对CO2具有更大的吸附量,且具有超高的吸附选择性。上述研究均表明,K-MER 型沸石是一种极具应用潜力的吸附剂或沸石膜材料。但目前关于CO2/CH4/N2在MER型沸石中扩散和分离的动力学性质的研究报道极少,缺乏基础数据,仍需要进一步研究。从分子水平上深入认识气体分子在沸石限域空间中的扩散和分离机制,对高效沸石的设计制备及应用研究具有重要的理论指导意义。
本研究借助Material Studio 2017 模拟软件,以纯硅MER 型沸石(Si-MER)作为对照,在吸附性质研究的基础上,采用分子动力学(MD)模拟方法系统地探究CO2/CH4/N2在K-MER 型沸石中的扩散和分离性质,模拟获得三种气体分子在K-MER 型沸石中的自扩散系数、影响扩散行为的因素以及混合气体的分离选择性和渗透率。模拟结果为MER型沸石有效分离CO2/CH4/N2提供理论依据和实验指导。
1 计算模型和方法
1.1 计算模型
MER 型沸石是一种稀有的三维八元环微孔沸石,详细的结构介绍参考文献[12,13]。本文的沸石模型包括纯硅MER 和K-MER 型沸石。纯硅MER型沸石在实验中未见报道,模拟中用于和K-MER型沸石对比分析。沸石的骨架电荷由密度泛函理论(DFT) 计算获得[14],沸石骨架外的钾离子电荷为+1 价。为便于和实验(Si/Al = 3.8)[10,11]对比,模拟选取的K-MER 型沸石的骨架Si/Al = 3.57,沸石骨架Al 的取代位置由能量最小搜索法得到[14]。模拟过程中沸石骨架原子保持固定。模型构建中使用的力场均为COMPASS 力场[15]。
气体分子采用刚性模型,即气体分子的键长和键角在计算过程中均不发生变化。CO2中C−O键长为 0.118 nm,O−C−O 键角为180°,C 和O 的电荷分别为0.576 e 和−0.288 e;CH4和N2的原子电荷为0,CH4的C−H 键长为0.1092 nm,H−C−H 键角为109.47°,N2的N−N 键长为0.1109 nm[16]。
气体在MER 型沸石中的吸附模型和计算方法参考前期的研究[12]。气体在MER 型沸石中的扩散模型由4 × 4 × 4 的超晶胞组成。气体分子在沸石超晶胞中的吸附位置分布采用Sorption 模块中的 Locate 计算获得。
混合气体在K-MER 型沸石中的分离模型见图1 所示。模拟区域大小为2.85 nm × 2.98 nm ×14.26 nm。两个优化好的沸石膜和气体盒子通过建立层状结构晶体,并添加真空层,将模拟区域划分为三个部分。两个沸石膜中间的区域为气室,长度为5 nm;沸石膜两边的区域为真空层,称为侧室,长度均为2.5 nm。沸石膜的构建方法如下:采用1 × 2 × 2 的超晶胞作为沸石膜,首先沿着[1 0 0]方向对超晶胞进行表面切割,随后采用氢原子对切割表面的骨架氧原子进行饱和,最后采用DFT 对沸石膜优化并计算电荷。气体盒子的构建方法如下:采用Amorphous cell 模块,设置两种混合气体分子数分别300 个,通过调整混合气体密度的大小控制气体盒子的体积大小为2.85 nm ×2.98 nm × 5.00 nm,混合气体的初始分压相同,均为29.1 MPa(按理想气体计算)。最后对构建的气体盒子进行优化。

图1 混合气体分离模型Figure 1 Schematic diagram of mixed gas in separation model
1.2 计算方法
采用Forcite 模块进行MD 模拟。沸石中的原子和气体分子的力场参数均来自于COMPASS 力场,COMPASS(Condensed-phase Optimized Molecular Potentials for Atomistic Simulation Studies)力场是一个基于从头计算,已被证实能够准确预测孤立态和凝聚态分子的分子结构、振动、构象和热力学性质的分子力场,被广泛用于模拟多种分子在沸石中的吸附和扩散性质[17]。计算任务选择Dynamics,模拟系综选择NVT,控温方式为Andersen。在三维方向上运用周期性边界,静电作用采用Ewald方法,范德华作用采用 Atom based 方法。气体扩散模型中的模拟时间为1 ns,模拟步长为1 fs,每1 ps输出一帧。气体混合物分离模型中的模拟时间为5 ns,模拟步长为1 fs,每5 ps 输出一帧。
1.3 扩散模型中模拟时间的无关性验证
为了消除扩散模型中模拟时间对扩散模拟结果的影响,以N2在纯硅MER 型沸石中的扩散为例,在温度为298 K 下,考察了模拟时间分别为0.5、1 和2 ns 时N2的均方位移(MSD)与模拟时间的关系,见图2 所示。由图2 可知,在不同的模拟时间下,N2的MSD 与模拟时间均呈直线关系,且直线的斜率相差不大。所以扩散模型中模拟时间的大小对扩散模拟结果影响不大,可以忽略。由于扩散模型中的原子数达到2000 以上,延长模拟时间导致计算机CPU 运行时间大幅延长,对模拟造成困难。为此,本文扩散模型中的模拟时间选为1 ns。

图2 不同模拟时间下N2 在纯硅MER 型沸石中的MSD 与时间的关系Figure 2 MSD of N2 on silicon MER zeolite versus time at different simulated time at 298 K
2 结果与讨论
2.1 吸附性质
图3 和图4 所示为MER 型沸石在298 K 时的CO2、CH4和N2的吸附等温线和等量吸附热。由图3 可知,模拟得到的CO2、CH4和N2在K-MER型沸石中的吸附等温线与相同条件下的文献[10,11]实验值吻合,证明模型和力场是可靠的。

图3 CO2、CH4 和N2 在K-MER 与纯硅MER 型沸石中的吸附等温线Figure 3 Adsorption isotherms for CO2, CH4 and N2 on K-MER and silicon MER zeolites at 298 K

图4 CO2、CH4 和N2 在K-MER 与纯硅MER 型沸石中的等量吸附热Figure 4 Adsorption heat for CO2, CH4 and N2 on K-MER and silicon MER zeolites at 298 K
对比三种气体的吸附量和吸附热可知,CO2、CH4和N2在K-MER 和纯硅MER 型沸石中的吸附量和吸附热的大小顺序均为CO2> CH4> N2,三种气体在ZSM-5[18]与LTA[19]沸石中的吸附性质也表现出相同的规律。究其原因是,在三种气体中,CO2的极化率(29.1 × 10−25cm3)最高且具有最高的四偶极矩(4.3 × 10−26esu/cm2)以及最小的分子动力学直径(0.33 nm),故CO2与沸石之间作用力最强,较小的分子动力学直径对沸石的孔道利用率也最高,最终导致CO2的吸附量和吸附热最大。CH4的极化率(24.4 × 10−25cm3)次之,且无四偶极矩,分子动力学直径(0.38 nm)最大,所以CH4的吸附量和吸附热显著下降。N2的极化率(17.1 × 10−25cm3)最小,具有四偶极矩(1.5 × 10−26esu/cm2),分子动力学直径为0.364 nm,其吸附量和吸附热最小[18,19]。上述现象分析表明气体的分子的动力学直径、四偶极矩和极化率对气体的吸附均有较大贡献。
对比纯硅MER 和K-MER 型沸石可知,CO2、CH4和N2在纯硅MER 型沸石中的吸附量均大于其在K-MER 型沸石中的吸附量,根据前期研究[12],这是由于沸石骨架外阳离子的存在致使沸石的比表面积和空腔体积减小,故而吸附量减小。CO2在K-MER 型沸石中的吸附热显著大于纯硅MER型沸石,原因是沸石骨架外阳离子与CO2具有很强 作 用 力[20];CH4和N2在 纯 硅MER 和K-MER 型沸石中的吸附热大致相等,说明沸石骨架外阳离子对CH4和N2的吸附作用力影响不大。综合分析可知,沸石对吸附质的吸附量和吸附热的大小由沸石的结构、骨架外阳离子以及吸附质的性质等共同决定。
2.2 扩散性质
深入认识气体分子在沸石孔道中的扩散机制对理性设计制备高效分离材料及其工艺优化具有重要理论指导意义。扩散是一个宏观量,可以用扩散系数定量描述。自扩散系数描述的是粒子在没有浓度梯度的情况下,在孔道中的本征扩散,能够很好地反映分离材料的扩散性质[21]。本文通过模拟粒子运动轨迹获得均方位移(MSD) 与时间(t)的关系,并利用 Einstein 方程[22]计算粒子在沸石中的自扩散系数。
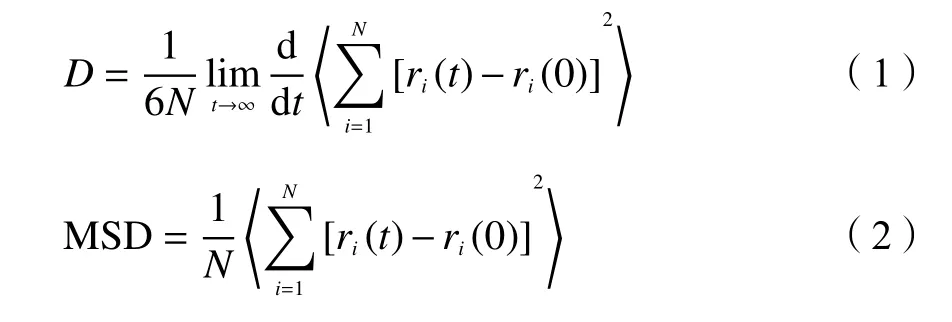
式中,D是自扩散系数,N是系统的粒子数,ri(t)是第i个粒子在t时刻的位置矢量。
在298 K,扩散模型中气体分子数均为80 时,CO2、CH4和N2在纯硅MER 和K-MER 型沸 石中的MSD 随时间的变化关系见图5 所示,相对应的自扩散系数见表1。从图5 中可以看到,CO2、CH4和N2在纯硅MER 和K-MER 型沸石中均存在亚扩散现象[23],即MSD 随模拟时间的延长先是快速增加,随后缓慢增加。原因在于MER 型沸石是八元环的笼状结构,在初始阶段气体分子在笼内扩散,不需要跨越能垒,扩散较快;随后是笼间扩散,需要跨越八元环窗口能垒,扩散变慢。
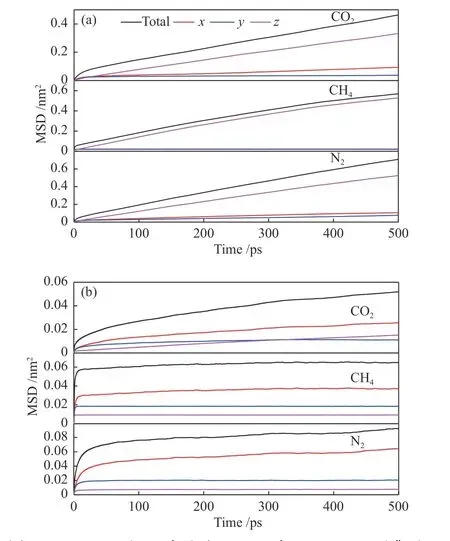
图5 CO2、CH4 和N2 在纯硅MER(a)与K-MER(b)型沸石中的均方位移与时间的关系Figure 5 MSD of CO2, CH4 and N2 on silicon MER (a)and K-MER (b) zeolites versus time at 298 K

表 1 CO2、CH4 和N2 在MER 型沸石中的自扩散系数Table 1 Self-diffusion coefficient of CO2, CH4 and N2 on MER zeolites at 298 K
从 表1 可 知,CO2、CH4和N2在 纯 硅MER 和K-MER 型沸石中的自扩散系数的数量级分别是10−10和10−12m2/s,所以它们的扩散方式均为构型扩散[24]。CO2、CH4和N2在纯硅MER 型中的自扩散系数远大于其在K-MER 型沸石中的自扩散系数,这说明沸石骨架外的阳离子阻碍了气体分子扩散,是影响气体分子在沸石中扩散能力的重要因素。
气体在纯硅MER 型沸石中的自扩散系数大小顺序是N2> CH4> CO2。为解释这一现象,分析了纯硅MER 型沸石的八元环窗口孔径(见图6)。由图6 可知,在x轴方向上连接pau 笼和ste 笼的八元环窗口孔径为0.5882 nm × 0.6582 nm,在y轴方向上连接pau 笼和ste 笼的八元环窗口孔径为0.5690 nm × 0.6396 nm,在z轴方向上连接pau 笼和d8R 笼及ste 笼和ste 笼的八元环窗口孔径分别为0.6761 nm × 0.7077 nm 及0.5896 nm × 0.7468 nm。纯硅MER 型沸石的三维八元环窗口孔径均大于CO2、CH4和N2的动力学直径,气体分子可自由穿过八元环,窗口孔径对气体扩散影响不大;影响气体分子在纯硅MER 型沸石中扩散能力的是气体与沸石之间的作用力,作用力越大(吸附热越大),扩散能力越小。

图6 纯硅MER 型沸石八元环窗口孔径Figure 6 Octet ring window aperture of silicon MER zeolite
CO2、CH4和N2在K-MER 型沸石中的自扩散系数大小顺序与纯硅MER 型沸石中的完全不同,这说明K-MER 型沸石中骨架外阳离子对气体扩散能力的影响大于气体与沸石之间作用力的影响。为了深入认识沸石骨架外阳离子对扩散的影响,结合沸石骨架原子和骨架外阳离子之间的径向分布函数(见图7)分析了其影响机制。径向分布函数指的是离给定粒子距离为r处,其他粒子出现的概率。因为MER 型沸石骨架外阳离子主要位于沸石的八元环窗口中[13],所以图7 所示的径向分布函数第一个峰的位置描述的是沸石八元环骨架原子和其环内钾离子之间的距离,即气体分子穿过八元环窗口的扩散直径。由图7 可知,沸石八元环骨架原子和其环内钾离子之间的距离在三维方向上各不相同。沸石骨架原子Al、Si 及O 与其环内K+之间的距离在x轴方向上分别是0.371、0.371 及0.289 nm;在y轴方向上分别是0.333、0.361及0.285 nm;在z轴方向上分别是0.345、0.355 及0.279 nm。沸石八元环骨架原子和其环内钾离子之间的距离介于CO2和CH4的动力学直径之间,导致CO2(动力学直径0.33 nm)容易穿过,N2(动力学直径0.364 nm)次之,CH4(动力学直径0.38 nm)最难通过。这很好地解释了为什么K-MER 型沸石中自扩散系数的大小顺序是CO2> N2> CH4,同时也为K-MER 型沸石高选择性分离CO2/CH4/N2提供了直接证据。
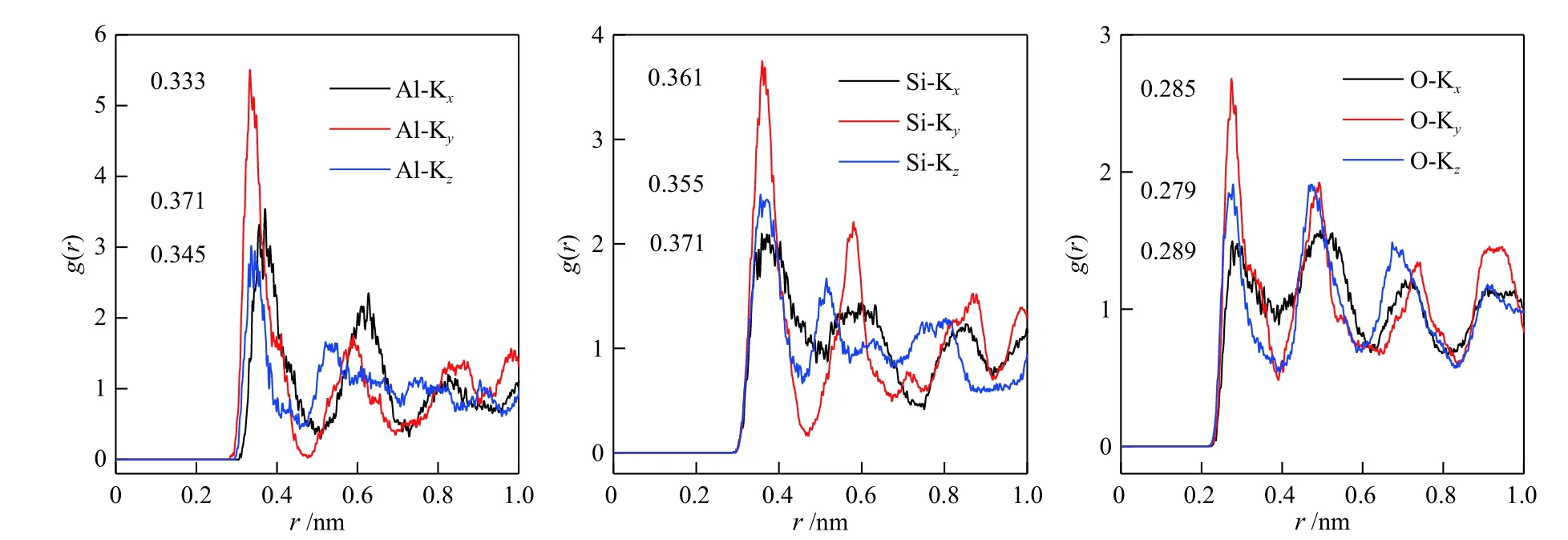
图7 K-MER 型沸石骨架原子与骨架外K+之间的径向分布函数Figure 7 Radial distribution function between the framework atoms and extra-framework K+ of K-MER zeolite
结合图5 和表1 还可以看出,CO2、CH4和N2在MER 型沸石三维通道中的扩散存在各向异性。在纯硅MER 型沸石中,气体分子优先选择在z轴方向扩散;在K-MER 型沸石中,气体分子优先扩散转变为x轴方向。这主要与气体分子在沸石中的扩散窗口孔径有关。在纯硅MER 型沸石中,z轴方向的扩散窗口孔径最大(见图6);而在K-MER型沸石中,由于K+的存在,改变了气体分子穿过八元环窗口的孔径,致使x轴方向的扩散窗口孔径最大(见图7)。这启示笔者在沸石膜的制备中,控制沸石膜沿着x轴定向生长,能够提高气体的扩散能力。
2.2.1 吸附质浓度的影响
在沸石孔道的限域空间中,吸附质的扩散速率与其浓度(压力)密切相关。根据三种气体各自的吸附量范围,温度为298 K 时,模拟得到了CO2、CH4和N2在K-MER 型沸石中的吸附浓度与自扩散系数的依赖关系见图8 所示。可以看出,CO2和N2的自扩散系数随吸附浓度的增加而减小。而CH4的自扩散系数随吸附浓度的增大出现先增加后减小的趋势,这与CH4在LTA、CHA 和ERI沸石中表现出的现象类似[25]。造成上述现象的原因是,气体的扩散性能与气体在沸石中的自由能有关,而气体在沸石孔道中的自由能分布随吸附浓度的变化而发生变化,自由能增加,扩散能力下降[25, 26]。
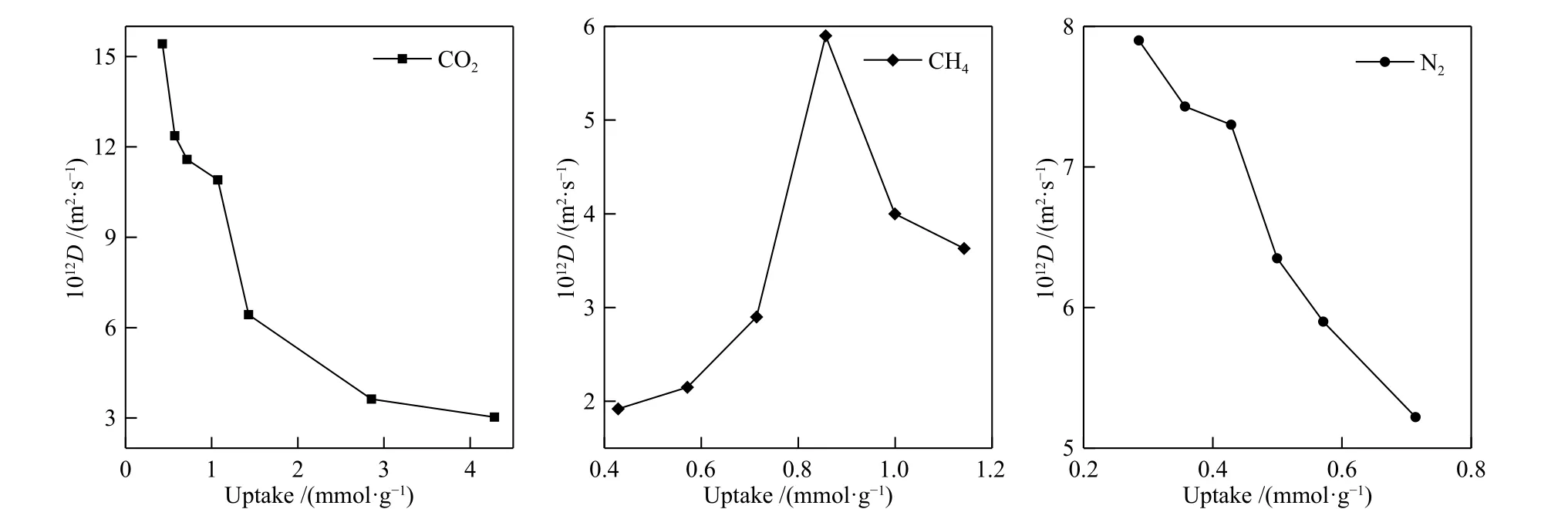
图8 CO2、CH4 和N2 在K-MER 型沸石中自扩散系数与浓度的关系Figure 8 Loading dependence of self-diffusion coefficients for CO2, CH4 and N2 on K-MER zeolites at 298 K
2.2.2 温度的影响
温度是影响扩散的另一个重要因素。气体分子在沸石限域空间中的自扩散系数(D)与温度(T)的依赖关系可以用Arrhenius 方程[27]描述:

式中,D0是扩散指前因子,Ea是扩散表观活化能,R是气体常数。
扩散模型中气体分子数为80,温度在278−368 K,CO2、CH4和N2在K-MER 型沸石中的自扩散系数与温度的拟合关系见图9 所示。随着温度的升高,CO2、CH4和N2的自扩散系数均增加。其中,N2的扩散活化能(Ea= 16.51 kJ/mol)最高,即随着温度的升高,其自扩散系数增加最快;其次是CH4,扩散活化能Ea= 8.39 kJ/mol;低温下CO2在KMER 型沸石中的扩散最快,但由于其扩散活化能(Ea= 4.38 kJ/mol)最低,自扩散系数随温度的升高变化最慢。
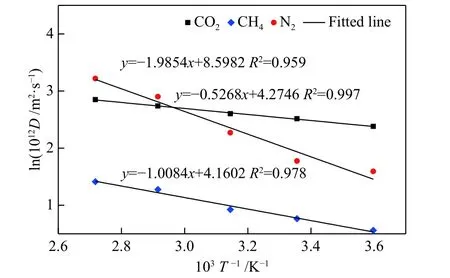
图9 CO2、CH4 和N2 在K-MER 型沸石中自扩散系数与温度的关系Figure 9 Temperature dependence of self-diffusion coefficients for CO2, CH4 and N2 on K-MER zeolites
2.3 渗透性质
为了考察K-MER 型沸石对混合气体的渗透率和选择性,采用MD 模拟了CO2/CH4、CO2/N2和N2/CH4体系的分离性能。气体通量即渗透率(F)是评价沸石膜的重要指标,通过统计随时间变化的渗透分子数量计算渗透率。在模拟中,进入侧室中的气体分子数记为N,随着时间(τ)的积累,侧室中气体分子数逐渐增加。在温度为298 K 下,不同分离体系渗透分子数与时间的关系如图10所示。根据文献[28],渗透分子数(N) 随时间(τ)的变化关系符合式(4):

图10 穿透分子数随时间的变化Figure 10 Number of permeation molecules versus time

式中,F为分子渗透率(mol/(s·m2·Pa)),Nal为沸石膜中吸附的分子数,常数150 和1.98 × 1012与气体初始时刻的分子数和压力有关。
根据式(4),对模拟得到的渗透分子数随时间的变化曲线进行拟合,分别得到了CO2/CH4、N2/CH4和CO2/N2分离体系中主要渗透分子CO2、N2和CO2的 渗 透 率 为5.56×10−6、9.88×10−6和9.23×10−6mol/(s·m2·Pa),即渗透率 ~104GPU(1 GPU = 3.35×10−10mol/(s·m2·Pa)),比传统聚合物分离膜(~100 GPU)提高了2 个数量级。Yeo 等[10]实验得到K-MER 型沸石膜对CO2/CH4分离体系中CO2的渗透率为6.2×10−7mol/(s·m2·Pa)。本文模拟值高于实验值,原因可能是实验制备的沸石膜厚度(~4.5 μm)明显大于模拟沸石膜的厚度。这也说明沸石膜的厚度是影响气体渗透率的重要因素。
选择性是分离膜的另一个重要指标,混合气体分离的选择性(s)定义为:

式中,x1、x2分别为气室中气体的摩尔组成,y1、y2分别为侧室中气体的摩尔组成。
图11 所示为混合气体经过5 ns 后气体分子在模拟盒子中的分布快照。可以看出,CO2/CH4混合气体在整个模拟时间内,CH4未能穿过沸石膜进入到侧室,只有CO2通过,说明K-MER 型沸石膜对CO2/CH4具有极高的分离选择性。但需要指出的是,CH4能够穿过K-MER 型沸石膜,其对CO2/CH4的选择性不是无穷大。Yeo 等[10]实验制备的K-MER型沸石膜对CO2/CH4的选择性为77.5。在本文N2/CH4分离体系的模拟中也可以观察CH4穿过了K-MER型沸石膜。造成这种现象的原因是受限于计算机的计算能力,模拟时间不是足够长。K-MER 型沸石膜对N2/CH4和CO2/N2分离体系的选择性分别为39 和24.7。上述结果表明,K-MER 型沸石膜对CO2/CH4、CO2/N2和N2/CH4体系均具有良好的分离选择性。

图11 MD 模拟5 ns 后混合气体穿过沸石膜的快照Figure 11 Snapshot of mixed gas permeating through zeolite membrane after a MD simulation time of 5 ns
3 结 论
采用GCMC 方法研究了CO2、CH4和N2在MER型沸石中吸附性能,模拟结果与实验结果吻合证明了模型和力场的可靠性。综合分析三种气体的吸附性能数据可知,MER 型沸石对吸附质的吸附量和吸附热的大小由沸石的结构、骨架外阳离子以及吸附质的性质等共同决定。
采用MD 模拟技术研究了CO2、CH4和N2在MER 型沸石中扩散和分离性能。研究结果如下:(1) CO2、CH4和N2在MER 型沸石中存在亚扩散现象,它们的扩散方式为构型扩散。气体分子在沸石三维通道中的扩散存在各向异性,在K-MER型沸石中气体分子优先向x轴方向扩散。沸石与气体之间的作用力和沸石骨架外阳离子均对气体的扩散能力有影响,而沸石骨架外阳离子是影响气体分子扩散能力的主要因素。(2) 在K-MER 型沸石中,CO2和N2的自扩散系数随吸附浓度的增加而减小;CH4的自扩散系数随着吸附浓度的增大先增加后减小。随着温度的升高,CO2、CH4和N2的自扩散系数均增加,扩散活化能大小顺序为N2(16.51 kJ/mol) > CH4(8.39 kJ/mol) > CO2(4.38 kJ/mol)。(3) K-MER 型沸石膜对CO2/CH4、CO2/N2和N2/CH4分离体系均具有良好的分离选择性,主要渗透分子的渗透率~104GPU(1 GPU = 3.35×10−10mol/(s·m2·Pa))。
猜你喜欢
杂志排行
燃料化学学报的其它文章
- Mo-Sn 催化剂上甲醇低温氧化制甲缩醛
- 酸活化蒙脱土在二甲醚水蒸气重整制氢中的应用
- Ni 对MoS2 基催化剂活性相及加氢脱氮脱硫性能的影响
- Insight into reaction path and mechanism of catalytic cracking of n-hexane in HZSM-5 zeolites
- Addition of bismuth to Pt and Pd for electric power generation with selective cogeneration of acetate from ethanol in a fuel cell type reactor
- 淖毛湖褐煤分级萃取可溶有机质的组成结构特征及萃余残渣的热转化性能
