一类非线性浅水波方程的对称动态分析和精确解
2021-11-20康晓蓉鲜大权鲜骊珠
康晓蓉,鲜大权,鲜骊珠
(1.西南科技大学理学院,四川 绵阳 621010;2.成都理工大学中英合作办学,四川 成都 610059)
非线性偏微分方程的孤子解由于可以提供有价值的信息来理解非线性物理现象而受到各个领域的广泛关注,如浅水波方程可以描述流体动力学、弹性介质和等离子体中的一些现象而被广泛应用于环境保护、海洋开发、灾害预防以及流体动力学等领域。通常,直接求解这些非线性方程的精确解是极其困难的,寻求有效的求解方法成为学者关注的重点。近年来已有很多具体方法,如exp(-φ(ξ))扩展方法[1]、G′/G展开法[2]、Riccati 方程辅助法[3]、tanh 展开法[4]、对称法[5]、同伦分析法[6]、反散射法[7]、CK 直接约化法[8]、CkdVE 方法[9]等被应用于求解多种孤子方程的精确解。
本文研究带有两个非零任意常系数的非线性浅水波方程:
其中a1,a2为任意非零常数。该方程包含了以下两个著名的非线性模型:
1)当a1=3,a2=-2时,方程(1)即为常用来描述浅水波在水平底面上单向、无旋传播状态的Camassa-Holm(CH)方程[10];许多学者对该方程的守恒律、适定性、几何结构等性质进行系统研究并推导出紧孤立波解、尖峰孤立波解、钟型孤波解等丰富的解。
2) 当a1=4,a2=-3时,方程(1)即为用于模拟弥散介质中非线性波动的Degasperis-Procesi(DP)方程[11],该方程同样在尖峰孤立波解和周期尖波解等解析解的研究方面取得富有成效的结果。
考虑到广义浅水波模型在物理应用上更具有普遍性,研究该方程的局部特征及精确的相互作用解是更有意义的工作,因此本文将利用Lie 群方法得到浅水波方程(1)的生成元和李代数,应用所得的Lie 对称约化方程,采用截断幂级数展开法寻求方程的精确解结构,并给出某些解的局域激发特征及几何结构分析。
1 浅水波方程的对称约化
根据Lie 群理论[12-13],浅水波方程(1)的Lie 点对称σ(x,y,t)满足如下方程:
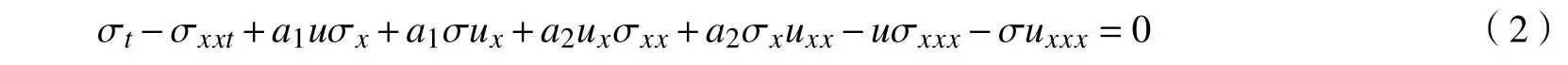
其中u=u(x,t)满足浅水波方程(1)。假设 σ具有形式:

其中d,e,f,g为关于变量x,t的待定函数,u=u(x,t)满足方程(1)。将式(3)代入式(2),得到d,e,f,g及u满足的多项式:
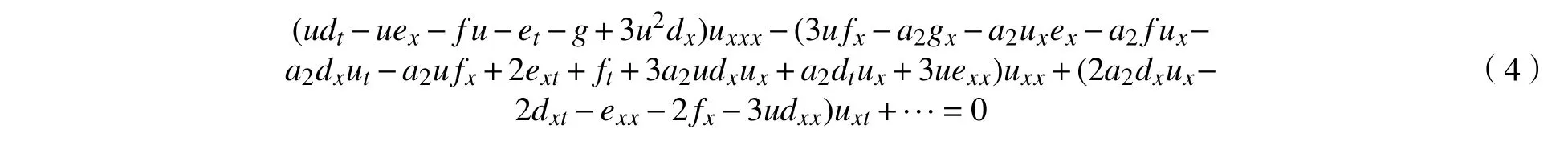
由未知函数u与其各阶导数的线性无关性,有
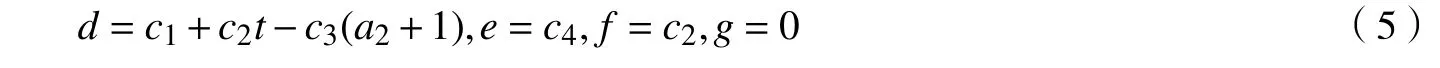
其中c1∈R,c2,c3,c4为非零实数。将(5)式代入(3)式得浅水波方程(1)的Lie 点对称:
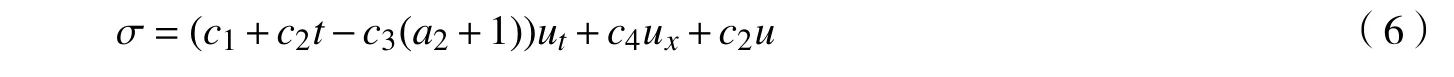
求解基于对称(6)的线性偏微分方程σ=0,可得:
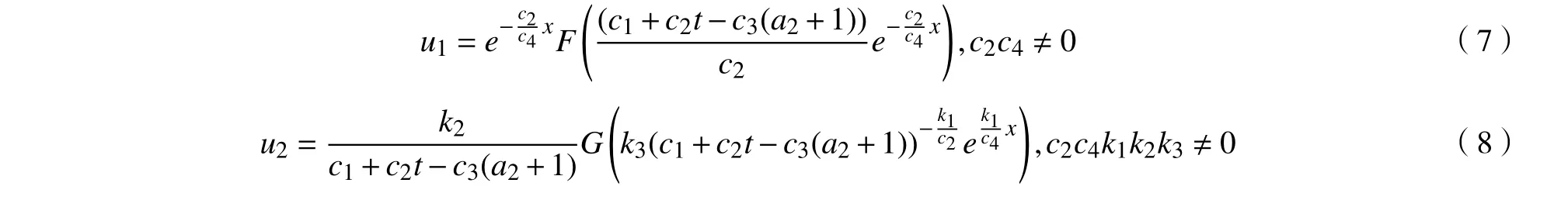
其中F,G均为一元可微函数。
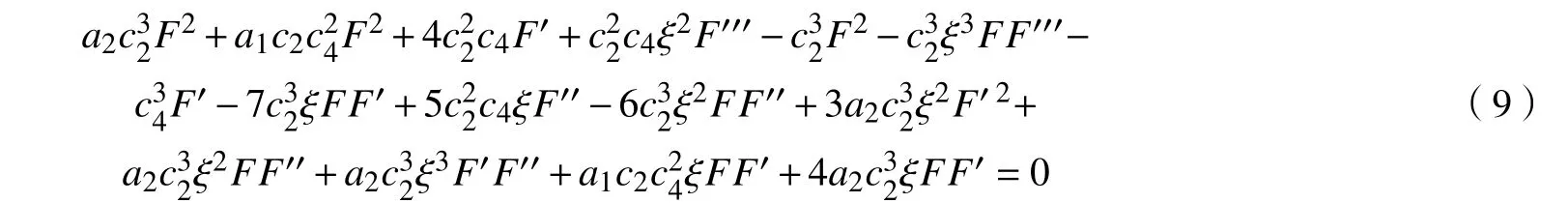
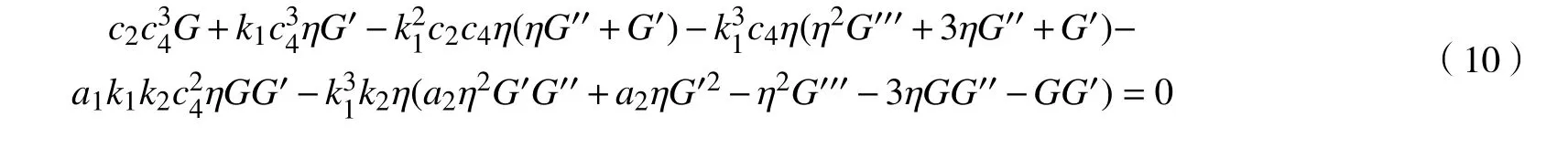
2 约化方程(9)和方程(10)的解
假设方程(9)具有变换F(ξ)=b1ξ+b2ξ2+b3ξ3+b4ξ4+b5ξ5,其中bi(i=1,···,5)为不全为零的待定参数,利用截断幂级数展开法[14-15],得到关于待定参数的非线性超定代数方程组:
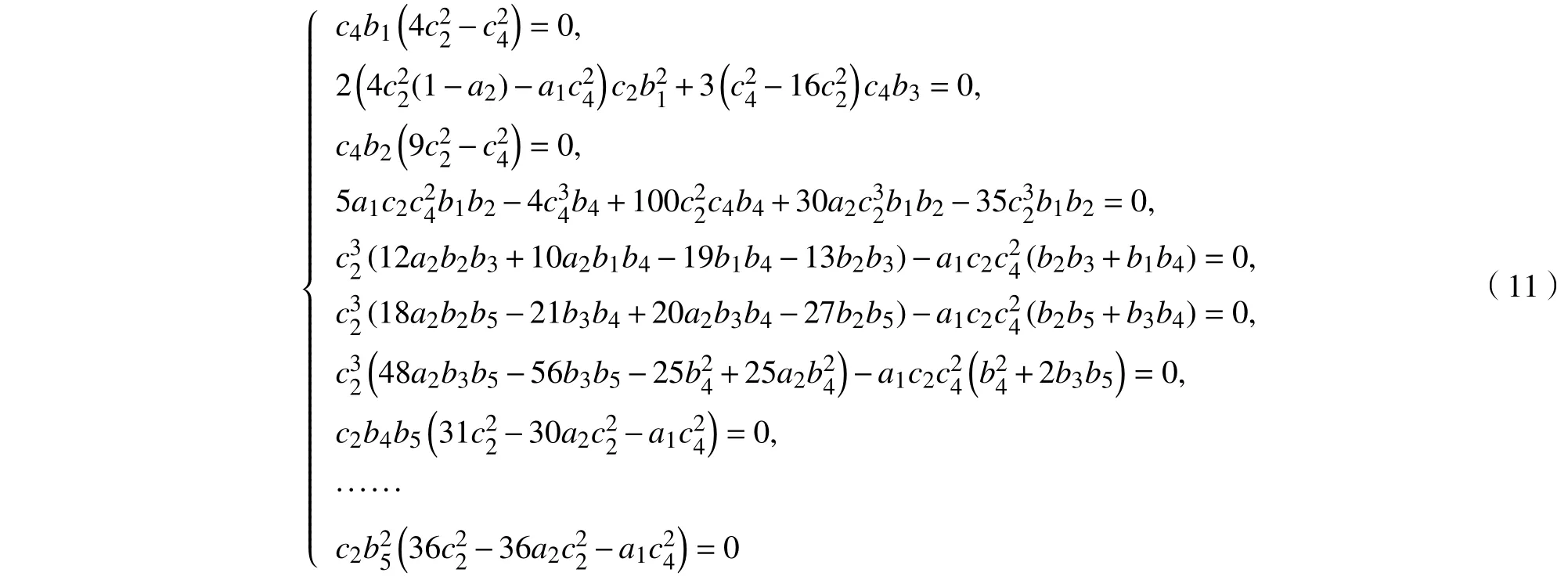
根据系统(11)的解可得方程(9)的解F1(ξ)和F2(ξ):
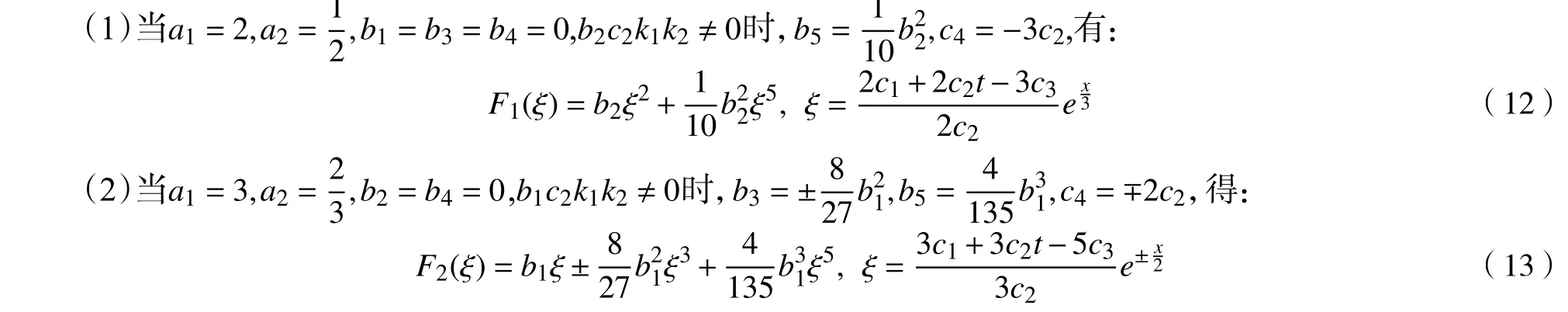
设方程(10)有变换G(η)=b1η+b2η2+b3η3+b4η4+b5η5+b6η6,类似地可得到方程组:
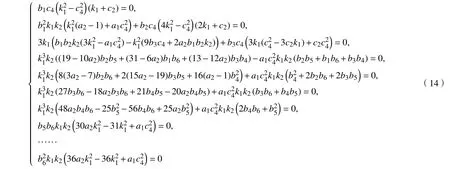
由系统(14)的解得到方程(10)的解G1(ξ)~G5(ξ)如下:
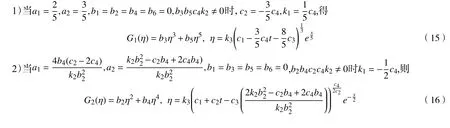
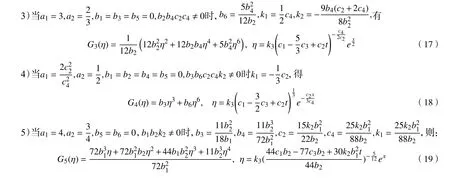
3 浅水波方程(1)的新非行波解结构及局域演化特征
将式(12)—式(13)分别代入式(7),将式(15)—式(19)分别代入式(8),可得浅水波方程(1)的一系列解如下:

下面以u7(x,t)为代表,讨论浅水波方程(1)的非行波局域演化特征及几何结构。

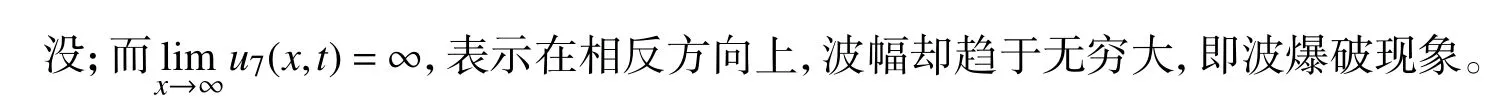
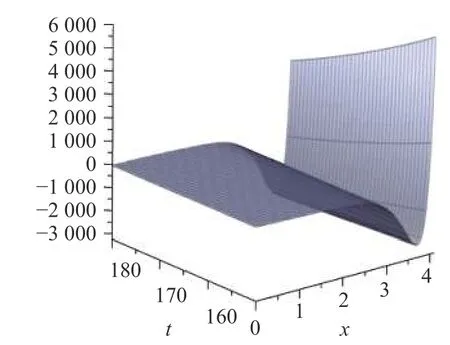
图1 参数I 下u7(x,t)的局域几何结构
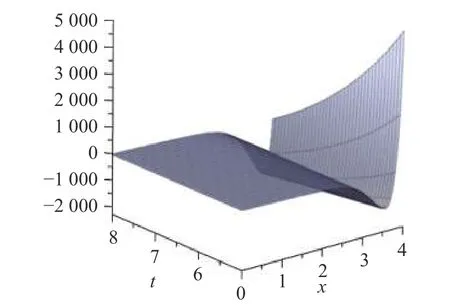
图2 参数II 下u7(x,t)的局域几何结构
4 结论
本文运用李群法得到非线性浅水波方程(1)的两个Lie 点对称约化,应用截断幂级数展开法得到了约化方程的解,获得方程(1)新的非行波精确解结构。以精确解u7(x,t)为代表讨论了方程(1)解的局域演化特征及其几何结构。这些结果不但丰富了非线性浅水波方程的可积意义和解的类型,并且对进一步研究同类模型具有较高的参考价值。
