广义BBM-KdV 方程的两种孤波解及其守恒律
2021-11-20胡劲松
王 希,傅 浈,胡劲松
(西华大学理学院,四川 成都 610039)
非线性发展方程是众多偏微分方程中一类重要的方程,可利用非线性发展方程刻画许多不同类型的物理模型,包括原子物理、等离子物理、固态物理、可压缩材料物理、光纤、流体力学、弹性介质、统计算法、生物学、地球化学等中观察到的波现象[1-14]。寻找非线性发展方程的显示解析解是众多数学家、物理学家们长期以来一直重点关注的一个问题,并在许多自然科学和工程领域中有着广泛的应用。目前,求某些非线性发展方程的精确(行波)解一般都是将方程改写成多变量或特殊函数的多项式形式,从而化简为一个更简单的方程再求解,如双曲函数展开法、Backlund 变换法、Jacobi 椭圆函数展开法、分离变量法、Sine-Cosine展开法、He’s 变分原理、Lie 对称方法等[12-18]。
本文讨论如下一类广义BBM-KdV 方程
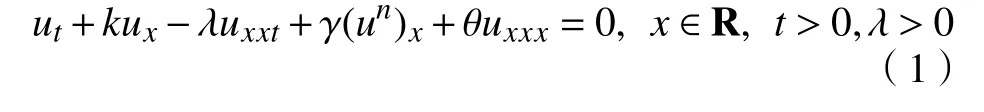
(k,λ,γ,θ均为常数,n≥2是正整数)的孤波解。特别地,当n=2时,方程(1)即为通常的BBM-KdV方程。
当θ=0时,方程(1)即为广义Benjamin-Bona-Mahoney(BBM)方程,也被称为正则长波(RLW)方程:
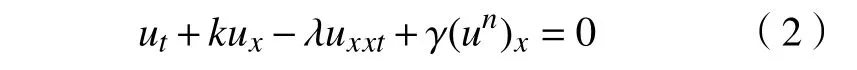
当λ=0时,方程(1)即为著名的Korteweg de Vries(KdV)方程[3,14]:
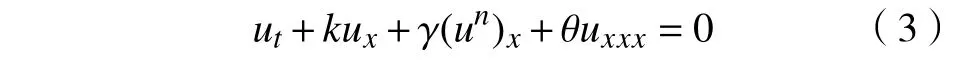
BBM 方程(2)和KdV 方程(3)都是弱非线性色散介质中长波单向传播的重要模型,它们都有稳定的孤波解。BBM-KdV 方程是BBM 方程和KdV 方程的推广形式,文献[19]对广义BBM-KdV方程(1)给出了两个物理守恒量,但并未给出严格的理论证明。本文将首先给出广义BBM-KdV 方程(1)两个物理守恒量的理论证明,然后用ansätze 方法[20-21],分别给出其双曲正割形式孤波解和双曲余割形式孤波解。
1 方程(1)的守恒量
由于广义BBM-KdV 方程(1)的物理边界满足:
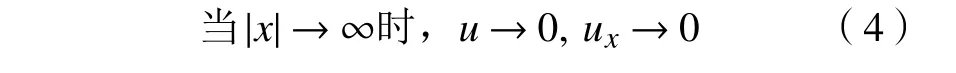
于是关于广义BBM-KdV 方程(1)的守恒性质有如下结论:
定理1广义BBM-KdV 方程(1)具有如下两个物理守恒量(t>0):
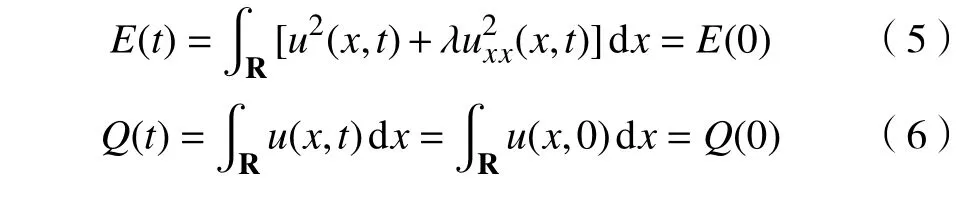
证明:由方程(1)得
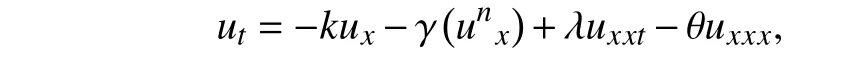
于是,有
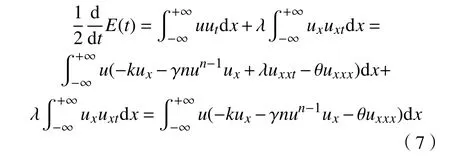
结合边界条件(4)分别有:
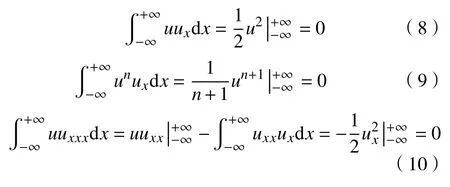
2 方程(1)的双曲正割孤波解
定理2方程(1)有如下形式的孤波解:
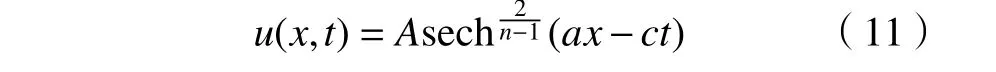
这里a、c、A是常数,且满足:
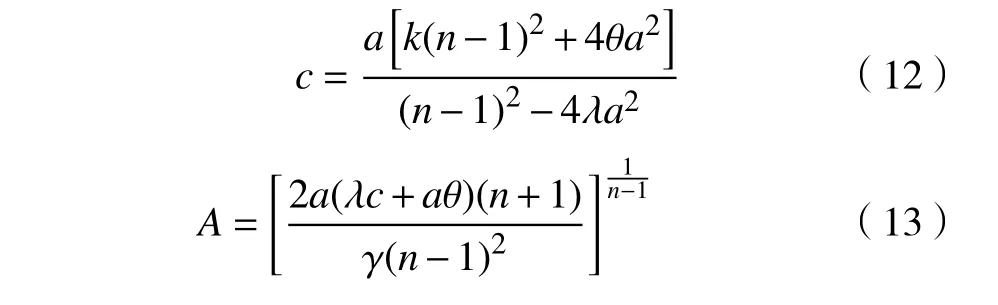
证明:对广义BBM-KdV 方程(1)考虑双曲正割-ansätze 方法,假设方程(1)的孤波解为:
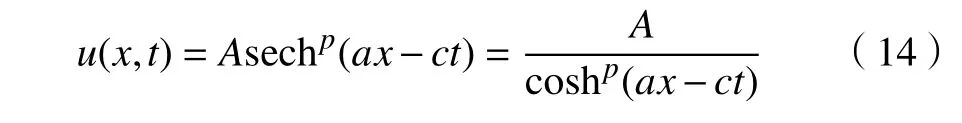
其中,A,a,c为待定常数;为方便后面的讨论,简记

将式(15)—式(19)代入方程(1),得

令pn=p+2,则

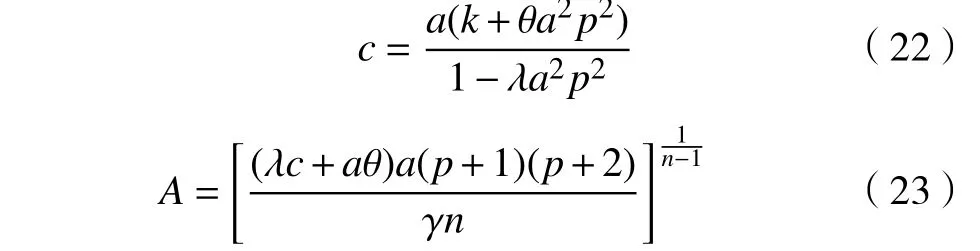
将式(21)代入式(22)、式(23),即有式(12)、式(13),从而得到广义BBM-KdV 方程(1)的双曲正割孤波解为(11)。
3 方程(1)的双曲余割孤波解
定理3方程(1)有如下形式的孤波解:
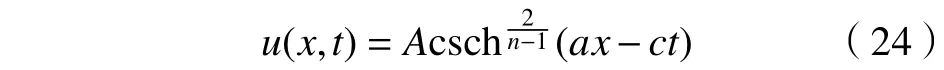
这里a、c、A是常数,且满足:
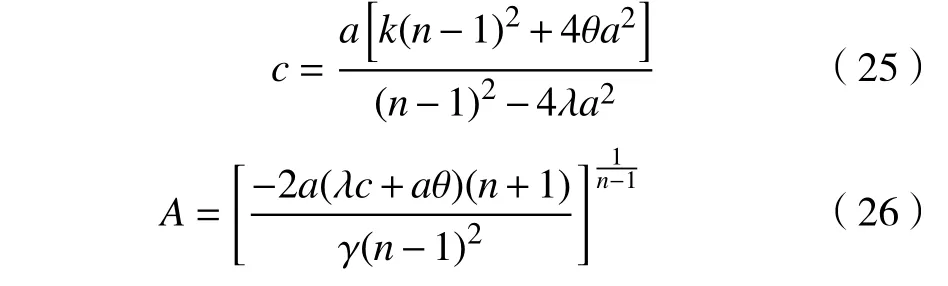
证明:对广义BBM-KdV 方程(1)考虑双曲余割-ansätze 方法,假设方程(1)的孤波解为:
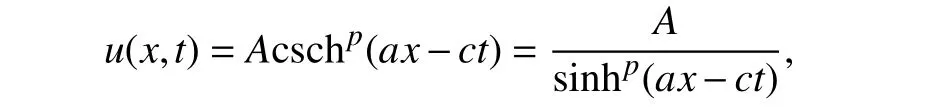
其中,A、a、c为待定常数。则有

将式(27)—式(31)代入方程(1),得

令pn=p+2,则

将式(33)式代入式(34)、式(35),即有式(25)、式(26),从而得到广义BBM-KdV 方程(1)的双曲余割孤波解为(24)。
4 结束语
本文用最有效最直接的ansätze 方法构造了广义BBM-KdV 方程(1)的两种不同形式的孤波解,从定理2 和定理3 可以看出,只需要给定一个常数a,就可以确定常数c和A,从而到广义BBM-KdV 方程(1)的双曲正割形式孤波解(11)或双曲余割形式孤波解(24)。同时也进一步验证广义BBMKdV 方程(1)所满足的物理边界条件(4)。
