LF 精炼工艺中钢包底吹氩过程数值模拟
2021-11-20唐祁峰尹仕伟刘庭耀彭必友
唐祁峰,尹仕伟,黄 华,杨 韬,张 军,王 宇,刘庭耀,彭必友
(1.西华大学材料科学与工程学院,四川 成都 610039;2.攀钢集团攀枝花钢铁研究院有限公司,四川 攀枝花 617000;3.攀钢集团江油长城特殊钢有限公司,四川 江油 621701;4.西华大学机械工程学院,四川 成都 610039)
钢中的脱硫、脱氧、去除杂质、合金化等很多环节均能通过LF 炉精炼完成[1-3]。在LF 炉精炼时,采用钢包吹氩来搅动钢液,能加速液相传质速率,快速均匀温度,促进渣金界面反应和钢中夹杂迅速上浮,是提升钢洁净度的重要手段[4-6]。在精炼吹氩工艺中,吹氩的方式、位置、角度以及流量都对吹氩搅拌效果有着极为重要的影响。在钢铁冶炼时,其过程极为复杂,试验对设备要求高,原料成本大。而随着CAE 技术的发展,利用数值模拟方法来研究冶金工程中的复杂问题,能显著地节约时间和试验成分,越来越受到了人们的重视[7-8]。娄文涛等[9]研究了钢包底吹氩过程对渣金反应的影响,获得了吹氩流量对钢液脱硫的影响规律。Ajmani 等[10]讨论了在采用顶吹方式中,吹气孔尺寸与混匀时间之间的关系。蒋星亮等[11]采用数值模拟和水模型物理模拟,对比了钢包底单吹和双吹对钢液“死区”的影响。诸如此类关于钢包吹氩数值模拟的研究还有很多,说明采用CAE 技术进行数值模拟是一种分析钢包吹氩精炼过程的有效手段。
为了节约现场试验时间和成本,促进生产顺利进行,本文拟采用专业的CFD 流体工程软件FLUENT 对LF 炉精炼过程中钢包底单孔偏心垂直吹氩过程进行数值模拟,探讨底吹气体流量对LF 炉炼钢过程中熔池内熔体流动速度以及钢液“死区”的影响。结果发现,采用偏心底吹,当氩气流量到达一定值时,会在钢液内部形成一个闭合的气循环区域,使“死区”面积显著下降。通过对比湍动能、流速和钢液“死区”比例,获取了最佳的模拟吹氩流量。
1 数学模型
欧拉-欧拉(Euler-Euler)模型可以模拟各相之间的作用力,准确反应气体气泡群在流体中的行为,且计算过程采用欧拉-欧拉模型模拟所占用的计算机CPU 资源较少,因此被广泛应用于气液两相流模拟中[12-13]。为了探讨底吹气体流量对LF炉炼钢过程中熔池内熔体流动速度的影响,本文在CFD 模型建立过程中引入了欧拉-欧拉模型。
在模拟之前,首先提出了以下基本假设条件:钢包中的钢液上方不存在熔融炉渣;钢液为不可压缩的牛顿流体,且不考虑温度变化;假设气相为刚性球,具有不可压缩性,且不受温度影响;气相浮力是液相流动的驱动力;钢液上表面是水平的,不存在液面波动。
LF 炉中的流体处于湍流状态,系统应遵循以下控制方程[14-16]。
1)质量守恒方程
连续性方程是质量守恒定律在运动流体中的数学表达式,认为等温条件下两相流之间不存在质量传递,则由微元体的质量守恒可导出流体的连续性方程。其相关的方程可以表示为
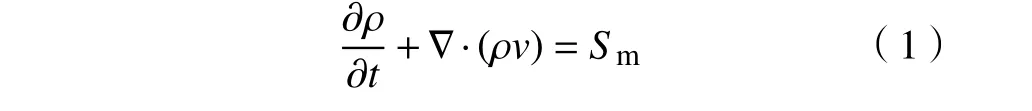
式中:ρ为流体密度,kg/m3;v为流体速度,m/s;Sm为加入连续相的质量,kg;t为时间,s。
2)动量守恒方程
根据牛顿第二定律,动量守恒定律表述为:微元体中流体的动量对时间的变化率等于外界作用在该微元体上的各种力之和,其表达式为
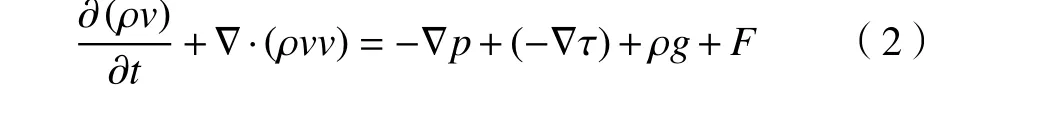
式中:p为静压力,MPa;g为体积力,N;F为其他外部的体积力,N;τ为黏性应力张量。
3) 能量守恒方程
根据热力学第一定律,能量守恒定律表述为:微元体中能量的增加率等于进入微元体的净热流量加上体力与面力对微元体所做的功,其表达式为
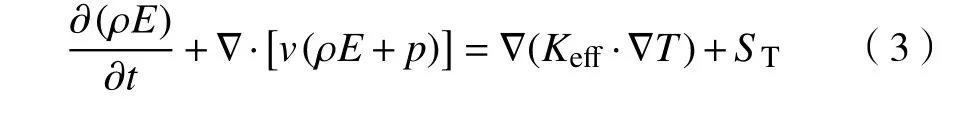
式中:E为微元体流体的总能,即内能和动能之和,J;Keff为有效导热系数,W/(m·K);T为温度,K;ST为由于化学反应引起的放热和吸热,或其他自定义的热源项,J。
4)湍流控制方程
本文采用标准k-ε模型,其湍流动能k方程及湍流耗散率 ε方程分别由式(4)和式(5)来表示:
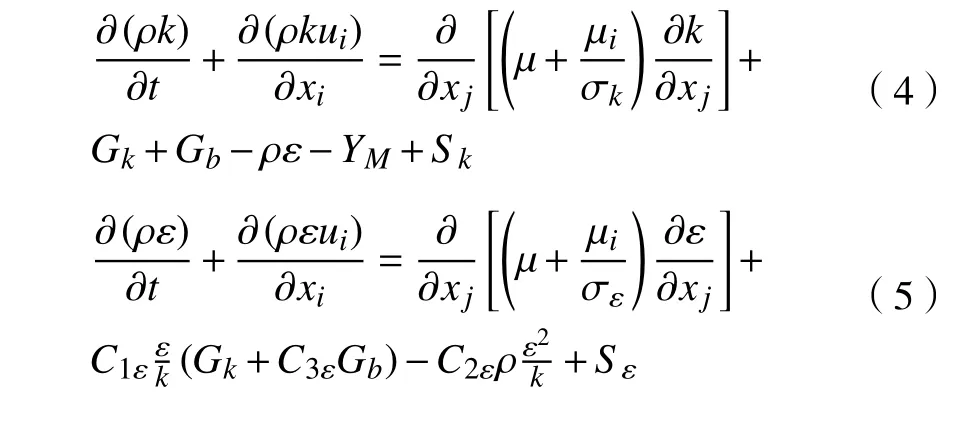
式中:Gk是平均速度梯度引起的湍动能,m2/s2;Gb是由浮力产生的湍流动能,m2/s2;C1ε、C2ε、C3ε为经验常数,分别取值1.44、1.92、0.1;σk、σε分别为湍动能和耗散率对应的普朗特数,分别取值1.0、1.0;YM为可压湍流脉动膨胀对总耗散率的影响。
2 数值模拟结果与分析
LF 炉钢包的结构示意图如图1(a) 所示,其具体参数见表1。从图1 中可以看出钢包呈有轻微锥度的圆柱体状,钢包顶直径为2 440 mm,底直径为2 234 mm,熔池深度为2 127 mm,钢包锥度为3°,大约能容纳70 t 左右的钢水。该钢包采用单喷嘴垂直吹氩,通气砖位于钢包底部1/3R偏心位置,底吹孔直径为105 mm。根据钢包形状,利用CAE 分析软件FLUENT 建立有限元模型,模型采用六面体网格进行划分,其示意图见图1(b)。

图1 钢包结构与有限元模型

表1 钢包结构参数
模型的基本假设和流体的边界条件设置如下:模型不考虑传热,且假设初始状态时钢液是静止的,钢液上表面渣层的影响忽略不计;在钢包和通气管壁处,不考虑滑移边界条件,并采用了壁面函数处理;钢包底面的喷嘴管处作为氩气流的速度入口,钢液顶部作为压力出口。
图2 是典型吹氩量为30 Nm3/h 时,不同时间下气流场的分布图。从图2(a)中可以看出,在刚开始吹氩1 s 时间内,氩气由透气砖进入熔池内,钢包底部形成一个短小的垂直气柱。气柱内部气体流速较高,外部因气体在液体中扩散受阻,动力不足,流速逐渐下降。随吹氩时间延长,气体受浮力的作用,垂直向上运动,且在上方因扩散对流形成了两个小的气流循环区域。两个循环区域随吹氩时间延长逐渐开始分化,吹氩孔所在一侧的气流扩散受阻于钢包壁,而另一侧的气流扩散空间较大,从而形成了一大一小两个循环,且气柱逐渐向钢包壁偏移(图2(c))。进一步延长吹氩时间,气柱朝钢包壁偏移程度加剧,大的气流循环区域不断压缩小的气流循环区域空间。从图2(f)中可以观察到,当吹氩时间为21 s 时,气流几乎是沿着钢包壁流动,经钢液上层,再扩散至钢包另一侧,然后进一步流动至钢包底部,最终在整个熔池内形成一个接近于闭合的区域,说明在该吹气参数下,熔池的混匀时间大约在20 s 左右。
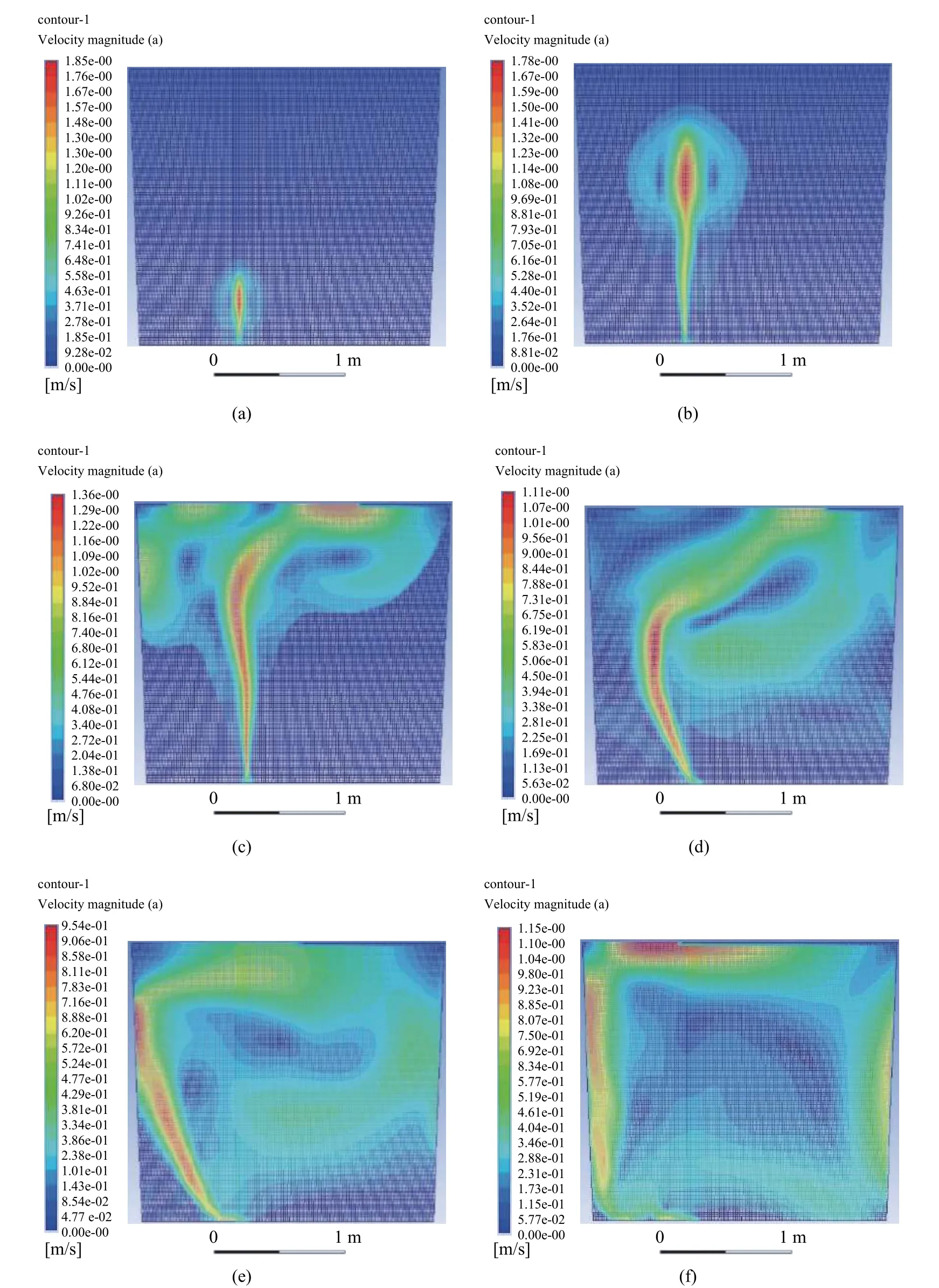
图2 不同时间炉内流场分布
氩气在钢液内流动,能有效地搅拌钢液,使钢液中的夹杂迅速上浮,加速渣金界面反应,起到很好的精炼效果。氩气在钢液中的搅拌强度和有效搅拌区域与气流的速度和动能有关,而这两者又在一定程度上取决于单位时间内的吹气量。图3 是不同吹气量下,钢包内流体的平均湍动能和平均速度的变化规律。从图中可以看出,随着单位吹气量的增加,平均湍动能和平均速度均呈上升趋势。吹气量为10 Nm3/h,吹气量小,平均湍动能和平均速度也较小,其值分别为2.8 m2/s2和0.036 m/s。加大吹气量,进入钢液的氩气压力增加,使平均湍动能和平均速度迅速增大。当吹气量加大至30 Nm3/h,平均湍动能和平均速度分别达到6.2 m2/s2和0.073 m/s,两者的值较吹气量为10 Nm3/h 时均增大了一倍以上。在此基础上,进一步加大吹气量,虽然平均湍动能和平均速度会进一步增大,但增大幅度减缓。对比吹气量为50 Nm3/h 和30 Nm3/h,平均湍动能提升约30%,而平均速度仅提升约15%。这说明当吹气量达到某一临界值时,进一步加大吹气量,平均湍动能和平均速度提升有限,反而会使氩气利用率降低。

图3 平均湍动能和平均速度随吹气量的变化曲线
平均湍动能和平均速度之所以在大吹气量下提升有限,这和钢液中存在流动速度几乎接近于零的“死区”有关。图4 为不同吹气量下熔池内速度小于0.02 m/s 的区域与整个熔池区域的比值。低吹气量时,加大吹气量会使死区的比例显著下降;高吹气量下,加大吹气量死区比例趋于稳定。当吹气量低时,气流的动能较小,能到达的区域也较小,所以使钢液中存在大量的死区。随着吹气量加大,会使气流获得更大的动能,能扩散的区域增大,从而减少死区面积。图5 为吹氩流量10 Nm3/h 和20 Nm3/h 时稳定状态下的气体流场分布。从图中可以看出,这两个吹气量下,气流的动能不足,没有形成完整的大的气流循环区域,导致死区面积较大。当吹气量从10 Nm3/h 加大到20 Nm3/h 时,气流的动能有所提高,能扩散的区域增大,死区比例从21%下降到13%。加大吹气量至30 Nm3/h 时,气流所获得的动能也再次明显增大,最终使气流在钢包内部形成了闭合的气流圈(见图2(f)),从而导致死区比例下降到6%。再进一步加大吹气量至40 Nm3/h 和50 Nm3/h 时,钢液死区比例几乎无变化,而是趋向稳定。这是由于在高吹气量下,钢液中已经形成了相对闭合的气流圈。加大吹气量,虽然可以使气流获得更大的动能和速度,但不会使气体流向闭合圈内的区域,从而无法对该区域的钢液起到搅拌作用,导致死区比例不会进一步下降。
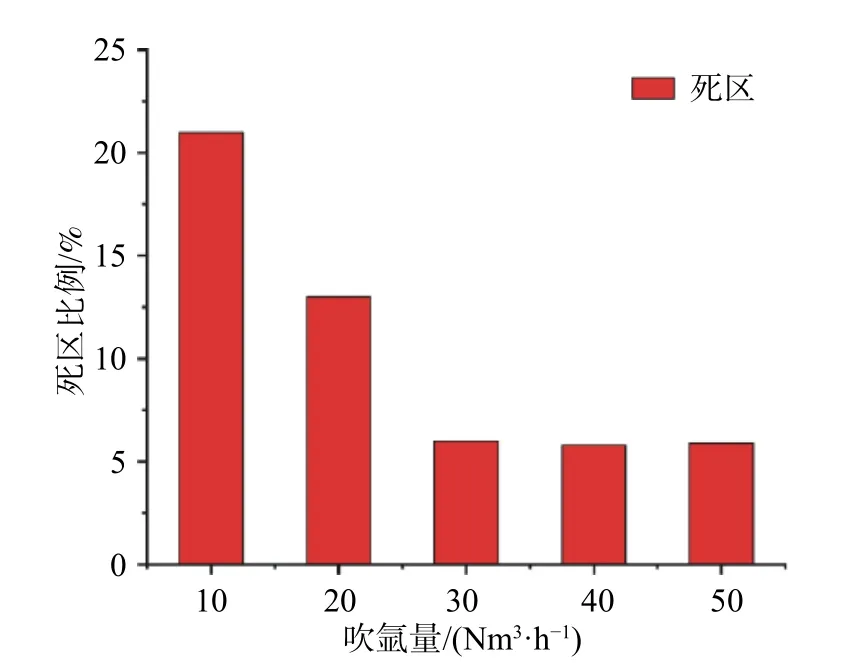
图4 死区比例随吹气量的变化情况
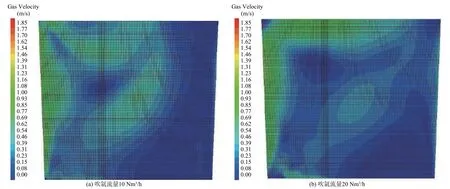
图5 吹氩流量10 Nm3/h 和20 Nm3/h 时的气体流场分布
综合分析上述模拟结果,得出本文的吹氩量在30 Nm3/h 左右较为合理。在该参数下,钢液中的流体能够获得较大的平均湍动能和平均速度,且钢液中死区比例也达到最小,使钢液获得了较大的搅拌强度和搅拌区域。
3 结论
本文对LF 炉精炼工艺中钢包单孔偏心底垂直吹氩过程进行了数值模拟分析,得出以下结论。
1)吹氩流量为30 Nm3/h 时,随吹氩时间的推移,气流最终会形成一个分布在钢液边缘的闭合循环区域。
2)吹气量的临界值为30 Nm3/h。低于临界值时,平均湍动能和平均速度随着吹氩流量增大而显著增大;高于临界值,平均动能和平均速度增速缓慢。
3)在吹氩过程中,钢液中存在流动缓慢的死区。吹气量从10 Nm3/h 加大至30 Nm3/h 的过程中,死区比例从21%降至6%,减小明显。进一步加大吹气量,死区比例几乎没有变化,反而氩气利用率降低。本模拟过程中的最佳吹气量为30 Nm3/h。
