基于热-流耦合模型研究激光熔覆速度场影响机制

赵明娟，李宝星, 吴 涛，赵龙志，曾建邦，焦海涛，李 劲，宋立军,4

（1. 华东交通大学载运工具先进材料与激光增材制造南昌市重点实验室，江西 南昌 330013；2. 华东交通大学轨道交通基础设施性能监测与保障国家重点实验室，江西 南昌 330013；3. 南昌铁路局通达工贸有限责任公司，江西 南昌 330002； 4. 湖南大学机械与运载工程学院，湖南 长沙 410082）

激光熔覆工艺具有激光能量密度高、加工过程急热快冷、熔覆层界面结合强等显著特点，常用来制备服役寿命长、高耐磨耐腐蚀的熔覆层，在材料表面强化和关键部件的再制造领域具有广阔的应用前景[1]。 工艺参数（如激光功率、光斑半径、扫描速度和送粉率等）的设置会极大影响熔覆过程中熔池的温度场、速度场和涂层应力场的分布，从而决定熔覆层中相的构成、形态和分布，并对熔覆层的服役性能造成重要影响[2-3]。 选择合理的工艺参数和调节熔池内温度梯度及分布是提升熔覆层质量的重要途径。 但是，现有设备难以对熔覆层内温度场和速度场分布进行实时的精确监测，单一的实验研究又会耗费大量物力人力，且周期较长，这也大大限制了人们对激光工艺参数与涂层性能关联性的有效研究。

随着计算机科学技术的快速发展，计算机技术的模拟运算能力得到极大的提升，从而大大减少了激光熔覆过程的模拟计算时间，同时也提高了计算结果的准确性。 因而应用模拟仿真技术研究激光熔覆过程有利于人们深入理解激光熔覆机理，有利于制备出高质量的熔覆层[4-5]。

研究激光熔覆过程的现有数值模型主要有两大类：一类是热模型，该模型大多侧重于研究熔覆过程中的温度场分布，通过调整单一工艺参数（如激光功率、光斑半径、扫描速度和送粉率等）对激光熔覆过程中的温度、温度梯度分布及熔覆层形貌的影响[6-7]，但此类模型仅考虑了固体传热，忽略了固液相变和熔池内流体对流换热的影响。 另一类是热-流耦合模型， 此类模型不仅耦合了固体传热和流体流动，而且还考虑了固-液相变问题，因而这类模型可以更加精准地描述激光熔覆过程中所发生的物理冶金现象。 目前模拟仿真在激光熔覆过程的研究中具有广泛的应用，然而，研究人员并未系统地阐述激光工艺对激光熔覆过程中熔池内速度场的影响，不能全面理解熔池的演变过程[8-14]。 本文利用COMSOL 有限元软件建立了激光熔覆多物理场模型，模拟了熔池内温度场和速度场的分布，采用模拟和实验相结合的方法，不仅研究了激光熔覆过程中激光功率、光斑半径、扫描速度、送粉率等工艺参数对熔池内温度及流速分布的影响，同时模拟了不同材料表面张力系数下熔池温度场和速度场的分布状况，对激光熔覆工艺的优化具有一定的理论价值。

1 模型构建

1.1 数学模型

本文主要探讨激光工艺对熔池内温度场和速度场的影响，对激光熔覆过程的物理模型进行简化（图1），并作如下假设：

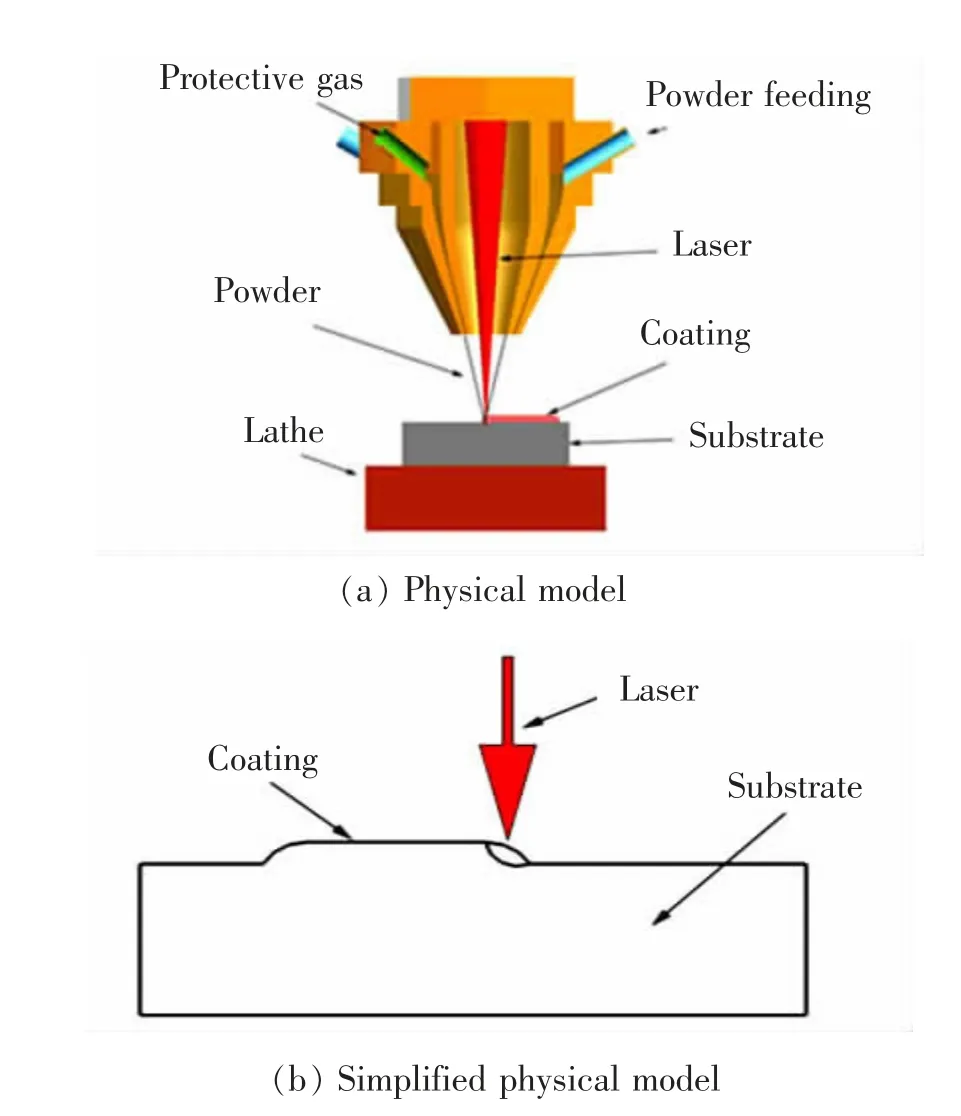
图1 激光熔覆物理模型Fig.1 Laser cladding physical model

1） 熔池流体为牛顿不可压缩的层流流体；

2） 材料的热物性参数不随温度变化，但材料的比热、粘度除外，同时考虑表面张力和相变潜热；

3） 熔池流体受热浮力与重力作用， 并符合Boussinesq 假设；

4） 激光热源呈高斯分布。

以上假设可得出熔池内流体必然遵守质量、能量和动量守恒方程，由此得出以下的控制方程。

（1） 质量守恒方程。 熔覆材料受热， 会发生固-液相变现象， 熔池内流体的质量必须守恒，方程如下

式中：F源项中第一项是流体热浮力与重力项； 第二项是达西源项；I 为相变潜热，kJ/mol；μ 为流体动力粘度系数；β 为材料热膨胀系数；T 为热力学温度，K；Tm为材料熔点，K；K 为某一常数；B 为避免分母为零的常数，此处设定为0.001；fl为液相体积分数。

（3） 能量守恒方程。 系统所遵守的能量守恒方程[16]为

式中：P 为激光功率，W；rb为光斑半径，mm；α 为激光吸收率；β 为粉末流对激光的遮蔽率。将上式绘制成图片，如图2 所示，从图中看出热源的能量密度呈中心高周边低的轴对称高斯分布。

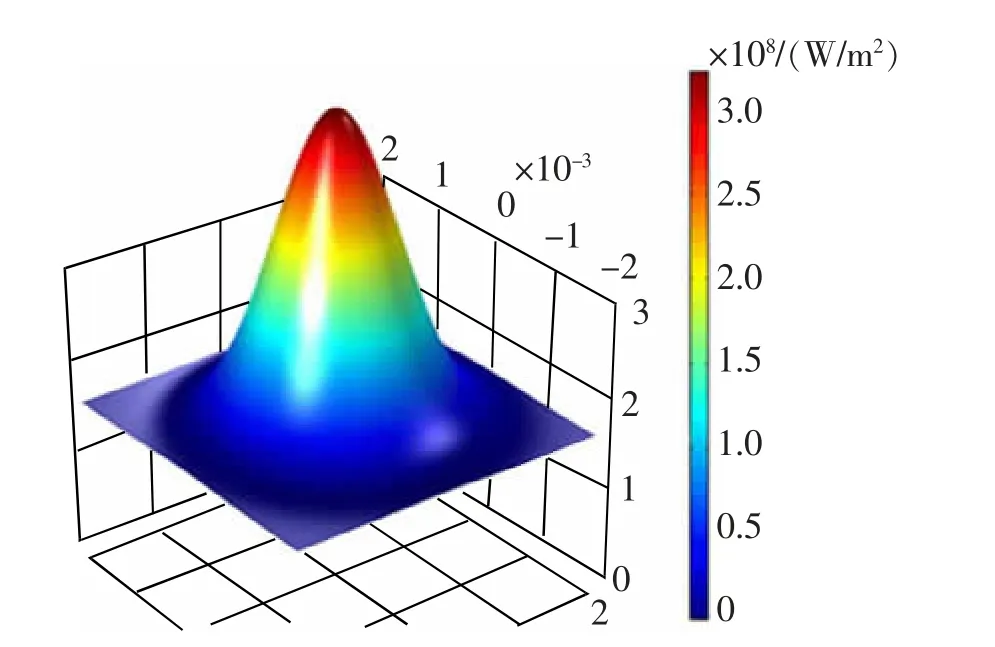
图2 高斯热源能量密度分布示意图Fig.2 Schematic diagram of Gauss energy density distribution

1.2 边界处理

将激光熔池内固相与液相之间的瞬间转化过程看作是多孔介质孔隙率的变化过程，其中液相在熔池所占比例按照平均分布的方式表示

式中：γ 为表面张力，N/m；u 和v 均为流体速度，m/s；g 是换热系数；σ 是玻尔兹曼常数；ε 是辐射率。

1.3 数值模型

借助COMSOL 仿真软件提供的流体传热模块，开发激光熔覆过程的热-流耦合模型。 模型计算区域尺寸为100 mm×10 mm， 为保证计算准确度和合理运算时间，本文网格采用自由三角形网格，同时对整体网格进行区别划分，温度和流速变化剧烈的部分采用极细网格，其余部分采用细网格。 其网格划分区域和边界条件如图3 所示。

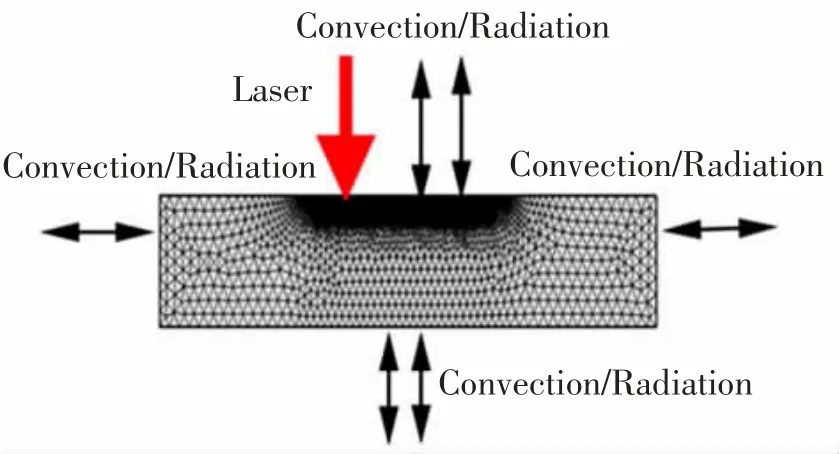
图3 网格剖分及边界条件Fig.3 Mesh division and boundary conditions

为了模拟出激光熔覆过程中不同阶段熔覆层外观形貌尺寸的变化， 本文利用COMSOL 软件中自带ALE（Arbitrary lagrangian-euleian）的移动网格功能进行模拟，熔覆层界面移动速度公式如下[17-19]

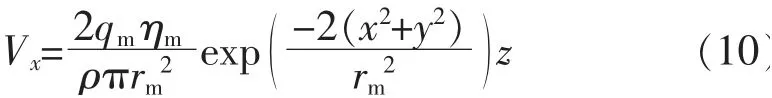
式中：qm为粉末质量流率，g/min；ηm为粉末捕获率；rm是粉末流半径，mm。

1.4 实验验证

模型计算的初始温度为室温， 激光功率为800 W， 激光束半径为2 mm, 送粉率为6 g/min，扫描速度为5 mm/s，基板为45 钢，粉末物性参数与基板一致。 与模拟相同的实验参数在10 mm 厚度的45 钢基板上制备激光熔覆涂层， 并对激光熔覆涂层横截面模型计算结果与实验结果进行对比（图4）。从图4 可以看出，实验与模拟所得到的熔覆涂层形貌尺寸结果较为吻合。

图4 熔覆层的横截面尺寸实验与模拟结果对比示意图Fig.4 Schematic diagram of cross-sectional dimension comparison between experiment and simulation results of cladding layer

为进一步验证模型的正确性，本文还探讨了送粉速率和激光功率的改变对熔池深度（h）和宽度（l）的影响，并与实验结果进行对比（图5）。 如图5 所示，激光功率对熔覆层尺寸影响的实验结果与仿真结果的误差在10%以内，这是因为激光功率的增加使得系统单位时间内接受的能量更多，能量输入的增加会扩大熔池的成形区域，从而加大了熔覆层的尺寸。 送粉率的实验与仿真吻合度在80%左右，这是由于仿真模型不考虑粉末流的遮蔽作用对系统能量的影响。 模型中单位时间内系统获得的能量输入不变，因而熔池的成形区域不会扩大，但熔池中心区域温度高，随着送粉率的增加，熔池中心所能获得熔化累积的熔体更多，熔覆层高度增加而宽度变化不大。

图5 工艺参数对熔覆层横截面尺寸的影响Fig.5 Effect of process parameters on the size of cross section sizes of laser cladding layer

2 仿真结果与分析

2.1 激光功率的影响

图6 分 别 是740，800，860 W 条 件 下 温 度 场和速度场分布， 图中颜色表示温度和速度的大小，箭头表示速度方向。由图6（a），图6（b），图6（c）可知，熔池中心温度最高，这是由于激光热源呈高斯分布，输出光源中间温度最高，并且激光功率增加，热输入量随着增大，熔池温度亦随着上升。由图6（d），图6（e），图6（f）可知，熔池表面流动的主要原因是由于温度梯度而形成的表面张力梯度， 表面张力大的流体对表面张力小的流体具有拉力作用，使得熔体从表面张力小的区域流向表面张力大的区域，即形成了Marangoni 效应[20-21]。 熔池内部流动则由浮力和重力共同作用下形成，熔池内熔体最高流速主要出现在熔池表面边缘处。图7 为熔覆过程中熔池内部最大流速在不同激光功率下的变化曲线，由图7 可知，在激光熔覆开始初期，熔体内部流速峰值较小，当熔覆至第2 s时， 熔体流速峰值快速上升至某一值并趋于平稳。 当熔覆至第6 s 时，第1 层熔覆完成，激光返回初始点并在第1 层熔覆层上进行第2 层熔覆，而第1 层熔覆层初始点处保留了热源一部分热量， 从而使得熔池内部熔体流速峰值出现剧增。然而，随着激光熔覆的持续进行，激光输入能量逐渐增多，熔池内部温度梯度较小。 从而熔体流速峰值缓慢降低。 当激光返回初始点在第2 层熔覆层进行第3 层熔覆时，熔池内熔体流速峰值再次快速上升，流速峰值最高可达到0.23 m/s，然后再缓慢降低，同时熔体流速峰值的下降幅度逐渐变小。 同时随着激光功率的上升，熔池流速峰值均会不断上升，同时激光功率的上升使得流速下降幅度逐渐缩小。 这是由于进行多层熔覆时，激光能量持续输入熔池，而单位时间熔池与外界环境的热量交换有限，熔覆层会不断积累热量，这样使得熔池内部温度与熔覆区域间的温度梯度逐渐缩小，随着熔覆层数的增加，熔体流速峰值下降幅度也逐渐减小。

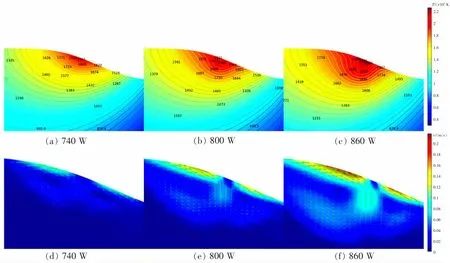
图6 不同功率下熔池温度场与速度场Fig.6 Temperature field and velocity field of molten pool under different powers

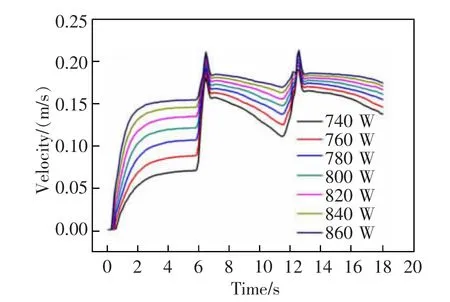
图7 激光功率对熔体流速峰值影响Fig.7 Effect of laser power on peak fluid velocity

2.2 光斑半径的影响

在熔覆过程中，光斑尺寸越大，激光束内能量密度越低。 图8 为不同光斑半径下的温度场与速度场分布图，由图8 可知：光斑半径的缩小不仅使得熔池温度及速度峰值均增大，同时熔池内整体流速和温度区域也增大。 图9 为不同光斑半径下熔池内流速峰值。 由图9 可知：随着光斑半径的缩小，不同阶段的熔池流速峰值均获得提升，同时使得熔体流速峰值在两次下降期的降幅逐渐减小，当光斑半径缩小至1 mm 时降幅趋向于平稳。 这是由于熔体流速主要由温度梯度所决定， 随着光斑半径的缩小，能量总输入不变，但光斑内能量密度会增加，温度梯度也随之增大，从而导致上升期的熔体流速峰值就越高。 并且由于光斑面积减小，激光加热区域与外界的换热区域减小，当能量输入与流失形成平衡时，从而使得熔池的熔体流速峰值趋于平稳状态。

图8 不同光斑半径下熔池温度场与速度场Fig.8 Temperature field and velocity field of molten pool under different spot radius

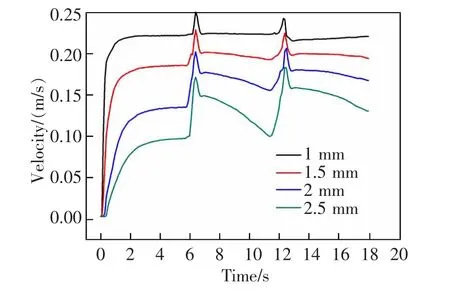
图9 不同光斑半径下熔池流速峰值Fig.9 Peak fluid velocity of molten pool under different laser spot radius

2.3 扫描速度的影响

除了激光功率以及光斑大小外，不同的扫描速度也会对熔池的温度场和速度场造成影响，扫描速度越慢意味着相同移动距离内输入熔池能量就越多。 图10 为不同扫描速度下熔池内温度场与速度场，由图10 可知，随着扫描速度的降低,熔体的温度和流速峰值及高温和高流速区域的尺寸会逐渐增大。 图11 为不同扫描速度下熔池内部速度峰值随时间变化曲线， 由图11 可知， 随着扫描速度的降低，当进行第一层熔覆时，熔池内部熔体流速峰值有明显的提升，当激光返回初始点时，熔体流速的下降幅度逐渐减小。 这主要是因为随着扫描速度逐渐降低,熔池所获得输入能量升高，导致熔池内温度梯度增大， 而熔池流速与温度梯度呈正比关系，从而导致熔池流速峰值在初始期有明显提升。 同时累积在熔池的热量随着扫描速度降低迅速增加，但系统与外界的换热效率有限，这使得随着扫描速度降低，熔池内热量逐渐累积。 当热量输入与损失趋向于平衡时，流体流速下降会逐渐缓和。

图10 不同扫描速度下熔池温度场与速度场Fig.10 Temperature field and velocity field of molten pool underdifferent scanning speeds

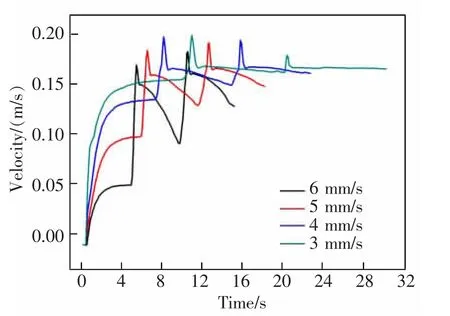
图11 不同扫描速度下熔池流速峰值Fig.11 Peak fluid velocity of molten pool under different scanning speeds

2.4 送粉率的影响

除了研究激光功率、光斑尺寸、扫描速度外，本文还研究了熔覆过程中送粉率对熔池温度场与速度场的影响。 由图12 和图13 可知，送粉率的增大只会增大涂层的高度，对熔覆过程中的温度场和速度场的分布以及各个阶段熔池内速度峰值基本没有影响。 这是由于送粉率的不同改变了单位时间内基板上粉末的堆积量， 但激光输入的能量并没有改变。送粉率对熔覆层的形貌尺寸影响非常大， 但对其过程中的温度场与速度场影响比较小。

图12 不同送粉率下熔池温度场与速度场Fig.12 Temperature field and velocity field of molten pool under different powder feeding rate

图13 不同送粉率下熔池流速峰值Fig.13 Peak fluid velocity of molten pool under different powder feeding rates

2.5 表面张力系数的影响

在激光熔覆的过程中，除了激光工艺参数能对熔池的温度场和速度场产生影响外，材料的表面张力系数也会对熔池的温度场和速度场造成影响。 在激光熔覆过程中，熔覆材料中活性元素的添加（如S元素等）会使其表面张力系数发生转变[22]，而材料表面张力系数会对熔池的流速和流动方向造成影响。如图14（a）所示，当材料表面张力系数取值小于0时， 熔池内熔体由激光中心区域向熔池边缘流动；材料表面张力系数取值大于0 时，熔池内熔体由熔池边缘向激光中心区域流动，但是两者流体流速峰值均出现在熔池表面边缘位置。 而熔池内流体的流动意味着热量的流动，如图14（b）所示，表面张力温度系数为负时，熔池内的热量消耗在熔池宽度上的扩展，使得熔池变浅变宽；表面温度张力系数为正时，熔池内流体流动驱使能量消耗在熔池深度的扩展，使熔池变深变窄[23-24]。

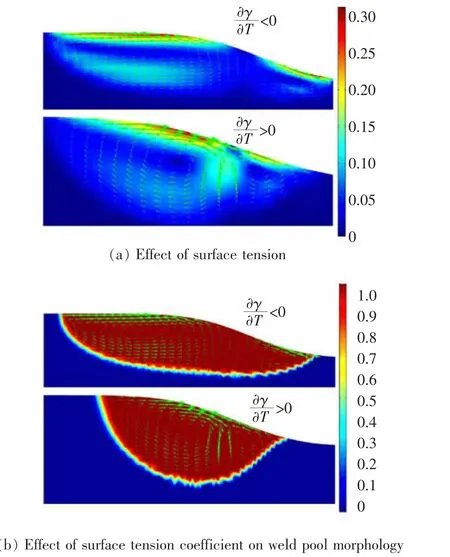
图14 表面张力系数对熔池的影响Fig.14 The effect of the surface tension coefficient on the molten pool coefficient on fluid flow direction

图15 为相同工艺参数的不同表面张力系数下熔池内部的熔体流速峰值。 由图15 可知，相同的表面张力系数下进行多层熔覆时，熔池内熔体流速相比前一层均会有一定程度的提升，同时熔池峰值增加的幅度变小，这是由于刚加工完的熔覆层会保留了一部分热源能量，当进行多层熔覆时，熔覆层积累的热量越多导致熔池温度峰值越高。 此外，由于熔池温度与基体温度的差值缩小，从而熔池温度峰值的下降幅度越小。

图15 不同表面张力系数下熔池流速峰值Fig.15 Peak fluid velocity of molten pool under different surface tension coefficients

表面张力系数取值正负不同情况下，两者形成的熔池形貌明显不同，系数为负值的熔池尺寸宽且浅，系数为正值的熔池尺寸深且窄，这是由于系数取值小于0 时， 熔体由熔池中心区域向周边流动，熔池与外界的接触增大， 加速熔池能量的散失，从而降低熔覆层稀释率； 而当系数取值大于0 时，熔体由熔池边缘向熔池中心区域流动，熔池与外界接触面缩小，阻碍熔池能量的散失，从而增大熔覆层稀释率。 综上所述，为制备优异质量的熔覆涂层，应选择表面张力系数为正值且取值较小的材料作为熔覆材料。

3 结论

本文通过COMSOL 多物理场软件建立热-流耦合模型，研究了激光熔覆过程中不同工艺参数和材料表面张力系数下熔池内部温度场和速度场的分布状况，并结合实验验证了COMSOL 软件中移动网格法模拟的熔覆层形貌的准确性，得出以下结论。

1） 采用移动网格法模拟出激光熔覆中熔覆层形貌，熔覆层的高度受送粉量的影响较大，熔池尺寸与激光功率呈正比关系，且模拟结果与实验结果吻合良好。

2） 进行多层激光熔覆时，增大激光功率、缩小光斑半径和加快扫描速度，均会使得熔池内部热量增多，从而提升熔池内熔体流速峰值，同时流速峰值下降幅度也会逐渐缩小。

3） 在激光熔覆过程中，熔覆材料的表面张力系数取值与熔体的流动方向具有重要关联性。 当表面张力系数取值小于0 时，熔池内熔体由熔池中心区域向熔池边缘流动，熔池与外界的接触增大，加速熔池能量的散失，从而降低熔覆层稀释率，使得熔池尺寸变浅变宽。当表面张力系数取值大于0 时，熔池内部熔体由熔池边缘向熔池中心区域流动，熔池与外界接触面缩小，阻碍熔池能量的散失，从而增大熔覆层稀释率，使得熔池尺寸变深变窄。