基于速度障碍法的三维确定型冲突探测模型

杨文达，吴明功，温祥西*，毕可心，蒋旭瑞

（1.空军工程大学空管领航学院,陕西 西安 710051；2.国家空管防相撞技术重点实验室,陕西 西安 710051；3.中国人民解放军94116 部队,新疆维吾尔自治区 和田 848000）

自由飞行的概念是由美国联邦航空局（Federal Aviation Administration，FAA）提出的。该概念的提出将保障飞行安全的责任由管制员转移给飞行员[1]。此飞行模式的提出，大幅提高了空域利用率，但增加了不同高度层间的航空器产生飞行冲突的概率，给空中交通安全带来巨大压力。冲突探测是保障飞行安全的基础与前提，常用冲突探测方法可分为概率型冲突探测方法和确定型冲突探测方法（几何法）。确定型冲突探测方法是根据航空器当前航迹（包括位置、速度等），不考虑其他因素的影响，预测航空器未来航迹并判断是否有冲突发生[2]。本文采用确定型冲突探测方法。

飞行保护区模型是研究冲突探测技术的关键。常用的飞行保护区模型包括：Reich 碰撞风险模型、圆柱状保护区、球状保护区和椭球状保护区。1966 年，Reich[3]首次提出航空器碰撞风险模型，把航空器简化成固定尺寸的长方体，计算碰撞危险和间隔之间的关系，解决了飞行间隔安全性评估问题。国际民航组织（International Civil Aviation Organization，ICAO）基于此模型建立了飞机的最小安全间隔标准[4-5]。圆柱状保护区、球状保护区和椭球状保护区即是基于Reich 碰撞模型提出的。圆柱状飞行保护区[6]的应用最为广泛，但由于圆柱体平面衔接处不可导的特点，在数值计算上具有局限性，因此，该模型多应用于航路航线上飞行冲突的探测。与圆柱状保护区相比，球状保护区处处可导，但增大了航空器间的垂直安全间隔，造成了空域资源的浪费，此模型多用于无人机的避障探测[7]。椭球状保护区由Menon 等[8]提出，在满足安全飞行要求的同时避免空域资源的浪费，具有很好的研究意义。2017 年，李冰冰[9]基于椭球状保护区，在平行航路、交叉航路场景下建立航空器冲突概率、冲突风险模型，将计算得到的扇区总体冲突频次等作为评估指标，对扇区整体进行安全评估。2019 年，蒋旭瑞等[10]以椭球状保护区建模，考虑不确定干扰因素，在集成学习分类器中进行中短期飞行冲突探测，提高了冲突探测准确率，降低了虚警率。相较于其他3 种保护区模型，椭球状保护区在不产生数字中断情况下，加强了航空器的间隔限制，在自由飞行条件下有更好的研究意义，近年来被学者们广泛关注，但是椭球状保护区给传统冲突探测方法的应用增加了计算难度，因此在确定型冲突探测方法中应用较少。

速度障碍法由Fiorini 等[11]提出，该方法易于理解且操作简单，在机器人自主避障研究[12-13]中得到了很好的应用。Durand 等[14]在飞机冲突探测方面引入速度障碍法，在航空器进入保护区之前仅依据航空器的当前位置和运动状态即可探测在未来一段时间内飞机是否存在潜在飞行冲突。王泽坤等[15]在圆柱型保护区基础上引用速度障碍法，以期解决同高度层航路航线上的飞机冲突问题。但在自由飞行条件下，飞行冲突不再局限于同一高度层，因此，本文基于速度障碍法，建立三维空间内的飞行冲突探测模型，以期应用于实际，减少管制员工作负荷，保障飞行安全。

1 建立飞行保护区

在自由飞行条件下，每架航空器周围的空域可划分为3 个层次，包围航空器最里层区域被称为保护区，当2 架或2 架以上航空器的保护区发生重叠时，即可视为存在飞行冲突。在本文中，假设飞机在飞行过程中，始终做匀速直线运动。

在自由飞行、雷达管制条件下，飞机航迹要受到雷达探测精度、气压、风等多种不确定性因素的影响，采用传统安全间隔标准建立的飞行保护区不足以模拟飞机的真实飞行状态，若在此条件下进行飞行冲突探测会存在误差。如图1 所示，本文采用椭球状保护区作为安全保护区模型，将椭球中心目标机视为坐标原点，建立空间直角坐标系O-xyz，其中x，y，z轴方向依次为飞机航向的反方向、航向的左侧方向和机身的垂直方向。为了符合ATC 标准[16]，取椭球体的长焦距为dv=5 nmile(1mile=1.609 344 km)，短焦距为dl=2 000 ft(1ft=0.304 8 m)。

图1 椭球状飞行保护区

因此，航空器的冲突域S可以表示为

式中：(x,y,z)为椭球中心目标机的坐标；(x0,y0,z0)为潜在冲突机目标。

2 模型建立

此模型的基本思想是根据航空器当前航迹（包括位置、速度等），不考虑其他因素的影响，判断航空器在相遇几何空间内是否存在潜在飞行冲突，并依据存在冲突飞行场景中的冲突机与相对冲突点距离求出预计冲突时间。

速度障碍法定义了一个相对速度障碍区域，当相对速度落入该区域时，则视为2 机之间在约束的时间内会发生飞行冲突[14]。它简化了飞机冲突的探测条件。在传统速度障碍法中，目标机与冲突机在同一高度层，冲突的探测模型被定义在二维平面内，然而在现实情况中，飞机飞行高度层未知，速度方向未知，在不同高度层中，仍存在发生飞行冲突的危险。因此，本文基于改进的三维速度障碍模型实现对飞行冲突的探测和解脱。在应用速度障碍法进行冲突解脱时，应改变相对速度矢量，直到其完全脱离速度障碍区域时，则2 机视为不再存在潜在冲突。

2.1 二维速度障碍模型

在二维速度障碍模型中，航空器的保护区为圆柱状飞行保护区，如图2 所示，底面半径为dv，圆柱高为2dl，飞机AC1和飞机AC2在同一高度层飞行，速度分别为v1和v2，AC1相对于AC2的速度为vr=v1-v2。图3 为二维平面内基于速度障碍法的冲突探测示意图，由于2 架飞机在同一高度层，因此AC2的圆柱形保护区在此高度层上的曲截面为以点B为圆心，dv为半径的圆B，则速度障碍区域RCC由顶点A及A与圆B切线所包围的区域。当相对速度vr与速度障碍区域RCC的交集非空时，则视为在同一高度层上的2 架飞机存在冲突。

图2 圆柱状飞行保护区

图3 二维速度障碍模型

2.2 基于速度障碍法的三维冲突探测模型

在二维速度障碍冲突探测模型中，航空器的保护区模型为圆柱状保护区，其上下表面衔接处不可导，这使得应用该模型在三维空间中进行冲突探测时，增大了数值计算上的局限性。因此，本文选取椭球状保护区，结合速度障碍法，研究自由飞行条件下的冲突探测方法。

基于二维速度障碍模型思路，建立三维速度障碍探测模型，如图4 所示，将椭球中心目标机、潜在冲突机分别用P1、P2表示，P1的速度为v1，P2的速度为v2。在速度障碍模型中，发生冲突与否只与飞机间的相对位置和当前状态有关。以P2作为参照点，则P1相对P2做相对运动，相对速度为vr=v1-v2。

图4 速度障碍法示意图

定义三维速度障碍锥RCC，即飞机会发生碰撞时的相对速度vr的集合。

式中：lr为相对速度vr延长线。

通过上述描述，做出判断如下：当相对速度vr与相对速度障碍区RCC交集非空时，即vr∩RCC ≠∅时，2 机存在飞行冲突，需要进行冲突解脱；当vr∩RCC=∅时，2 机不存在飞行冲突。

如图5 所示，显然vr∩RCC ≠∅时，lr与冲突域S有2 个交点。其具体求解步骤如下。在三维坐标系O-xyz中，不规定vr方向的情况下，将vr所在直线lr与椭球面方程联立，则lr与椭球的交点满足方程组，为：

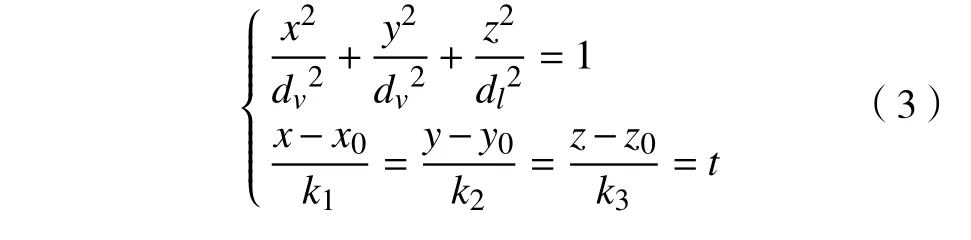
图5 三维速度障碍模型

式中k1，k2，k3为lr方向向量在x，y，z轴上的分量。求解得

记lr与冲突域S的交点个数n，根的判别式为Δ=b2-4ac，其中a，b，c分别为多项式方程(5)中t2，t，1 的系数。

Δ ＞0时，记交点坐标为L1，L2，则预计冲突时间T可表示为

可做出如下判断：当Δ ≤0时，vr∩RCC=∅，2 机不存在潜在飞行冲突；当Δ＞0时，n=2，vr∩RCC ≠∅，2 机存在潜在飞行冲突，预计冲突时间为T。

3 仿真验证

为了验证该冲突探测算法的可靠性，应用MATLAB对上述理论进行仿真分析。如表1 所示，在4 种场景下，每架飞机均已给定初始坐标、起始航向及速度大小。针对飞机的位置和速度信息，首先通过预测2 机航迹，对4 种场景下2 机之间的真实冲突关系进行判断，若2 架飞机在同一时刻水平间隔和垂直间隔均小于安全间隔距离，则视为2 机存在潜在飞行冲突。然后，求出每一场景下的 Δ值，并与2.2 节中的三维冲突探测模型的冲突成立条件进行对比分析。若仿真所得到的结果与各场景下的飞机间的真实冲突关系相吻合，则可判定此冲突探测方法是可靠的，并对存在潜在飞行冲突的场景计算预计冲突时间。

表1 位置信息

首先，根据2 机间隔与安全间隔的关系判断4 个场景下，飞机间是否存在飞行冲突。基于2 机的初始速度和航向，在2 机运动状态不发生改变的情况下，预测2 机航迹。图6 示出在4 种场景下，2 架飞机P1、P2间的水平间隔、垂直间隔随飞机P1位置的变化关系。图中蓝线表示2 机某时刻的水平间隔与垂直间隔，红线为水平安全间隔和垂直安全间隔。根据飞行冲突的定义，若某一时刻，2 机间的水平间隔和垂直间隔在同一时刻均低于安全间隔距离时，则视为2 机存在潜在飞行冲突，否则不存在飞行冲突。在图中，飞机在场景1、3 中，2 架飞机均存在潜在飞行冲突，在场景2、4 中，2 机不存在潜在飞行冲突。结合表2 分析：存在飞行冲突的场景1、3 中，Δ ＞0，与2.2 节中三维冲突探测算法的飞行冲突成立条件相吻合，故可预计冲突时间分别为0.234 h，15.4574 h；不存在飞行冲突的场景2 和4 中，Δ ＜0，满足2.2 节中的无冲突条件。在场景2 中，结合图表，可以看出，虽然2 机未发生冲突，但在飞行过程中，2 机恢复安全垂直间隔距离后的短暂时间内，其水平安全间隔距离丢失，在此接近临界冲突场景下，Δ＜0，算法是有效的。故通过仿真验证得到，在不考虑其他干扰因素的情况下，基于速度障碍法的三维冲突探测模型是可靠的。

图6 不同场景下2 机间隔随x 坐标变化图

表2 不同场景下的 Δ值及预计冲突时间T

4 结论

本文在假设航空器始终保持匀速直线飞行的条件下建立飞行冲突探测模型，并经过仿真验证，证实该模型在一定规则下可有效探测三维空间内的飞行冲突，并计算预计冲突时间。该模型简单、计算方便，但该模型假设飞机做匀速直线运动，没有考虑其他条件（误差因素、飞行员意图、反应时间等）；因此，此模型主要适用于航空器在航线飞行阶段的飞行冲突探测。对于航空器做直线非匀速飞行的场景，本文的研究思路，同样可以进行预测，但对于未来飞行轨迹难以预测的场景，还需要做更深入的研究。