自由航路空域的出入口位置布局优化
2021-11-20魏路欢陈创希魏志强
魏路欢,陈创希,周 兴,魏志强*
(1.民航航空公司人工智能重点实验室,广东 广州 510000;2.中国民航大学空中交通管理学院,天津 300300)
自由航路空域(free route airspace,FRA)是欧洲单一天空项目(single european sky ATM research,SESAR)的重要组成部分,是空域一体化改革与扩容增效的重要举措,可以降低航空器的飞行时间、燃料消耗、飞行成本以及对环境的影响。目前欧洲3/4 的空域都已实现自由航路空域[1]。在自由航路空域飞行时,只需选定入口和出口,航空器就可以按照大圆航线穿过这个空域[2]。
Reynolds[3]针对不同飞行阶段和地理区域,找出了衡量实际飞机轨迹与理论上最短飞机轨迹之间偏差的效率指标;Siddiquuee[4]给出了用于航路网络优化的一系列数学模型,包括航路网络节点的潜在冲突系数、航路容量、航路距离等;Steve[5]提出飞行计划优化策略,以实现最佳航线、高度、速度和加油量的优化。上述研究都是基于传统的航路网空域开展的,没有考虑自由航路空域(FRA)的特殊性以及对航路优化的影响。
严伟等[6]针对航路网络的运行成本和安全性相冲突问题,考虑多种不确定因素的影响,建立了不确定条件下的航路点布局优化模型;严伟等[7]从航路网络经济性和安全性出发,对航路点布局进行了优化;余朝军等[8]在多种约束的基础上,建立了航班—登机口分配的多目标非线性0-1 整数规划模型,提高了登机口的利用效率和乘客的换乘舒适度;郭野晨飞等[9]采用基于航班优先级排列的染色体编码方式,设计了一种改进的遗传算法,提高了空域运行效率;王世锦等[10]阐述了3 大类航路网络规划研究技术的实施原理、存在的优缺点及不同环境下的适用性,为交通规划理论提供了更多的借鉴;李文等[11]提出基于可靠度的备件保障中心多目标选址模型,可作出运输路径最短、总成本最小的最优选址决策;王瑛等[12]以成本和冲突系数作为航路点布局点问题的目标函数,构建了航路点布局优化问题模型。上述研究主要针对交叉航路对航路点位置布局进行优化,没有考虑自由航路空域(FRA)中的出入口优化问题。
针对自由航路空域划设中的出入口位置布局优化问题,本文建立了空域限制条件模型,并以航班加权距离偏差为目标,构建了给定出入口数量下的位置优化模型,采用基于精英保留的遗传算法进行了求解,最后选取欧洲某典型空域进行优化分析。结果表明,在给定出入口数量的前提下,通过对自由航路空域出入口进行位置的布局优化,可缩短航班航程,提高飞行效益。
1 自由空域出入口布局优化模型
自由航路空域边界的出入口位置布局优化模型的构建,主要包括建立空域限制条件模型和优化目标计算模型。
1.1 空域限制条件模型
在一个自由航路空域中,虽然空域的范围很大,但对于决策变量即分布在边界的出入口的位置坐标来说,变动范围应该是有限的,即有空域边界点位置约束。空域边界点位置约束是指所有待优化的边界出入口的位置变动范围不能是全局航路网络,应约束在所在空域的进出边界上。

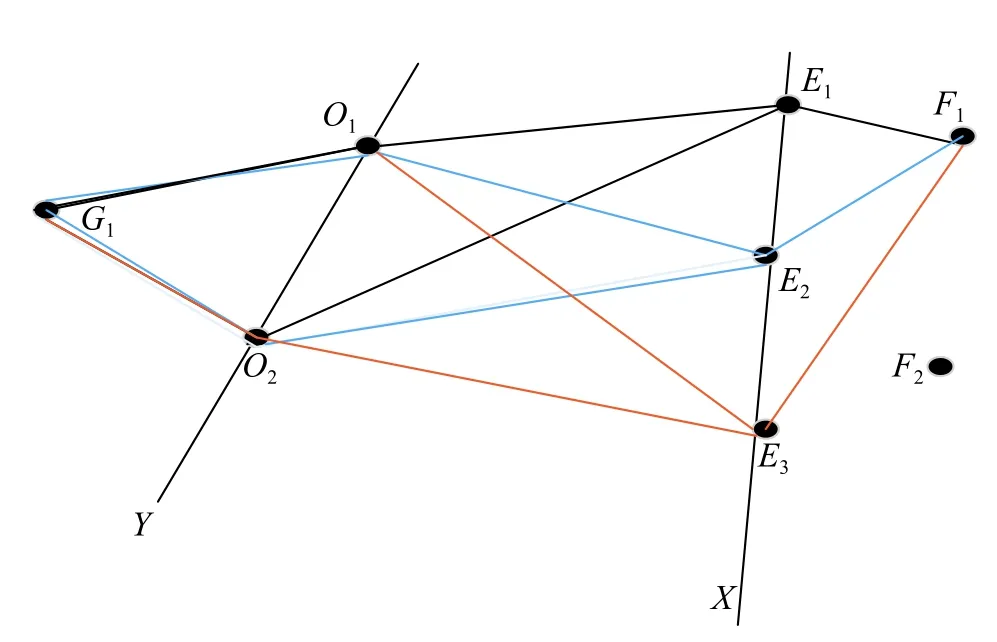
图1 自由航路区航线示意图
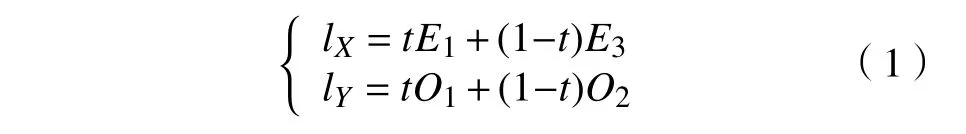
式中:t为0 与1 之间的随机数;E1为入口E1的经纬度对;E3为入口E3的经纬度对;O1为出口O1的经纬度对;O2为出口O2的经纬度对。
1.2 优化目标计算模型
已知空域外n个起点{F1,F2,···,Fn}、进入边界x个入口{E1,E2,···,Ex}、离开边界 y个出口{O1,O2,···,Oy}以及空域外m个终点{G1,G2,···,Gm}的经纬度坐标。在自由航路空域外有n个起点m个终点的情况下共有(n×x×y×m)种飞行路径组合,在路线组合中选择起点和终点一一对应的最优飞行航线的模型为:
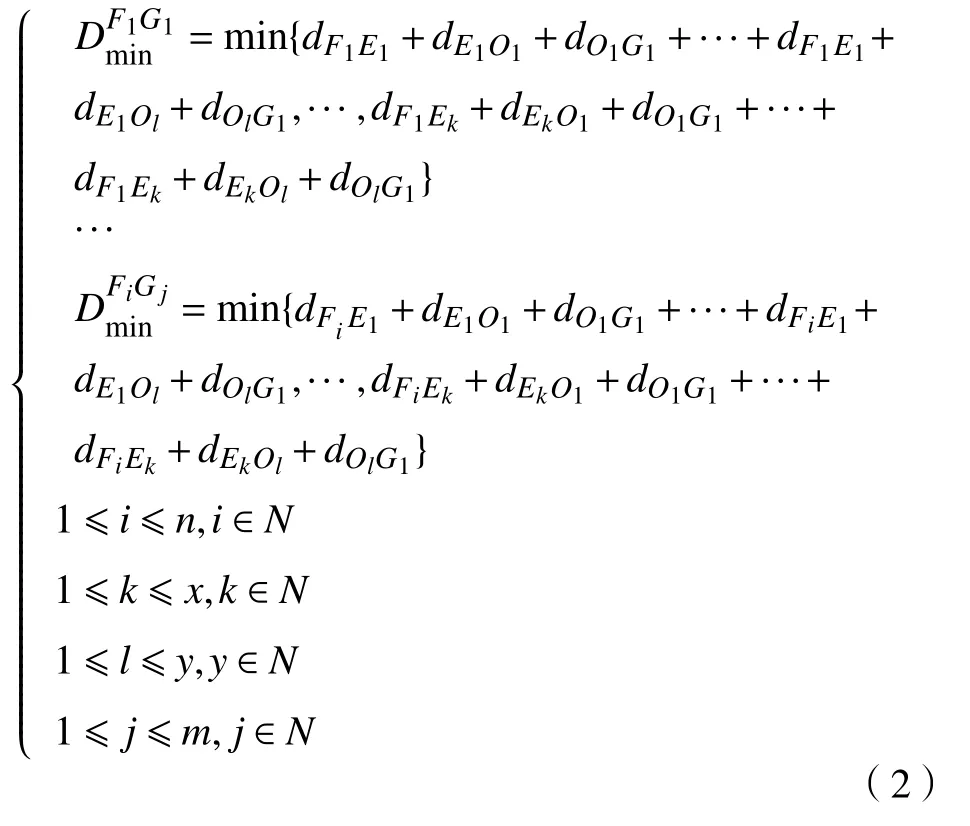
式中:dFiEk为空域外起点Fi到进入边界入口Ek的直线距离;dEkOl为进入边界入口Ek到离开边界出口Ol的距离;dOlGj为离开边界出口Ol到空域外终点Gj的距离;为空域外起点Fi到空域外终点Gj路线组合中的最短总距离。
算法模型的适应度为自由航路空域外有n个起点m个终点的飞行路线组合的航班加权距离偏差g,即实际航班加权距离与航班加权大圆航线距离的偏差值。航班加权距离偏差能够直观地表达出优化后的实际航班加权距离与大圆航线距离的接近程度,偏差越小,则实际飞行越接近直线飞行,航程越短。
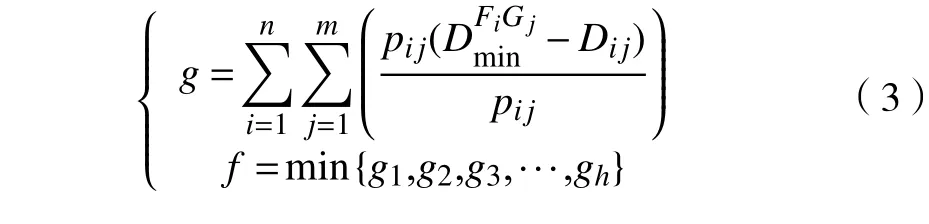
式中:pij为实际情况下从空域外Fi起点到空域外Gj终点的航班飞行量(/月份);Dij为空域外Fi起点到空域外Gj终点的大圆航线距离;gh为在一定出入口数量的情况下,出入口坐标位置不同的第h个方案。
1.3 出入口优化流程设计
不同数量的边界出入口,得到的穿越自由航路空域的飞行路线也有很多种,每条航线的距离不同,计算量巨大。本文采用精英保留的遗传算法,在基础遗传算法的基础上加快了收敛速度,得出较为合适的进出口数量以及对应的最优分布位置。具体流程如图2 所示。
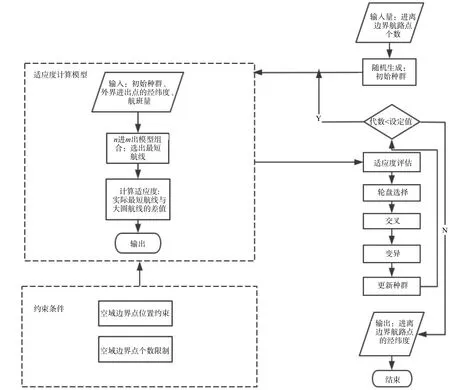
图2 基于遗传算法的自由航路空域边界出入口优化流程
1)输入自由航路空域边界入口的数量x和离开边界出口的数量y,随机生成初始串结构,初始串长度为空域边界出入口的数量和。采用实数编码,根据输入的空域出入口的数量,随机生成x个入口的纬度坐标集和y个出口的纬度坐标集,其中,Etx为第x个入口的纬度,Oty为第y个出口的纬度。。当有M个个体N,则构成了算法的初始种群M。
2)调用计算适应度的函数模型,通过式(3)计算出适应度值。适应度值越小,代表该个体的性能越好,越满足适应条件。
3)采用轮盘赌的方式选择适应度较高的父代种群,进行交叉、变异等遗传操作并更新种群,交叉概率为0.9,变异概率为0.1。
4)找出父代种群中最优的个体,将其保存,使其基因染色体不会被遗传操作破坏掉,然后替换掉经过交叉、变异之后子代种群中,适应度最差的个体。
5)进行循环操作,直到迭代次数等于设定次数。得到的最优个体即为算例所求的航班加权距离偏差,对应的自变量为不同数量下的自由航路空域边界出入口对应的最优经纬度坐标。
2 典型空域的出入口布局优化分析
2.1 实验数据
该算例分析的是地理位置临近葡萄牙的一块自由航路空域。该空域的边界由航路点连接而成,呈不规则八边形,如图3 所示。空域外起点为{B5、B6、B7、B8、B9},空域外终点为{A6、A7、A8},空域入口为{AMSEL、A1111、A2222、A3333、A4444、A5555、BATAX},空域出口为{LUTAK、KOMUT、GUNTI、ERPES、DETOX、BANAL}。
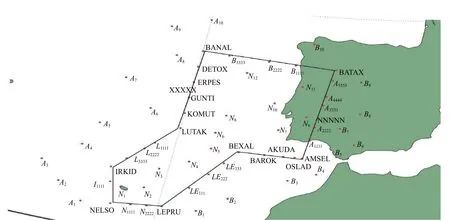
图3 欧洲某自由航路空域图
主要分析空域外起点{B5、B6、B7、B8、B9}穿越进入边界NNNNN和离开边界XXXXX,到达空域外终点{A6、A7、A8},从2020 年6 月1 日到6 月30 日的航班飞行情况。具体航班数量和从空域外起点到终点的15 种大圆航线距离以及实际飞行距离如表1 所示。实际飞行距离为空域外起点经过当前出入口到达空域外终点的航线距离。
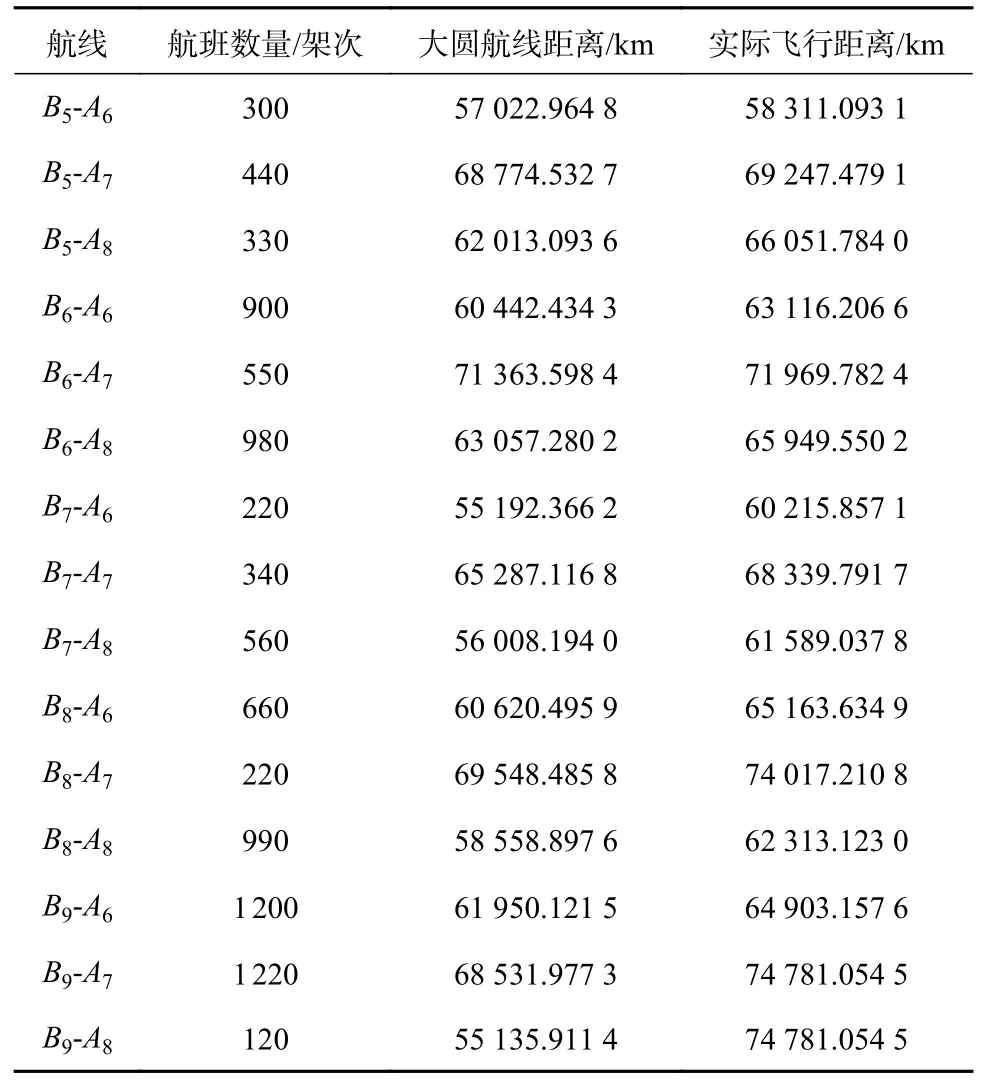
表1 不同航线上的航班量以及对应的直飞距离
针对上述数据,计算出在当前的出入口位置布局下,航班加权距离偏差为3 661 km,即为航班加权大圆航线距离的5.832 3%。在优化自由航路空域出入口位置的过程中,首先设定自由空域出入口的数量分别为x=4和y=4,算法随机生成该数量的出入口经纬度坐标,然后分别计算5×x×y×3=240 条航线的航线距离,根据空域外n个起点m个终点中选最优模型,选出最短航线,计算出航班加权距离偏差,即为该方案下的适应度。然后经过精英保留的遗传算法进行初始种群—边界入口和出口经纬度坐标的交叉、变异等操作,得出新的种群。该种群保留了父代种群优良基因,再进行循环计算,直至得出在给定出入口数量下的最优分布位置坐标。
2.2 位置优化结果分析
根据上述航班信息,保持现有空域边界的出入口分别为4 的数量不变,交叉概率为0.9,变异概率为0.1,对边界出入口的位置布局进行优化。图4为传统遗传算法进化图,航班加权距离偏差代表的算法曲线在600 代以内逐渐下降,在800~1 200 代收敛,得出最优结果。图5 为精英保留的遗传算法进化图,航班加权距离偏差代表的算法曲线在50 代以内快速下降,之后下降速度减慢,在150~500 代之后逐渐趋于平稳,其航班加权偏差为263.473 4 km,为航班加权大圆航线距离的0.419 7%,比优化前降低了5.412 6%。
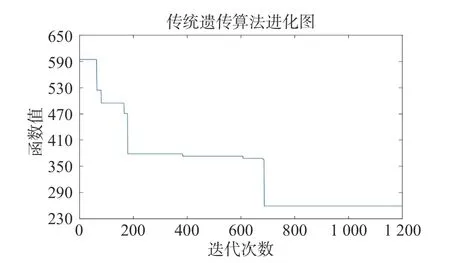
图4 对出入口位置分布优化的传统遗传算法迭代图
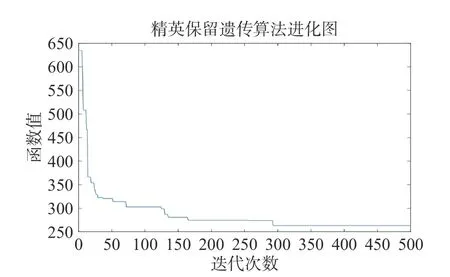
图5 对出入口位置分布优化的基于精英保留的遗传算法迭代图
通过对比2 种算法的迭代图,可以看出基于精英保留的遗传算法在传统遗传算法的基础上加快了收敛速度,减少了迭代次数,提高了优化速率。
进入边界NNNNN 上优化后的入口和离开边界XXXXX 上优化后的出口位置分布分别为{x1、x2、x3、x4},{y1、y2、y3、y4},在图6 中用黑色圆点表示。图6 为空域外起点B9经过优化后的出入口到达终点A6、A7、A8的航线与对应的未优化前的实际飞行航线的直观对比。其中,黑色线段代表未优化前的飞行航线,红色线段代表起点B9到终点A6的优化航线,蓝色线段代表起点B9到终点A7的优化航线,黄色线段代表起点B9到终点A8的优化航线。从图中较直观地看出,优化后的航线较优化前的航线更接近大圆航线,飞行距离明显缩短。几个空域外起点到达空域外终点的优化航线在图中显示忽略。
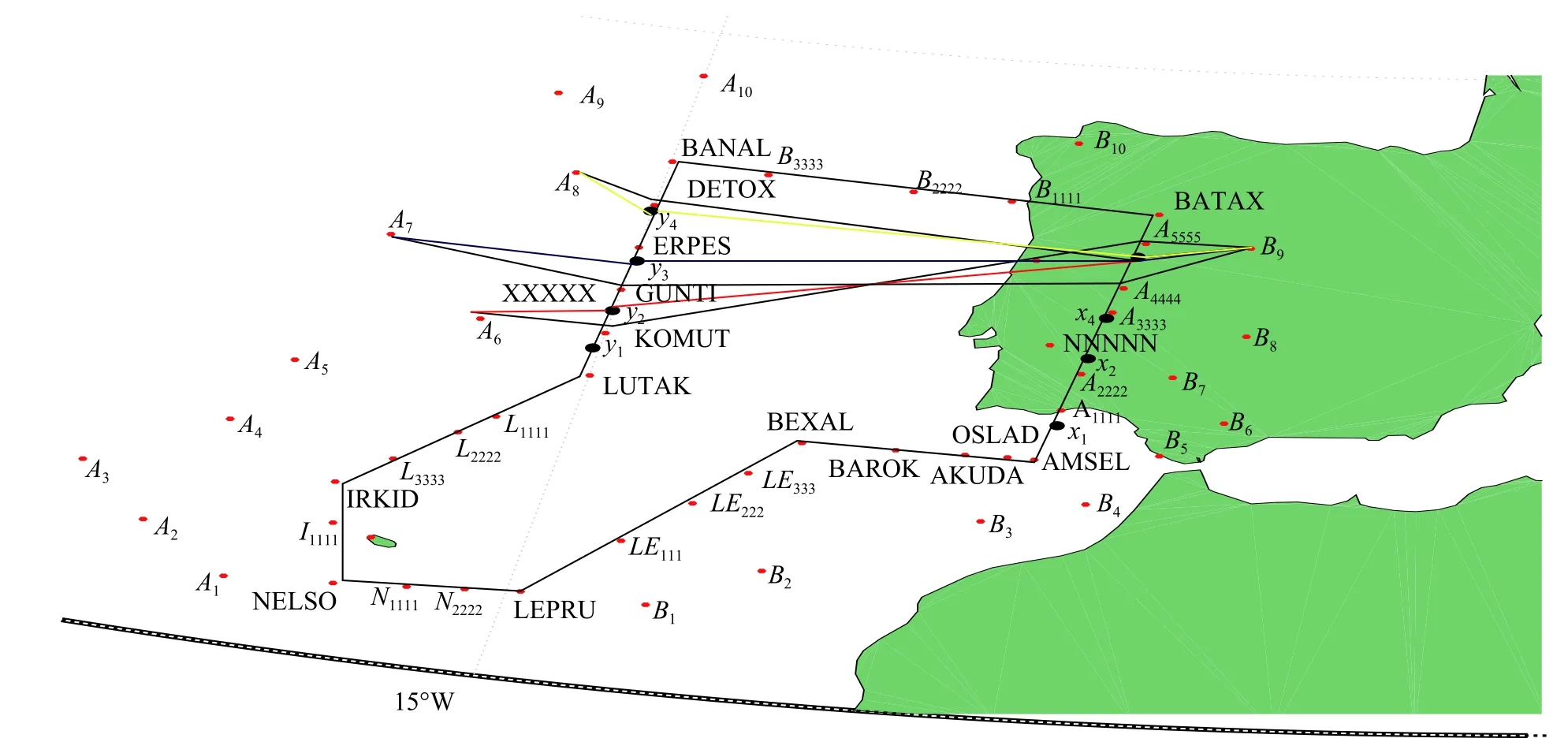
图6 优化后的航线与优化前的航线对比图
2.3 出入口数量的影响分析
通过设定不同数量的自由航路空域出入口,可以得出不同的航班加权距离偏差。出入口数量越多则航班加权距离偏差就越小,结果越优异,但一味增加出入口数量是不现实的。图7 为不同数量的出入口对应的航班加权距离偏差和其占航班加权大圆航线距离的比重。
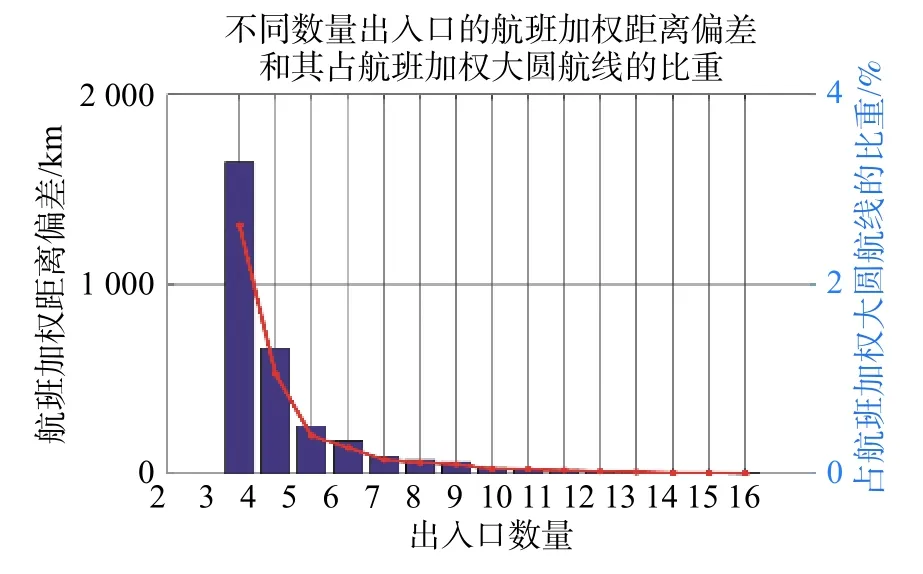
图7 不同数量出入口的航班加权距离偏差和其占航班加权大圆航线的比重
由图可知,当自由航路空域出入口数量为7 或者8 时,再通过增加出入口的个数来缩小航班加权距离偏差,其效果已不明显。即对于空域外有n个起点、m个终点的情况下,FRA 的出入口数量达到(n×m×50%)时,优化的效果即可接近于直线飞行。
3 结论
本文针对自由航路空域的划设与出入口优化问题,建立了以航班加权距离偏差为目标的优化模型,并以典型空域为例进行优化分析。
1)通过对现有空域出入口的位置进行优化,能够在原有实际航班加权距离偏差的基础上减少5.412 6%。这说明优化空域出入口的位置能够有效的缩短航程,提高飞行效益。
2)虽然增加空域出入口数量,会使优化效益提高,但是当超过空域外起点和终点数量乘积的50%时,优化的效果已接近于直线飞行。
