基于渣层增长模型的水冷壁背火侧温度表征特性
2021-11-17杨建国臧慧敏邓芙蓉谢晓强
杨建国, 臧慧敏, 邓芙蓉, 谢晓强, 赵 虹
(1.浙江大学 能源清洁利用国家重点实验室,杭州 310027;2.浙江天地环保科技股份有限公司,杭州 311121)
燃煤电站锅炉水冷壁结渣是锅炉运行过程中普遍存在的问题,严重影响了锅炉的经济性和安全性,有效监测锅炉结渣状况对锅炉安全运行具有指导意义。结渣的形成主要与燃煤的煤质和锅炉的运行方式相关。研究表明,我国机组使用的煤种约半数为易结渣类型。电站锅炉燃用煤种多变,实际燃用煤种的煤质经常偏离设计值,不同煤种的燃烧特性和结渣特性差异又给预防结渣带来较大难度。目前,国内外学者针对锅炉结渣问题进行了广泛研究[1],提出了多种结渣监测方法,包括采用红外照相设备等直接诊断法[2]、炉膛出口烟温法[3]、热流计法[4]、炉内热有效系数法[5]和背火侧鳍片温度表征法[6-8]等。其中背火侧鳍片温度表征法是基于背火侧鳍片特定点在结渣厚度变化下具有良好的温度特性曲线,将其作为结渣判断的特征参数来反映水冷壁结渣状况,具有显性的表征能力,且具有易安装维护、可大面积覆盖及可定点判断的优点。
采用背火侧鳍片温度表征法首先要了解水冷壁鳍片管的温度分布,选取有效特征温度,并掌握渣层及运行工况变化对特征温度的影响关系。水冷壁温度场的研究,一般是通过建立水冷壁的数学模型,把问题简化为定边界条件的多元导热微分方程组,然后采用解析解法[9]或数值方法[10-11](有限差分、有限元、有限体)进行求解。边界条件中的水冷壁向火侧壁面的实际热负荷可选用角系数法[12]或辐射换热法[13]确定,其中辐射换热法考虑水冷壁向火侧烟气温度对水冷壁辐射热流密度的影响。对于结渣水冷壁,渣层形状对其温度场存在不可忽略的影响,但已有研究中所建立的渣层模型均为固定的渣层形状[7-8],并未考虑渣层形状随结渣厚度而发生的变化。另外,水冷壁的鳍片与水冷壁管之间是否带有焊脚,对水冷壁温度场也存在明显的影响[10],目前的相关文献基本没有涉及。
笔者考虑到结渣厚度不同其表面形状也会不同,定义了新的渣层增长模型,同时根据水冷壁管与鳍片间的焊脚结构,建立更切合实际的水冷壁结渣物理模型,利用Fluent进行相应的换热数值模拟,从而研究结渣厚度和锅炉运行的关键因素对水冷壁背火侧特征温度的影响规律,为背火侧鳍片温度表征法实时监测水冷壁结渣及建模提供更精准的理论依据。
1 计算模型
1.1 研究对象
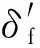

图1 带焊脚的膜式水冷壁结构

表1 水冷壁结构参数
水冷壁导热系数λ与其壁面温度tw有关[14]:
λ=62.992 7-0.030 7tw
(1)
1.2 渣层增长模型
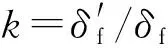
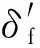
(2)


Ⅰ型
p1和p2的取值与水冷壁结构和k值有关。本文中,当渣层形状为Ⅰ型和Ⅱ型时,k为定值,取k=2.0[6]。根据几何结构计算,得到p1=8 mm,p2=27 mm。
1.3 水冷壁传热模型
结渣的水冷壁主要接受炉内高温火焰的辐射加热,然后通过结渣的管壁导热将热量以对流换热的方式传递给管内工质,实现冷却作用,过程如图3所示[13]。其中,Jhy为火焰对渣层表面的入射辐射热量,W/m2;R为渣层表面的反射辐射热量,W/m2;ts为渣层外表面温度,K;q为结渣水冷壁面实际换热量,W/m2;ε为外表面发射率;σ0为斯特藩-玻尔兹曼常数,取5.67×10-8W/(m2·K4);ti为水冷壁管内工质温度,K;αi为管内工质对流传热系数,W/(m2·K);E为渣层外表面温度下的黑体辐射量,W/m2。

图3 结渣水冷壁传热机理
由于渣层变化面向烟气,因此以烟气侧计算换热量,烟气侧换热可以认为是烟气与炉膛壁面间的相互辐射过程。考虑渣层表面接收的净辐射换热量与通过渣层的导热量的热平衡(取火焰发射率为1)[13],有:
(3)
其中,α为外表面吸收系数。根据基尔霍夫定律,不考虑表面温度对发射率的影响,则有:
α=ε
(4)
故而
(5)
由式(5)可知,结渣水冷壁实际换热量与外表面发射率ε、炉膛烟温Thy和渣层外表面温度ts有关。考虑到水冷壁与渣层的物性参数不同,两者表面发射率不同,清洁水冷壁的表面发射率为0.8[16],渣层的表面发射率为0.85[17]。
1.4 数学模型
水冷壁温度场的分布受向火侧的加热强度(由炉膛烟温Thy表示)、管内工质的冷却强度(由管内工质对流传热系数αi表示)及稳定工作状态下水冷壁管内工质温度ti3个因素影响。为简化计算,结合渣层增长模型和传热模型,进行如下假设:
(1) 对于超(超)临界锅炉,管内工质始终是单相流动,随着工质流动、吸热温度逐渐升高,但沿管子轴向温度梯度(约为2.5~6.5 K/m)与截面内径向温度梯度(约为5 000~15 000 K/m)相比很小,所以轴向导热可以忽略不计[18],故可以看成任一截面的二维问题。
(2) 由于锅炉在启停和变负荷运行时温度随时间的变化率很小(小于3 K/min),对于监测系统来说水冷壁温度场变化率足够缓慢,可将水冷壁管壁和鳍片中的传热过程看成各个时间点的稳态导热。
(3) 背火侧可认为绝热,即膜式水冷壁经炉墙的散热忽略不计。
(4) 向火侧壁面只考虑与炉膛内部的辐射换热,由于对流换热占比小于5%,故可忽略。
(5) 膜式水冷壁的金属材料是均匀且各向同性的,只考虑其导热系数随温度的变化。
(6) 水冷壁管内工质温度和对流传热系数沿周向均匀分布,并在给定工况下稳定不变。
(7) 渣层形状由渣层增长模型确定,结渣时渣层与壁面紧密连接,不考虑渣层与壁面之间的接触热阻,渣层的导热系数不随温度变化而变化。
基于以上假设,将问题简化为二维、稳态、无内热源的导热问题,根据假设(5)和假设(6),水冷壁截面温度场应该左右对称,故计算区域只选取水冷壁截面的一半(区域ABCDEFGH,见图1),其中向火侧壁面为DEF面,背火侧壁面为ABC面,管内壁面为GH面,对称面为AH面、FG面和CD面。整个计算区域的导热微分方程和边界条件如下:
(6)
式中:t为结渣水冷壁的温度分布,K;λf为渣层的导热系数,取值为1.5 W/(m·K);x,y分别为水冷壁与鳍片的平行方向和垂直方向;n为界面的法向。
(7)
式(6)是典型的二维导热微分方程,采用有限元法进行结渣水冷壁温度场的求解。
1.5 工况选取
根据渣层增长模型,选取以下鳍片结渣厚度进行模拟:清洁管壁为0 mm;Ⅰ型取2 mm和6 mm;Ⅱ型取8 mm、12 mm、16 mm、20 mm和24 mm;Ⅲ型取28 mm、35 mm、45 mm和65 mm。利用GAMBIT对模型进行网格划分,采用均匀化四边形网格,如清洁水冷壁和结渣厚度为35 mm的水冷壁网格数分别为41 472和532 305。
所研究的锅炉在不同工况下的水冷壁工质温度如表2所示,BMCR工况为锅炉最大连续蒸发量工况。据研究,在亚临界压力下,管内工质处于单相区时,对流传热系数随工质焓值增加而增大;在超临界压力下,当工质温度处于拟临界温度时,管内工质对流传热系数处于峰值状态[19]。工质在水冷壁内的温度介于进口温度和饱和温度(拟临界温度)之间连续变化,其对应的对流传热系数自然也处于两者之间且连续变化。因此,根据实际运行参数(见表2)和文献[11]中的计算方法,计算得到不同工况下水冷壁管内工质进口温度和饱和温度对应的对流传热系数,即不同工况下对流传热系数的最小值和最大值,如图4所示。图4中阴影部分为水冷壁管内工质的对流传热系数变化区间。

表2 不同工况下的水冷壁工质参数
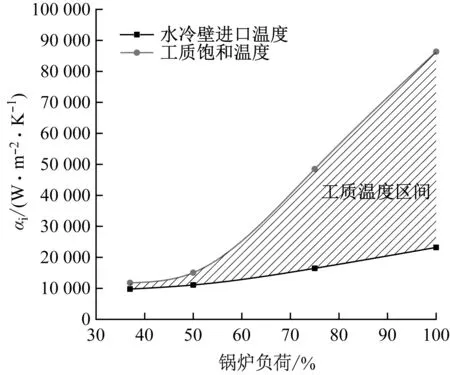
图4 不同工况下管内工质对流传热系数变化区间
根据上述结果以及锅炉实际运行状况,选取工况如下:工质温度ti选取520 K、570 K、600 K、650 K和700 K,炉膛烟温Thy取1 300 K、1 400 K、1 500 K、1 600 K、1 700 K和1 800 K,管内工质对流传热系数αi取3 000 W/(m2·K)、5 000 W/(m2·K)、10 000 W/(m2·K)、15 000 W/(m2·K)、20 000 W/(m2·K)、25 000 W/(m2·K)、50 000 W/(m2·K)和100 000 W/(m2·K)共计240个工况组合,对不同结渣情况下的水冷壁温度场进行数值模拟和分析。
1.6 模型验证
文献[20]中采用电模拟试验方法得到了水冷壁截面温度场。采用本文计算模型计算了相同锅炉运行工况下的清洁水冷壁温度场,得到水冷壁鳍片中点D点与外壁面中点F点的温差ΔtDF随工质对流传热系数的变化关系,结果见图5。由于两者水冷壁结构和物理参数以及水冷壁实际接受热负荷的计算方法不同,ΔtDF计算结果与试验结果的绝对数值有所差异,但两者变化规律基本一致,说明本文所用计算模型及计算过程是可行的。
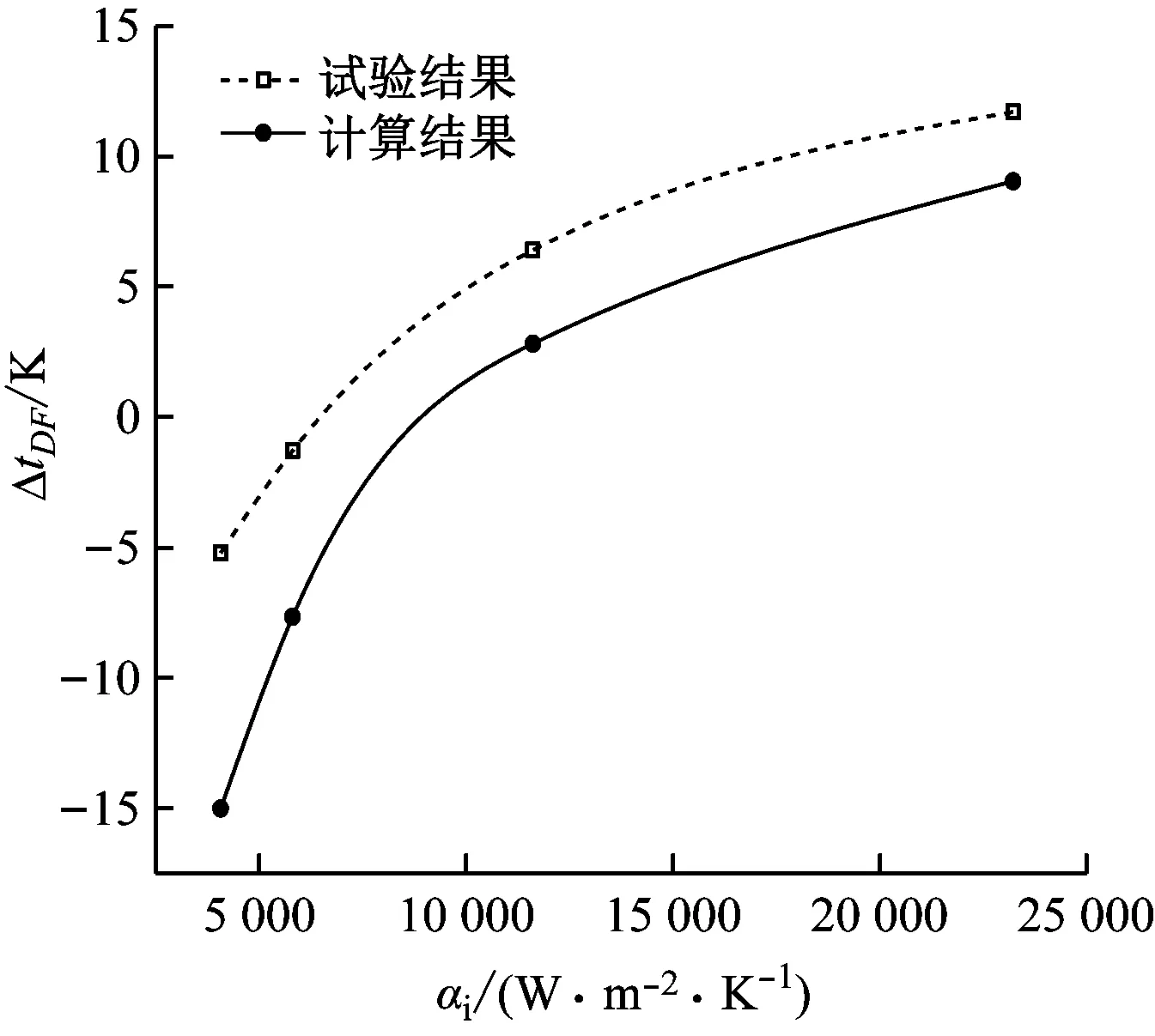
图5 温差ΔtDF与工质对流传热系数αi的关系Fig.5 Relationship between ΔtDF and αi
2 模拟结果与分析
2.1 结渣对水冷壁温度场分布的影响
图6给出了Thy=1 500 K,αi=25 000 W/(m2·K),ti=600 K,不同结渣形状的鳍片结渣厚度时水冷壁截面的温度场分布。水冷壁表面清洁时,最高温度tmax位于向火侧水冷壁鳍片中点处,但最高温度与炉膛烟温相差较大,这是由于水冷壁导热性能强和工质的吸热作用。随着鳍片结渣厚度的增加,最高温度区域出现在渣层上,最高温度从鳍片中点处渣表面逐渐扩散至整个渣层表面,由于渣层导热性能差,整个渣层处于高温状态,渣层表面温度趋近于炉膛烟温。根据结渣水冷壁传热原理可知,渣层表面温度越高,渣层表面对炉膛辐射越强,则实际进入水冷壁的热量减少,进而导致水冷壁温度降低,工质换热量减少。

图6 水冷壁截面温度场分布
Fig.6 Temperature distribution of water wall section
2.2 结渣对水冷壁向火侧最高温度的影响
图7、图8分别给出了不同工质对流传热系数和炉膛烟温下结渣厚度对水冷壁向火侧最高温度(位于渣层表面)的影响。随着结渣厚度增加,水冷壁最高温度逐渐升高并趋近于炉膛烟温。当渣层形状由I型转为II型时,渣层表面最高温度与炉膛烟温的差值已小于300 K,转为III型时,渣层表面的温度已接近炉膛烟温。
Thy=1 500 K,ti=600 K

图7 不同工质对流传热系数下水冷壁向火侧最高温度与结渣厚度的关系
由图7可知,工质对流传热系数对水冷壁向火侧最高温度的影响并不显著,αi增大30倍,清洁水冷壁的最高温度仅降低约60 K,一旦结渣并随着渣层增厚,最高温度的差异越来越不明显。表明在不考虑炉膛烟温变化的情况下,当锅炉负荷变化时,水冷壁如果有结渣,αi对渣层表面温度的影响几乎可以忽略。
ti=600 K,αi=25 000 W/(m2·K)
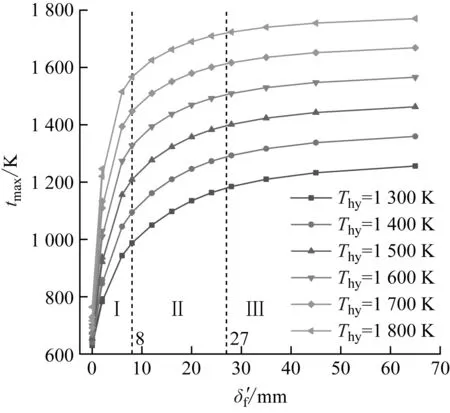
图8 不同炉膛烟温下水冷壁向火侧最高温度与结渣厚度的关系
由图8可知,在清洁水冷壁状态下,炉膛烟温由1 300 K升高到1 800 K时,水冷壁最高温度增幅仅约86 K,而水冷壁一旦结渣,渣层表面的最高温度将随炉膛烟温升高而上升,渣层越厚,其增幅越接近炉膛烟温的增幅。
综合图7和图8可以看出,当水冷壁结渣后,锅炉负荷对渣层表面温度的影响主要在于炉膛烟温的变化,而工质流量变化的影响很小。
2.3 结渣对水冷壁背火侧温差的影响
背火侧三点(管外壁中点A点、背火侧鳍根B点、背火侧鳍片中点C点)两两之间温差随鳍片结渣厚度的变化如图9所示。由图9可知,背火侧温差ΔtAC、ΔtAB和ΔtBC随结渣厚度的变化趋势相似,温差随结渣厚度的增加逐渐减小,温差变化速率也随之减小,最后趋近于一个相对恒定的温度。
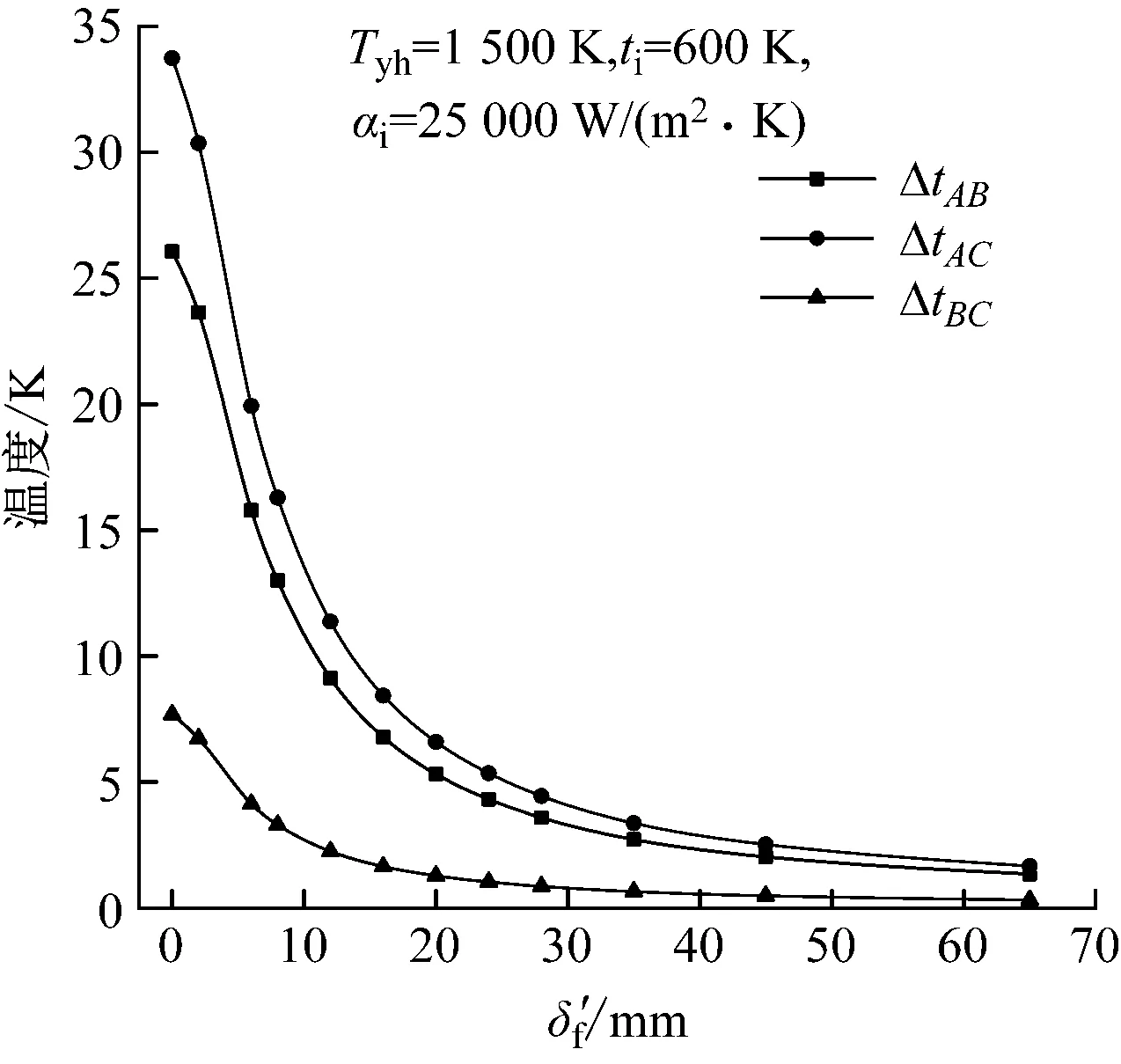
图9 背火侧特定点温差与鳍片结渣厚度的关系
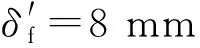
2.4 锅炉运行参数对温差ΔtAC的影响
由结渣水冷壁传热过程可知,除了管子的结构参数外,水冷壁温度场主要与炉内辐射热流密度(由炉膛烟温表示)、管内工质对流传热系数αi和工质温度ti这3个锅炉实际运行参数有关。
2.4.1 炉膛烟温对温差ΔtAC的影响
炉内工况的变化会直接影响水冷壁温度场的变化,其中炉内辐射热负荷的影响最显著。由图10可知,当水冷壁表面清洁时,炉膛烟温对温差ΔtAC的影响比较明显,随着结渣厚度的增加,这种影响逐渐下降。当结渣厚度超过35 mm后,炉膛烟温对温差ΔtAC的影响几乎可以忽略。即使炉膛烟温在很大范围内波动,温差ΔtAC变化幅度仍然很小,最大不超过5 K。此外,由图10还可知,在αi和ti不变的情况下,ΔtAC与Thy均接近线性关系。
ti=600 K,αi=25 000 W/(m2·K)
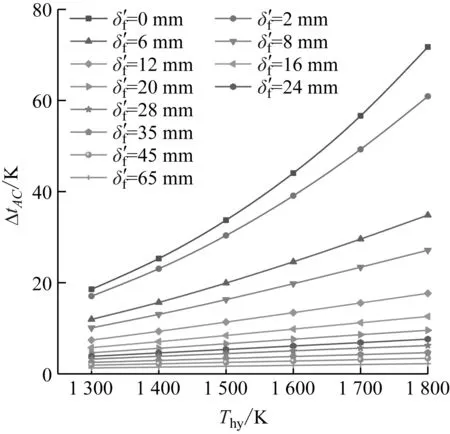
图10 炉膛烟温Thy与温差ΔtAC的关系Fig.10 Relationship between Thy and ΔtAC
2.4.2 管内工质对流传热系数对温差ΔtAC的影响
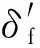
Thy=1 500 K,ti=600 K
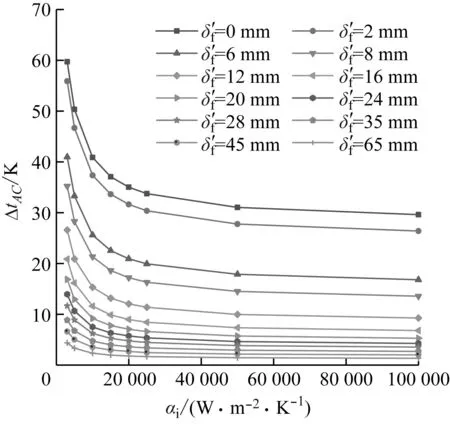
图11 管内工质对流传热系数αi与温差ΔtAC的关系Fig.11 Relationship between αi and ΔtAC
2.4.3 工质温度对温差ΔtAC的影响
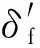
Thy=1 500 K,αi=25 000 W/(m2·K)
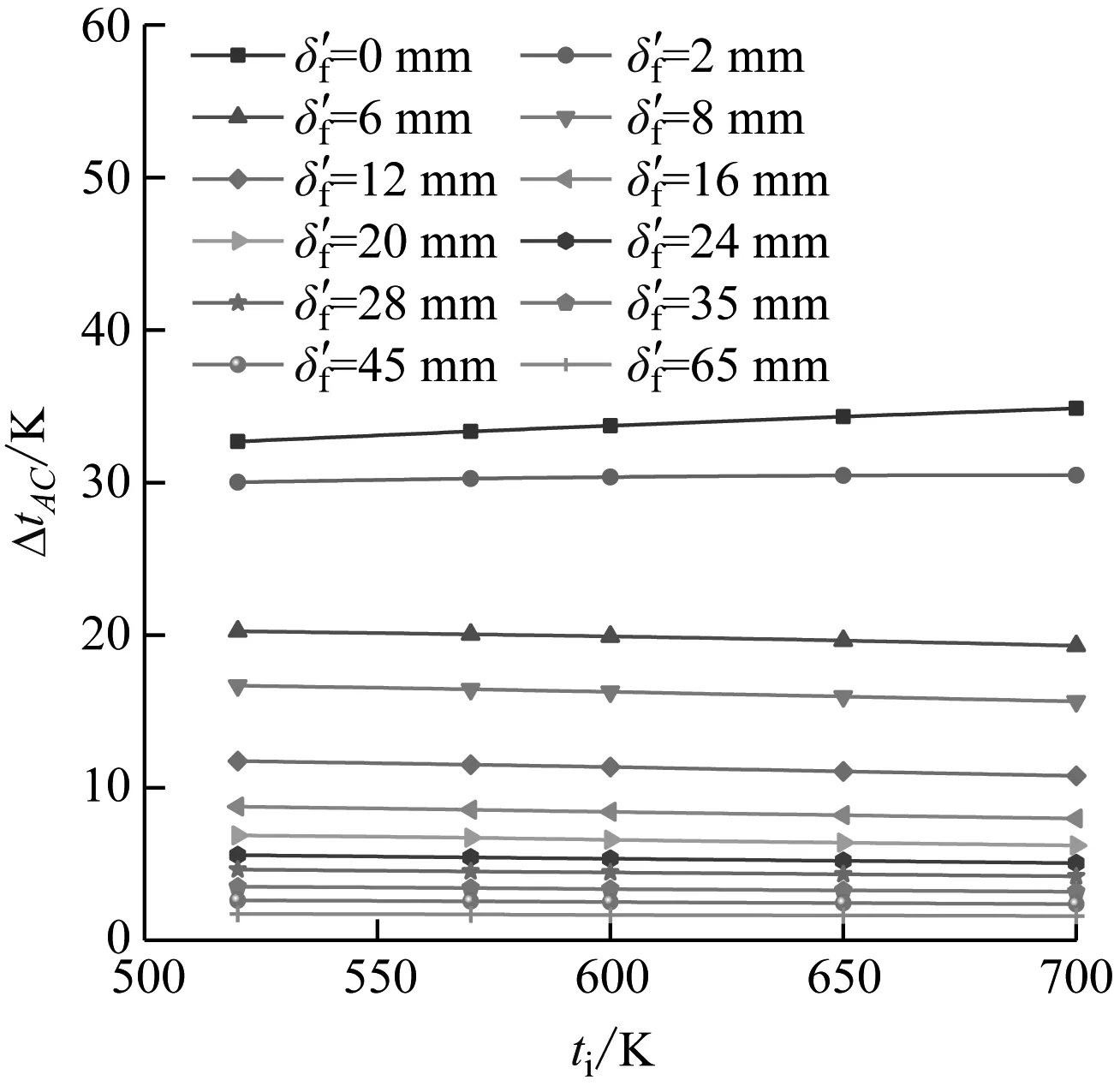
图12 工质温度ti与温差ΔtAC的关系Fig.12 Relationship between ti and ΔtAC
综上所述,对于不同结渣厚度,温差ΔtAC与炉膛烟温呈接近线性正相关关系,且随管内工质对流传热系数的增大而减小,与工质温度关系不大,这与文献[8]等的研究结果相一致,说明考虑结渣增长模型的模拟结果是可行的,相比较而言,本文综合考虑了渣形变化和焊脚结构,所得结果具有更高的精度。
3 结 论
(1) 基于渣层增长模型,研究分析了带焊脚的膜式水冷壁结渣后的温度场分布,发现结渣使得向火侧外表面最高温度由鳍片中点处逐渐扩散至整个外表面,且温度逐渐趋近于炉膛烟温。
(2) 背火侧温差ΔtAC与炉膛烟温呈接近线性正相关关系。当结渣厚度超过35 mm时,炉膛烟温对背火侧温差ΔtAC的影响不再明显。
(3) 背火侧温差ΔtAC随管内工质对流传热系数的增大而减小,并趋近于一相对恒定的温度。锅炉正常负荷范围内,管内工质对流传热系数对背火侧温差ΔtAC的影响小于炉膛烟温。
(4) 与炉膛烟温和管内工质对流传热系数相比,工质温度对背火侧温差ΔtAC的影响很小,基本可以忽略。
