具Holling-III型治疗函数的SEIR模型及其稳定性分析
2021-11-17朱惠延贺芳芳
郭 宇,朱惠延,贺芳芳
(南华大学 数理学院,湖南 衡阳 421001)
simulation
0 引 言
传染病一直影响着人类的健康,据世界卫生组织(world health organization,WHO)报告,全球人口数近一半受到了各种不同传染病的威胁[1]。数学模型对于分析和控制传染病的传播发挥着越来越重要的作用,众多专家、学者通过建立不同的传染病感染模型来了解以及掌握疾病传染的机制,从而为控制病情提出合理的解决方案[2]。
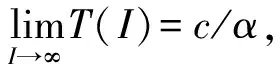
(1)
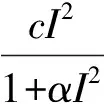
由于模型(1)中前三个方程不含R,因此只需讨论前三个方程:
(2)
模型(2)的初始条件为:
S(0)≥0,E(0)≥0,I(0)≥0。
(3)
1 模型的正定性与有界性
由微分方程理论易知,若模型(2)满足初始条件(3)非负,那么解一定存在,设为(S(t),E(t),I(t))。
定理1 对于任意的t>0,解(S(t),E(t),I(t))非负。
证明:参考文献[14]的方法,将模型(2)的第一个方程转化为:
(4)
(5)
对等式(5)两边从0到t1积分得:
(6)
同理可得
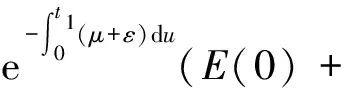
(7)
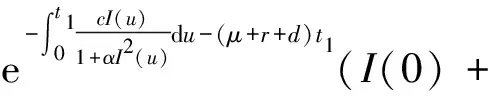
(8)
显然由式(6)知S(t)>0,现考虑E(t)≥0。假设存在时间t′,使得I(t′)=0,I′(t′)<0,当0
0,I(t)≥0,定理1得证。
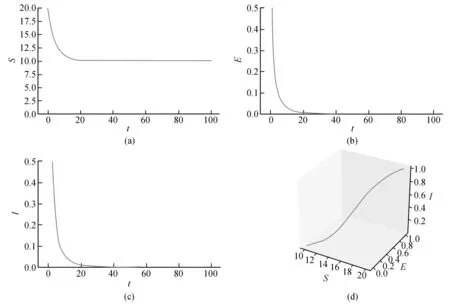
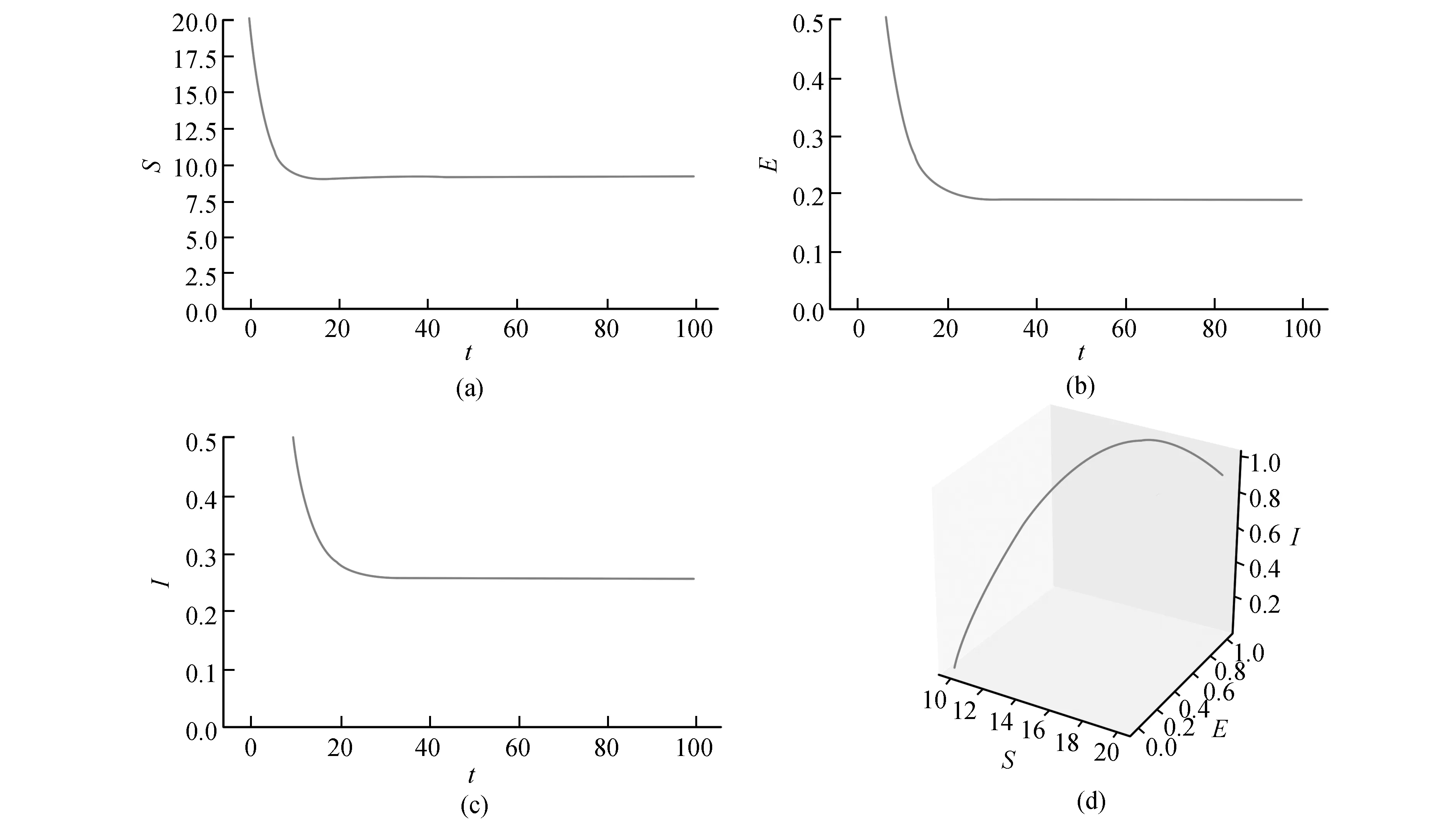
定理2 解(S(t),E(t),I(t))是一致有界的,即存在M>0,使得S(t) 证明:将模型(2)的三个方程相加得: (9) 由式(9)得 (S(0)+E(0)+I(0))e-μt, (10) 设X=(S,E,I)T,将模型(2)表示为如式(11)形式: (11) 其中 求得F(X)与V(X)在无病平衡点处的Jacobian矩阵为: 因此 得到模型(2)的基本再生数为 定理3 当R0<1时,模型(2)中无病平衡点E0是局部渐近稳定的;当R0>1时,E0则不稳定。 证明:模型(2)在E0处的Jacobian矩阵为: 因此特征方程为|λI-J(E0)|=(λ+μ)(λ2+a11λ+a22)=0,其中 a11=2μ+ε+r+d, a22=(1-R0)(μ+ε)(μ+r+d)。 显然,a11>0,λ=-μ<0为特征方程的一个负特征值;当R0<1时,有a22>0,再结合Routh-Hurwitz判据[16]知|λI-J(E0)|=0的特征根均具有负实部,即当R0<1时,模型(2)中无病平衡点E0是局部渐近稳定的;当R0>1时,E0不稳定。 由模型(2)可求得地方病平衡点为: I*为三次方程b11I*3+b22I*2+b33I*+b44=0的正根,其中 b11=α(μ+ε)(μ+r+d)(β+μb), b22=αμ(μ+ε)(μ+r+d)+c(μ+ε)(β+μb)-Αβεα, b33=(μ+ε)(μ+r+d)(β+μb)+μc(μ+ε), b44=μ(μ+ε)(μ+r+d)(1-R0)。 由于参数都为正数,显然b11>0,b33>0。若R0<1,可知b44>0;若R0>1,可知b44<0。因此,模型(2)正根个数由b22,b44的符号决定,下面根据笛卡尔符号准则来判断f(I)=b11I*3+b22I*2+b33I*+b44可能的正根个数。 由表1可以得到如下结论。 表1 方程f(I)=0可能的正根数Table 1 The number of possible positive roots of f(I)=0 定理5 模型(2)的正平衡点有如下几种情况。 (1)当R0<1,b22>0时,模型(2)不存在地方病平衡点; (2)当R0>1,b22>0时,模型(2)存在唯一的地方病平衡点; (3)当R0<1,b22<0时,模型(2)存在零个或两个地方病平衡点; (4)当R0>1,b22<0时,模型(2)至少存在一个地方病平衡点。 定理6 当R0>1且0 证明:模型(2)在E1处的Jacobian矩阵为: 因此特征方程为 |λI-J(E1)|=λ3+c11λ2+c22λ+c33=0, 其中 αI*2)2+c+cI*(2b-αI*)), (b(μ+r+d)(1+αI*2)2+c+cI*(2b- αI*))。 由于b(μ+r+d)(1+αI*2)2+c+2cbI*>2b(μ+r+d)αI*2,因此只要满足2b(μ+r+d)αI*2>cαI*2即c<2b(μ+r+d),M才为正。 显然,当0 下面通过数值模拟对模型(2)所得的稳定性结果进行验证。 1)选取参数值Α=2,β=0.05,ε=0.8,μ=0.2,b=5,c=0.5,α=5,r=0.2,d=0.2,由这些参数值可得模型(2)基本再生数R0≈0.667<1,模型(2)存在唯一的无病平衡点E0(10,0,0),且E0是局部渐近稳定的,结果见图1。 图1 S,E,I的时序图与解的轨迹图(R0<1)Fig.1 Time series of S,E,I of the system and the phase trajectory of the system(R0<1) 2)选取参数值Α=2,β=0.1,ε=0.8,μ=0.2,b=1,c=0.8,α=2,r=0.1,d=0.1,计算得到模型(2)基本再生数R0=2>1,且参数值满足c<2b(μ+r+d),b22=0.08>0,b44<0,此时模型(2)存在唯一地方病平衡点E1(9.081 9,0.183 6,0.253 4),该地方病平衡点是局部渐近稳定的,结果见图2。 图2 S,E,I的时序图与解的轨迹图(R0>1)Fig.2 Time series of S,E,I of the system and the phase trajectory of the system(R0>1) 本文建立并研究了一类具Holling-III型治疗函数的SEIR传染病模型,运用常微分方程稳定性理论对模型进行了稳定性分析。研究发现,在基本再生数R0<1处模型只存在唯一的无病平衡点,且无病平衡点是局部渐近稳定的;当基本再生数R0>1时,此时模型不仅存在无病平衡点,还存在一个或三个地方病平衡点。当出现一个地方病平衡点时,本文给出了该地方病平衡点局部渐近稳定所需的条件。对于出现三个地方病平衡点时的情形,其稳定性分析将是我们未来的研究工作。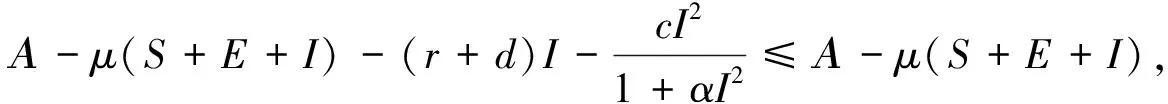
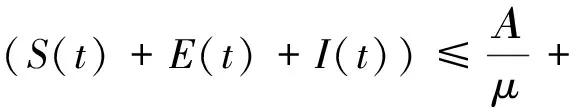
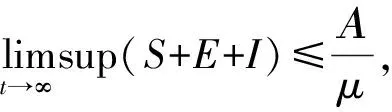
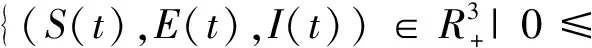
2 无病平衡点与基本再生数
3 地方病平衡点稳定性分析

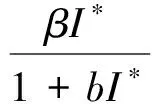
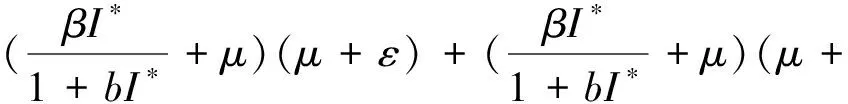
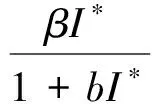
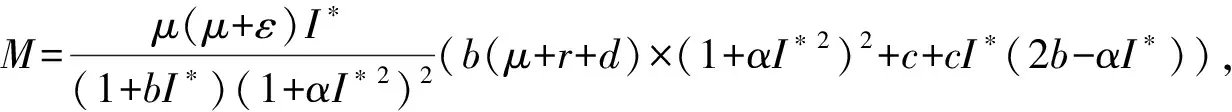
4 数值模拟
5 结 论
