具有双时滞SIRS传染病模型的稳定性与Hopf分支
2021-11-17刘柏林许友军王建伟
刘柏林,许友军,王建伟
(南华大学 数理学院,湖南 衡阳 421001)
0 引 言
传染病是由病毒或其它病原体引起的一类传染性很强的疾病,主要在人与人或人与动物之间互相传播。部分传染病会与人类共存,另一部分则因人们采取措施而消亡。人类曾经发生过大规模流行性传染病,比如流感、天花、黑死病等。人们在长期与传染病抗争的过程中总结出以下经验:感染初期无明显症状,在经过一段时间后表现出相应症状,并迅速以指数式的传播增长。研究初期人们并未考虑到时滞延迟因素,后来研究者们发现引入时滞(单或双时滞)因素,如疾病的潜伏周期,免疫周期等,得到的结果更加逼近实际。不少学者在传染病动力学时滞延迟的研究方面已取得了很多研究成果[1-4],为传染病的防治提供了有效的理论依据。文献[5]中作者研究了一类具有Logistic输入率的双时滞SIRS模型,如(1)所示:
(1)
其中S(t)、I(t)、R(t)分别代表t时刻的易感者人数,感染者人数,及康复者人数。参数r、K、β、α、μ、α1、γ、δ都是正常数。其中r是种群的净增长率,K是理想环境下的最大种群容纳量,β是感染者的平均接触系数,α是与感染者有关的抑制饱和因子影响,μ是种群的自然死亡率,α1是种群的因病死亡率,γ是疾病的康复率,δ是疾病康复后再次复发的概率,τ1是疾病的潜伏周期,τ2是疾病感染者的康复周期。作者全面研究了正平衡点的稳定性,Hopf分支的方向与周期解的稳定性。
在文献[5]基础上,将疾病的发生率函数βSI/(1+αI)修改为βSI/(1+αS),即疾病发生率的抑制饱和因子与易感者有关,再考虑到患者康复后存在一个免疫周期,即有再次感染的风险。因此得到以下模型:
(2)
其中τ2代表疾病的免疫周期,其它参数代表的意义与模型(1)相同。
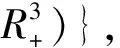
1 正平衡点的局部稳定性与Hopf分支
经简单计算可知,系统(2)总存在一个无病平衡点E0(K,0,0)。由基本再生数的生物学意义,定义系统(2)的基本再生数为:
显然当R0>1时,系统(2)存在唯一的正平衡点E*(S*,I*,R*)。其中
将系统(2)在正平衡点E*处线性化可得到等价系统(3)
(3)
其中
系统(3)对应的特征方程为
λ3+m2λ2+m1λ+m0+(n2λ2+n1λ+n0)e-λτ1+p0e-λ(τ1+τ2)=0,
(4)
其中
情形1 当τ1=τ2=0时,方程(4)为
λ3+m12λ2+m11λ+m10=0,
(5)
其中
m12=m2+n2,m11=m1+n1,
m10=m0+n0+p0。
若方程(5)的系数满足下列条件
(H1)m12>0,且m11m12-m10>0。
由Routh-Hurtitz准则可知,方程(5)的所有根都具有严格负实部。根据泛函微分方程的稳定性理论可得到定理1。
定理1 当τ1=τ2=0时,如果条件(H1)均满足,系统(2)的正平衡点E*是局部渐近稳定的。
情形2 当τ1=0,τ2>0时,方程(4)可写成如下形式
λ3+(m2+n2)λ2+(m1+n1)λ+(m0+n0)+p0e-λτ2=0,
(6)
假设λ=iω(ω>0)是方程(6)的一个纯虚根,代入其中化简得
-iω3-(m2+n2)ω2+i(m1+n1)ω+(m0+n0)+p0(cosωτ2-isinωτ2)=0。
分离实部和虚部得到
两式平方相加得到
ω6+c2ω4+c1ω2+c0=0,
(7)
其中
令z=ω2,则方程(7)变为
z3+c2z2+c1z+c0=0,
(8)
定义函数
f(z)=z3+c2z2+c1z+c0。
(9)
讨论方程(8)根分布情况,由文献[6],得到以下引理:
引理1 对于方程(8)的系数
(i)若c0<0,方程(8)至少有一个正实根;
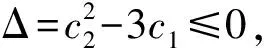
现在假设f(z)的系数满足下列条件
(H2)c0<0或者c0≥0,Δ>0,z*>0,f(z*)≤0。
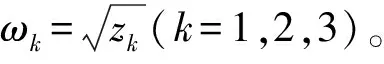
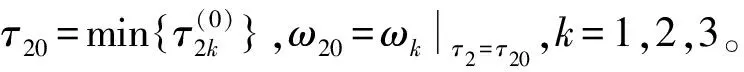
根据Hopf分支理论[7],需要验证横截性条件。设λ(τ)=α(τ)+iω(τ)是方程(7)在τ=τ20处且满足α(τ20)=0,ω(τ20)=ω20的根,下面寻找横截性条件,对方程(6)两边关于τ2求导,得到
因此,有
注意到
显然,当满足下列条件时
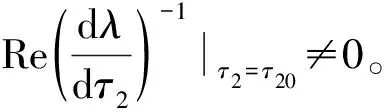
定理2 当τ1=0,τ2>0时,有
(1)若(H2),引理1(ii)成立,则系统(2)的正平衡点E*对所有τ2>0都是局部渐近稳定的;
(2)若(H2),(H3)成立,则当τ2∈(0,τ20)时,系统(2)正平衡点E*是局部渐近稳定的;当τ2>τ20时,系统(2)的正平衡点E*是不稳定的;当τ2=τ20时,系统(3)在正平衡点E*处出现Hopf分支。
情形3 当τ1>0,τ2=0时,方程(4)重写为
λ3+m2λ2+m1λ+m0+(n2λ2+n1λ+n0+p0)e-λτ1=0,
(10)
此时类似情形2,采用相同的研究方法,可得到类似的结论:
定理3 对于τ1>0,τ2=0时,若与(H2),(H3)相对应的条件成立,则当τ1∈(0,τ10)时,系统(2)正平衡点E*是局部渐近稳定的;当τ1>τ10时,系统(2)的正平衡点E*是不稳定的;当τ1=τ10时,系统(2)在正平衡点E*处出现Hopf分支。
情形4 当τ1>0,τ2>0且τ2∈(0,τ20)时。此时系统(3)的特征方程就是方程(4)
λ3+m2λ2+m1λ+m0+(n2λ2+n1λ+n0)e-λτ1+p0e-λ(τ1+τ2)=0
将τ1视为分支参数,令λ=iω(ω>0)是方程(4)的根,代入其中并分离实部和虚部可得
其中
两式平方相加,并展开得到
l1(ω)+2l2(ω)cosωτ2+2l3(ω)sinωτ2=0
(11)
其中
假设
(H4)方程(11)有有限个正根,记这些根为ω11*,ω12*,ω13*,…,ω1k*。
那么对每一个固定的ω1j*(j=1,2,3,…,k),相应的时滞临界值为
记
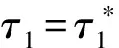
因为
所以有
其中
进一步作代换,有
(12)
其中
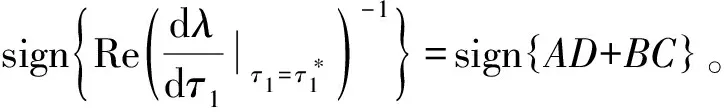
所以只需满足下列条件
(H5)AD+BC≠0。
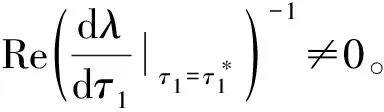
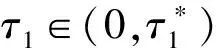
2 数值模拟
参考文献[5]提供的数据,取r=0.02,K=150,μ=0.037 5,α=0.002 5,α1=0.05,β=0.075,γ=0.035,δ=0.042。得到系统(2)特殊系统如下:
(13)
通过计算,可得到系统(13)的正平衡点为E*(1.6400,0.3119,0.1373)。
(1)τ1=0,τ2>0
计算得到τ20≈49.506 4,由定理2知,系统(13)的正平衡点E*在τ2∈(0,τ20)是局部渐近稳定的;在τ2>τ20时不稳定;并在τ2=τ20处发生Hopf分支,详见图1和图2。
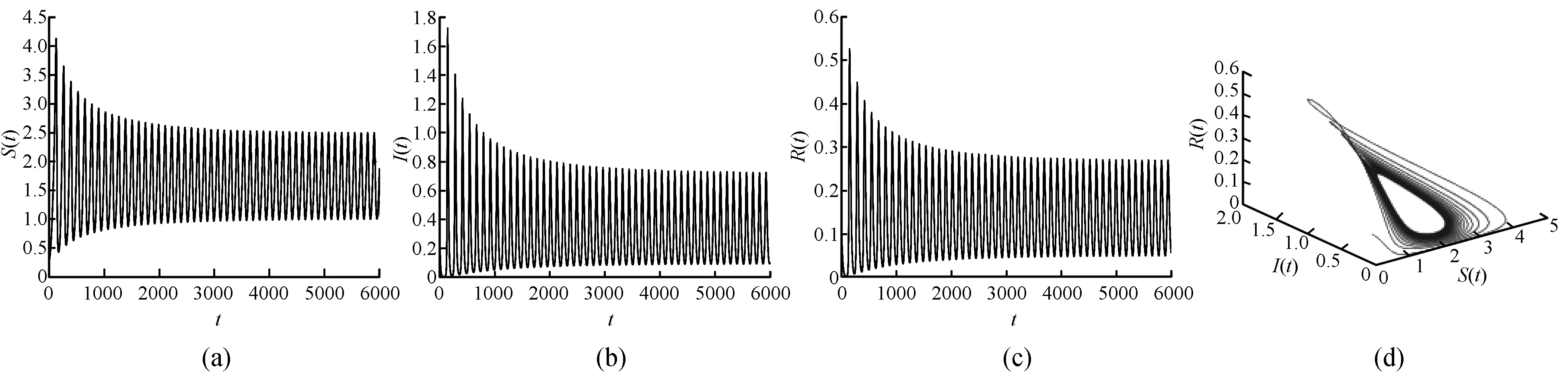
图2 当τ1=0,τ2=60>τ20时,正平衡点E*不稳定Fig.2 E* is unstable when τ1=0,τ2=60>τ20
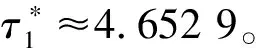

图3 当时,正平衡点E*渐近稳定Fig.3 E* is asymptotically when

图4 当时,正平衡点E*不稳定Fig.4 E* is unstable when
3 结 论
本文研究了一类具有免疫潜伏时滞的SIRS传染病模型,重点讨论了正平衡点的局部渐近稳定性。可以得出当潜伏期时滞较小时,免疫期的时滞影响系统的稳定性;反之当免疫期时滞较小时,潜伏期时滞影响系统的稳定性。关于正平衡点E*的Hopf分支的方向以及分支周期解的稳定性,还有待进一步的研究。
