高中数学教学中核心素养的渗透路径探析

任姣玲

摘要：现行课程标准明确指出，高中教师在教育工作中不能过多遵循以往的学分教育思想，只注重提高学生的考试成绩，而要侧重学生综合素质及核心素养的全面发展。基于这一前提，教师需重构教学体系，创新教学方法，要侧重强化学生的能力，转化学生的意识，为其自身的发展做好稳定铺垫。除此之外，教师也需要重新解读核心素养视角下的教学要求，对固有的教学理念教学体系加以调整。本文将对如何在高中数学教学中渗透核心素养进行分析。

关键词：高中数学;核心素养;渗透路径

核心素养的内涵会因为学科的不同而呈现出一定的差异。数学核心素养主要包括六大要素，分别为数学抽象、逻辑推理、数学建模、直观想象、运算能力以及数据分析。基于这六大要素分析来看，培养学生的核心素养，主要目的在于增强学生的能力。教师需要立足于数学学科，强化学生的问题分析能力、解决能力以及知识应用能力。所以，渗透核心素养时，教师需突破传统学分教育思想的限制，摆脱填鸭式教育的禁锢，打造全新教育体系。

一、加强教材理解，挖掘素养成分

教学并不仅仅是一门工作，更高程度上是一门艺术。在正式开展教学活动之前，教师需要基于教学内容，展开有效的教学设计，借助合理的教学设计，增强整体的教学效果，培养学生的核心素养。可以说，教学设计是教师开展教学活动前需重点推进的一大环节，其具有较高的预设性，对于教学质量也会产生较高的影响。正所谓，教无定法，贵在得法。任何教案都无法适用于所有的课程，所以教师需要基于核心素养，理解挖掘教材的核心素养组成要素，应将教学工作与核心素养培养有效整合。

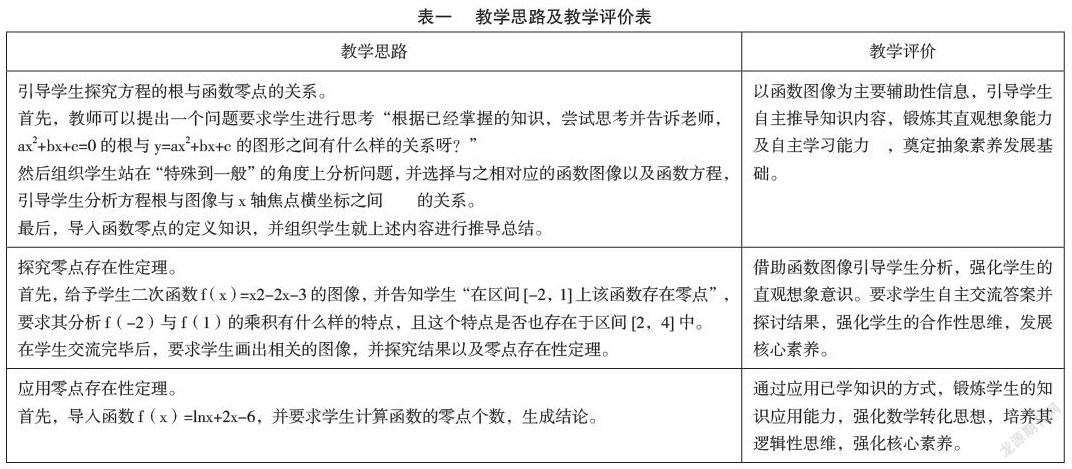
以函数概念與性质这一部分的内容为例。在高中阶段的数学教学中，函数是十分重要的一大模块。掌握函数对于学生能力及素养的发展确有至关重要的影响。以这一大主题中的“方程的根与函数的零点”这一知识点为例。客观分析这一部分的教学内容来看，结合教科书本身，这一部分的教学内容可被划分为三大模块：第一，引导学生探究方程的根与函数零点的关系;第二，探究函数零点存在性定理;第三，探究零点存在性定理的应用。

二、精抓三维目标，凸显素养需求

新课程教学改革任务推行以来，我国陆续提出了三维目标以及核心素养目标。对于长期接受被动教学模式以及传统教学思想的师生群体来说，很容易出现吃不消的情况，甚至有部分教育工作者会认为核心素养目标是在三维目标之后所形成的，所以对于三维目标可以适当忽视。然而事实却正相反。核心素养目标与三维目标之间具有较为紧密的联系，可以说核心素养目标包含着三维目标。所以在核心素养教学视角下，高中数学教师仍旧需要以三维目标为核心要点，借此凸显核心素养对于学生发展所提出的需求，更有针对性地对学生实施教育指导。

针对知识与技能这一目标，教师要加强教学的精细化与详细化。例如，在讲解数学概念时，不能只要求学生死记硬背概念的基本信息，而是要让学生真正理解概念的具体内涵;在讲解数学原理时，不能直接为学生展示数学原理的推导过程，而是要让学生真正体会原理的形成逻辑，理解原理的性质。

针对过程与方法目标，要遵循重理解、重实践、重过程的教学原则，以此充分体现这一目标，切实增强学生的数学能力、数学思维、数学意识，培养学生的核心素养。

针对情感态度与价值观这一目标，要注重微观。与其他两个目标不同，情感态度价值观需要学生在学习过程中间接获取，而无法直接习得。所以，教师要侧重培养学生的学习兴趣，丰富学生的感官体验，在增强学生主体意识的基础上，逐步过渡到情感态度及价值观，促使学生核心素养有机形成。

以“三角函数”这一章节教学为例。在设计三维目标时，教师可以参考如下方式。

首先，知识与技能目标可设定为掌握正弦函数、余弦函数以及正切函数的概念定理，能够基于函数公式解决相关的数学问题。

其次，过程与方法目标可设定为，能够通过类比、推理的方式，证明正弦函数、余弦函数、正切函数之间的关系，强化其自身的逻辑推理能力;通过推导的方式尝试证明正弦定理和余弦定理，强化数学思想。

最后，情感态度与价值观目标可设定为，能感受到函数的美、能够了解三角函数的应用价值、能够形成正确的数学态度。

三、注重过程设计，蕴含核心素养

首先教师要立足于教学思路，展开逆向教学。教师需要站在逆向角度上，根据传统的教学逻辑教学思路，展开反向教学设计。教师要立足于学生的角度，基于教学目标，逆向推导教学内容、教学计划与教学过程，引导学生自主的完成知识建构，在主动获取知识探求知识的过程中，培养学生的核心素养。

以函数的基本性质中“偶函数”这一知识点为例。站在逆向教学角度上分析来看，教师首先需要明确教学目标，也就是让学生掌握偶函数的概念、理解偶函数的内涵，并能够应用偶函数解决一些问题。然后教师可基于逆向推导，思考在教学中所应该提及的问题。例如什么是偶函数？如何知晓偶函数的概念？站在知识迁移的角度上，之前所学习过的哪些知识与偶函数有所联系？在明确这些内容之后，教师便可基于学生的最近发展区，选择学生所熟悉的一些函数图像，如一次函数、二次函数、反比例函数等，逐步切入教学内容。展示完函数图像后，教师可要求学生思考，如何用代数来表示函数上的点的位置。

根据之前所学习过的内容，学生很容易就会想到坐标。之后，教师可以继续引导，在偶函数图像中两个对称点的坐标，有什么样的特点？通过简单的观察，学生会发现对称点的横坐标互为相反数，而纵坐标是相等的。在这些基本教学活动结束后，教师便可抽象性的引导学生进行思考，加深其对于偶函数概念的理解。首先，教师可要求学生思考问题。对于定义在R上的函数f（x），如果f（-5）=f（5），那么这个函数一定是偶函数吗？让学生结合自己对于偶函数的理解尝试性判断，锻炼学生的自主思考能力及分析能力，使之不论是在形的角度上，还是在数的角度上，都能够掌握偶函数的内涵，强化自身的直观能力、抽象能力及逻辑推理能力，奠定核心素养，发展基础。

除此之外，教师需深入挖掘知识的内涵，引导带领学生开展深度学习。虽然数学知识本身并不是核心素养，但其对于学生核心素养的发展却有着至关重要的影响。一旦教师在教学过程中脱离了教学知识本身，那么核心素养的培养便荡然无存。所以，教师需要立足于深度教学，考虑到教学的思维与价值维度，站在统筹角度上实施教学设计，深化学生的认知理解。

必要时，教师也可以引入思维导图这一工具，借助思维导图的直观性、逻辑性特点，帮助学生更好地了解知识内容，构建知识框架，在清晰化教学流程的有机辅助下，强化自身的学习有效性。以平面向量这一部分的内容为例，在完成整体教学活动之后，教师可基于教学内容，引导学生制作思维导图，在导图中罗列出与本单元相关的重点知识。完成这一任务后，教师可鼓励学生按照导图中的内容自发的回应相关知识点，以此辅助其针对性地查漏补缺，提高复习效率，强化自己的知识认知，完善原认知体系。例如在平面向量中共包括四大知识点，分别为平面向量的概念、平面向量的运算、平面向量基本定理及坐标表示、平面向量的应用，而这几大知识点又可被细化成多个不同的小知识点，例如在向量的运算中包括加法减法，实数与向量的積。如若按照常规的教学方式引导学生开展学习活动，极容易导致学生产生疏漏。所以教师可充分发挥思维导图工具的价值，增强学生自主学习的完整性与准确性，促使其核心素养的稳步发展。

四、结语

综上所述，在高中阶段的教育工作中，数学学科的重要性不言而喻。而在现代教学环境中培养学生的核心素养，也是教师应重点推进的一项任务。对此，教师需摆脱传统教学模式的限制，切实解决传统教学模式下所形成的问题。一方面，要加强素材及教材的理解，挖掘核心素养的成分。要重构教学目标，凸显核心素养的教学需求。另一方面，教师要调整教学过程设计，要加强教学手段创新，在良性循环中深化核心素养，促使学生全面发展。

参考文献：

[1]魏彦科.在高中数学教学中培养学生核心素养的策略[J].学周刊，2020（08）：67-68.

[2]冯斌.浅谈高中数学教学中学生核心素养的培养[J].学周刊，2018（30）：90-91.

[3]陈丽.关于高中数学教学中渗透数学核心素养的思考[J].科学大众（科学教育），2018（05）：27.

[4]刘东升.从“素质”到“核心素养”——基于核心素养的高中数学教学探析[J].中学教研（数学），2017（08）：1-3.