基于Matlab的中药主成分分析数学实验教学案例

董鸽 闵建中 陈立范 王宏杰

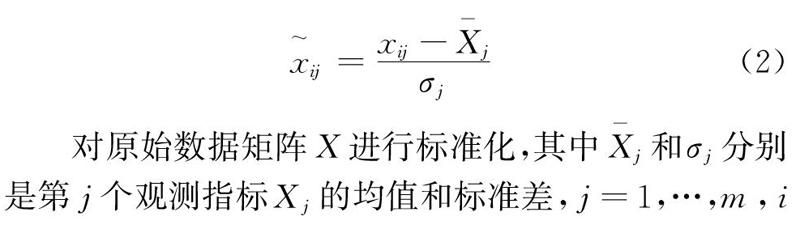
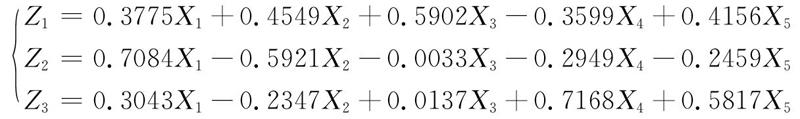
摘 要：本文探讨医学院校数学实验课教学内容与专业相结合的教学案例。以中药专业为例，介绍了中药专业中常用的主成分分析的统计方法，对10批三黄片样品的成分含量进行主成分分析，运用Matlab7.0软件进行计算，给出各主成分与原始成分的线性表达式和因子载荷阵，分析各主成分与原始成分的关联程度以及各主成分在原始成分中所产生的作用，最后运用综合评价函数计算10批样品的F值，根据F值大小进行排序，对10批样品进行综合评价。

关键词：数学实验;案例分析;Matlab;主成分分析

中图分类号：G4     文献标识码：A      doi：10.19311/j.cnki.1672-3198.2021.34.068

高等数学是许多医学专业的必修课程，但理论性强，与专业知识衔接不够紧密。数学实验课程是联系高等数学理论知识与专业实际应用的桥梁，提高学生对高等数学知识的应用能力和计算机技术应用能力，培养学生的科研精神、创新意识和实际操作能力。在医学院校中开始数学实验课，课程内容的选择非常重要，不同的专业对数学知识的需求也不尽相同，因此数学实验的内容也要跟着进行相应调整。以中药专业为例，我们在基础知识的基础上，选择了与中药数理统计的案例，由于篇幅限制，我们仅举例主成分分析模块的数学实验教学案例。

1 主成分分析的步骤

主成分分析是一种降维数据处理的方法，在人脸数据识别、基因数据列分析、食品成分分析、中药成分分析等方面有着重要应用。主成分分析的具体步骤如下：

（1）设原始数据的样本个数为n，有m个观测指标X₁，X₂，…，X_m，其中X_j=（x_1j，x_2j，…，x_nj）^T，j=1，…，m，记矩阵X=（X₁，X₂，…，X_m），欲寻找可以概括m个观测指标综合信息的综合指标Z₁，Z₂，…，Z_m，满足线性组合。

Z_i=a_1iX₁+a_2iX₂+…+a_miX_m，i=1，…，m，（1）

其中：

a_1i，a_2i，…，a_mi为常数，i=1，…，m。

（2）利用公式。

（6）主成分的个数可以按照以下方法确定。

方法一：若主成分的特征值λ_i≥1，则保留该主成分Z_i，否则就去掉。

方法二：若前p个主成分的累计贡献率达到某一特定的值时（例如，以大于90%），则保留前p个主成分。

（7）设已经确定的主成分为Z₁，…，Z_p，选择每个主成分的贡献率c_i作为权重，构造综合评价函数。

F=c₁Z₁+c₂Z₂+…+c_pZ_p（3）

利用公式（1）得到这p个主成分的得分，再代入公式（3）求得每个样品的F值。一般地，F值越大，表明该样品的综合评价效果越好，当然还要根据各主成分的专业意义而定。

2 三黄片成分含量的主成分分析案例

三黄片具有清热解毒，泻火通便的功效。文献利用HPLC 法分析了测定了不同厂家10 批三黃片的大黄素、大黄酚、盐酸小檗碱和黄芩苷的成分含量，运用主成分分析和聚类分析的方法对10批样品的成分含量进行分析评价，为三黄片质量控制提供了依据。在运用主成分分析法时使用的是SPSS 24.0软件，只给出了主成分特征值和贡献率表格以及主成分得分图。本文将采用Matlab7.0软件对文献中10批样品的成分含量进行主成分分析，作为数学实验课教学的案例，给出各主成分与原始成分的线性表达式和因子载荷阵，分析各主成分与原始成分的关联程度以及各主成分在原始成分中所产生的作用，并运用综合评价函数计算10批样品的F值，根据F值大小进行排序，对10批样品进行综合评价，反映药品质量的高低。

我们采用文献的表1中来自不同厂家的10批三黄片的大黄素、大黄酚、大黄素和大黄酚总量、盐酸小檗碱、黄芩苷五个成分含量测定数据作为原始数据，构成10行5列的矩阵，记作X。利用公式（2）对该矩阵进行标准化处理，得标准化之后的矩阵，记作SX，并求出其相关系数矩阵C.Matlab程序如下：

X=[0.61 1.28 1.89 4.02 14.33;

0.57 1.35 1.92 4.60 13.89;

1.03 1.56 2.59 5.85 17.53;

0.98 1.51 2.49 5.50 18.02;

0.50 1.96 2.46 5.26 15.97;

0.51 1.89 2.40 5.43 16.24;

0.64 1.77 2.41 4.85 20.21;

0.63 1.69 2.32 5.13 21.23;

0.46 1.36 1.82 9.07 16.05;

0.42 1.29 1.71 8.89 15.77];

m=size（X，1）;

n=size（X，2）;

SX=zeros（m，n）;

for i=1：b

SX（：，i）=（X（：，i）-mean（X（：，i）））/std（X（：，i））;

end

接著计算矩阵C的特征值与特征向量，Matlab程序为：

C=corrcoef（SX）;

[V，D]=eig（C）;

xlswrite（'D'，D）

xlswrite（'V'，V）

程序中的D为矩阵C的特征值，V为对应的特征值向量。矩阵的特征值具体为λ₁=2.6938，λ₂=1.0168，λ₃=0.8805，λ₄=0.4089，λ₅=1.11e-16。

计算主成分的累计贡献率，Matlab程序如下：

for j=1：n

DD（j，1）=D（n+1-j，n+1-j）;

end

for i=1：n

DD（i，2）=DD（i，1）/sum（DD（：，1））;

DD1（i）=DD（i，1）;

DD（i，3）=sum（DD1（1：i））/sum（DD（：，1））;

end

T=0.9;

for k=1：n

if DD（k，3） >=T

num=k;

break;

end

end

m1=size（V，1）;

PV=zeros（m1，num）;

for j=1：num

PV（：，j）=V（：，n+1-j）;

end

num

PV

DD

将上述程序运行后得到num=3，这表明前3个主成分的累计贡献率大于90%。DD的第1、2、3列分别为特征值、贡献率、累计贡献率。由DD的第3列可以看到，前3个主成分的累计贡献率已经达到91.82%，因此保留了前3个主成分信息。PV运行的结果表示矩阵C特征值λ₁～λ₃对应的三个单位正交特征向量，将其代入公式（1）得到前3个主成分的线性表达式为：

其中变量X₁～X₅分别为大黄素、大黄酚、大黄素和大黄酚总量、盐酸小檗碱以及黄岑苷的含量。可以看出主成分1中大黄素、大黄酚、大黄素和大黄酚总量及黄岑苷的系数都大于0，与主成分1正相关，盐酸小檗碱的系数小于0，与主成分1负相关;主成分2只有与大黄素与主成分2正相关，其余都负相关;主成分3除了与大黄酚负相关，其余都正相关。

运行下列运算程序可得到因子载荷矩阵Q：

Q=zeros（m1，num）;

for i=1：n

for j=1：num

Q（i，j）=PV（i，j）*sqrt（DD（j，1））;

end

end

Q

因子载荷矩阵Q的运行结果见表1，前3个主成分与原始成分的因子载荷阵如表1所示。主成分1中盐酸小檗碱的因子载荷小于0，对主成分1产生负向影响，其余都大于0，大黄素、大黄酚、大黄素和大黄酚总量、黄芩苷这四个原始成分对主成分1产生正向影响。大黄素和大黄酚总量的因子载荷为0.9686，为高度相关，说明与主成分1的联系密切程度非常高。大黄素、大黄酚、黄芩苷与主成分1显著相关，说明与主成分1的联系密切度高。盐酸小檗碱的因子载荷为-0.5906，为显著负相关。可见主成分1越大时大黄素、大黄酚和黄岑苷的含量也越高，而盐酸小檗碱的含量越低。

主成分2中大黄素的因子载荷大于0，对主成分2产生正向影响，其余都小于0，大黄酚、大黄素和大黄酚总量、盐酸小檗碱、黄芩苷这四个原始成分对主成分2产生负向影响。大黄素的因子载荷为0.7144，与主成分2显著相关，说明与主成分1的联系密切度高。大黄酚的因子载荷为-0.5971，与主成分2显著负相关。可见主成分2越大时大黄素的含量越高，大黄酚、盐酸小檗碱和黄岑苷的含量越低，而且大黄素和大黄酚总量越小。

主成分3中大黄素、大黄素和大黄酚总量、盐酸小檗碱和黄岑苷的因子载荷都大于0，这三个原始成分对主成分3产生正向影响，大黄酚的因子载荷小于于0，对主成分3产生负向影响。盐酸小檗碱、黄芩苷的因子载荷分别是0.6726、0.5458，与主成分3显著相关，说明与主成分3的联系密切度高。可见主成分3越大时大黄素、盐酸小檗碱和黄岑苷的含量越高，大黄酚的含量越低，但大黄素和大黄酚总量仍然越大。

根据公式（1-3）计算综合评价函数F， 并进行排序， Matlab程序如下：

score=SX*PV;

for i=1：m

F（i，1）=score（i，：）*DD（1：3，2）;

F（i，2）=i;

end

Fscore=[score， F];

disp（'各主成分得分、F值及排序（按第4列的F值进行降序排列，前3列为个各成分得分，第5列为三黄片的品种）。

F_sort=sortrows（Fscore，-4）

运行程序后可得到不同生产厂家的各成分的F值，并进行排序，结果见表2。三黄片10批样品从高到低的排序的编号为：S3、S4、S7、S8、S5、S6、S1、S2、S9、S10。可以看出S3、S4的F值比较接近，S7和S8的F值接近，S5与S6的F值接近，S1、S2的F值接近，S9、S10的F值接近，这与文献聚类分析的结果一致。S3-S8的F值都大于0，说明样品的品质较高。最后可以根据样品的编号再确定对应实际厂家所生产的三黄片的质量。

3 结束语

数学实验是联系数学知识和医学问题的桥梁，通过数学软件把数学基础理论知识、计算机技术和医学实际问题有效的结合，能够激发学生的学习兴趣，培养学生的应用能力，如何更好地开展医学院校的数学实验课程教学是我们将不断探索的问题。

参考文献

[1]董鸽，徐方勤.浅谈与计算机专业相结合的高等数学教学改革[J].科教文汇，2018，（4）：67-69.

[2]Hui Zou，Trevor Hastie，Robert Tibshirani.Sparse Principal Component Analysis[J].Journal of Computational and Graphical Statistics，2006，15（2）：265-286.

[3]Hancock P，Burton A，Bruce V.Face processing：human perception and principal components analysis[J].Memory and Cognition，1996，（24）：26-40.

[4]Carly L.Clayman，Satish M.Srinivasan，Raghvinder S.Sangwan，K-means Clustering and Principal Components Analysis of Microarray Data of L1000 Landmark Genes[J].Procedia Computer Science，2020（168）：97-104.

[5]張婷，刘慧琴，郭勤卫，等.十六份辣椒材料游离氨基酸组成的主成分分析与聚类分析[J].浙江农业学报，2021，33（4）：640-650.

[6]崔新刚，王颖莹，王新胜，等.基于主成分分析和聚类分析的不同厂家三黄片质量分析[J].中国民族民间医药，2020，29（16）：36-40，43.

[7]史周华，张雪飞.中医药统计学[M].北京：科学出版社，2009.

基金项目：2020年上海健康医学院师资百人库计划项目“统计方法在中草药分析中的应用”（B3020020311084）。

作者简介：董鸽（1980-），女，汉族，江苏泰州人，理学博士，上海健康医学院副教授，主要从事数学教学研究。