借助数轴，显现估算推理本质

杨红娟

摘 要：《用乘法估算解决问题》是本次优质课比赛课例，在研究中发现估算的取值和估算的区间范围的确定是教学的难点，围绕这两个方面，利用数轴剖析难点，分成以下四个步骤：“数轴直观显示，区别乘法估算与加法估算”“数轴自主验证，理清估算策略推理本质”“数轴动态重合，直面估算区间的形成”“数轴判断相同，结合数量关系判断结论”。通过数轴的步步为营，解决了估算的策略选择在于问题要求和比较数据，取值区间在于把估算数估成相邻的整十数，突破区间寻找方法的缺失问题。

关键词：乘法估算;数轴;估算策略;取值区间

在学习乘法估算解决问题之前，学生对估算具备一定学习基础：了解近似数，会用“估算比答”进行加减法的估算。因此本课的重点和难点在于，根据问题情境对估算数据进行合理取值和确定估算的区间范围。但是学生往往无法说清估算的策略选择，且对估算取值的区间认知模糊，缺失寻找区间的方法。根据学生已具备的用线段图分析问题、解决问题的能力，笔者利用数轴（类同线段图）的直观性，帮助学生凸显估算的推理过程，进而判断取值策略的正确性，确定估算准确值的区间范围。

一、数轴直观显示，区别乘法估算与加法估算

由于学生此前对估算的学习是在加减法的基础上进行的，因此学生会把这个方法迁移到本课的估算中，往往会把所有数据全部估大或者全部估小，导致估算结果过大而无法做出正确的判断。笔者分别在尔仪小学302班和303班（共计：81人）试教过程中，以人教版数学三年级上册第六单元的例7为例：三（1）班29个学生去参观航天航空展览，门票8元/人，带250元买门票够吗？学生估算的具体数据情况如表1：

从统计表中可知，有[13]的学生出现了加减法估算方法的负迁移，做判断时出现两种情况：一是根据估算数据结果，得出250元不够的结论;二是根据数感，忽略估算结果，认为250元足够了。前后试教过程，笔者在反馈学生作品做出不同的安排：第一次没有加入数轴，第二次加入了数轴。这凸显了乘法估算和加法估算的区别。

【前期试教片段一】

1. 呈现例题

2. 学生独立估算。师：请你估一估、算一算，写在学习单上。

3. 学生反馈作品

作品一：

估：29≈30

算：30×8=240（元）

比：29×8<240<250

答：250元买门票够了。

（1）学生汇报，规范估算表达的语言。

（2）认识“≈”，区分“≈”和“=”的不同点。

小结：所以可以知道29×8肯定小于240元，也就小于了250元。

作品二：

估：29<30，8<10

算：30×10=300（元）

比：29×8<300（元）

答：250元不够。

请仔细阅读作品二，你认为正确么？理由是什么？

小结：把29×8，如果估算29成30，8估算成10，确定小于300元，但29×8在250元的左边还是右边呢？无法判断29×8和250元的关系，也就无法解决问题。

4. 对比：对比两幅学生作品，你发现了什么？

小结：选择数据估算的时候，要根据问题的要求，有时候可以两个数据都估算，有时候只能估算一个数据。

在本次试教过程中，发现学生虽然知道不能将估算得到的300元和问题的250元进行比较，但是对其中的推理过程依然不明就里，因此笔者在第二次试教过程中，在两次作品反馈之后，结合数轴进行了推理验证。

【定稿教学片段一】

前面教学内容与试教内容一致，在后面加入数轴验证环节。

1. 作品一的数轴验证

小结：从这幅数轴图中可以看出29×8肯定小于240元，也就小于了250元。

2. 作品二的数轴验证

小结：从数轴图来看，把29×8，如果估算29成30，8估算成10，确定小于300元，但29×8和250都在300的左邊，因此无法判断29×8和250元的关系，也就无法解决问题。

追问：什么样的问题，两种做法都可以解决呢？（带300元买门票够吗？）

通过线段图对比，让学生感悟选择数据估算，有时候要选择一个，有时候要选择两个，这是由问题决定的。

二、数轴自主验证，理清估算策略推理本质

由于第一个环节学生已经通过估大的策略确定了带250元购买门票够了，接下来以“那150元钱够买门票吗？”的问题，引导学生利用估小策略解决问题。

【前期试教片段二】

反馈学生的作品

作品一：

估：29≈20

算：20×8=160（元）

比：29×8>160>150<250（元）

答：150元买门票不够。

作品二：

估：29≈30

算：30×8=240（元）

比：29×8<240（元）

答：150元买门票不够。

小结：乘法估算的时候要把数据估算的结果尽量靠近比较的数值，以比较的数值为目标问题的要求合理选择估算的策略。

在教学过程中，先通过学生独立估算。但由于第一环节的影响，部分学生依然会用估大的策略来解决，然后对估大策略和估小策略辨析判断，反馈中，学生感受到了语言表达估算推理的困难。因此，笔者结合学生作品，引入数轴，让学生自己在数轴上摆一摆每个数或者算式的位置，理清估算策略中蕴含的推理本质。

【定稿教学片段二】

前面教学内容于试教内容一致，在后面加入数轴验证环节。

生1：第一幅线段图的29×8大于160元，在160元的右边，也就在150元的右边，所以带150元肯定不够。

生2：第二幅线段图的29×8小于240元，在240元的左边，但是无法判断29×8和150元的关系，所以不知道带150元到底够不够。

小结：乘法估算的时候要把数据估算的结果尽量靠近比较的数值，以比较的数值为目标问题的要求合理选择估算的策略。

因为学生感受到用语言表达推理过程的困难，因此顺理成章的用数轴的直观性来帮助辨析和判断，进而理清估算策略推理本质。最后通过数轴的对比分析得出估算的小窍门：把数据估算的结果尽量靠近比较的数值。同时估算策略选择的方法：以比较的数值为目标和问题的要求合理选择估算的策略。

之后在练习中再次呈现不同情境下的类似估算策略选择问题，并用数轴再次验证估算推理的本质。

【定稿教学片段三】

过渡：已经确定了宇航员模型的价格在300和360元之间，那么带360元肯定是够的，但是估算的过程应该是怎样呢？

1. 请仔细阅读，思考选择A还是B，并想一想、说一说你的理由。

例1：火箭模型的价钱是54元，宇航员模型的价钱是火箭模型的6倍，小明带了360元钱，买一个宇航员模型，够吗？（A）

A：

估：54≈60

算：60×6=360（元）

比：54×6<360

答：360元够了。

B：

估：54≈50

算：50×6=300（元）

比：54×6>300

答：360元够了。

2. 用线段图来验证。

生1：第一幅线段图的54×6小于360元，所以带360元肯定够了。

生2：第二幅线段图的54×6大于300元，在300元的右边，但是无法判断54×6和360元的关系，所以就不知道到底带360元够不够。

3. 小结：比较的数值为目标进行估算，但是也要考虑问题的要求，合理选择估算的策略。

这一点是本课的重点之一，在练习题中让学生以选择题的形式选择合适的估算策略，然后用数轴解释所选择估算策略的推理过程，证明估算策略选择的正确性。

三、数轴动态重合，直面估算区间的形成

学生分别经历了估大和估小策略，在此基础上进行对比，对比的作用有两个：一是学生感悟的问题情境不一样，要解决的问题不一样，选择估算的策略也不一样，有时候估大、有时候估小。二是把线段图通过课件动态演示重合在一起，让学生直面估算的取值区间，即在150到250之间，也在通过估算得到的160到240之间。

【定稿教学片段四】

1. 对比，感悟合理选择估大或者估小的策略。

三（1）班有29名同学去参观航天航空展览，门票8元/人。

带了250元买门票够吗？

估：29≈30

算：30×8=240（元）

比：29×8<240<250

答：带250元买门票够了。

带了150元买门票够吗？

估：29≈20

算：20×8=160（元）

比：29×8>160>150

答：带150元买门票不够。

师：这两道题目和解题方法有什么不一样的地方？（一个估大，一个估小）

小结：所以我们在用估算解决问题的时候，要认真分析具体问题和数据，合理选择估大或者估小的策略。

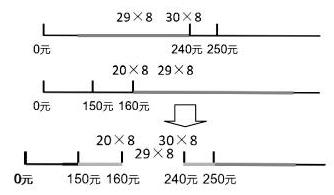
2. 重合线段，感悟估算的取值区间。

师：请仔细看，两幅线段图合成了一幅线段图，看合成的线段图，你有什么发现？

生1：29×8在150元和250元之间，就是灰色部分。

生2：29×8在160元和240元之间，就是白色部分。

小结：是的，通过估算把29估大成30得到了240元，29估小成20得到了160元，就确定29×8的取值区间，即在150到250之间，更在160到240之间。

線段图的动态重合，直观呈现了区间的产生过程，把原本模糊的取值区间明朗化，一下子呈现在学生的面前，通过观察直接得出了29×8的取值区间是怎么来的，是把29估大成30得到240元，29估小成20得到160元，得到区间在160到240之间，完全不需要教师的介入讲解寻找估算取值区间的方法。

在此基础上，直接进行模拟练习。

【定稿教学片段五】

过渡：参观途中，小明看到有关航天航空的模型售卖处，里面有什么呢？我们一起来看看。

选一选：火箭模型的价钱是54元，宇航员模型的价钱是火箭模型的6倍，下面哪个数轴能表示宇航员模型价格范围（B）

（1）请你仔细阅读，并想一想你选择的理由。

（2）小结：把54估小成50得到300元，估大成60得到360元，所以可以确定它的积肯定在300到360之间。

取值区间的练习直接放在线段上选择，这样的形式巩固了估算取值区间的寻找方法，同时对估算区间有了更加清晰的认识

四、数轴判断相同，结合数量关系判断结论

数轴的应用在很大的程度上帮助学生解决很多同类型的估算问题，但是最后教材中安排的“做一做”却与例题的估算结论的判断方法完全不同。在利用数轴帮助判断不适用时，可以结合根据数量关系式来判断得出结论。

【定稿教学片段六】

过渡：参观结束了，大家准备乘坐汽车返校了，在停车场，碰到了四年级的同学也要坐车回去。

例2：360名四年级学生准备返校，一辆车最多能坐54人，6辆车坐得下四年级的学生吗？

（1）学生独立计算

估：54≈60

算：60×6=360（人）

比：54×6<360

答：坐不下360人。

（2）线段图验证

（3）小结：根据线段图来看，54×6小于360人，在360人的右边，人数大于汽车的座位数，所以360人肯定不坐不下。

对比：感悟结论的不一致

问题：请仔细对比例1和例2，有什么相同的地方和不同的地方？

相同点：同样的数据：54、6、360，同样的估算策略：都是估大。

不同点：问题情境不一样，结论也不一样。

小结：虽然数据一样，估算策略一样，但由于具体情境不一样，得到的结论也不一样，所以对于结论的判断，要根据实际情况进行判断。

在对比中，相同的数据、相同的数轴，但得到的结论判断完全不一样，让学生感受到有时候数轴不是万能的，存在一定局限性。面对估算“每份数”和“份数”引起的估算结论判断的不同，直面估算的难点。在例题的学习中，以估算“份数”为主，让学生产生了“估小了不够肯定不够，估大了够肯定就够”的错觉，而教材中安排的“做一做：估算‘每份数”就打破了这个错觉。因此，笔者直击这个矛盾点，用相同的数据，不同的问题情境，引导学生感受估算“份数”和“每份数”，得出的结论完全相反。进而引导学生要根据问题的情境做出合理的判断，实际情况实际分析。

五、结语

通过数轴的步步为营，从根本上让学生感悟到估算的策略选择要根据问题要求和比较数据来确定，取值区间的确定在于把估算数估成相邻的整十数，并且利用数轴突破区间寻找方法的缺失问题。最后在面对估算“每份数”和“份数”引起的估算结论判断的不同，直面估算的矛盾点，引发学生的思考，得出要根据问题的情境做出合理判断的结论，给这节课画下圆满的句号。