基于MSVAR 模型的非线性损伤识别方法
2021-11-12段忠东欧进萍
郑 泓,段忠东,欧进萍
(哈尔滨工业大学(深圳)土木与环境工程学院,深圳 518055)
土木工程结构(如大跨桥梁、超高层建筑等)在服役过程中难免会出现损伤,严重时甚至会导致结构失效而引发灾难性事故,因此有必要对结构的损伤状态进行监测[1-4]。传统的无损检测技术需要预知损伤位置,对检测设备难以到达的位置存在盲点,而且过于依赖巡检人员的既有经验和主观判断[3]。为克服传统方法的不足,基于振动的损伤识别方法开始受到学者们的关注[4-5]。这类方法通常需要借助线性模型对结构振动响应进行建模,提取与损伤相关的模型参数(如模态频率等)作为损伤敏感特征,通过比较损伤前后这些特征的变化实现损伤识别。
实际工程中出现的损伤往往具有一定的非线性特征[6-7],比如裂缝的开合效应导致结构响应出现非平稳特征[8];结构在地震作用下的塑性耗能使得恢复力曲线形成近似封闭的滞回环[9]。采用线性模型不仅无法获取损伤的真实信息,而且极易受到其他非线性因素的干扰,导致损伤预警的精度和可信度不高。以模态频率为例,环境温度变化对模态频率的影响往往大于损伤的影响[10-12]。因此,有必要引入非线性分析的方法,通过准确获取损伤的非线性信息提高损伤识别方法的工程适用性。
非线性损伤识别主要分为非线性指标方法和非线性系统识别方法两大类[6]。其中,基于非线性指标的方法认为损伤会导致结构响应出现非线性特征,借助能够表现数据非线性变化的指标实现损伤预警。该方法具有建模方便,易于实现在线监测的优点,已成为非线性损伤识别的研究热点。Robertson 和Farrar 等[13]认为非线性损伤的出现会导致结构响应产生突变,利用Holder 指数跟踪结构响应信号的不连续性实现损伤监测。Chen和Yu[14]结合自回归滑动平均模型(ARMA)和广义自回归条件异方差模型(GARCH)对结构加速度响应进行建模,定义模型残差的标准差作为损伤敏感特征,通过试验表明采用非平稳时间序列模型能够增强损伤识别的准确性。Yu 和Zhu[15]对结构振动响应建立自回归模型(AR),利用模型残差的高阶矩识别非线性损伤。马家欣和许飞云等[16]将带有外部输入的非线性自回归模型(GNARX)应用于钢板的损伤识别,发现其识别效果优于线性时间序列模型。Li 和Sun 等[17]通过计算结构自由响应信号的互相干矩阵识别结构非线性损伤,克服了传统基于相干函数的非线性损伤识别方法需要测量激励信号的缺点。Chen 和Yu 等[18]为解决ARMA 模型无法处理非线性损伤识别的问题,构造向量空间余弦相似度作为损伤敏感特征,然后利用K 均值聚类和贝叶斯判别实现非线性损伤的快速预警。
在非线性系统识别领域中,损伤模型用于描述不同类型损伤对结构物理特性(主要是刚度和阻尼)的影响,比如土木工程结构中较为常见的损伤裂缝用双线性刚度模型表示。上述基于非线性指标的方法把关注点放在“是否出现非线性损伤”,忽略了损伤非线性特征的差异性,无法识别损伤类型。基于非线性系统识别的方法采用不同损伤模型对结构响应进行建模,以最小建模误差作为确定损伤类型的标准。该方法在建模上需要消耗大量时间[19],不适合结构在线监测,而且识别损伤类型之前仍然需要判断结构是否出现非线性损伤。因此,本文结合非线性指标方法和非线性系统识别方法的优点,提出基于马尔科夫区制转移向量自回归模型(MSVAR)的非线性损伤识别方法,并通过数值算例和模型试验验证本文所提方法能够有效识别裂缝损伤。
1 MSVAR 模型理论
MSVAR 模型属于非线性时间序列模型,最早用于挖掘经济行为的内在机制,比如国民生产总值受政策影响而产生的增长期和衰减期[20]。
对于满足零均值但非平稳的l维时间序列Yt∈Rl×1(t=1,2,···,T),MSVAR 模型描述这样一个数据过程[21]:Yt受m个机制影响,相同机制下的数据用同一个p阶向量自回归模型(VAR)描述;数据在不同机制之间的转换采用马尔科夫链表示。上述MSVAR 模型简写成MS(m)VAR(p),用公式表示为:

MSVAR 模型采用隐状态平滑概率表征数据过程处于某一种隐状态的可能性大小,在实际应用中可通过隐状态平滑概率的改变判断研究对象在何时出现状态改变。在计算平滑概率前,需要采用极大似然法估计MSVAR 模型参数[21]。假设式(1)中Yt取自隐状态i的条件概率满足多维正态分布,即:

式中:符号 (÷) 代表两个向量对应元素相除;ξt|T的第i个元素代表第i个隐状态在t时刻出现的概率。
2 非线性损伤预警原理
非线性损伤指标法假设损伤会导致结构振动响应出现非线性特征,即结构从线性系统转变成非线性系统的预示着损伤的出现。考虑到环境激励下线性系统的振动响应可用VAR 模型表示[22-24],所以采用MSVAR 模型对响应数据进行建模会出现两种情况:第一种是MSVAR 模型某一隐状态的平滑概率始终为100%,表明数据过程只受一种机制作用,MSVAR 模型退化为线性的VAR 模型,结构不存在损伤;第二种是MSVAR 模型有多个隐状态的平滑概率大于零,说明采用非线性的MSVAR 模型才能准确描述结构振动特征,即结构出现损伤。

采用四阶龙格库塔法计算振子在白噪声激励下的响应,以100 Hz 采样频率采集其位移数据进行分析。如图1 所示,该单自由度振子由小幅简谐振动过度到幅值较大的简谐振动。其中,过度阶段(2 s~3 s)响应幅值逐渐增大的原因是 |x|<1导致系统阻尼为负。

图1 线性系统到非线性系统的位移响应时程Fig. 1 Time history of displacement response from linear system to nonlinear system
对生成的400 个位移响应数据建立MS(3)VAR(2)模型,其隐状态平滑概率时程如图2 所示。前2 s 隐状态2 和隐状态3 的平滑概率均为0,MSVAR 模型退化为隐状态1 对应的VAR 模型,说明结构响应可以采用线性模型进行建模;2 s后隐状态1 的平滑概率为0,隐状态2 和隐状态3的平滑概率都存在大于零的时刻点,说明采用简单的线性VAR 模型已经不能准确描述结构真实振动状态,结构由线性系统转为非线性系统。
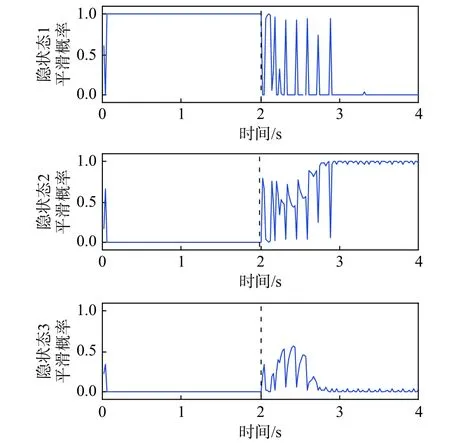
图2 线性系统到非线性系统的平滑概率变化Fig. 2 Changes of smooth probabilities from linear system to nonlinear system
为实现损伤预警,本文引入信息熵作为非线性损伤的预警指标,其表达式[27]为:

3 裂缝类型损伤的识别方法
判断结构出现损伤后需要对损伤类型进行识别,并进一步确定损伤位置和程度。因为不同类型的损伤对应不同的数学模型[6],本节根据MSVAR 模型与双线性刚度系统的等价关系,阐述识别裂缝类型损伤的思想。
3.1 双线性刚度系统的MSVAR 模型
双线性刚度系统最极端的例子是碰撞振子,该系统对应于一个球对着一面刚性墙壁的碰撞。在土木工程领域中,与碰撞振子类似的是带有裂缝损伤的结构[28],以单自由度系统为例,其运动方程为:

3.2 损伤类型识别
裂缝的张开和闭合导致结构在两种不同的振动状态来回切换,对应的MSVAR 模型也会出现两个隐状态交替激活的现象,即平滑概率时程在0 和100%两个值之间切换。
以3 自由度矩形截面悬臂梁为例展示裂缝损伤对隐状态平滑概率影响的特殊性,其振动微分方程为:

根据截面惯性矩定义可知,式(15)表明裂缝张开时裂缝位置悬臂梁的有效横截面积约为裂缝闭合时的85%。
同样,采用四阶龙格库塔法计算上述悬臂梁在白噪声激励下的振动响应,以50 Hz 采样频率收集200 个位移数据建立MS(3)VAR(2)模型,各隐状态的平滑概率时程如图3 所示。从图3 可以看出,MSVAR 模型只有隐状态1 和隐状态2 被激活,与裂缝张开和闭合两种结构振动状态相符;隐状态平滑概率大部分在0 和100%两个值之间变化,满足裂缝损伤特有的变化模式。

图3 悬臂梁平滑概率时程Fig. 3 Time histories of smooth probability for cantilever beam
为计算方便,这里选择平滑概率由0 突变到100%作为裂缝的损伤模式,通过统计其出现次数N0→1判断损伤类型是否属于裂缝。N0→1值越大表明出现裂缝损伤的可能性也越大,比如范德波尔系统(图2)和3 自由度悬臂梁(图3)的N0→1值分别为1 和10。
3.3 损伤定位


图4 悬臂梁损伤定位结果Fig. 4 Damage location result for cantilever beam
3.4 损伤定量
裂缝损伤的严重程度一般用裂缝宽度表示。由式(15)可知,裂缝宽度可用裂缝开合瞬间(设为ts)损伤单元处的层间位移 |x2(ts)-x3(ts)|表示。根据3.2 节结论,这里的裂缝开合瞬间可代替为裂缝损伤模式出现的时间点tsi(i=1,2,···,N0→1)。因此,假设裂缝位于自由度i和j之间,其宽度Wc可表示为:

图5 给出3.2 节3 自由度系统的损伤定量结果。从图5 可以看出,由于存在样本不确定性,大部分裂缝宽度的估计值与真实值1 mm 偏差较大;按照式(17)对样本取平均可消除样本偏差,得到较为准确的裂缝宽度估值。

图5 悬臂梁损伤定量结果Fig. 5 Quantitative results of crack damage for cantilever beam
3.5 损伤识别流程
根据上述分析,基于MSVAR 模型的非线性损伤识别方法可分为两部分:第一部分是对结构响应建立MSVAR 模型,通过隐状态平滑概率构造信息熵判断结构是否出现损伤;第二部分是根据MSVAR 模型能够准确描述结构出现裂缝后的振动状态,进一步对损伤类型、损伤位置和损伤程度进行识别。损伤识别流程如图6 所示,具体可分为以下5 个步骤:
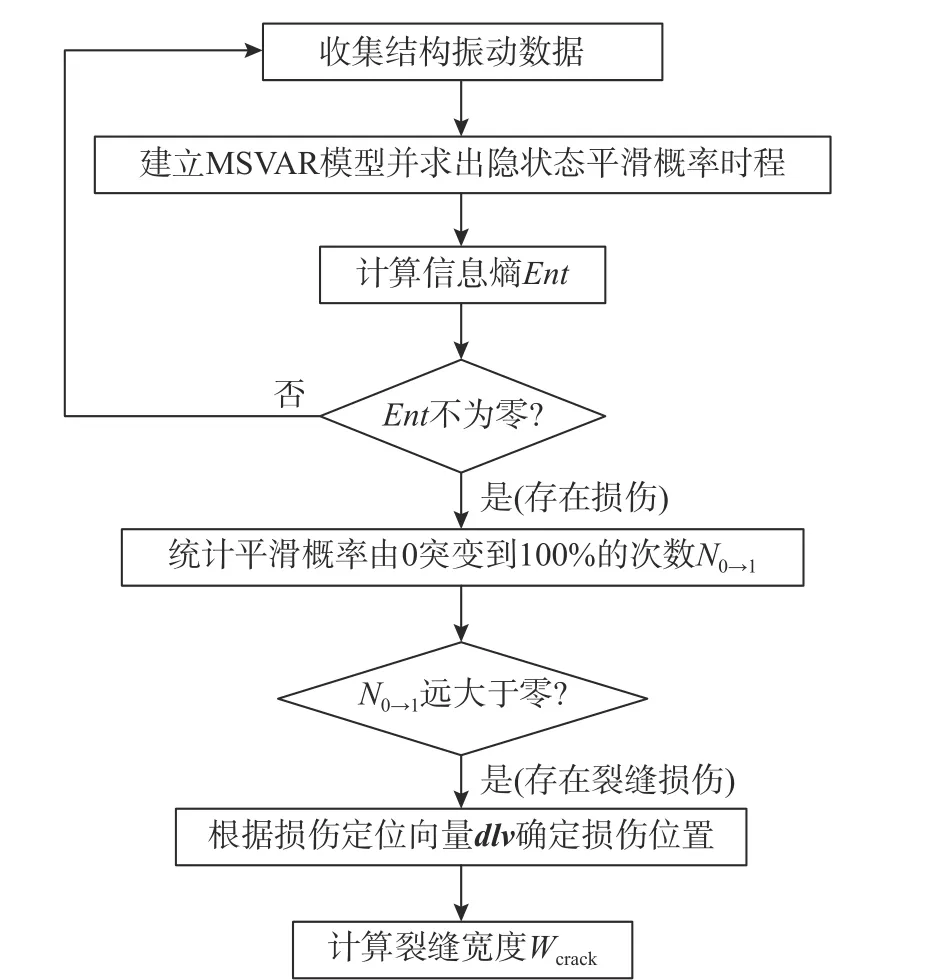
图6 非线性损伤识别流程Fig. 6 Nonlinear damage identification flowchart
步骤1:建立MSVAR 模型。收集结构振动数据并采用拟牛顿算法[29]估计MSVAR 模型参数。建模时需要根据均方根误差准则(RMSE)选择合适的VAR 模型阶数[23],然后采用贝叶斯信息准则(BIC)确定隐状态个数[21]。
步骤2:非线性损伤预警。计算式(8)隐状态平滑概率时程,之后根据式(11)求出信息熵Ent作为损伤预警指标。如果Ent大于零,则认为结构存在损伤。
步骤3:损伤类型识别。统计隐状态平滑概率从0 突变到100%的次数N0→1判断出现的损伤是否属于裂缝。N0→1值越大说明裂缝损伤的可能性越大。
步骤4:裂缝类型损伤定位。根据式(16)计算损伤定位向量dlv,以dlv最大值元素对应的自由度作为裂缝位置。
步骤5:估计裂缝宽度。根据步骤3 得到的N0→1个平滑概率突变时刻点以及步骤4 的定位结果,按照式(17)估计裂缝宽度。
4 试验验证
以美国洛斯阿拉莫斯实验室三层框架结构的试验数据[30]验证本文所提方法的有效性。如图7所示,该结构由铝板( 3 0.5 cm×30.5 cm×2.5 cm)和铝柱( 1 7.7 cm×2.5 cm×0.6 cm)通过螺栓连接而成。在结构第三层固定有悬臂柱和阻尼器,通过调节二者之间的缝隙宽度模拟裂缝损伤大小。受单向轨道约束,结构只能沿激励方向振动,白噪声激励的带宽为20 Hz~150 Hz。加速度传感器安装在每层铝板中间,采样频率为320 Hz。

图7 实验室三层框架结构[30]Fig. 7 Laboratory three-layer frame structure
试验总共设有17 个工况,如表1 所示。每个工况收集10 个加速度数据样本,每个样本均有320 个数据。为模拟环境噪声影响,采集的加速度数据混有高斯白噪声,数据信噪比为20 dB。

表1 三层框架结构的损伤工况[30]Table 1 Damage cases of three-layer frame structure
4.1 非线性损伤预警
对采集的加速度数据建立MSVAR 模型需要确定VAR 模型阶数和隐状态个数。首先采用RMSE准则选择合适的VAR 模型阶数。图8(a)给出4 个典型工况的RMSE 值随VAR 模型阶数变化的曲线,根据曲线拐点可判断VAR 模型阶数应取为2。确定VAR 模型阶数之后,需要根据BIC 准则选择隐状态个数。如图8(b)所示,工况14 的BIC值在隐状态个数为3 时达到最小,而其他工况的最佳隐状态个数为2。为避免欠拟合现象,这里选择MS(3)VAR(2)模型对结构加速度响应数据进行拟合。

图8 MSVAR 模型阶数确定结果Fig. 8 MSVAR model order determination results
图9 对比了基于MS(3)VAR(2)模型和基于MS(2)VAR(2)模型的损伤预警结果。由于数据噪声和建模误差等因素的影响,无损伤样本的信息熵一般不为零,需要根据参考工况(工况1)的信息熵设置损伤阈值,信息熵小于损伤阈值说明结构没有损伤。从图9 可以看出,两种MSVAR 模型均能准确预警损伤工况11~工况14 和工况17;但损伤工况10、工况15 和工况16 都被误认为健康工况,其原因是过大的缝隙宽度使得结构振动时阻尼器与悬臂柱几乎不发生碰撞,导致计算的信息熵很难与无损伤样本区分开。
隐状态个数过少的缺点主要体现在工况14 的信息熵整体偏小(图9(b)蓝色椭圆位置),甚至有个别样本的信息熵因小于损伤阈值而被误认为无损伤样本。考虑到工况14 属于小损伤工况(缝隙宽度只有0.05 mm),隐状态个数取值过小可能会降低本文所提方法对损伤的灵敏度。

图9 三层框架结构损伤预警结果Fig. 9 Damage warning results for frame structure
4.2 裂缝类型损伤识别
确定结构存在损伤后,需要根据MSVAR 模型平滑概率是否具有从0 突变到100%的变化模式进一步判断出现的损伤是否属于裂缝类型损伤。
以工况11~工况14 为例,这些损伤工况对应的MSVAR 模型隐状态平滑概率时程曲线如图10所示。从图10 可以看出,4 个损伤工况的MSVAR模型都有2 个隐状态被激活,而且隐状态之间的变化模式与裂缝损伤相同,存在平滑概率从0 突变到100%的特殊损伤模式。出现这种现象的原因是悬臂柱与阻尼器的碰撞使得结构第三层刚度出现双线性特征,继而导致结构在两种振动状态来回切换。


图10 不同损伤工况平滑概率曲线的对比结果Fig. 10 Comparisons of smooth probability curves under different damage cases
考虑建模误差和噪声干扰,裂缝的损伤模式放宽为隐状态平滑概率由小于5%突变到大于95%,其发生次数(仍记为N0→1)的统计结果如图11所示。因为工况11~工况14 的缝隙宽度由宽变窄,而减少缝隙宽度意味着结构振动时阻尼器与悬臂柱的碰撞机会增多(从图10 中也能看出隐状态1 和隐状态2 之间的切换频次与缝隙宽度成反比),所以工况14 的N0→1值最大,最有可能是裂缝类型损伤。需要特别指出的是,工况14 虽然属于小损伤工况,但其信息熵(图9(a))和N0→1值(图11)都远大于其他损伤工况,说明本文所提方法对早期裂缝较为敏感。
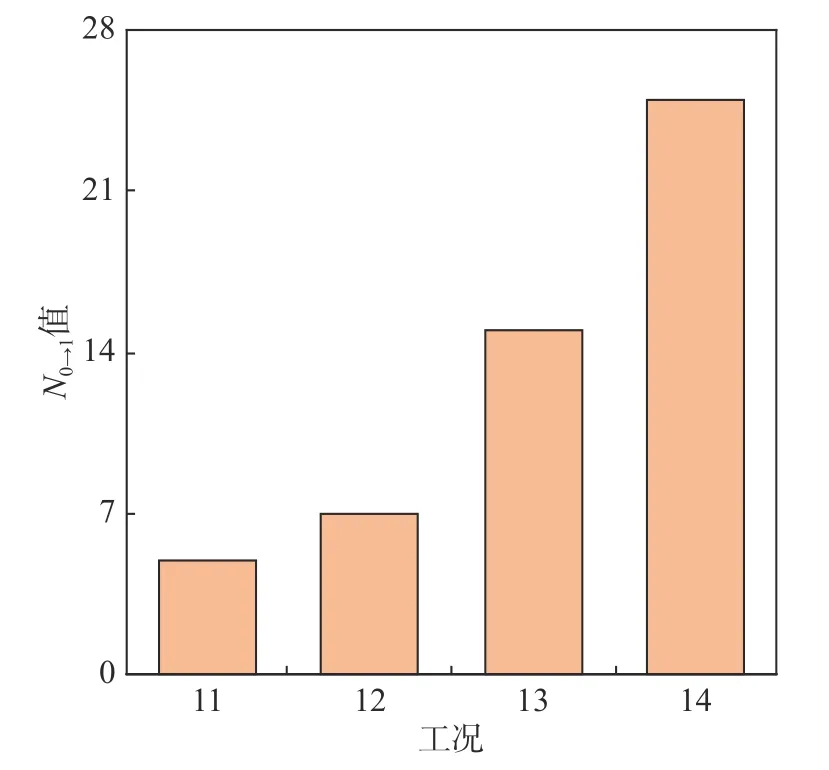
图11 裂缝损伤的隐状态转移模式出现次数统计Fig. 11 Statistical results of occurrence number for crack damage hidden state transition mode
4.3 损伤定位和定量
仍以工况11~工况14 为例,按照式(16)计算得到各工况的损伤定位向量如表2 所示。dlv3值最大表明裂缝位于传感器3,与实际裂缝位置相符。

表2 损伤定位结果Table 2 Damage location results
对采集的结构加速度响应数据进行二次积分和高通滤波得到结构位移响应数据,然后利用式(17)估计裂缝宽度。如表3 所示,损伤工况11~工况13 裂缝宽度的估计误差均控制在5%左右;工况14 裂缝宽度的估计偏差较大,其原因可能是加速度积分求得的位移与结构真实位移存在的误差与裂缝宽度相当。

表3 裂缝宽度估计结果Table 3 Crack width estimation results
5 结论
本文假定损伤会导致结构响应出现非线性特征,提出基于MSVAR 模型的非线性损伤识别方法。通过数值算例和模型试验得出以下结论:
(1)利用MSVAR 模型的隐状态平滑概率构造信息熵能够准确预警非线性损伤;
(2) MSVAR 模型第一阶自回归系数矩阵的对角线元素包含裂缝位置信息;
(3)确定裂缝位置后,采用平滑概率从0 突变到100%时刻的层间位移可近似裂缝宽度;
(4)本文所提方法对宽度较小的裂缝较为敏感,但隐状态个数取值过小会降低损伤预警精度。
需要指出的是,由于时域的时间序列模型通常易受噪声影响,将基于MSVAR 模型的损伤识别方法应用到实际工程需要解决环境噪声的干扰问题。另外,本文只针对裂缝类型损伤进行研究,后续需要验证所提方法在其他类型损伤(比如钢筋塑性变形等)的适用性。
