表面粗糙度对近壁圆柱体涡激振动响应影响的数值研究

熊友明，张壮壮，高 云，彭 庚，刘黎明，杨 斌

(1.西南石油大学 油气藏地质及开发工程国家重点实验室，成都 610500；2.哈尔滨工业大学(威海) 海洋工程学院，山东 威海 264209；3.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；4.中国石油西南油气田工程技术研究院，成都 610031)

海底管道是海洋油气开采运输过程中必不可少的设备。海底地势由于高低不平的特性，外加海流对海底的冲刷作用，会导致直接铺设在海底的管道出现悬挂段。管道悬挂段长度有时可达到100倍管道直径，悬跨段与海底之间的最大间距可达到2倍～3倍管道直径[1]。当管道悬挂段承受一定流速的来流时，会在管道周围形成交替脱落的漩涡，周期性的漩涡脱落会在结构上产生周期性的载荷，进一步导致结构发生振动，称为涡激振动[2]。涡激振动是导致海底管道产生疲劳破坏的重要因素，因此必须对该问题给予高度重视，海底管道悬挂段的涡激振动响应问题可以简化为一受弹性支撑的双自由度近壁圆柱体涡激振动响应问题。

过去针对处于无限流场中不考虑壁面效应的圆柱体涡激振动响应问题的研究较多。通过这些研究可以发现涡激振动响应具有很多重要的机理特性。当漩涡脱落频率(fv)与结构固有频率(fn)接近时，便会发生锁定(Lock-in)现象，锁定区间里，涡激振动响应幅值将明显增加[3]。Khalak等[4]通过研究发现涡激振动响应幅值依据质量阻尼比(m*ζ)可分为两种类型：①对于低质量阻尼比圆柱体，基于涡激振动响应幅值变化趋势可将折合速度区间大致划分为初始分支、上分支以及低分支三个区间；②对于高质量阻尼比圆柱体，上分支区间消失，只剩下初始分支和低分支两个区间。且不同的分支对应不同的尾部漩涡发放模式：对于初始分支，圆柱体尾部流场在一个周期内发放两个单一漩涡，该模式称为2S模式；而对于上分支以及低分支，尾部流场在一个周期内则发放两对漩涡，该模式称为2P模式。

当圆柱体位于壁面附近时，壁面的存在会导致结构尾部流场特性更为复杂。对于近壁圆柱体，除了在结构上边缘以及下边缘形成两个剪切层外，还会在固定壁面上形成一个剪切层。针对近壁圆柱体的涡激振动响应研究可包括：完全固定的近壁圆柱体研究[5-10]以及具有弹性支撑可振动的近壁圆柱体研究[11-17]。固定的近壁圆柱体研究主要针对尾部流体激励特性(漩涡发放频率、漩涡发放模式、拖曳力、升力等)进行研究；而振动的近壁圆柱体研究除了流体激励特性研究外，还包括结构振动响应特性(振动幅值、振动频率以及锁定区间等)研究。实际上，在涡激振动响应过程中，漩涡脱落作为流体激励引发结构发生振动，结构振动又会反过来改变尾部流场的漩涡脱落从而影响流体激励。因此，涡激振动是一典型非线性流固耦合问题，受周围流场特性影响显著，而雷诺数和表面粗糙度则正是影响结构尾部流场特性的两个重要参数。海底管道悬跨段在使用过程由于海洋生物体的附着影响到结构的表面粗糙度，会进一步对尾部流场激励特性以及结构振动响应特性带来影响。关于表面粗糙度如何影响近壁圆柱体的尾部流场特性从而进一步影响结构振动响应特性，这部分研究还有待深入展开。

基于此，本文在第3部分对表面粗糙度对近壁圆柱体的涡激振动响应特性影响展开了系统地研究：在3.1部分，对数值计算时采用的网格进行了独立性研究并对数值模型可靠性进行了验证；在3.2部分，基于表面粗糙度对圆柱体的振动幅值、振动频率以及锁定区间的影响进行了研究；在3.3部分，基于表面粗糙度对圆柱体流体力系数以及斯脱哈尔数的影响进行了研究。在3.4部分，基于表面粗糙度对圆柱体振动轨迹特性的影响进行了研究。

1 问题描述

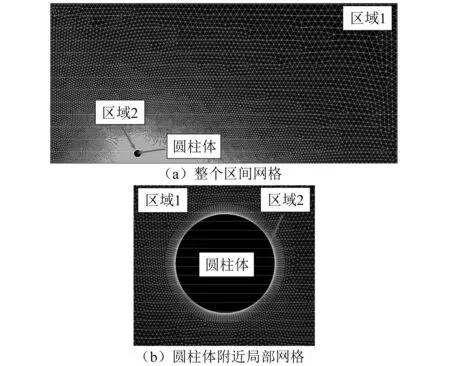
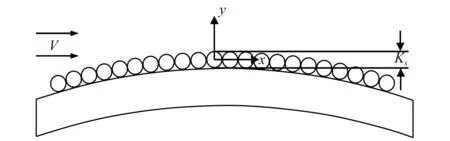
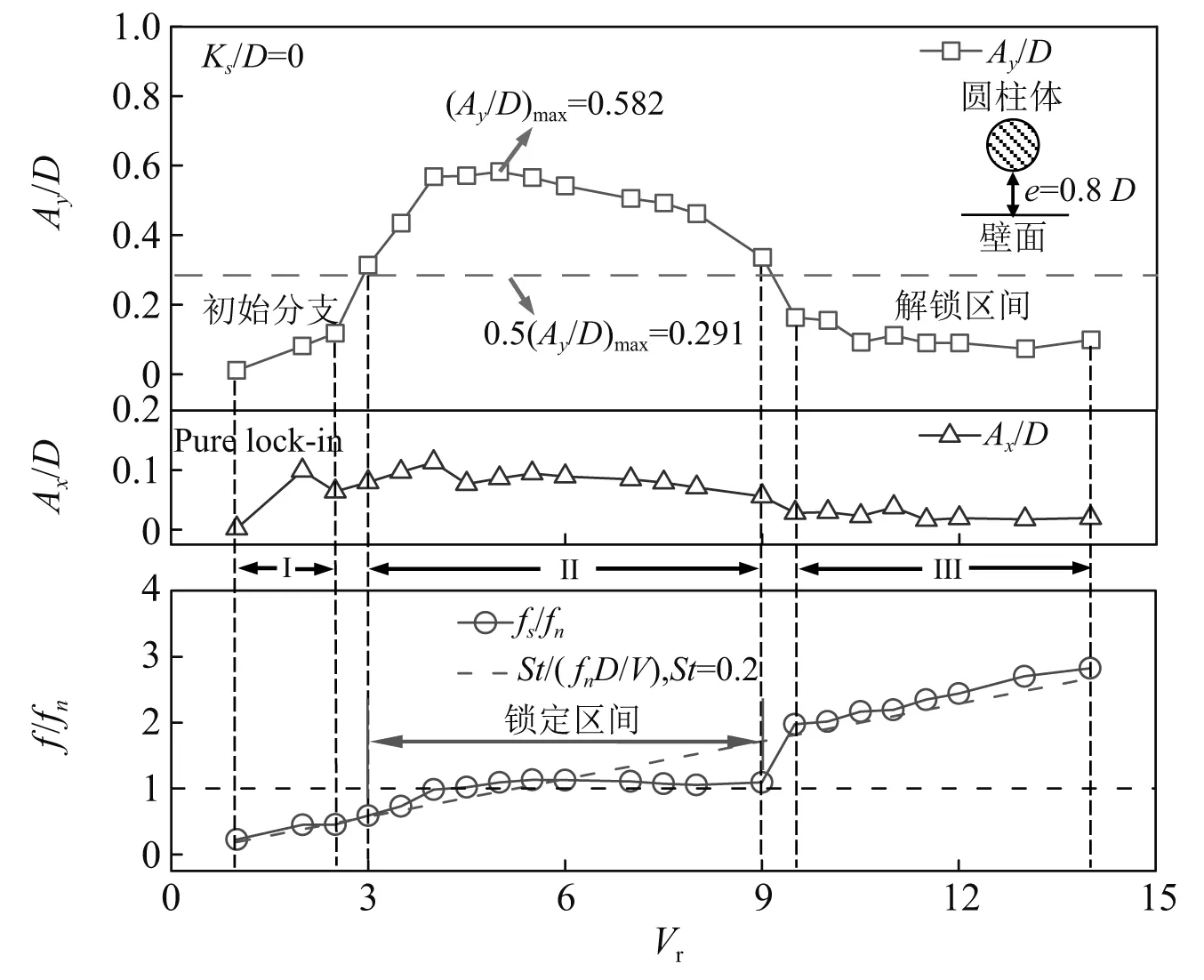
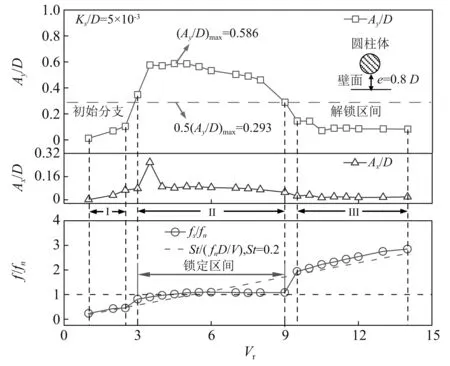
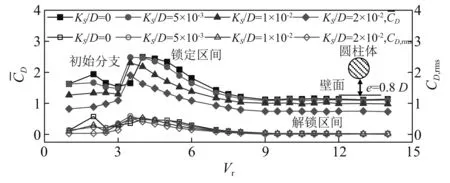
图1给出了本文数值研究的计算区域以及边界条件。一直径为D的圆柱体放置在流速为V的均匀流场中，圆柱体直径D取为0.2 m。计算区域流场总长度取为48D，圆柱体中心距离入口边界和出口边界分别为12D和36D。流场总宽度取为22D，因此阻塞率为0.045，当阻塞率低于0.05时，流场宽度对结构响应影响可忽略[18-19]。这里阻塞率选为0.045可保证在可行的计算时间内做出精细的数值研究。图1中，u和v分别表示流速在水平方向和垂直方向上的分量。流场入口边界条件取为：u=V以及v=0；出口边界条件取为：∂u/∂x=0以及∂v/∂x=0；上边界取为∂u/∂y=0以及v=0；下边界取为u=0以及v=0；圆柱体表面取为无滑移边界条件：u(t)=dx(t)/dt以及v(t)=dy(t)/dt。如图1所示，假设初始时刻圆柱体下边界与壁面之间的间距为e。近壁圆柱体振动响应特性依据间距e大小可大致划分为三个区间[20]：①当e≥D时，此时圆柱体振动响应特性受壁面影响较小，圆柱体振动响应特性与不存在壁面的无限流场中结构振动响应特性非常接近；②当0.3D≤e

图1 计算区域以及边界条件Fig.1 Computational domain and boundary conditions

由图1虚线圆框所示的局部放大图可以看出：近壁圆柱体可以在x方向和y方向同时发生振动。雷诺数Re定义为[21]：Re=VD/v，其中v为流体的运动黏性系数。本文Re取5 000且保持不变，意味着流速V保持不变。折合速度Vr通常可定义为：Vr=V/(fn×D)，由于流速V和直径D均保持不变，因此只能通过改变固有频率fn去改变折合速度Vr。通过改变固有频率来改变折合速度的方法在过去得到了较为广泛的应用[22-26]。数值研究过程中总共考虑了4种不同表面粗糙度的圆柱体，粗糙度系数Ks/D分别取为0，5×10-3，1×10-2以及2×10-2。对于每种表面粗糙度，依次研究了分布在1～14之间的22种折合速度，因此总共研究了88种工况。研究过程中质量比m*以及阻尼比ζ分别取为2.6以及0.003 6且保持不变。

2 控制方程以及数值方法

2.1 控制方程

假设二维圆柱绕流问题可使用不可压缩非稳定雷诺平均Navier-Stokes(URANS)方程来加以描述，其质量守恒以及动量守恒方程可写作

(1)

(2)

其中

(3)

式(1)～式(3)中，xi和xj分别表示在i方向和j方向的坐标轴，这里x1表示x坐标轴，x2表示y坐标轴；因此，ui和uj分别表示在x方向和y方向的瞬时速度；u′i和u′j分别表示在x方向和y方向的脉动速度。t表示时间；p表示压力；ρ表示流体密度；vt表示湍流黏度；κ表示湍流动能。δij为克罗内克函数，可表示为

(4)

式(1)～式(3)中，参数上面加一横线表示对参数求时间平均值。如图1所示，将振动系统看作是一双自由度质量-弹簧-阻尼系统，系统在顺流方向(x方向)以及横流方向(y方向)的振动方程可写作

(5)

式中：x(t)，dx(t)/dt以及d2x(t)/dt2分别表示结构在x方向的振动位移、振动速度以及振动加速度；y(t)，dy(t)/dt以及d2y(t)/dt2分别表示结构在y方向的振动位移、振动速度以及振动加速度；FD(t)和FL(t)分别表示单位长度圆柱体上受到的拖曳力和升力；m为单位长度圆柱体质量，包括结构质量以及流体附加质量，可表示为m=ms+mA=(m*+CA)md，其中CA为附加质量系数，md为结构排开液体的质量，md=ρπD2/4，ρ为液体密度。ω0和ζ分别表示系统的固有圆频率以及结构阻尼比，表示如下

(6)

式中：c和k分别表示系统单位长度上的阻尼系数和刚度系数。本文数值研究中c，k，m*以及CA均来自于Jauvtis和Williamson的实验数据[27]，圆柱体初始条件取为在x方向以及y方向的位移和速度均为0，如下

(7)

2.2 数值方法

这里以横流方向(y方向)圆柱体振动为例进行数值求解方法介绍，将式(5)第二项重写成

(8)

基于经典四阶龙格库塔法，将式(8)离散为

(9)

其中

(10)

式中：K1，K2，K3，K4，L1，L2，L3以及L4分别表示四阶龙格库塔法转换因子；Δt为时间步长；若确定了tn时刻结构的振动位移y(tn)和振动速度v(tn)，则可基于式(8)～式(10)求解得到tn+1时刻(tn+1=tn+Δt)的振动位移y(tn+1)以及振动速度v(tn+1)。

本文数值研究过程中采用了动网格技术，如图2所示，将计算区域划分为两大块：区域1和区域2。区域1为变形区域，采用三角形网格进行划分；区域2为包围圆柱体的随动区域，采用四边形网格进行划分。区域2里的网格随着圆柱体运动进行同步运动，而区域1里的网格则随着圆柱体的运动进行实时更新。圆柱体的振动位移通过用户自定义函数(user defined function,UDF)进行实时计算并进行更新。数值研究中所有的方程均基于商业软件FLUENT进行求解。在进行圆柱体表面粗糙度模拟时，本文使用等效沙粒粗糙度模型对其加以数值模拟，该方法在过去实验以及数值研究中均得到了较为广泛的应用[28-29]。如图3所示，假设Ks为附着在圆柱体表面的沙粒直径，则可将沙粒直径与圆柱直径的比值Ks/D定义为表面粗糙度系数。

图2 计算网格Fig.2 Computational mesh

图3 等效沙粒粗糙度数值模拟Fig.3 Numerical simulation of equivalent sand surface roughness

3 分析与讨论

3.1 网格独立性研究以及数值模型验证

在正式进行分析之前，需要对本文数值研究中所采用的网格进行独立性研究。网格独立性研究基于光滑圆柱体展开，仅对Vr=6.0进行了研究。网格独立性研究时选取了4种不同密度的网格，表1给出了使用每个网格计算得到的Ax/D，Ay/D以及fs/fn，fs为结构在横流方向振动响应的主导频率；fn为结构固有频率，与2.1部分固有圆频率ω0之间的关系为：fn=ω0/2π。Ax/D和Ay/D分别表示结构在顺流方向以及横流方向的无量纲振幅比，表示如下

表1 网格独立性研究Tab.1 Mesh independency study

Ay/D=|Ymax-Ymin|/2D,Ax/D=|Xmax-Xmin|/2D

(11)

式中：Ymax与Ymin表示结构横向振动位移最大值和最小值；Xmax以及Xmin表示结构流向振动位移最大值以及最小值。

由表1可以看出：当网格密度从M1变化到M2时，Ax/D，Ay/D以及fs/fn的变化率依次为4.33%、3.47%以及2.66%；当网格密度从M2变化到M3时，Ax/D，Ay/D以及fs/fn的变化率依次为2.64%、2.13%以及1.34%，当网格密度从M3变化到M4时，Ax/D，Ay/D以及fs/fn的变化率依次为0.74%、0.59%以及0.38%。随着网格密度的逐渐加大，计算得到的Ax/D，Ay/D以及fs/fn的变化率依次为0.74%、0.59%以及0.38%。随着网格密度的逐渐加大，计算得到的Ax/D，Ay/D以及fs/fn变化率均呈下降趋势。使用密度为M3网格计算得到的结果与M4网格计算得到的结果已非常接近，最大误差控制在1%以内。在Intel®CoreTMi5-4590平台上，使用M3网格完成计算所需时间为11 h，而使用M4网格完成计算所需时间为14 h。因此，在满足一定计算精度的条件下，综合考虑计算成本的因素，本文数值计算过程中采用M3网格。

这里紧接着对本文数值模型的可靠性进行了验证，数值验证过程中质量比、阻尼比以及间隙比的选取来源于Li等[30]的研究(m*=10,ζ=0以及e=0.9D)。图4给出了本文Ax/D，Ay/D以及fs/fn的数值结算结果与Li等研究结果的对比。图4可看出：涡激振动响应具备明显的锁定区间，当折合速度进入锁定区间时，振幅会大幅增加；当折合速度离开锁定区间时，振幅会迅速下降。总体来说：本文的数值模拟结果与他人分析结果吻合良好，从而验证了本文数值方法的可靠性。

图4 本文数值模拟结果与文献[30]结果对比Fig.4 Comparison of present numerical results and other reference’s results [30]

在以下分析部分中(3.2～3.4节)，将使用该方法研究具有不同参数的近壁圆柱的VIV问题。本验证部分(第3.1节)中的主要无量纲参数与以下分析部分(3.2～3.4节)中相应参数之间的差异列于表2。值得注意的是，分析部分中使用的数值方法与本验证部分中使用的方法相同，因此没有进行额外的验证。

表2 主要无量纲参数Tab.2 Main dimensionless parameters

3.2 响应幅值以及响应频率分析

图5到图8分别给出了光滑圆柱体以及带有三种不同粗糙度(Ks/D=5×10-3，Ks/D=1×10-2以及Ks/D=2×10-2)圆柱体在横向和流向振动幅值、横向振动频率以及锁定区间。横向振动频率可由横向振动位移时间历程曲线做快速傅里叶变换(fast fourier transform,FFT)再取主导频率得到。锁定区间判定方法参考文献[31]，即当振幅大于整个折合速度区间里最大振幅的一半时，认为发生锁定。

如表3所示，依据横向振幅变化趋势，可以将整个折合速度区间大致划分为：初始分支(initial branch)、锁定区间(lock-in region)以及解锁区间(desynchronization region)三部分。由图可以看出：对于初始间距为0.8D的近壁圆柱体，当Ks/D=0、Ks/D=5×10-3，Ks/D=1×10-2以及Ks/D=2×10-2时，横向无量纲振幅比最大值依次为0.582，0.586，0.634以及0.660；随着圆柱体表面粗糙度的增加，结构横向振幅最大值呈上升趋势。

表3 折合速度划分区间Tab.3 Reduced velocity ranges for the flow regimes

由图5可以看出：对于光滑圆柱体，在初始分支区间里(1≤Vr≤2.5)，横向振幅随着Vr的增加缓慢增加；且流向振幅与横向振幅大小相当，这是由当折合速度较小时流向会产生Pure-lock-in所导致[32]；初始分支里结构振动频率与斯脱哈尔漩涡发放频率[33]吻合良好。随着Vr的增加(Vr≥3)，结构振动进入锁定区间，在锁定区间里，随着Vr的增加，横向振幅呈“先快速增加、再缓慢增加、最后缓慢下降”的趋势，锁定区间为3～9；锁定区间里，与横向振幅相比，流向振幅很小；且锁定区间里结构振动频率将脱离斯脱哈尔漩涡发放频率，而偏移到结构固有频率附近。随着Vr的进一步增加(Vr≥9.5)，结构振动将离开锁定区间，进入解锁区间，横向振幅先快速下降到0.15D附近，随后稳定在0.1D附近；当Vr进入解锁区间里，结构振动频率将出现跳跃现象：从固有频率附近再次跳跃到斯脱哈尔漩涡发放频率。

图5 光滑圆柱体无量纲振幅比、结构振动频率以及锁定区间Fig.5 Non-dimensional displacements,structural vibration frequencies and lock-in region for a smooth cylinder

将图6～图8的粗糙圆柱体涡激振动响应特性与图5的光滑圆柱体涡激振动响应特性加以对比，可以发现：对于粗糙度较小(Ks/D=5×10-3)和中等(Ks/D=1×10-2)的粗糙圆柱体，与光滑圆柱体相比，锁定区间没有发生变化，折合速度区间仍然为3～9；但对于粗糙度较大(Ks/D=2×10-2)的粗糙圆柱体，与光滑圆柱体相比，锁定区间宽度变窄为3.5～8。随着表面粗糙度的上升，初始分支区间的Pure-lock-in现象变得越来越不明显，当圆柱体表面粗糙度增加到2×10-2时，Pure-lock-in现象完全消失；且随着粗糙度的上升，“由初始分支进入锁定区间时出现的振幅突增特性”以及“由锁定区间进入解锁区间时出现的振幅突降特性”越来越明显。

图6 Ks/D=5×10-3粗糙圆柱体无量纲振幅比、结构振动频率以及锁定区间Fig.6 Non-dimensional displacements,structural vibration frequencies and lock-in region for a rough cylinder with Ks/D=5×10-3

图7 Ks/D=1×10-2粗糙圆柱体无量纲振幅比、结构振动频率以及锁定区间Fig.7 Non-dimensional displacements,structural vibration frequencies and lock-in region for a rough cylinder with Ks/D=1×10-2

图8 Ks/D=2×10-2粗糙圆柱体无量纲振幅比、结构振动频率以及锁定区间Fig.8 Non-dimensional displacements,structural vibration frequencies and lock-in region for a rough cylinder with Ks/D=2×10-2

3.3 流体力系数和斯脱哈尔数分析

流体力系数包括升力系数和拖曳力系数，二系数可由第2部分计算得到的升力和拖曳力做无量纲处理得到，可表示为

(12)

在得到升力系数和拖曳力系数后，取流体力系数稳定段区间里n个数据样本点，基于这些样本点得到升力系数均值、拖曳力系数均值、升力系数均方根值以及拖曳力系数均方根值，表示如下

(13)

图9给出了不同粗糙度下圆柱体的升力系数均值以及升力系数均方根值。结合图9以及表3可以看出：随着折合速度的增加，升力系数均方根值呈现先增加后减小的趋势；结合第3.2节中的振动响应幅值分析结果发现：在整个Vr区间里，升力系数均方根值最大值对应的Vr并不与横向振幅最大值对应的Vr相对应，而是出现在初始分支与锁定区间交界处附近。对于近壁圆柱体，当Vr处于初始分支区间时，由于横向振幅较小，因此壁面效应不明显，导致升力系数均值在0附近；随着Vr的增加进入锁定区间时，此时横向振幅较大，壁面效应随之增加，使得漩涡发放上下不对称性更为明显，进一步导致升力系数均值明显大于0。当Vr进入解锁区间后，横向振幅再次变小，壁面效应随之减小，升力系数均值再次稳定在0附近。

图9 不同粗糙度圆柱体的升力系数均值以及升力系数均方根值Fig.9 Mean lift coefficient and root-mean-squared lift coefficient for cylinders with different surface roughnesses

图10给出了不同粗糙度下圆柱体的拖曳力系数均值以及拖曳力系数均方根值。由图10可以看出：在初始分支以及锁定区间里，随着Vr的增加，圆柱体的拖曳力系数均值呈现“先增加、后减小”的趋势。对于光滑圆柱体以及粗糙度最大(Ks/D=2×10-2)的粗糙圆柱体，当Vr=4以及Vr=3.5时，拖曳力系数均值依次出现最大值2.5和2。随着粗糙度的上升，拖曳力系数均值最大值呈下降趋势，且最大值对应的Vr逐渐减小。当Vr进入解锁区间后，拖曳力系数均值均趋于稳定：对于光滑圆柱体以及粗糙度最大(Ks/D=2×10-2)的粗糙圆柱体，拖曳力系数均值分别稳定在1.2以及0.8附近。随着折合速度增加，拖曳力系数均方根值变化趋势类似于拖曳力系数均值变化趋势。对于光滑圆柱体，拖曳力系数均方根值最大值出现在初始分支区间，这是由Pure-lock-in所导致；对于粗糙圆柱体，锁定区间的拖曳力系数均方根值很明显要大于另外两个区间。斯脱哈尔数即无量纲化以后的尾部流场漩涡发放频率，可表示如下

图10 不同粗糙度圆柱体的拖曳力系数均值以及拖曳力系数均方根值Fig.10 Mean drag coefficient and root-mean-squared drag coefficient for cylinders with different surface roughnesses

(14)

对于稳态流中的圆柱体尾部流场，漩涡发放频率和升力频率相同，可通过对升力时间历程曲线求FFT变换后再取主导频率得到，式(14)中fv即为升力主导频率。

图11给出了不同粗糙度圆柱体的斯脱哈尔数。由图11可以看出：在初始分支区间里，随着Vr的增加，斯脱哈尔数呈现“先减小、后增加”的趋势；当Vr进入锁定区间后，斯脱哈尔数随着Vr的增加基本呈下降趋势。对于光滑圆柱体、表面粗糙度较小(Ks/D=5×10-3)的粗糙圆柱体、表面粗糙度中等(Ks/D=1×10-2)的粗糙圆柱体以及表面粗糙度较大(Ks/D=2×10-2)的粗糙圆柱体，当Vr=9，Vr=8，Vr=8以及Vr=6时，斯脱哈尔数依次出现最小值0.12，0.13，0.13以及0.17。随着表面粗糙度的上升，斯脱哈尔数最小值呈上升趋势，且最小值出现的Vr逐渐提前。当Vr离开锁定区间进入解锁区间后，斯脱哈尔数呈现明显的跳跃增加特性，随后在解锁区间里，随着Vr的增加，斯脱哈尔数呈稳定趋势。

图11 不同粗糙度圆柱体的斯脱哈尔数Fig.11 Strouhal number for cylinders with different surface roughnesses

3.4 振动轨迹分析

图12给出了不同粗糙度下圆柱体的振动轨迹，由图可以看出不同表面粗糙度下圆柱体振动轨迹特性非常相似，但当Vr处在不同折合速度区间，结构振动轨迹呈现明显不同的特性。当Vr=2处于初始分支区间时，圆柱体振动轨迹呈“斜八字”形；当Vr=8处于锁定区间时，结构振动轨迹呈现“斜椭圆”形；而当Vr=5处于Vr=2以及Vr=8之间时，结构振动轨迹则呈现“斜八字”形和“斜椭圆”形的双重特性。当Vr=12处于解锁区间时，结构振动轨迹呈“斜D字”形。对于整个区间里的所有折合速度，振动轨迹均呈现出上下不对称特性，这是由壁面效应所产生。

图12 不同粗糙度圆柱体的振动轨迹Fig.12 Vibration trajectories for cylinders with different surface roughnesses

4 结 论

本文针对粗糙度对近壁圆柱体涡激振动响应特性的影响进行了数值研究。圆柱体质量比、阻尼比、雷诺数以及初始间距比依次取为2.6，0.003 6，5 000以及0.8。对光滑圆柱体以及3种具有不同粗糙度的粗糙圆柱体涡激振动响应特性进行了分析，分析参数包括：结构振动幅值、结构振动频率、锁定区间、流体力系数以及斯脱哈尔数等。通过以上分析，可得到如下结论：

(1)依据近壁圆柱体的结构振动幅值以及结构振动频率，可以将整个折合速度区间大致划分为：初始分支、锁定区间以及解锁区间三部分；随着表面粗糙度的增加，结构横向振幅最大值呈上升趋势，而锁定区间宽度则呈减小趋势。

(2)对于近壁光滑圆柱体，在初始分支区间里，流向振动幅值出现非常明显的Pure-lock-in现象，但随着表面粗糙度的上升，初始分支区间里的Pure-lock-in现象逐渐消失，但初始分支进入锁定区间时的振幅突增特性以及锁定区间进入解锁区间时的振幅突降特性则越来越明显。

(3)对于近壁圆柱体，当折合速度位于锁定区间时，较大的结构横向振幅会导致壁面效应明显增加，进一步使得升力系数均值明显大于0；随着表面粗糙度的上升，拖曳力系数均值最大值呈下降趋势，且最大值对应的折合速度逐渐减小。

(4)对于近壁圆柱体，折合速度离开锁定区间进入解锁区间时，斯脱哈尔数呈现明显的跳跃增加特性；随着表面粗糙度的增加，发生跳跃点所对应的折合速度逐渐减小。随后在解锁区间，斯脱哈尔数逐渐保持稳定，且表面粗糙度越大，稳定时的斯脱哈尔数也越大。

(5)对于近壁圆柱体，不同表面粗糙度下圆柱体振动轨迹特性非常相似，但在不同折合速度区间，由于壁面效应的影响会导致结构振动轨迹呈现明显不同的特性。