一道竞赛题的探究

重庆三峡学院数学与统计学院 (404000) 罗 建 古玲玲 陈晓春

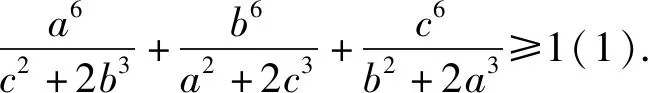
本文拟对不等式(1)的证明方法、变式、推广等方面作一探究．

1．不等式(1)的证法探究

分析1:不等式(1)的左端结构对称，利用柯西不等式有：

分析2：若注意到不等式(1)的左端的结构，利用基本不等式证明局部不等式后再叠加则有：

分析3：前述两种证法的关键是寻求a2+b2+c2与a3+b3+c3的不等关系，除证明1及证明2 外，还有

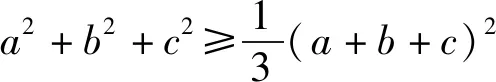
2．不等式(1)的变式

从证明1的过程可知，在使用柯西不等式后只要分母的和a2+b2+c2+2(a3+b3+c3)以及分子的和a3+b3+c3不变，其证明方法都是相同的，因此可得如下(1)的变式不等式：

2.1 将分子的元素轮换

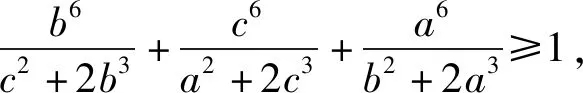
2.2 将分母的元素重排

2.3 将分母的元素拆分并轮换

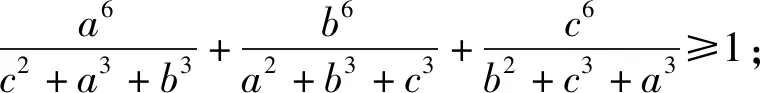
2.4 将分母的多项式扩充

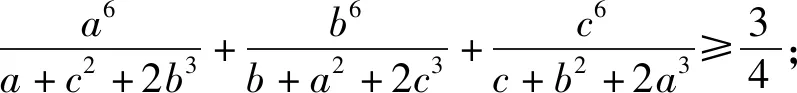
显然，通过对不等式中相应项的变式有很多，因此不等式(1)的变式还有许多，有兴趣的不妨一试．

3．不等式(1)的推广

推广是数学探究中的一种常用的思维形式，将不等式(1)的系数一般化，元素个数推广有：

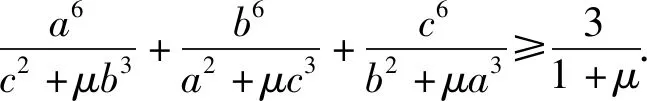
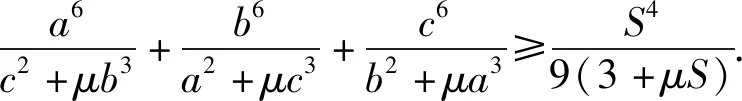
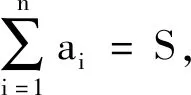
不等式5-8，前一个均是后一个的特例，下面只给出不等式8的证明．