关注平面区域的其他解题功能
2021-11-10浙江省杭州市富阳区江南中学311421
浙江省杭州市富阳区江南中学 (311421) 余 涛
在一些题目中经常会出现关于两个变量的不等式(组),或者在推理化简过程中出现此类情形,那么此类问题解决的一个重要思路就是找出不等式(组)所对应的几何意义,即用平面区域分辨出变量在平面中的变化范围,从而抓住解题的契机,本文通过对几个典型问题的分析与探究,揭示平面区域的其他解题功能,供读者朋友参考.
1、求几何概率
在一些求概率问题中,常涉及两个变量在一定的约束条件下变化,必须用平面区域将问题几何化,利用平面几何知识帮助解题.
例1 已知关于x的一元二次方程x2+2ax+b2=0,若a是区间[0,3]内任取的一个实数,b是区间[0,2]内任取的一个实数,求上述方程有实根的概率.
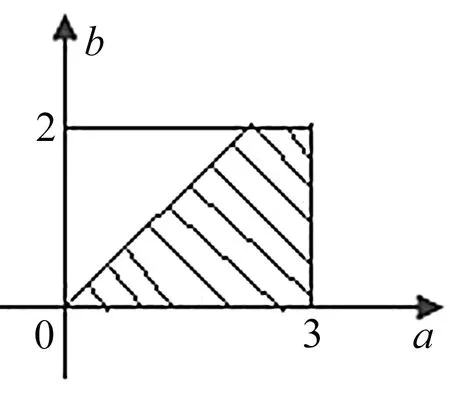
图1

评注:通过分析题目可知,本题是关于两个实数对的问题,而且这两个实数还有其他的约束条件,这就需要我们通过画出对应的构成区域,研究满足题意的各自的面积,然后由面积比解决问题.
2、求三角形中的范围
在一些关于三角形的问题中,因为三角形的三边之间存在约束条件,而有的题目本身也给出一些构成条件,这样通过转化就形成一些约束范围,利用这个范围就是解题中的重要步骤.

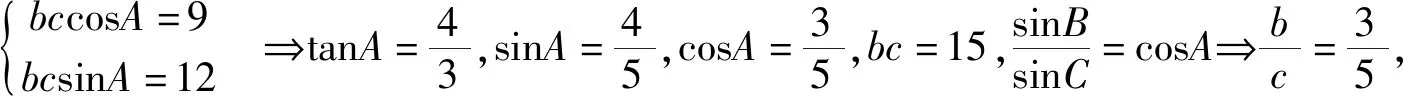

评注:本题虽然是一个解三角形的问题,但在解决后面的取值范围问题时必须由线性区域来帮助完成,体现了此知识点应用广泛性,同样,在很多范围问题中都隐藏着这一情况.
3、解决函数中的参数范围
在求函数的最大值或最小值问题中,如果已经给出了一些不等条件,在使用这些条件组时,应该考虑到用平面区域协助求出公共的范围,这样才能准确的确定相关参数的取值范围.
例3f(x)是定义在R上的增函数,且对任意的x都有f(1-x)+f(1+x)=0恒成立,如果实数m、n满足不等式f(m2-6m+23)+f(n2-8n)<0(m>3),求m2+n2的取值范围.
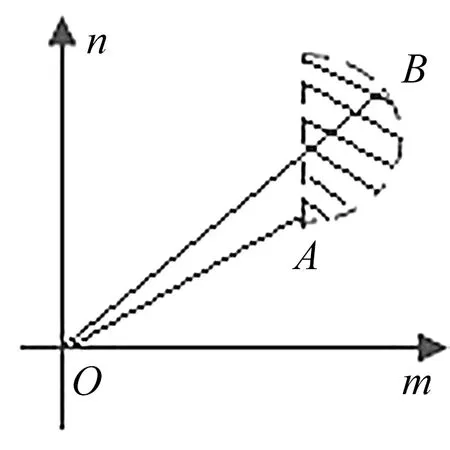
图2

评注:本题主要考查内容是函数性质的运用,当问题经过化简和推演后变成了一个含有两个变量的不等式,如何继续?就得需要画平面区域帮助解决.
4、确定大小关系
对于含有两个变量的不等式组中,不只是线性区域的内容,也有许多是非线性区域的,如关于圆锥曲线的,同样的方法,我们也是通过画出相关的平面区域协助解题.


图3

评注:用平面区域将给出的不等关系的几何意义表示出来后,所需比较两个实数的大小问题就是一个特殊情况下的结果,所以对获得的平面区域分析研判就是解题核心所在.
5、解决多元最值
一个表达式如果能取到最大值或最小值,都是在特定情形或特殊位置上取得的,如果给出条件是不等关系,那么这个特殊情况就是某个极限位置,用画平面区域的方法可以比较直观地找到极限位置.
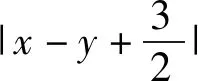
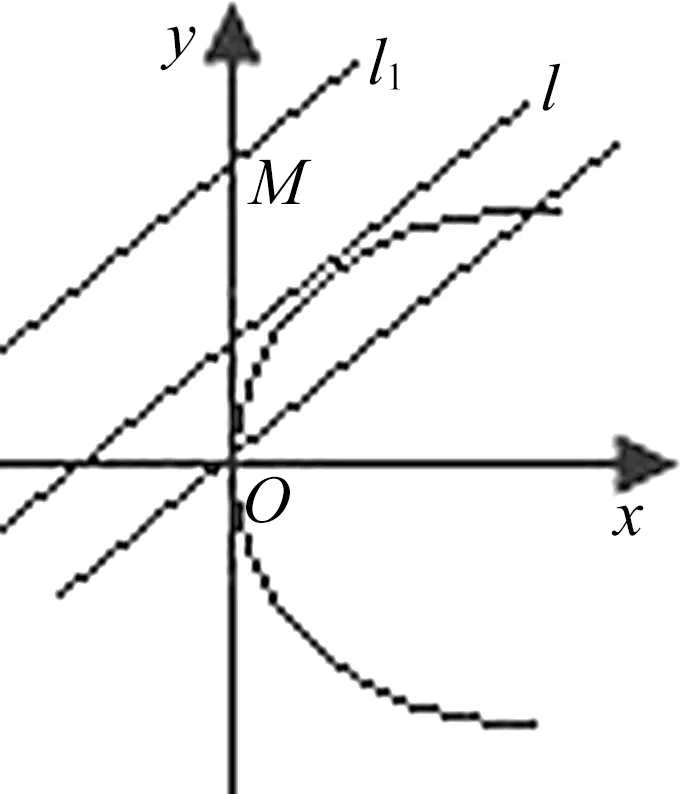
图4
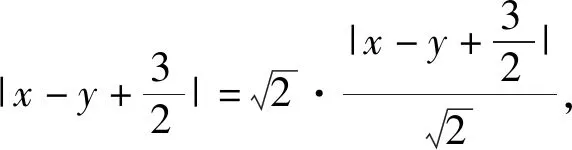
评注:首先将待求的绝对值变形转化为求动点到定直线的距离的最小值问题;而将给出的二元三次不等式分解成熟悉的二次不等式与一次不等式组,利用平面区域表示出它的几何意义,通过分析研判得到解题方案是成功解题的关键.
