走向深度融合：一道椭圆试题的探析与拓展

江苏省海门中学 (226100) 渠怀莲

(1)求椭圆C的方程；

(2)点M，N在C上，且AM⊥AN，AD⊥MN，D为垂足．证明：存在定点Q，使得DQ为定值．

分析：(1)由题意得到关于a,b,c的方程组，求解方程组即可确定椭圆方程.(2)设出点M，N的坐标，在斜率存在时设方程为y=kx+m，联立直线方程与椭圆方程，设而不求，根据已知条件，已得到m，k的关系，进而得直线MN恒过定点，在直线斜率不存在时要单独验证，然后结合直角三角形的性质即可确定满足题意的点Q的位置.

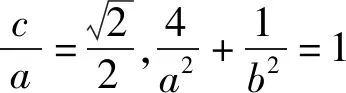
图1

图2

试题探析：如何探索问题的突破口，其核心是挖掘出直线MN经过定点.本题考查椭圆的标准方程和性质，圆锥曲线中与斜率之和、积有关的定点定值问题，关键是第二问中证明直线MN经过定点，并求得定点的坐标，属综合题，难度较大.根据已知条件，找到m，k的关系，事实上，这一步相当关键，也不容易化简到，主要是化简的方向要明确，采用了选主元的方法或双十字相乘法分解因式，选取k为主元，先对常数项中m十字相乘法，再对k十字相乘法因式分解4k2+8mk+(3m2-2m-1)=0，即得(2k+3m+1)(2k+m-1)=0.

1.如何想到直线MN恒过定点

解决问题的切入点是抓住直线MN经过定点这一特征，我们是如何关注到这一特征呢？事实上，问题的设问在暗示我们朝着这一方向处理，因为我们需要寻求一定点Q，使得DQ为定值，若存在，根据圆的定义，我们可知动点D的轨迹是圆，想到阿波罗尼斯圆、圆的直径式方程等都需要两个定点，而一方面点D是投影点有垂直关系，另一方面出现一个定点A，由此我们在寻求另一定点就水到渠成.

2.如何找到直线MN恒过定点的坐标

通过直线MN特殊位置的任意两条直线的交点确定直线MN恒过定点的坐标，比如直线MN的斜率不存在、通过原点及与切线垂直等极端情况求之.

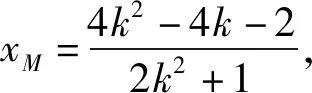
3.如何证明直线MN恒过定点

方法一：问题解析中的找到m，k的关系，利用直线的点斜式求之，是一种由一般到特殊的处理思路，将二元参数问题向一元参数化简消参的思想方法；问题的另一种处理方式，巧设直线方程结构形式，利用常数“1”代换，齐次化构造一元二次方程整体处理数据，是解决两动直线斜率之和与之积问题的有效途径.

方法二：由特殊到一般的数学思想方法，先根据特殊位置寻求到定点坐标，再利用三点共线的知识证明，比如转化到两直线的斜率相等，两向量共线问题等处理，这是问题途径3的求解方法.

4.基于直线MN恒过定点，如何寻求射影点D的轨迹方程

求解曲线轨迹方程的方法有定义法，条件直译法，相关点代入法，消参法(交规法)等，就本题来说，我们可以采用定义法——圆的定义，也可采用消参法——配方法消参及三角换元消参.

下面我们给出一种三角换元的消参方法，相当于引入角元，令k=tanα，

5.问题的一般性结论及其证明

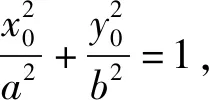
类似可以证明下列相关拓展问题：

本题蕴含数学核心素养之直观想象，试题仅仅给出问题缺少配图，其目的就是考查学生的作图技能，尽量把图作规范精确，易于解题的角度去绘制图象；对数学核心素养之数学运算的考查，需要引入两个点的坐标四个参数，加之设直线方程的斜率与纵截距形式两个参数，共计6个参数，参数多，运算量大，需要整体思想的结构式处理.在求解探索过程中，可以有效地的激发学生的创新潜能，增强学科内的知识层面及思维层面的拓展与融合.教学中尊重学生主体地位，优化学生思维品质及提升教师数学素养，知识与方法的深度融合.