新课标下立体几何教学方向探索——以2021年全国甲卷为例

安徽 查道丽

2021年安徽省高考理科数学使用全国甲卷.与往年相比，2021年高考全国甲卷理科数学试题的试卷结构保持不变，考查内容基本一致，体现了高考的稳定性与延续性；注重基础知识，体现数学思想，考查数学运算、应用、创新等能力.突出对数学抽象、逻辑推理、数据分析等核心素养的重视和“回归教材”等特点.题目看上去简单，实则不容易，对教学有很大的研究和参考价值.

一、概述

立体几何模块的考查在整张试卷中占有27分的分值，试题以“一大三小”的形式呈现.小题均是选择题，考查三视图、空间线线位置关系三棱锥外接球.大题是第19题分两小题设问，第(1)问证明线线垂直，第(2)问求二面角的正弦值最值问题.比较6年(2016-2021年)，2021年以前立体几何分值保持22分，2021年分值增长到27分.6年来解答题第(1)问考查均是证明问题，第5次考查垂直证明，6年中没有考查平行证明问题，并且2021年考查垂直，首次考查线线垂直,前5年解答题第(2)问考查都是二面角，2021年也不例外，理科考查风格基本没变.

二、真题分析

立体几何为数学的主干知识之一，一般情况下得满分有一定的难度.做这类题不确定的因素较多、难度较大、综合性较强，超出考生的想象.下面对此次高考立体几何部分试题一一分析.

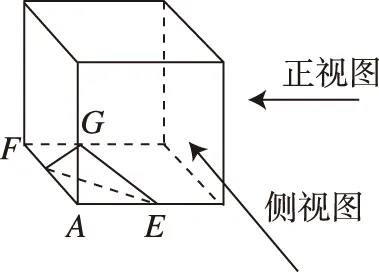
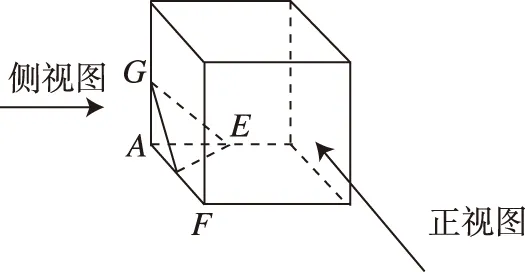
【例1】(2021·全国甲卷理·6) 在一个正方体中，过顶点A的三条棱的中点分别为E，F，G．该正方体截去三棱锥A-EFG后，所得多面体的三视图中，正视图如图所示，则相应的侧视图是

( )

【分析】本题考查三视图，根据题意及题目所给的正视图还原出几何体的直观图，学生在作图时，根据正视图可能会还原出两个直观图，结合直观图分清视图方向进行判断.考查立体几何必备知识的基础性.

解：如图，答案选D.

( )

A.346 B.373 C.446 D.473

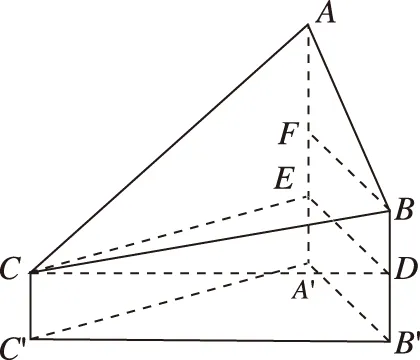
【分析】挖掘题目信息，找出隐含信息(AA′∥BB′∥CC′,AA′⊥平面A′B′C′)，通过数形结合，作图，结合解三角形来求解.不仅要关注条件是什么，也要关注问题是什么，只有双管齐下，才会事半功倍.

过C作CD∥C′B′交BB′于点D,过D作DE∥A′B′交AA′于点E,连接CE,过B作BF∥DE交AA′于点F.

故AA′-CC′=AE=AF+100=BF+100=A′B′+100.

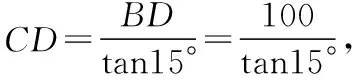
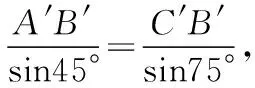
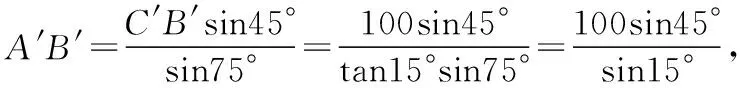
sin15°=sin(45°-30°)=sin45°cos30°-cos45°sin30°

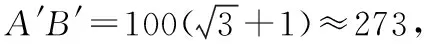
则AA′-CC′≈373.

【例3】(2021·全国甲卷理·11) 已如A，B，C是半径为1的球O的球面上的三个点，且AC⊥BC，AC=BC=1，则三棱锥O-ABC的体积为

( )

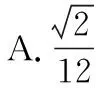
【分析】为求三棱锥O-ABC的体积，只需求球O到底面ABC的距离，熟悉球心与截面圆的关系，解题的关键是正确利用截面圆半径、球半径、球心到截面距离的勾股关系求解.从题目条件出发，建立关系式得出结论.

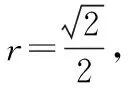
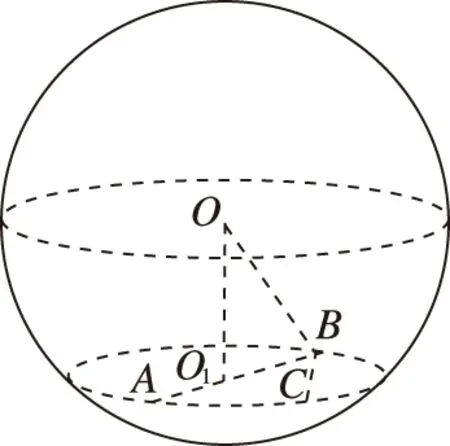
【例4】(2021·全国甲卷理·19) 已知直三棱柱ABC-A1B1C1中，侧面AA1B1B为正方形，AB=BC=2，E，F分别为AC和CC1的中点，D为棱A1B1上的点，BF⊥A1B1.

(1)证明：BF⊥DE；

(2)当B1D为何值时，面BB1C1C与面DFE所成的二面角的正弦值最小?

【分析】证明垂直就是要找出题目条件中所有的垂直关系，再结合判定定理证明即可；也可以通过建立空间直角坐标系来证明垂直、平行关系；求解二面角的平面角，直接方法是建立空间直角坐标系，也可以通过几何方法，作出二面角的平面角，结合解三角形来求解.

解法一：(1)因为三棱柱ABC-A1B1C1是直三棱柱，所以BB1⊥底面ABC，所以BB1⊥AB,

因为A1B1∥AB，BF⊥A1B1，所以BF⊥AB，

又BB1∩BF=B，所以AB⊥平面BCC1B1.

本方法适用于普通的砖烟囱施工，投入的施工人员和设备较少，材料简单，具有施工成本低、速度快、安全方便等特点，有一定的应用价值。

所以BA,BC,BB1两两垂直.

以B为坐标原点，分别以BA,BC,BB1所在直线为x,y,z轴建立如图所示空间直角坐标系,

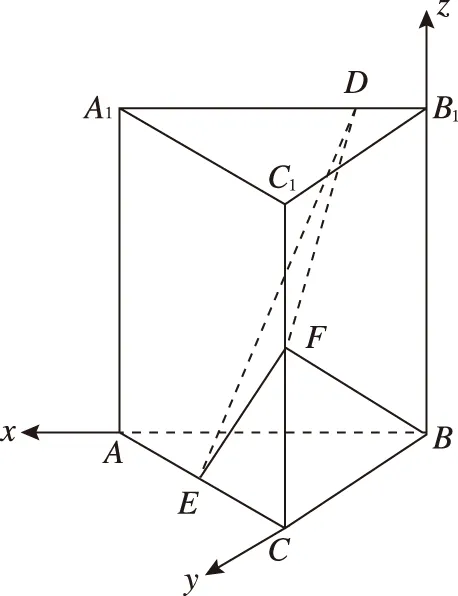
所以B(0，0，0)，A(2，0，0),C(0，2，0)，B1(0，0，2)，A1(2，0，2)，C1(0，2，2)，

E(1，1，0)，F(0，2，1).

由题设D(a，0，2)(0≤a≤2)．

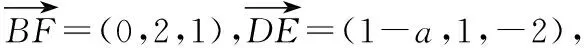
所以BF⊥DE．

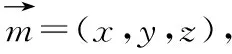
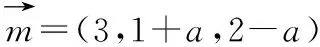
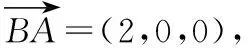
设平面BCC1B1与平面DEF的二面角的平面角为θ，

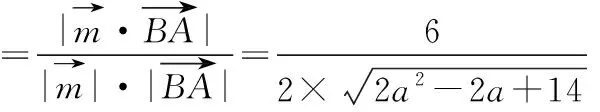
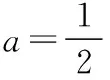
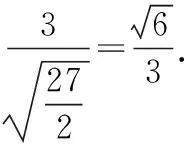
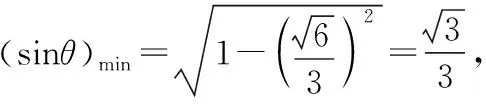
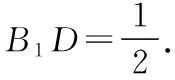
解法二：(1) 因为BB1⊥平面ABC,

所以BB1⊥AB.

又AB∥A1B1,A1B1⊥BF,

所以BF⊥AB.

又BB1∩BF=B,

所以AB⊥平面BB1C1C.

又AB⊂平面ABC,

故平面ABC⊥平面BB1C1C.

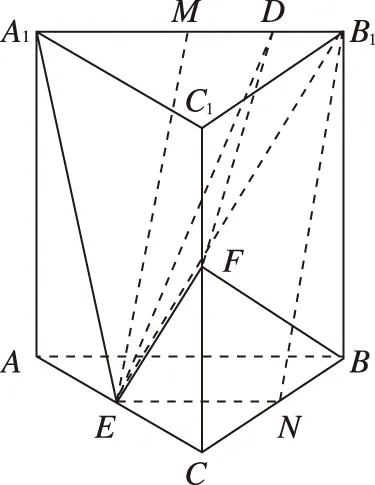
设A1B1的中点为M，连接EM，过E作EN∥AB交BC于点N，连接B1N易知ENMB1,则四边形ENB1M是平行四边形，EM∥NB1.

△BCF≌△B1BN,

所以∠FBC+∠B1NB=90°,

故FB⊥B1N,

所以FB⊥EM,

又EM∩A1B1=M,

所以FB⊥平面A1EB1,

因此FB⊥DE.

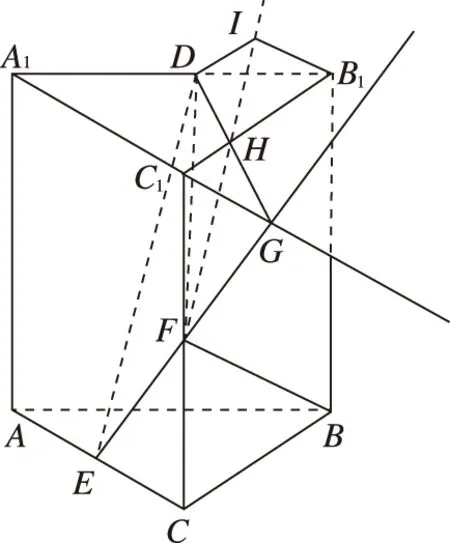
(2)分别延长EF,A1C1相交于点G，连接DG并与B1C1交于点H，连接HF，过B1作HF的垂线交于FH延长线上一点I，连接DI.

因为FH⊂平面DEF，FH⊂平面BB1C1C,

所以平面DEF∩平面BB1C1C=FH.

由(1)证明知AB⊥平面BB1C1C，则A1B1⊥平面BB1C1C，所以DB1⊥平面BB1C1C，因此DB1⊥FH.

因为B1I⊥FH，B1I∩B1D=B1，

所以FH⊥平面B1DI，

又FH⊥DI，

所以锐角∠DIB1是平面DEF与平面BB1C1C的夹角.

易知△B1IH∽△FC1H，

易知△GC1H∽△GKD,

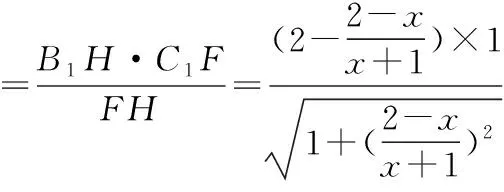
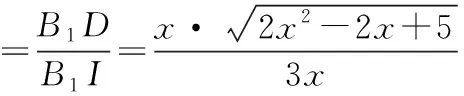
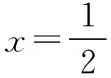
对于此题，综合法与坐标法相比，复杂且不直观，但从数学素养的培养角度，综合法能够锻炼学生的直观想象、逻辑推理、数学运算等数学核心素养，对数学学习能力以及兴趣的培养都具有积极意义.

三、教学反思

对于数学学习，尤其对平面几何、立体几何，从“形”入手，直观助思；从“数”突破，验证直觉.本卷考查锥体、球体以及线线、线面、面面关系，两面所成角等知识，以及数形结合、化归与转化等思想方法.考生的思维障碍在于根据题意作出图形助思.显然，图形更有利于考生思考、解决问题.求空间角包括求两条异面直线所成角、线面角和面面角，求解的基本路径是：“找(作)—说—求”.“找”是关键，没有现成的就需要“作”，作线线角重点是“平移直线”；作线面角重点是“线面垂直”；作面面角重点也是“线面垂直”.

按照题目问题状态，可以分为“题给图形”和“自构图形”两种基本类型.学生的主要问题是：一是没有想到数形结合；二是构图马虎，不能达到“助思”效果；三是构图不够“常态”，产生误导.

数形结合是高中数学的核心思想方法之一.从“形”入手、用数形结合的思想方法，是解答选择、填空题的重要策略；而由“数”联想到“形”，是一种创造、创新，对学生本身是一个“坎”.建议高三复习时选用恰当的问题进行数形结合的思想立意；同时，结合距离、斜率等数式的几何意义，创造机会让学生思“形”，增长数形结合、由“数”思“形”的见识，激发学生的创新思维.

符合高考命题理念，从原来的“知识立意”“能力立意”向“价值引领、素养导向、能力为重、知识为基”转变.

我们在教学中特别注意以下四点：

(一)在教学中一定要充分备课、备好课，尽力让学生理解教材的概念、性质、定理等，要强化学生对基础题的训练，理解和训练一定要双管齐下，只有熟练知识点才可能实现知识点的融会贯通.以本试卷立体几何为例，虽然要求学生具备一定的空间想象能力，但是如果没有解三角形的知识作储备，立体几何很难做出来.

(二)我们在新授课中一定要充分备课、备好课，积极发挥学生的主观能动性.每章节的结束，让学生自己及时总结归纳知识、方法以及数学思想， 反思自己的得与失，调动他们学习的积极性与主动性，这对于学习很有帮助.本卷的立体几何，如果能熟练运用数形结合，做满分并不是可望不可及.

(三)我们一定要充分备课、备好课，重视试卷分析课，提高审题质量.好的试卷分析课能够帮助学生从解题没思路快速成长为做题有思路；在有思路的情况下影响得分的主要是表述规范、隐含条件运用以及与其他知识点交汇考查综合应用能力等问题，在分析试卷时，我们需要平时就要求学生认真审题，规范答题，养成良好的答题习惯.

(四)“超低空、地毯式、拉网式”的复习策略.一定要回归课本，做到知识、方法、思想全覆盖.在内容上，要及时总结归纳知识和方法；在对课后习题处理上，要取其课本上的精华；严格要求自己，做到遍地撒网.虽然理科历年来考证明平行位置关系的问题少，且解答题考的是二面角和线面角，线线角没出现在解答题，但选择填空题历年来有考，虽今年不考，不代表以后不考，我们在复习时一定要全面.