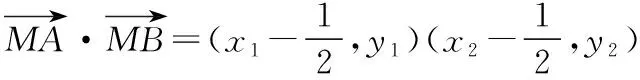创新性优秀原创试题选登

山东 丛以权 广东 龙 宇 黑龙江 李伟胜

1.【研发题】

为纪念中国共产党成立100周年，加深青少年对党的历史、党的知识、党的理论和路线方针的认识，激发爱党爱国热情，坚定走新时代中国特色社会主义道路的信心，某校举办了党史知识竞赛.竞赛规则是：两人一组，每一轮竞赛中，小组两人分别各答3道题，若答对题目总数不少于5道题，则获得一个积分.已知甲、乙两名同学一组，甲同学和乙同学每道题答对的概率分别是p1和p2，且每道题答对与否互不影响.

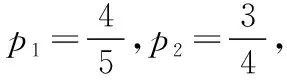
【考查目标】

本题主要考查二项分布与导数的综合，要求学生能从生活实践或学习探索层面的问题情境中提炼出数学问题，并解决问题，考查数据处理能力、运算求解能力，落实数学运算的核心素养.

【名师指导】

(1)利用所给数据和互斥事件的概率求值;(2)根据(1)形成p1p2=t的函数p(t),对函数求导，求出函数的最大值，再由np≥5即可求出所求.

【解题思路】

(1)设同学甲和同学乙答对的题目个数分别为a1和a2，所以所求的概率

P=P(a1=2,a2=3)+P(a1=3,a2=2)+P(a1=3,a2=3)

(2)他们在一轮竞赛中获得一个积分的概率

P=P(a1=2,a2=3)+P(a1=3,a2=2)+P(a1=3,a2=3)

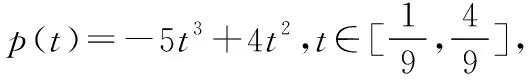
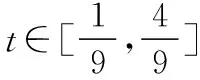
甲、乙两同学在n轮竞赛中获得的积分数X满足X～B(n,p)，

所以若甲、乙同学想至少获得5个积分，理论上至少要进行15轮竞赛.

2.【研发题】

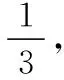
(1)若n=2，求分数X的分布列;

【考查目标】

本题考查随机变量的分布列及确定目标下的概率等相关知识，同时考查了数列的递推性质，数学归纳法的思想以及“非线性规划”等一系列知识.考查了运算求解能力，数据分析以及数学建模等能力，落实了数据分析、逻辑推理等数学核心素养.

【名师指导】

(1)先确定n的取值，然后确定X的取值，求出其概率，进而求得分布列;(2)设G(m)≥G(1)求出p与q的关系，再利用“线性规划”的思想考虑如下：根据两个条件，可得点(p,q)的可行域：结合q的取值范围求证.

【解题思路】

(1)当n=1时，X的取值可能为0,1,2,

当n=2时，X的取值可能为0,1,2,3,4,

X01234P(1-13p-23q)22p3(1-13p-23q)4q3(1-13p-23q)49pq49q2

不妨设当k≤m时，G(k)≥G(1)成立，现考虑k=m+1时的情况;

对于G(m+1)，其值为G(m+1)=G(m)G(1)+G(m-1)G(2)；

令G(m+1)=G(m)G(1)+G(m-1)G(2)≥G(1)，根据假设G(m)≥G(1)，G(m-1)≥G(1)，

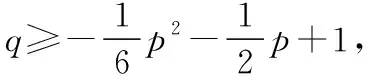
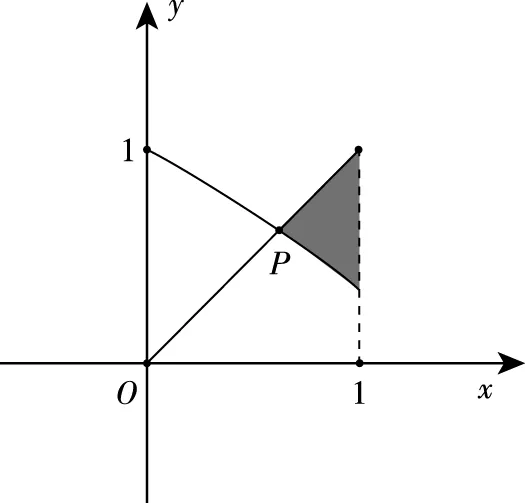
图1

图2

3.【研发题】

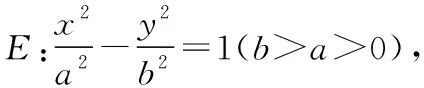
(1)求双曲线E的方程;

问题：是否存在过右焦点的直线与双曲线E的右支相交于A,B两点，________，使得∠AMB为直角？

【考查目标】

本题以圆锥曲线为背景，考查直线与双曲线位置关系的问题，考查数学运算、逻辑推理的数学核心素养.

【名师指导】

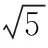
【解题思路】

(2)方案①：令A(x1,y1),B(x2,y2)，

若直线AB与x轴不垂直，设直线AB的方程为y=kx-3k(k≠0)，

可得 (5-4k2)x2+24k2x-4(9k2+5)=0，Δ>0

由题意可知A，B两点都在双曲线的右支上，

因为∠AMB为直角，所以AM⊥BM,

=0,

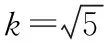
方案②：令A(x1,y1),B(x2,y2),

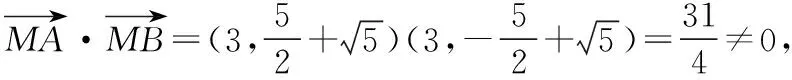
若直线AB与x轴不垂直，设直线AB的方程为y=kx-3k(k≠0),

可得(5-4k2)x2+24k2x-4(9k2+5)=0,Δ>0，

由题意可知A,B两点都在双曲线的右支上,

因为∠AMB为直角，所以AM⊥BM,

方案③：令A(x1,y1),B(x2,y2),

所以直线AB的方程为x=3.

若直线AB与x轴不垂直，设直线AB的方程为y=kx-3k(k≠0),

可得(5-4k2)x2+24k2x-4(9k2+5)=0.

由题意可知A,B两点都在双曲线的右支上,

因为∠AMB为直角，所以AM⊥BM,