回归基础 突出能力 聚焦思想
——2021年新高考Ⅰ卷试卷分析与教学思考
2021-11-09江苏张朋举
江苏 张朋举
2020年是江苏自主命制高考试卷的收官之年,2021年是江苏高考使用新高考Ⅰ卷的元年;整份试卷以素养立意,原创为本,层次分明,亮点纷呈,体现出试题有效性、导向性、公平性和创新性的和谐统一;但这份试卷和去年的山东卷和八省联考卷相比变化还是比较大,首先试卷的阅读量有所下降,原有的开放题、结构不良题没有出现(但全国卷甲、乙卷及新高考Ⅱ卷均有出现),总体感觉试卷更平和,试题基本上按照由易到难的顺序推进;其次题目更显中规中矩,易中难比例真正做到了5∶3∶2,但很多试题需要学生对数学本质有所理解,要关注方法的选择,方法选择不好,耗时费力,得高分难;其实,针对新一轮的课程改革,教育部考试中心早就出台了《中国高考评价体系》,该体系明确了“一核”“四层”“四翼”的概念,明确了高考主要以“立德树人、服务人才、引导教学”为核心功能,并从“一核”“四层”“四翼”三个方面回答了“为什么考、考什么、怎么考”的考试本源性问题,给出了“培养什么人、怎样培养人、为谁培养人”这一教育根本问题在高考领域的答案.纵观这份试卷较好地体现了新高考评价体系要求,契合了学科的培养目标,引导了今后高考数学试卷的方向,对今后的教学起到正面的积极的引导作用.以下笔者结合具体试题,谈谈体会.
1.试卷特征
1.1 突出数学主干知识的考查
高中阶段,数学的主干知识主要有预备知识(集合、简易逻辑、不等式等)、函数、几何与代数、概率与统计、数学建模活动与数学探究活动等内容,试题突出主干知识的考查,同时考查考生的数学思维能力,灵活运用所学知识解决问题的能力.这也启示我们平时要重视教材的使用,尤其高三的后期,回归教材显得尤为重要;笔者按照新课标四大主题内容,对该试卷进行了简单汇总,预备知识占5分,函数占52分,几何与代数占71分,概率与统计占22分,主干知识占135分,占全卷的90%,基本实现主干知识全覆盖;另外,也有部分试题涉及多个知识点,比如试卷第5题以椭圆为载体,不仅考查了椭圆的定义,也很好地考查了基本不等式、求函数最值等知识点;具体分布如表:
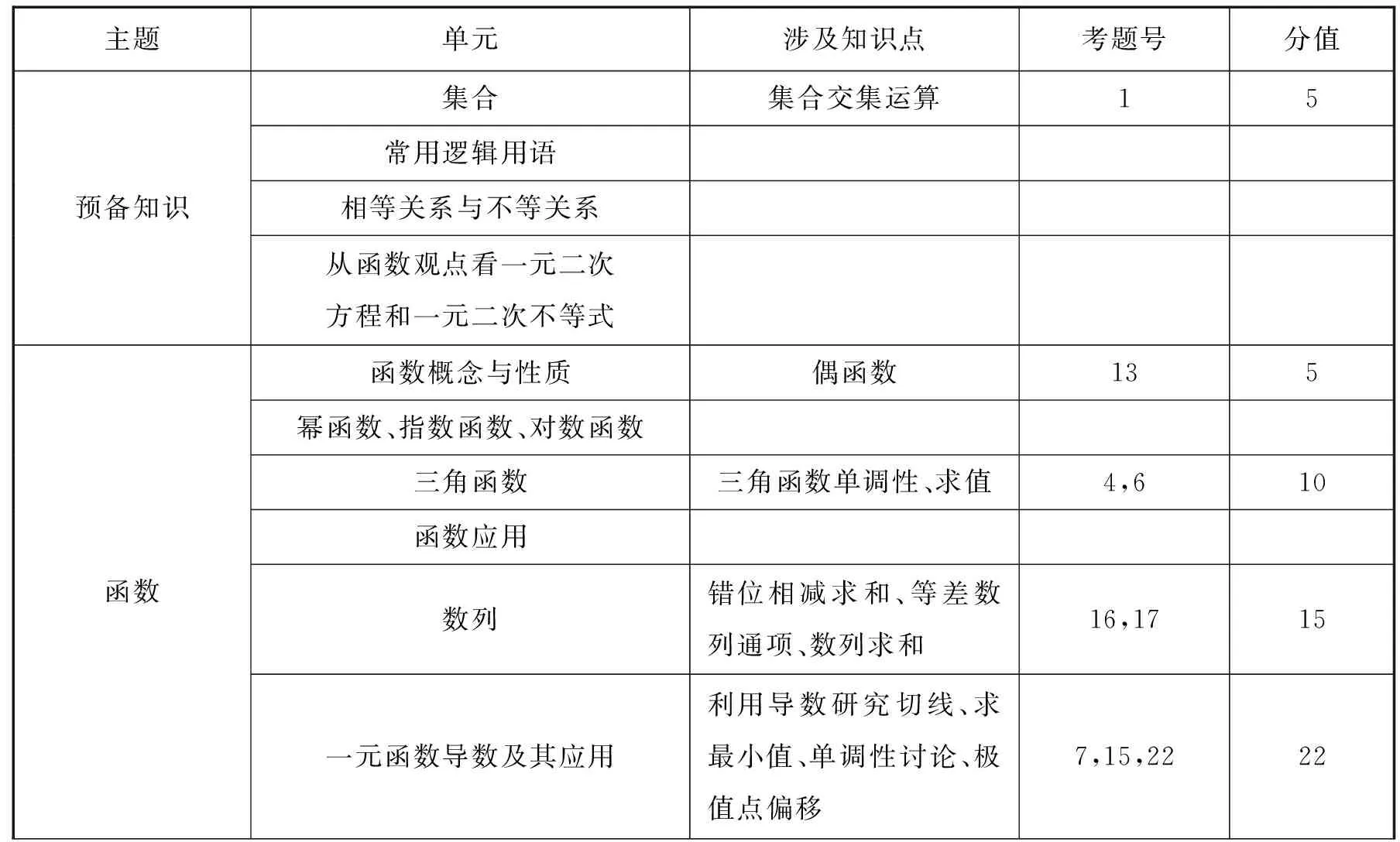
主题单元涉及知识点考题号分值预备知识集合集合交集运算15常用逻辑用语相等关系与不等关系从函数观点看一元二次方程和一元二次不等式函数函数概念与性质偶函数135幂函数、指数函数、对数函数三角函数三角函数单调性、求值4,610函数应用数列错位相减求和、等差数列通项、数列求和16,1715一元函数导数及其应用利用导数研究切线、求最小值、单调性讨论、极值点偏移7,15,2222
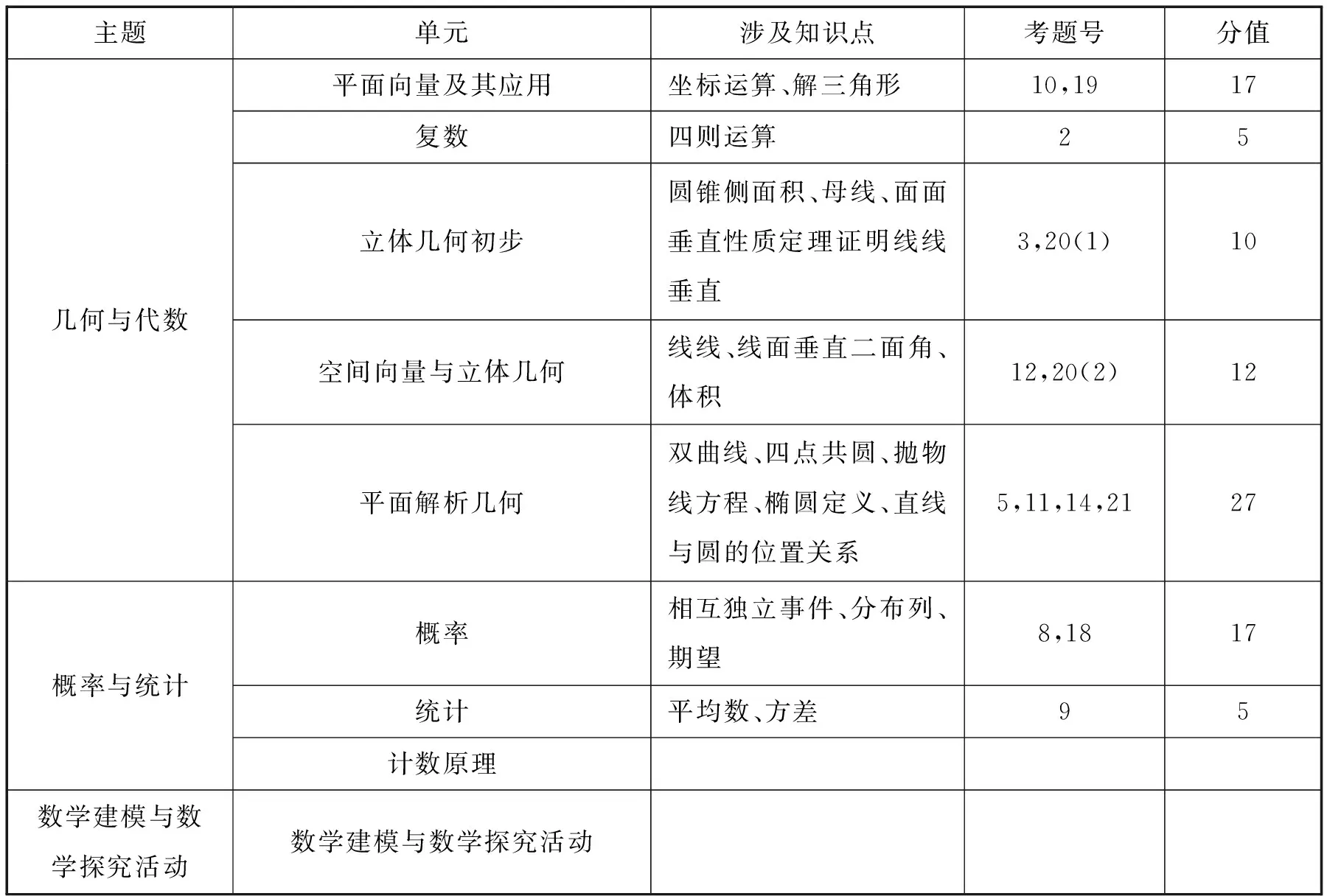
续表
【例1】(2021·新高考Ⅰ卷·8)有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则
( )
A.甲与丙相互独立 B.甲与丁相互独立
C.乙与丙相互独立 D.丙与丁相互独立
评注:本题主要考查概率与统计模块中两个随机事件A,B相互独立的定义,课标中要求学生了解该定义;近些年,高考试卷中主要考查利用独立性计算概率,很少涉及对判断两个事件相互独立的知识点考查,其实判断方法主要有三种:1.直观感觉(观察);2.定义判断;3.充要条件:P(AB)=P(A)P(B);其中充要条件P(AB)=P(A)P(B)比较常用.
1.2 侧重数学思想的运用
思想是方法的升华,解决数学问题的灵魂就是思想;学数学知识需要数学思想,数学基本思想方法主要涉及数形结合、化归与转化、分类讨论、方程、建模、类比、归纳推理、极限等思想方法.基于重要的数学思想方法命题是命制高考试题最基本方式之一,随着课改的深入,这种命题不仅考查学生的数学思维及解决问题的能力,还体现了数学学科的本质,引领教学的方向.数学思想方法的形成和发展是需要长期的过程,需要教师在教学中,经常性的渗透数学思想方法;比如2021年数学新高考Ⅰ卷第11题涉及数形结合,第15,17题涉及分类讨论,第16题涉及归纳推理,第21题涉及基本活动经验,第二问涉及条件|TA|·|TB|=|TP|·|TQ|的等价转化等.
【例2】(2021·新高考Ⅰ卷·11)已知点P在圆(x-5)2+(y-5)2=16上,点A(4,0),B(0,2),则
( )
A.点P到直线AB的距离小于10
B.点P到直线AB的距离大于2


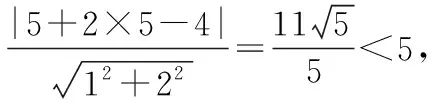
评注:数形结合就是在解决数学问题时,由数思形、以形思数、数形结合考虑问题,本题是数形结合思想体现的典范.
1.3 关注数学核心素养的体现
高中数学课程标准对培养学生能力的要求,由开始的“四基”到“四能”,演变到现在的“六大核心素养”;高考试题不仅可以很好地考查“四基”“四能”,更是数学六大核心素养的集中展示;要检验学生核心素养高低,必须通过解决数学问题来体现;事实上,学生可以通过解决数学问题,实现用数学的眼光观看客观世界(数学抽象、直观想象),用数学的思维思考现实世界(逻辑推理、数学运算),用数学的语言表达现实世界(数学建模、数据分析)等.比如2021年数学新高考Ⅰ卷第7题考查了直观想象、逻辑推理核心素养,第9题考查了数据处理、数学运算核心素养,第12题考查直观想象、逻辑推理核心素养,第21题考查逻辑推理、数学运算等核心素养.
【例3】(2021·新高考Ⅰ卷·7)若过点(a,b)可以作曲线y=ex的两条切线,则
( )
A.eb
C.0
解析:过(a,b)可以作曲线y=ex的两条切线,则点(a,b)在曲线y=ex的图象下方,且在x轴上方,所以0
评注:数学学科的核心素养是数学课程目标的集中体现,是在数学学习和应用中逐步形成和发展起来的,核心素养该怎样考?本题给出了答案,其很好地考查了学生的直观想象能力,几何直观的本质是将相对复杂、抽象的问题“图形化”,让学生形成数学直观,在具体试题解决中感悟数学的本质.
1.4 重视数学知识本质的把握
《普通高中数学课程标准(2017年版2020年修订)》在课程基本理念中指出:“把握数学本质,启发思考,改进教学”.本质语出晋代刘智《论天》:“言闇虚者,以为当日之冲,地体之荫,日光不至,谓之闇虚.凡光之所照,光体小於蔽,则大於本质.”数学是一门研究规律的学科,有其内在的根本属性和规律,而这个根本属性与规律就是数学本质.学生通过对高考试题,一题多解,体会和认识问题的数学本质,探究数学问题解决的基本规律,理解数学、感受数学研究的“味道”,学会 “数学思维”;比如数列问题的本质是归纳、猜想、推理,16,17两题正是考查这点,解决解析几何问题的方法本质是图形问题代数化,14,21两题也正考查了圆锥曲线的核心方法,其中21题以双曲线为背景,更是要求学生运用解析几何的基本思想和方法分析和解决问题.
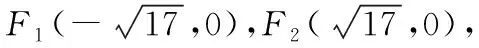
(1)求C的方程;
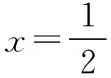
解析:(1)略
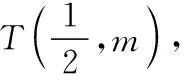
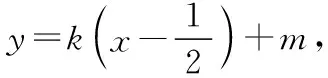

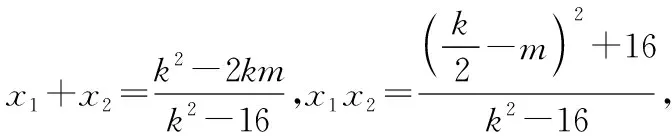
故设TA,TP的斜率分别为k1,k2,(k1≠k2).
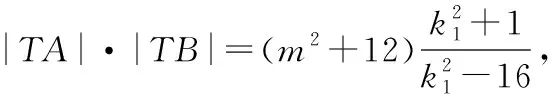
由|TA|·|TB|=|TP|·|TQ|,
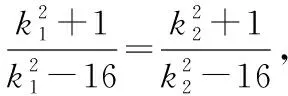
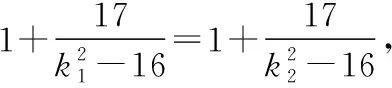
又k1≠k2,故k1+k2=0.
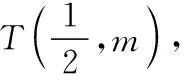
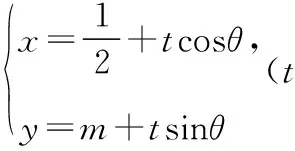
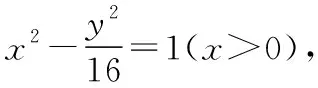
整理得(17cos2θ-1)t2+(16cosθ-2msinθ)t-12-m2=0,
设t1,t2是这个方程的两个根,
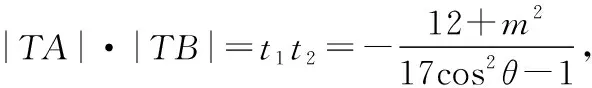
设直线PQ的倾斜角为α,α∈(0,π),
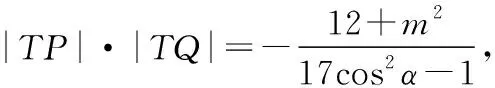
由|TA|·|TB|=|TP|·|TQ|,
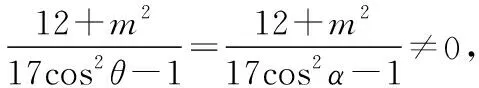
则17cos2θ-1=17cos2α-1,cosθ=±cosα,
又由α,θ∈(0,π),且α≠θ,
所以cosθ=-cosα,θ+α=π,
直线AB的斜率与直线PQ的斜率之和为0.
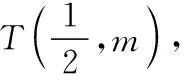
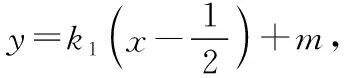

所以A,B,P,Q四点的坐标满足方程
又由A,B,P,Q四点还在曲线C上,所以由曲线系方程得,A,B,P,Q四点在曲线

由|TA|·|TB|=|TP|·|TQ|,根据圆的双割线定理的逆定理可知,A,B,P,Q四点共圆,所以曲线
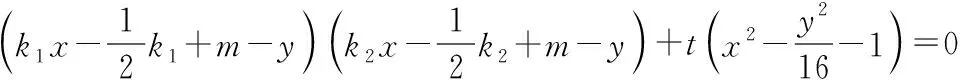
所以x2,y2的系数相等,且xy系数为0,即k1+k2=0.
评注:学生抓不住“|TA|·|TB|=|TP|·|TQ|”的本质,不会对其进行多元表征,易出现思维混乱;实际上,设过点T的直线方程(方法1),利用弦长公式化简,对计算能力要求较高,若引入直线参数方程(方法2)或利用曲线系(方法3),可以很好地回避了繁琐的运算,而且利用二次曲线系方程,也很好地揭示了A,B,P,Q四点共圆这一隐藏本质.
2.对教学的几点思考
2.1 关注精准教学,落实教学评一致
精准教学包括两个方面,一方面指基于课标分解,即将《课程标准》中的内容标准具体细化为学期或模块目标、单元或课时目标.课标分解的基本特点是将抽象的内容标准分解为具体可操作的教学目标,将长时段需要达成的大目标分解到短时间如单元或课时可以达成的小目标,将隐性的素质目标显化为可以观察和评价的行为目标.让子目标引领课堂教学活动设计和学生活动,使课堂教学活动设计更具有针对性.另一方面指基于目标达成情况的评价分析,即制定每一个子目标达成情况的标准,依据标准对目标的达成情况进行精准分析,反馈课堂教学,指导教师及时调整教学策略.
笔者认为,平日教学中,教师应以新课标、新高考评价体系为指导,通过对高中数学课程标准的逐级分解,形成以新高考评价体系为依据的教学设计方案(包括制定目标、实施路径、实施方法、反馈练习)与教学评价方案,对方案进行课堂实践和效果评估,进而提高课堂的教学质量,落实教、学、评一致.
2.2 关注作业设计,落实教、学、评一致
作业一词由来已久,在不同场合使用其意义不同,《辞海》认为,作业是为了完成生产学习等方面的既定任务而进行的活动.作业问题归根到底就是设计什么、多少作业问题.当下,在高中数学教学实践中,由于教师普遍存在“题海战术”的认识,导致学生的作业繁重、难度偏大,甚至出现课后作业的内容与学生所学内容不一致的情况,教师对作业有效度的轻视几乎是个致命伤,总以为只要多做练习就能提高教学质量;批改的少,反馈的少,取而代之的是午练、晚练,及千人一面的“一课一练”.
新高考的命题主要围绕数学内容主线,考查学生的数学思维和素养,注重体现数学本质和通性通法;盲目通过增多作业量已经不能起到应有的效果;实际上,教什么、学什么、考什么三者应该具有高度的相关性;教到什么程度、学到什么程度、考到什么程度是一致的;教学设计、教学实施、教学效果是一致的.为了充分发挥高考引领教学,笔者倡导作业设计应基于不同授课类型精准指向基本知识、基本思想方法、认知结构、数学探究等.
2.3 关注解题教学,落实教授学生学思考

