地震反应谱长周期分量对大跨度桥梁地震反应的影响

宋爱民， 常付平， 叶爱君

(1. 同济大学 土木工程防灾国家重点实验室， 上海 200092； 2. 上海市政工程设计研究总院(集团)有限公司， 上海 200092)

目前，世界各国的桥梁抗震设计规范都将反应谱法作为地震反应分析的基本方法，但是由于缺乏真实有效的长周期地震记录，各国抗震规范只对自振周期较短的结构给出了反应谱计算公式[1,2]。欧洲抗震设计规范NF P06-030-1/NA-2013《Eurocode 8: Design of Structures for Earthquake Resistance》规定了自振周期在4 s之前的加速度反应谱计算公式，建议4 s后的加速度反应谱由位移反应谱值根据拟谱关系得到[3]；美国桥梁抗震设计指南《AASHTO Guide Specifications for LRFD Seismic Bridge Design》规定的加速度反应谱无最大周期的限制，但指出当结构自振周期超过3 s后，规范规定的加速度反应谱谱值会偏保守[4]；我国JTG/T 2231-01-2020《公路桥梁抗震设计规范》(以下简称《公规》)规定的加速度反应谱最大周期为10 s[5]，CJJ 166-2011《城市桥梁抗震设计规范》(以下简称《城规》)的设计加速度反应谱引自GB 50011-2010《建筑抗震设计规范》(以下简称《建规》)，规定的加速度反应谱最大周期为6 s[6]。

近年来，我国兴建了众多的大跨度索支撑桥梁，基本周期常常超过10 s[7,8]，采用设计规范反应谱进行地震反应分析存在长周期谱值的确定问题。在实际工程中，为提高结构的抗震安全度，往往对规范的设计加速度反应谱曲线超出周期范围部分做平台化处理，但这会导致结构的地震反应过大，设计过于保守。

为了建立长周期结构的设计反应谱，国内外学者做了一些研究。耿淑伟等[9]通过对实际观测的955条地震动记录进行统计分析，以均方误差最小原则拟合标准化反应谱，建议对于周期T大于6 s的加速度反应谱按T-1的速率下降到10 s。方小丹[10]根据位移反应谱与加速度反应谱的拟谱关系，对《建规》规定的加速度反应谱下降段进行了修正，建议加速度反应谱第一下降段(速度下降段)可简单地按照T-1的规律衰减，第二下降段(位移下降段)按照T-2的规律衰减，并将反应谱周期延长至10 s。邱立珊[11]基于汶川地震记录的远场长周期地震动，对《建规》加速度反应谱第二下降段特征点周期及谱曲线进行修正，提出了包含5个待标定参数的长周期加速度反应谱模型，直至10 s。

为了分析地震加速度反应谱的长周期分量对大跨度桥梁地震反应的影响，本文首先对中美桥梁抗震设计规范的地震加速度反应谱的长周期部分进行比较分析，然后基于实际地震记录的加速度反应谱，对我国《城规》的加速度反应谱长周期部分提出修正建议。接着，以一座主跨428 m的三塔自锚式悬索桥为例分析地震加速度反应谱长周期分量对桥梁结构不同地震反应分量的影响，并检验修正建议的合理性，以期供工程实践参考使用。

1 规范地震加速度反应谱的长周期分量取值建议

1.1 中美规范加速度反应谱与实际地震记录反应谱的比较分析

美国桥梁抗震设计规范《AASHTO Guide Specifications for LRFD Seismic Bridge Design》(以下简称《美规》)规定加速度反应谱如式(1)所示。

(1)

式中：SDS，SDI分别为周期0.2，1 s对应的设计加速度反应谱谱值，由场地条件决定；T0=0.2SDI/SDS；Ts=SDI/SDS。由式(1)可知，《美规》加速度反应谱长周期部分以T-1的规律衰减[4]。

我国《城规》的加速度反应谱谱值S如式(2)(3)所示。

(2)

Smax=2.25A

(3)

式中：A，Tg分别为地震峰值加速度与特征周期；η2为结构阻尼调整系数；γ，η1分别为特征周期至5倍特征周期区段曲线衰减指数和5倍特征周期至6 s区段直线下降段下降斜率调整系数[6]。

我国《公规》的加速度反应谱谱值S(T)如式(4)(5)所示。

(4)

Smax=2.5CiCsCdA

(5)

式中：T0为反应谱直线上升段最大周期，取0.1 s；Ci，Cs，Cd分别为结构重要性系数、场地系数与阻尼调整系数[5]。

根据《城规》确定一条加速度反应谱，其中，设计地震动加速度峰值为1.6 m/s2，特征周期为0.85 s，结构阻尼比为0.02，阻尼调整系数取1.47，γ与η1分别取1与0.02。以此加速度反应谱作为目标谱，在PEER数据库中挑选了7条实际地震动，具体信息见表1。七条实际地震动对应的加速度反应谱与其均值如图1所示。此外，根据《美规》确定一条加速度反应谱(周期0～15 s)，该反应谱前6 s的谱值与上述《城规》加速度反应谱接近；将《城规》加速度反应谱延长至15 s，其中 6 s后的谱值与6 s时相同；根据《公规》确定一条加速度反应谱(周期至15 s)，该反应谱前6 s的谱值与《城规》加速度反应谱接近，10 s后谱值与10 s时相同。图2给出《美规》、延长后的《城规》、延长后的《公规》加速度反应谱和实际地震动加速度反应谱的平均值对比，将上述4条加速度反应谱根据拟谱关系拟合成位移反应谱，如图3所示。

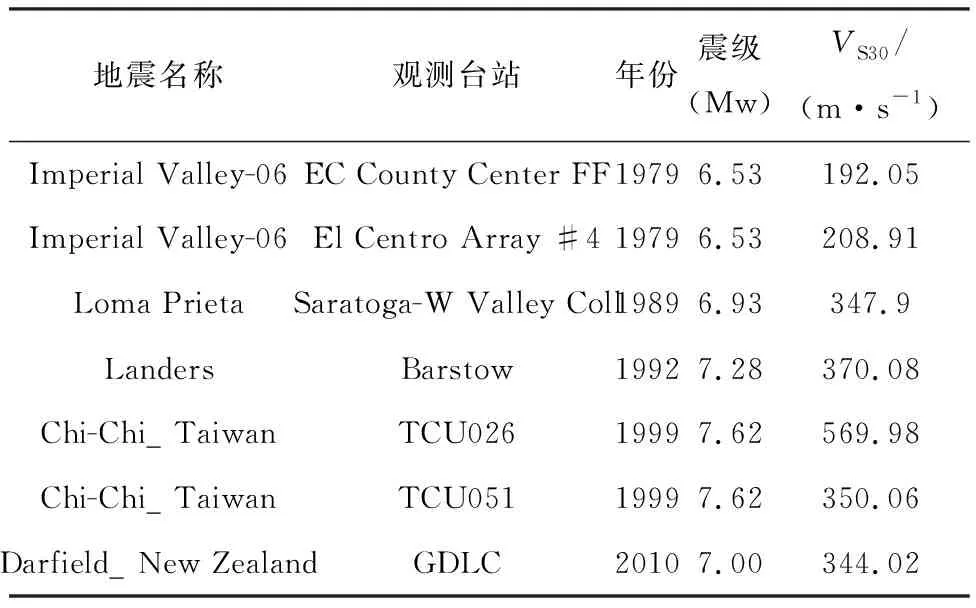
表1 强震加速度记录

图1 实际地震动加速度反应谱

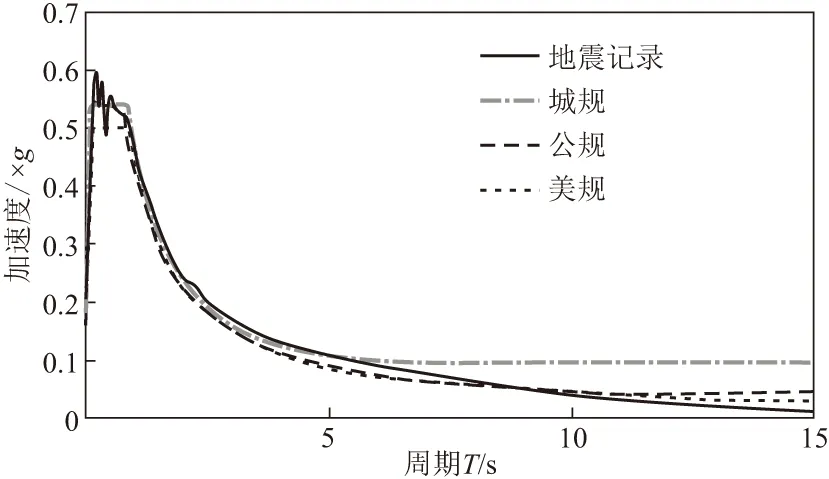
图2 加速度反应谱对比

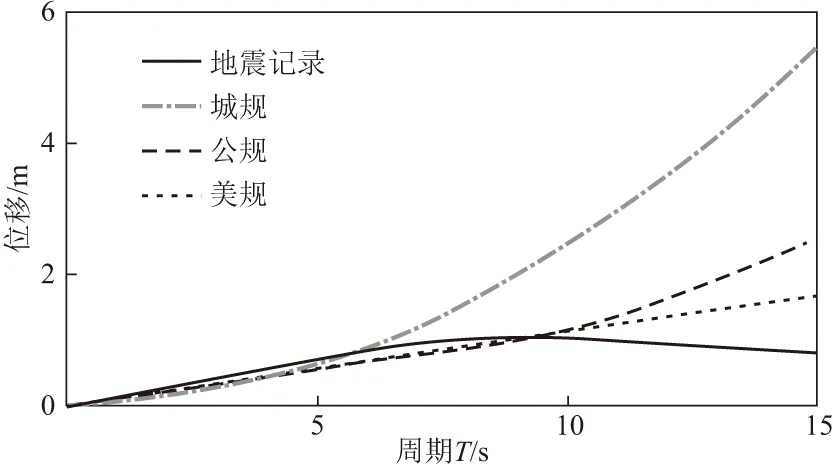
图3 位移反应谱对比

由图2可知，《城规》加速度反应谱如果长周期部分按平台化处理，则谱值比《美规》《公规》和地震记录加速度反应谱大很多，且差值随周期的增长不断变大；而《美规》和地震记录加速度反应谱在长周期段较为接近。可见，《城规》加速度反应谱如果长周期段取平台会过于保守，实际地震动加速度反应谱在长周期段近似为周期倒数的一次函数。由图3可知，《城规》加速度反应谱如果长周期段取平台，对应的位移反应谱在长周期段以T2的规律上升，上升规律明显不满足相对位移谱统计特征，且长周期段谱值远大于实际地震动位移谱值；《美规》对应的位移反应谱以周期一次函数的规律上升，《美规》在长周期段对地震记录位移谱模拟较好，且谱值略大于地震记录位移谱，具有一定的安全度。

1.2 《城规》加速度反应谱的长周期修正建议

现行《城规》只对自振周期在6 s之内的结构给出了反应谱计算公式，如果对规范设计反应谱超出周期范围部分取平台，则长周期部分位移谱会严重偏离实际。由于《美规》加速度反应谱长周期段以T-1规律衰减，对应的位移谱在长周期段对地震记录位移谱模拟较好，建议《城规》6 s后加速度反应谱按式(6)计算，其中，S6为6 s的加速度反应谱谱值。将《美规》、地震记录和建议的加速度反应谱对比，如图4所示。并将上述3条加速度反应谱根据拟谱关系拟合成位移反应谱，如图5所示。由图4，5可知，建议的《城规》加速度和位移反应谱长周期段稍大于《美规》，而且显著大于实际地震记录，已有足够的安全度。

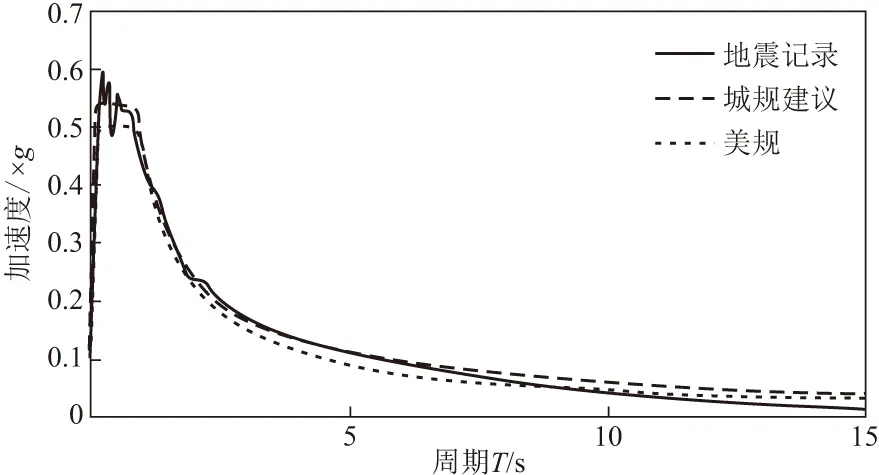
图4 加速度反应谱对比

图5 由拟谱公式得到的位移反应谱

(6)

2 大跨度桥梁计算模型及动力特性

为了定量分析反应谱长周期分量对大跨度桥梁不同地震反应分量的影响，本文以一座主跨为428 m的三塔自锚式悬索桥为例，建立了计算模型用于地震反应分析。

2.1 背景工程简介

某大跨桥梁采用三塔双索面组合梁自锚式悬索桥方案，全长约1332 m，跨径布置为：70+168+428+428+168+70=1332 m，如图6所示。主梁为钢-混凝土叠合梁结构，梁高4 m，标准段全宽58.7 m。三个桥塔均为A型塔，塔身为钢结构，塔座为混凝土结构，中塔塔身高114.58 m，塔座高9.09 m，边塔塔身高110.6 m，塔座高3 m。各塔(墩)均采用群桩基础，为钻孔灌注桩并按嵌岩桩设计，桩径为2.0 m。各塔(墩)与主梁间均设置纵向滑动、横向固定支座。

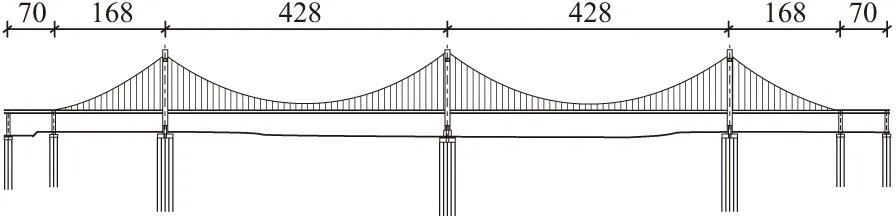
图6 主桥立面/m

2.2 动力分析模型

基于SAP2000平台，建立了该桥的有限元动力分析模型，建模时考虑了边界联对主桥的影响。总体模型如图7所示。主梁、主塔、塔座和承台根据实际截面尺寸以框架单元模拟；主缆和吊杆采用桁架单元模拟，并通过主从约束与吊杆相连接。主缆、吊杆和主塔考虑了恒载作用对结构几何刚度的影响，二期恒载以线质量的形式加在梁单元上[12]。采用六弹簧模型模拟各群桩基础的影响，如图8所示。各塔(墩)与主梁间纵向自由，横向固定约束，为漂浮体系。

图7 悬索桥动力分析模型

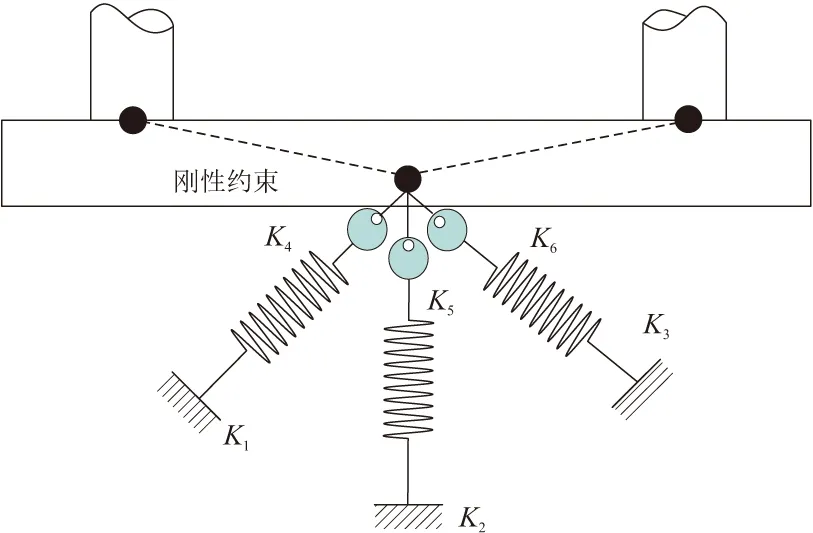
图8 群桩基础六弹簧模型

2.3 桥梁动力特性

对上述模型进行动力特性分析，表2给出了前5阶振型的周期和模态，结果表明：桥梁结构的基本周期(纵飘)为12.65 s，远大于《城规》反应谱的最大周期6 s。结构前5阶振型皆为纵向或竖向振动，故反应谱长周期分量对桥梁的纵向反应影响较为显著。

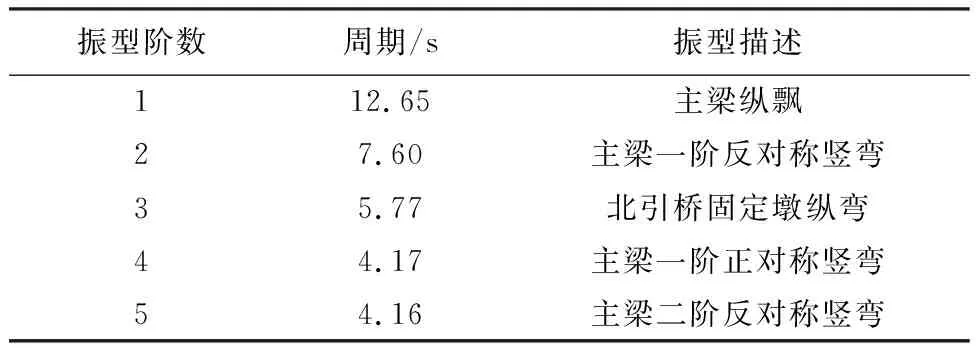
表2 某悬索桥结构动力特性

3 加速度反应谱长周期分量对大跨度桥梁地震反应的影响

本文基于前述计算模型，分别将现行《城规》(6 s后取平台)、《公规》(10 s后取平台)、《美规》、地震记录和《城规》(修订)的加速度反应谱作为地震输入，通过比较不同输入下的桥梁结构地震反应来分析加速度长周期分量对桥梁地震反应的影响。

在进行地震反应谱分析时，分别计算考虑600阶贡献和仅考虑基本振型贡献桥梁结构的地震反应。地震动输入为上文提到的5种加速度谱，输入方式为纵桥向+竖向，振型组合方法采用CQC(Complete Quadratic Combination)法，方向组合方法采用SRSS(Square Root of Sum of Square)法。表3，4给出了考虑前600阶振型贡献时在不同反应谱输入下桥梁墩柱关键截面内力、桥梁关键位移的对比关系。

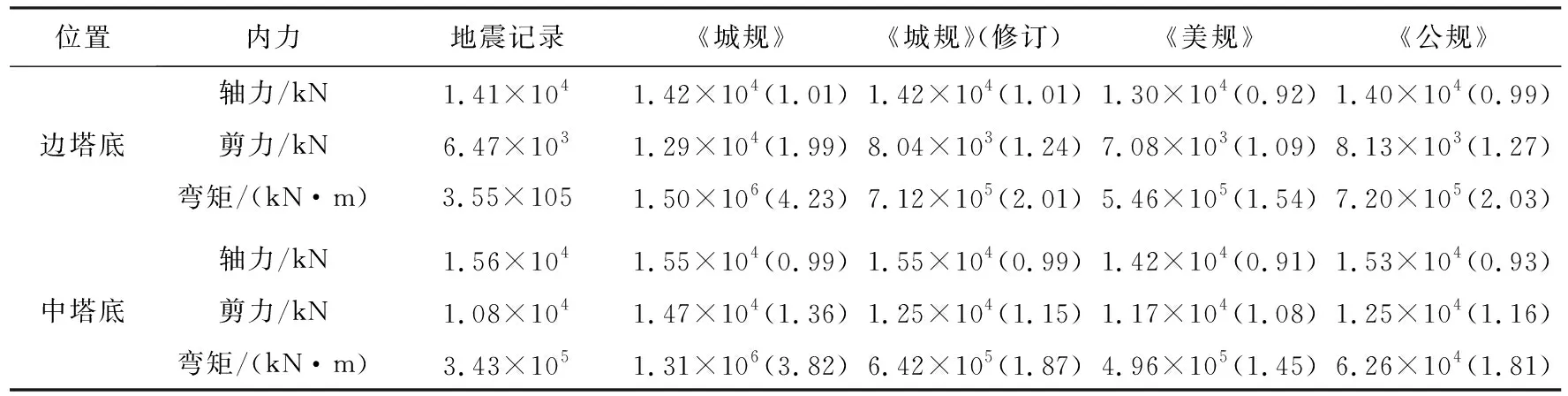
表3 不同反应谱输入下桥塔纵向地震内力

由表3可知，桥塔轴力在《城规》《公规》《美规》和《城规》(修订)反应谱输入下相差不大，与地震记录反应谱输入下的轴力相比误差均在10%之内，故轴力对加速度反应谱长周期分量不敏感；在不同反应谱输入下塔底弯矩差别较大，《城规》《公规》《城规》(修订)和《美规》输入下边塔的弯矩是地震记录反应谱输入下边塔弯矩的4.23，2.03，2.01，1.54倍，这说明纵桥向塔底弯矩对加速度反应谱长周期分量十分敏感。由表4可知，《城规》《公规》《城规》(修订)和《美规》反应谱输入下梁端位移是地震记录反应谱输入下梁端位移的4.26，2.00，2.03，1.57倍，说明加速度反应谱长周期分量对梁端纵向位移影响十分大。与地震记录反应谱输入下的结果相比，《城规》输入下塔底弯矩与主梁位移较大，说明对规范加速度反应谱超出周期范围部分取平台段，会造成纵向地震作用下塔底弯矩和主梁位移的几倍增加；对《城规》加速度反应谱长周期部分提出修正建议后，相比于《城规》输入下的反应，结构地震反应减少50%，但仍有足够的安全储备。

表4 不同反应谱输入下桥梁关键位移 m

为进一步验证加速度反应谱长周期分量对结构反应的影响，计算基本振型对结构地震响应的贡献。表5，6列出了仅考虑基本振型的结构反应及与考虑600阶振型结构反应的对比，表7列出了各反应谱基本周期所对应的谱值。

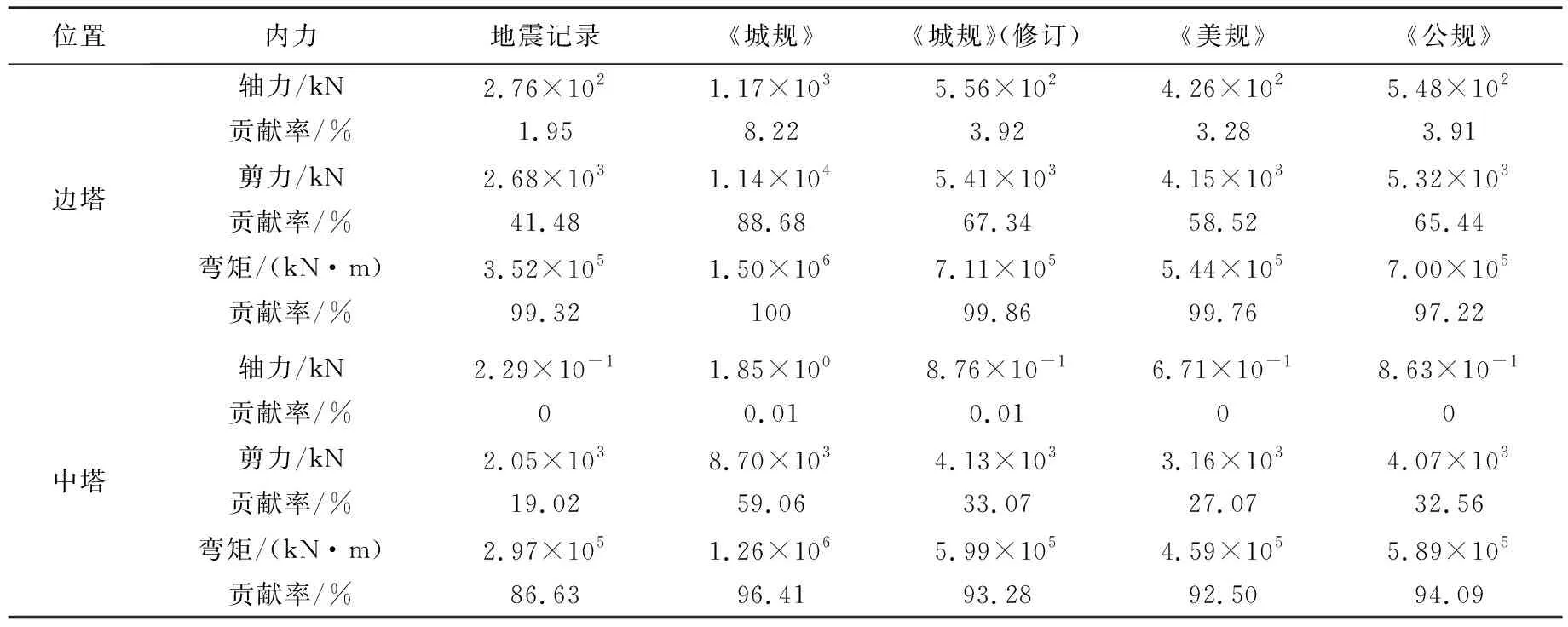
表5 基本振型对桥塔内力的贡献

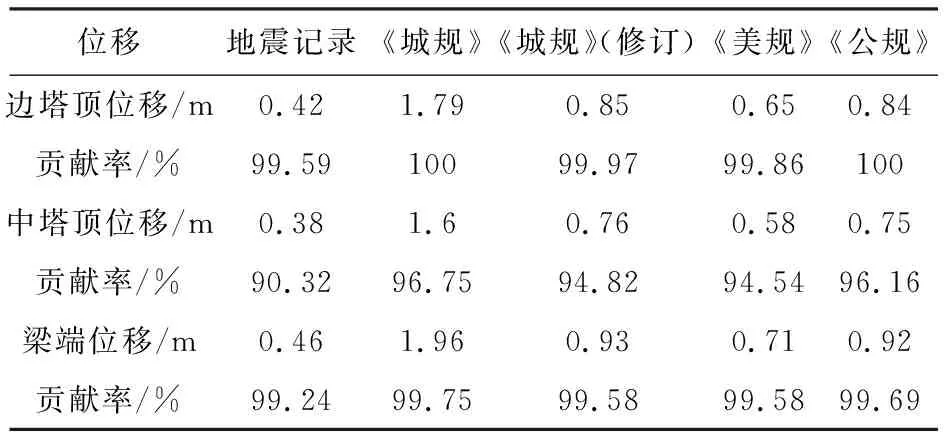
表6 基本振型对桥梁关键位移的贡献

表7 基本周期对应的反应谱谱值

由表5可知，在不同反应谱输入下，仅考虑基本振型桥塔的轴力占考虑600阶振型桥塔轴力的比例均在9%以内，说明基本振型对桥塔轴力贡献较小，也验证了轴力对加速度谱长周期分量不敏感；在不同反应谱输入下，仅考虑基本振型桥塔的弯矩占总弯矩的比例较大，均在85%以上。由表6可知，在不同反应谱输入下，由基本振型贡献的梁端位移占比均在99%以上。综上，加速度反应谱长周期分量会显著影响纵向地震输入下大跨度索支撑桥梁的桥塔弯矩与梁端位移。综合表5～7，不同反应谱输入下桥塔的弯矩与基本振型对应的不同加速度反应谱谱值分布规律一致；不同反应谱输入下梁端的位移与基本振型对应的不同位移反应谱谱值分布规律一致。故反应谱长周期段谱值规定不能过于保守，要符合实际地震动统计规律。

4 结 论

本文对比了中美桥梁抗震设计规范反应谱的长周期部分，并对《城规》反应谱长周期段提出了修正建议；以一座主跨为428 m的三塔自锚式悬索桥为例，分析反应谱长周期分量对桥梁结构不同地震反应分量的影响。得到以下结论：

(1)《城规》加速度反应谱6 s后如果拉平，对应的位移反应谱长周期段增长规律显著大于实际地震动位移谱统计规律，且周期越大，位移谱谱值相差越大。根据已有文献和7条实际地震动加速度反应谱均值，建议6 s后加速度反应谱按周期倒数的一次方关系衰减。

(2)对于漂浮体系大跨度索支撑桥梁，一阶纵飘振型对塔底纵向弯矩与梁端纵向位移贡献分别达85%与99%以上，可见加速度谱长周期分量显著影响结构墩柱弯矩与梁端位移。

(3)如果对《城规》设计反应谱超出周期范围部分取平台段，会造成纵向地震作用下塔底弯矩和主梁位移的几倍增加，按建议的周期倒数一次方关系衰减，可避免过度放大结构反应，但与地震记录输入下的反应相比仍具有一定的安全度。