双层高架桥框架式桥墩地震损伤试验

2021-11-10许成祥王粘锦

土木工程与管理学报 2021年5期

许成祥，王粘锦

(武汉科技大学城市建设学院，湖北武汉 430065)

作为交通中常见的桥型之一，双层高架桥梁能最大限度地减少土地占用面积，有效实现交通分流和扩容，是一种高效的交通网络解决方案，对工程投资的节省有着重要意义。20世纪50年代美国开启了修建双层高架桥梁的先例，并建设了多座双层高架桥梁[1]。

双层高架桥桥墩多采用框架式墩，桥墩的盖梁、立柱紧密连接，在遭受横向地震作用时，结构潜在的塑性铰区最多可达8个，其抗震性能不易满足要求，因此双层高架桥梁在地震中容易发生破坏，如1898年络马·普雷塔地震中，美国的Cypress双层高架桥在地震作用下二层桥面倒塌到一层桥面上而导致高架桥梁整体破坏。此后，很多学者开始对双层高架桥梁的抗震性能和地震损伤进行研究。Bollo等[2,3]通过实验和有限元模拟研究了地震作用下Cypress双层高架桥破坏的原因，研究表明墩柱的剪切破坏是引起桥梁倒塌的主要原因。Priestly等[4,5]对加固后的Cypress双层高架桥桥墩模型进行拟静力试验，结果表明加固方案是可行的，同时对加固方案进行优化。彭天波等[6,7]对上海市共和新路公铁两用双层高架桥进行拟动力试验，结果表明：结构的损伤主要发生在上、下立柱两端的潜在塑性铰区，盖梁和节点按能力保护设计而保持弹性，因此原结构采用能力设计原理进行抗震设计是合理的。张洁等[8]以洛塘河双层高架桥桥墩为原型，设计了两个配筋率不同的桥墩模型，研究墩柱配筋率对结构抗震性能的影响，结果表明高配筋率的墩柱模型节点和横梁破坏较严重，并用有限元分析验证了这一结论。杨宝林等[9]对洛塘河双层高架桥桥墩进行抗震性能试验，并对盖梁、立柱的设计提出了优化方案。魏晓龙等[10]对洛塘河双层高架桥进行有限元分析，以碰撞刚度等为参数，研究表明碰撞会导致节点处的立柱发生剪切破坏；孙玉顺[11]以“干式连接”和“湿式连接”两种不同的连接方式为参数对预制拼装钢管混凝土双柱墩的抗震性能进行研究，结果表明埋入式双柱墩的整体抗震性能要优于U型锚筋连接式的双柱墩，并采用有限元分析验证了这一结论；丁世广[12]通过对预制拼装式桥墩地震损伤及评估方法进行研究，结果明确了桥墩的4个性能水平，并基于Open-Sess数值模拟对桥墩试件损伤性能进行参数敏感性分析。耿波等[13]对地震作用下预制拼装桥墩的损伤演化过程与损伤状态进行研究，基与OpenSees数值模拟与试验结果对比，得到了预制拼装桥墩损伤指标计算公式。梁青峰[14]对双柱式桥墩进行有限元分析，研究表明，当桥墩轴压比取0.15，配筋率取1%时，桥墩的抗震性能最好，同时指出横系梁的设置会对桥梁抗剪产生不利影响。目前国内研究仅限于对山区双层高架桥和公铁两用桥梁的抗震性能研究，针对双层高架桥框架式桥墩地震损伤方面的研究较少。本文按立柱作为延性构件，盖梁和节点作为能力保护构件的桥梁抗震设计原则制作了缩尺比为1/5.5的双层高架桥框架式桥墩模型，并进行低周往复荷载作用的拟静力试验，分析桥墩的破坏特点、滞回特性、延性、耗能能力和刚度退化等。基于已有的地震损伤模型，定量描述在低周往复荷载作用下双层高架桥框架式桥墩的地震损伤演化过程。

1 试验概况

1.1 试件设计及制作

本试验桥墩原型按照现有规范进行设计[15,16]，原型桥墩混凝土强度等级为C30，上、下立柱截面尺寸均为1250 mm×1250 mm，上、下立柱高度均为7040 mm；上、下盖梁梁端均与立柱同宽，梁端截面尺寸为1250 mm×1540 mm，梁跨中截面尺寸为1250 mm×990 mm；上、下立柱配筋率均为1.2%，盖梁配筋率为1.1%。

文献[17]中提到钢筋混凝土试件拟静力试验的缩尺比例不宜小于1/10，考虑到实验室现场条件，试验模型按1/5.5的比例并进行等配筋率缩尺设计，缩尺后立柱截面尺寸为230 mm×230 mm，梁端截面尺寸为230 mm×280 mm，梁跨中截面尺寸为230 mm×180 mm，模型底座截面尺寸为1010 mm×500 mm，模型尺寸及配筋见图1[18]。

图1 桥墩模型尺寸及配筋/mm

桥墩模型混凝土强度等级为C30，立柱纵筋、盖梁纵筋均采用HRB400钢筋，立柱配筋率为1.19%。盖梁配筋率为1.14%；立柱、盖梁箍筋均采用HPB300钢筋，加密区间距为100 mm，非加密区间距为200 mm。在盖梁加腋处布置的吊筋、斜筋均采用HRB400钢筋。模型底座采用HRB400钢筋。

1.2 试件材料力学性能

试验同期实测同批次3个边长为150 mm×150 mm×150 mm的混凝土立方体抗压强度值，平均值见表1，钢筋力学性能实测值见表2。

表1 混凝土抗压强度实测值

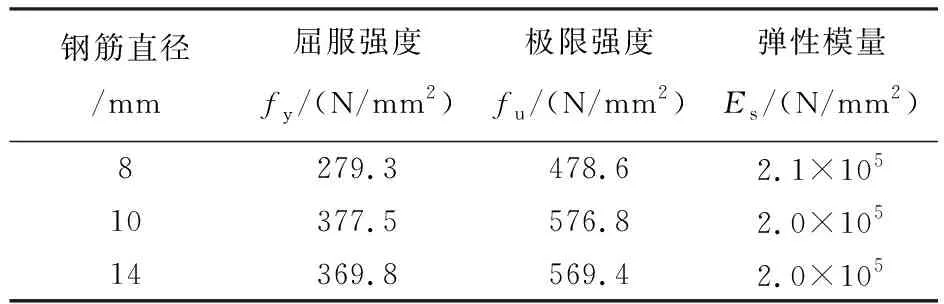
表2 钢筋力学性能实测值

1.3 加载装置及加载制度

桥墩模型采用8个高强螺栓通过地梁预留孔洞固定在地面上，水平荷载由行程为±150 mm的电液伺服作动器施加。竖向荷载采用自反力的加载方式，恒载值取桥墩上部结构自重，对原型桥墩上部结构自重进行等比例缩尺可得到每个千斤顶的数值，计算得到两个千斤顶施加荷载值为50 kN，加载装置和加载现场见图2。

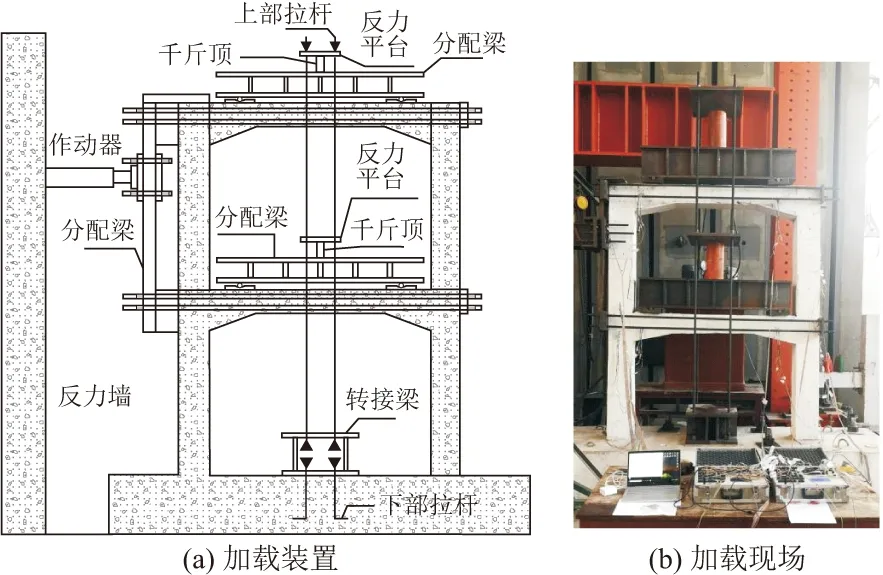
图2 加载装置和现场

水平荷载加载制度：水平荷载全程采用位移控制加载，桥墩屈服前按2.5 mm逐级递增，每级位移循环加载一次，桥墩屈服后，以屈服时加载点位移的倍数进行加载，每级加载循环三次，直至荷载下降到峰值荷载的85%以下停止加载[17]。考虑到实验室现场条件，由于只有一个水平作动器，采用外挂分配梁的加载方式对上、下层按比例2∶1分级加载。水平加载制度如图3。

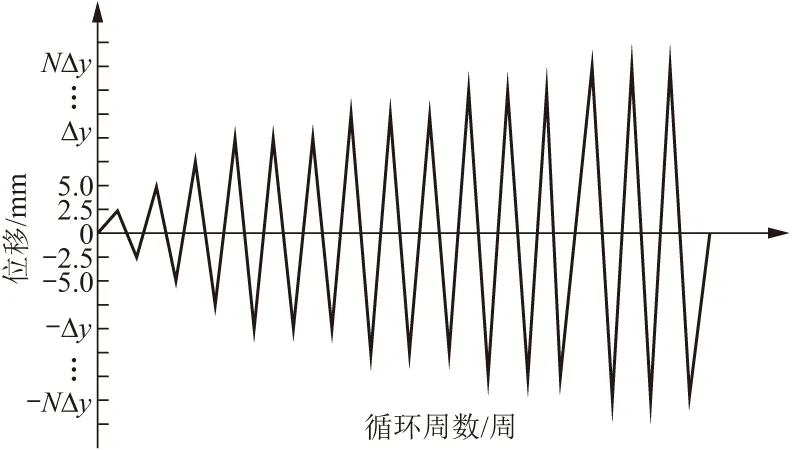
图3 水平加载制度

1.4 测点布置

双层高架桥框架式桥墩在遭受地震作用时，损伤部位主要发生在桥墩潜在塑性铰区，因此在桥墩潜在塑性铰区的钢筋上布置应变片。测点点位布置如图4所示。

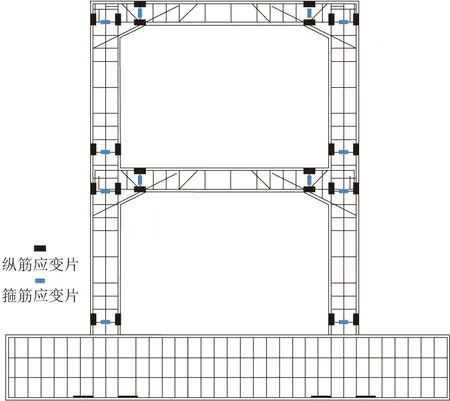
图4 钢筋应变片测点点位位置

2 桥墩损伤过程

在整个试验过程中，以作动器施加推力为正，施加拉力为负。

在水平位移为±5 mm循环加载过程中，LZ1，LZ3柱底均开始出现裂缝，在水平位移为±12.5 mm之前，LZ4柱顶出现交叉斜裂缝，GL1，GL2梁底均出现裂缝，但这些裂缝长度较短，宽度很小，卸载后均可闭合。应变监测系统显示钢筋应变较小均没有达到屈服应变，桥墩强度刚度退化不明显，以弹性变形为主，此时桥墩处于无损伤阶段。

在水平位移为±18 mm循环加载过程中，LZ4柱顶有新裂缝产生且原有裂缝继续发展并贯通，LZ1，LZ3柱底原有裂缝贯通并有新裂缝产生，应变监测系统显示LZ1柱底一条纵筋应变超出屈服应变，盖梁并没有出现大的变形，盖梁纵筋大部分处于弹性工作阶段，此时桥墩处于损伤初始阶段。

在水平位移为±36 mm第二个循环加载过程中，GL1梁底左端出现两条新裂缝，原有裂缝贯穿，LZ1柱底原有裂缝宽度增大，混凝土保护层开始剥落，并伴随有新裂缝产生，此时LZ1柱底开始形成塑性铰，应变监测系统显示桥墩立柱多数纵向钢筋已经超出屈服应变。在水平位移为±54 mm第二个循环加载过程中，LZ4柱顶混凝土保护层剥落，箍筋裸露在外且伴随有新裂缝产生，第二个循环加载过程中JD3处立柱柱顶混凝土保护层剥落，纵筋裸露在外。在水平位移为±63 mm第一个循环加载过程中，LZ3柱底混凝土保护层剥落，一条纵筋裸露在外。第二个循环加载过程中，LZ1柱底混凝土严重剥落，三条纵筋裸露在外，塑性铰已经形成，其中一根钢筋被压弯，同级位移继续加载，可听到混凝土掉落的声音，观察发现LZ2柱顶混凝土剥落且较为严重，此时桥墩处于损伤稳定增长阶段。

伴随着水平位移继续增大，桥墩整体变形加快但荷载开始慢慢降低。在水平位移为±72 mm第一个循环加载过程中，桥墩模型的水平承载力已经开始下降，但下降较为缓慢；在第三个循环加载时水平承载力明显下降，此时桥墩处于损伤急剧发展阶段，当水平位移为±90 mm第一个循环加载过程中，水平荷载低于峰值荷载的85%时停止试验。此时可以看到，LZ1，LZ3柱底混凝土剥落，纵向钢筋及箍筋外露，LZ1一条纵向钢筋被压弯，LZ2，LZ4柱顶混凝土剥落严重，梁、柱纵筋外露，柱箍筋外露；柱端及梁、柱交接位置的混凝土剥落严重，GL1梁底仅有少量混凝土剥落，GL2梁底有多条贯穿裂缝，混凝土并没有剥落，节点损伤较轻，承载力没有显著降低；由此可以看出，桥墩模型在整个试验过程中经历了开裂、屈服、峰值和极限四个阶段。桥墩的破坏形态如图5。

图5 桥墩破坏现象

通过观察分析整个试验中桥墩破坏过程并参考桥梁抗震设计目标可知：

(1)从立柱的破坏状态看出，桥墩的塑性铰主要出现在LZ1，LZ3柱底和柱顶，塑性铰区域分布合理，立柱延性得到了充分发挥，桥墩设计满足立柱作为延性构件的抗震设计原则。

(2)从盖梁和节点的破坏状态看出，GL1梁底出现少量混凝土剥落，GL2梁底仅出现多条裂缝，混凝土基本未剥落，盖梁总体破坏较轻；节点区域均发生了一定程度的损伤，但损伤并不严重，符合盖梁和节点作为能力保护构件的抗震设计原则。

3 试验结果分析

3.1 滞回曲线

滞回曲线是结构抗震性能分析的基础，由试验测得的滞回曲线如图6。

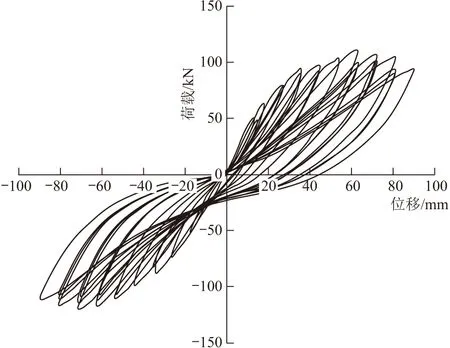
图6 滞回曲线

从图6可以看出：加载初期，水平力很小，未达到混凝土的开裂荷载，滞回曲线近似于直线发展，此时桥墩基本处于弹性工作阶段。随着水平位移的逐级增加，LZ1，LZ3柱底开始出现裂缝并逐渐增加，此时可以看出滞回曲线斜率逐渐变小，滞回环由直线向曲线过渡并向位移轴倾斜，卸载后的残余应变不可忽略，水平位移逐渐增大的同时桥墩的整体变形也在增加，说明桥墩的整体刚度在退化，此时桥墩由线性工作阶段转向非线性工作阶段。随着水平位移进一步增加，钢筋混凝土之间粘结作用不断退化且产生滑移，混凝土裂缝在卸载后也不能完全闭合，混凝土裂缝扩展较宽且混凝土剥落，滞回曲线发生明显的捏缩现象，承载力和刚度退化严重。

3.2 骨架曲线

骨架曲线是滞回曲线上每级循环的荷载-位移曲线达到最大峰值的轨迹，是确定恢复力模型特征点的重要依据，结构的骨架曲线见图7。

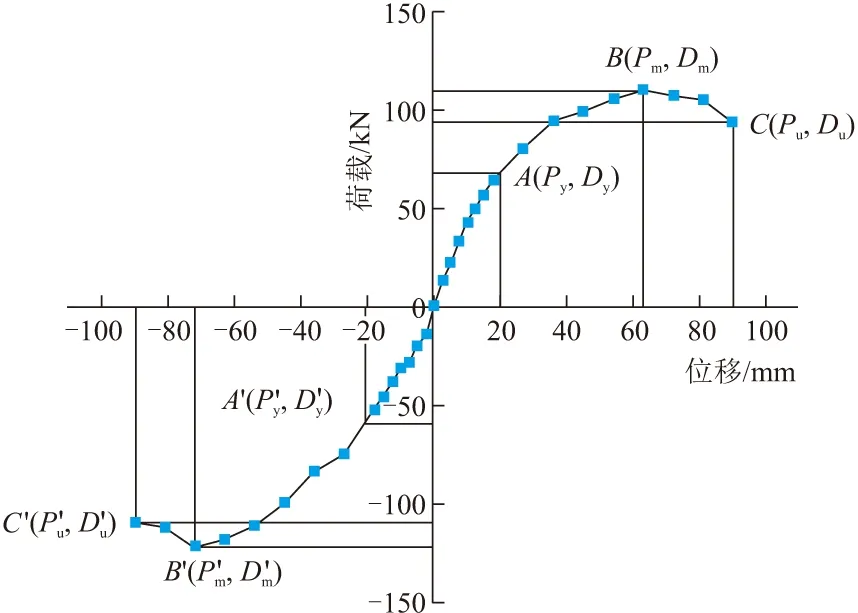
图7 骨架曲线

从图7可以看出：在加载初期，荷载和位移基本呈线性变化关系，表明此阶段桥墩基本处于弹性工作状态，卸载时构件可回到原来的位置，残余应变可忽略不计。在桥墩达到极限承载力之前，荷载随着位移的逐级增加而增加，且荷载增速大于位移增速。在桥墩达到极限承载力之后，LZ1，LZ3柱底已经形成塑性铰，随着位移的增加，桥墩整体的强度、刚度退化严重，承载力也开始下降，从骨架曲线中可以看出承载力下降段并不陡峭，较为平缓，说明桥墩在破坏之前仍具有较好的延性和耗能能力。由骨架曲线可知，正、反向加载得到的骨架曲线不对称，同位移时刻桥墩的正向承载力大于反向承载力，这是由于桥墩在受到相反方向的推、拉力时盖梁处于不同的受力状态所导致的。

骨架曲线中，可用初始刚度Ke、硬化刚度Ks和负刚度Kn来表示桥墩不同阶段的刚度。其中Ke用来描述桥墩的弹性阶段，为曲线上OA的连线；Ks用来描述桥墩屈服后的受拉刚化效应，为曲线上AB的连线；Kn用来描述桥墩达到峰值荷载后承载力衰减的幅度，为曲线上BC的连线。硬化刚度和负刚度均与初始刚度成比例，即：

Ks=αsKe

(1)

Kn=αnKe

(2)

式中：αs，αn分别为硬化刚度和负刚度与初始刚度的比例系数，通过骨架曲线确定。

本试验由式(1)(2)确定了桥墩的αs=0.23，αn=-0.17，文献[19]中提到，对于钢结构αs=0.03，αn=-0.03，对于普通钢筋混凝土结构αs=0.1，αn=-0.24。桥墩的αs均高于钢结构和普通钢筋混凝土结构，这说明当桥墩屈服后其强度仍可以有较大程度的提升，桥墩的αn介于二者之间，说明其达到极限承载力后的性能要优于普通钢筋混凝土结构而低于钢结构。

3.3 桥墩破坏机制

图8为桥墩不同加载方向下塑性铰出现的位置和顺序，由图可知，无论是正向加载还是反向加载，均是柱端先出现塑性铰，梁端后出现塑性铰，且基本上柱端铰出现之后，梁端才出现铰，这体现了桥墩模型属于柱铰破坏机制，且桥墩破坏是由柱端塑性铰引起的。在桥梁抗震设计规范中，为了避免桥梁发生倒塌，盖梁和节点宜作为能力保护构件进行设计，立柱适合作为延性构件进行设计，因此桥墩最终的破坏为柱铰破坏机制，桥墩立柱损伤大于盖梁和节点损伤。

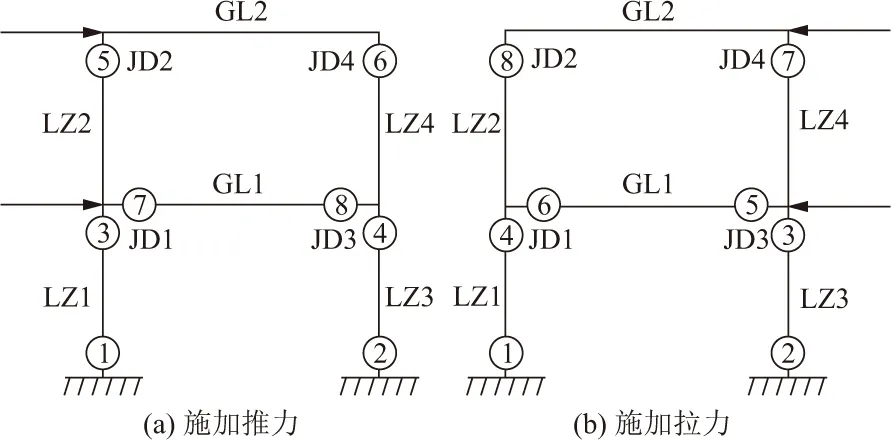
图8 不同向荷载下桥墩塑性铰出现的位置和顺序

图9给出了桥墩各节点处梁端弯矩值Mb，柱端弯矩值Mc，由图可知，梁端受弯承载力(50.7 kN·m)大于柱端受弯承载力(21.3 kN·m)，由试验知立柱的损伤程度大于盖梁，与试验结果基本吻合。通过观察分析整个试验过程，桥墩立柱损伤早于盖梁损伤，立柱损伤程度大于盖梁损伤程度，桥墩一层损伤程度大于二层损伤程度。节点在前期仅出现多条裂缝，后期出现少量混凝土剥落，当桥墩接近破坏荷载时，立柱损伤严重，盖梁和节点损伤较轻。

图9 桥墩盖梁、立柱受弯承载力/( kN·m)

3.4 延性性能

延性是体现结构抗震性能的重要指标之一，延性大的结构在进入破坏阶段的过程中，承载能力不会随着位移的增加而有明显下降，塑性变形能力很强。延性系数μ的计算公式为：

μ=Δu/Δy

(3)

式中：Δu，Δy分别为破坏位移和屈服位移。

本文中屈服位移取骨架曲线弹性阶段的延长线与过峰值点的切线交点处的位移值[20]。破坏位移取荷载下降至最大荷载85%时对应的位移。延性系数见表3。

表3 桥墩延性系数

由表3可知：桥墩的延性系数为4.35，达到了钢筋混凝土框架结构系数大于4的要求，说明双层高架桥框架式桥墩设计满足延性要求。桥墩结构特征点相关荷载和位移见表4。

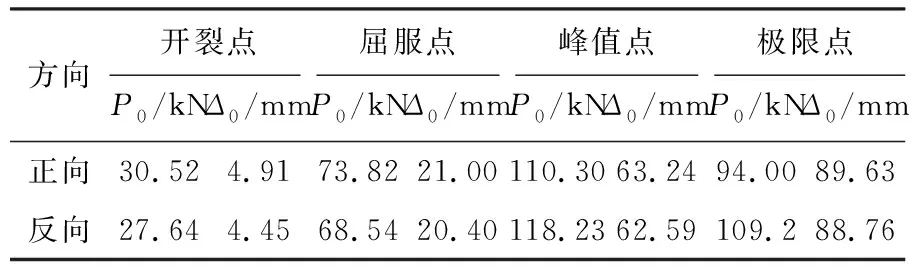
表4 桥墩结构特征点相关荷载和位移

3.5 承载力退化

承载力退化反映了结构的累积损伤，是结构抗震性能的重要指标。为了反映出构件的承载力退化，引入承载力退化系数λi，其公式为：

λi=Pi/Pmax

(4)

式中：λi为第i次加载循环时的承载力退化系数；Pi为第i次加载循环时对应的峰值荷载；Pmax为加载过程中所得最大峰值点荷载。试验所得承载力退化曲线如图10所示。

从曲线中可以看出：从整个试验过程来看，桥墩的承载力退化系数呈下降趋势，主要是由于桥墩的累计损伤所导致，主要体现在桥墩立柱柱底塑性铰的不断发展。前期承载力退化系数先增后减是由于桥墩未屈服承载力上升的缘故。在桥墩进入弹塑性阶段后承载力开始退化，但退化并不明显，在桥墩进入破坏阶段后，承载力退化速率开始加快，说明桥墩在破坏前具有较好的延性性能。

3.6 刚度退化

结构的刚度随着加、卸载循环次数的增加而降低的特性称为刚度退化。刚度退化是通过试件在不同位移延性系数时割线刚度Ki来表示，其计算公式为：

(5)

式中：+Fi，-Fi为第i次循环正、反向加载时对应的峰值点荷载；+Δi，-Δi为第i次循环正、反向加载时对应的峰值点位移。刚度退化曲线如图11所示。

由图11可以看出，在整个试验过程中，桥墩的割线刚度随着水平位移的增加而逐渐减小，曲线斜率在前期较为陡峭，随着位移的增加斜率逐渐放缓，退化规律相近，这是由于桥墩立柱开始形成塑性铰，且塑性铰发展较为缓慢。在试验加载后期桥墩刚度较小，但仍具有承受一定荷载的能力，这体现了其具有较好的抗震能力，可以防止在地震作用下发生突然坍塌。

3.7 耗能比

耗能比是反映构件在地震作用下能量耗散能力的一个重要指标，耗能比大的结构在遭遇地震作用时抵御累积损伤的能力越强，受到的地震损伤越小。计算示意图如图12所示，耗能比ζ的计算公式为：

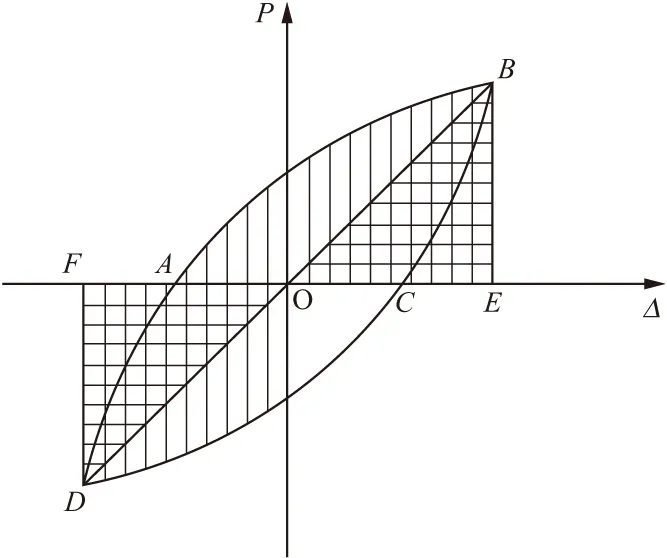
图12 耗能比计算示意

ζ=A1/A

(6)

式中：A=A1+A2，为水平力做的功，其中A1，A2分别为构件在荷载加卸载循环一次所吸收和释放的能量(A1为曲边形ABC的面积，A2为曲边形BEC的面积)。

由双层高架桥框架式桥墩的滞回曲线计算得到桥墩的耗能比，数值见表5，由表5可以看出桥墩屈服时的耗能比略小于钢管混凝土框架结构(钢管混凝土框架结构的耗能比在0.26～0.36之间)，这表明了此桥墩具有较好的耗能能力和抗震性能[21]。

表5 桥墩结构的耗能比

4 累积损伤分析

结构在低周往复荷载作用下会发生累积损伤，当损伤累积到一定程度后，结构将无法承受荷载而发生破坏。结构的损伤程度一般用损伤指数D表示，损伤指数是一个很直观的变量，能直接反映结构或构件的破坏程度且与结构的能量、变形、强度三者之间均存在关系，能够较全面地反映结构的性能，它体现如何将结构的性能目标转变成具体的数值。当D=0时，表示结构无损伤，当D=1时，表示结构安全破坏，当D的值处于(0,1)之间时，表示结构的状态处于无损与完全破坏之间。损伤指数D是单调递增函数，即损伤指数朝着增大的方向发展，且损伤是不可逆的过程。袁坤[22]提出了基于滞回耗能和能量耗散的损伤模型，该模型可以计算出加载过程中任意循环结构的累积损伤指数。图13给出了循环加载过程中桥墩各主要阶段的损伤指数。

图13 循环加载过程中桥墩各主要阶段的损伤指数

从图13可以看出，随着荷载循环次数的增加，桥墩的累积损伤逐渐增大，同级位移循环加载中，后一级循环桥墩的损伤指数大于前一级，说明相同变形时，循环次数的增加会导致累积损伤的增加。

桥墩开裂点的损伤指数为0.22，此时只有LZ1，LZ3柱底出现裂缝，且裂缝宽度较小，卸载时可闭合，桥墩处于弹性工作阶段。桥墩屈服点的损伤指数为0.35～0.41，此时LZ1一条纵筋已经屈服，柱底原有裂缝已经贯通且有新裂缝产生，GL1梁底出现裂缝。桥墩峰值点的损伤指数为0.65～0.70，此时桥墩承载力达到峰值，LZ1，LZ3柱底均有混凝土剥落，且LZ1剥落现象较为明显，GL1，GL2梁底均出现多条贯穿裂缝。桥墩破坏点的损伤指数为0.82，此时LZ1柱底混凝土剥落严重，三条纵筋裸露在外，其中一根钢筋被压弯，GL1梁底左端出现少量混凝土剥落，盖梁节点损伤较轻，柱端塑性铰充分发挥了作用，卸载后桥墩整体发生倾斜，不能恢复到原来的位置，但并没有发生倒塌，说明桥墩具有很好的抗震性能及抵御累积损伤的能力。